【人教九上数学学霸听课笔记】24.1.1 圆 课件(共41张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】24.1.1 圆 课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 21:36:47 | ||
图片预览







文档简介
(共41张PPT)
24.1 圆的有关性质
第二十四章
圆
24.1.1 圆
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
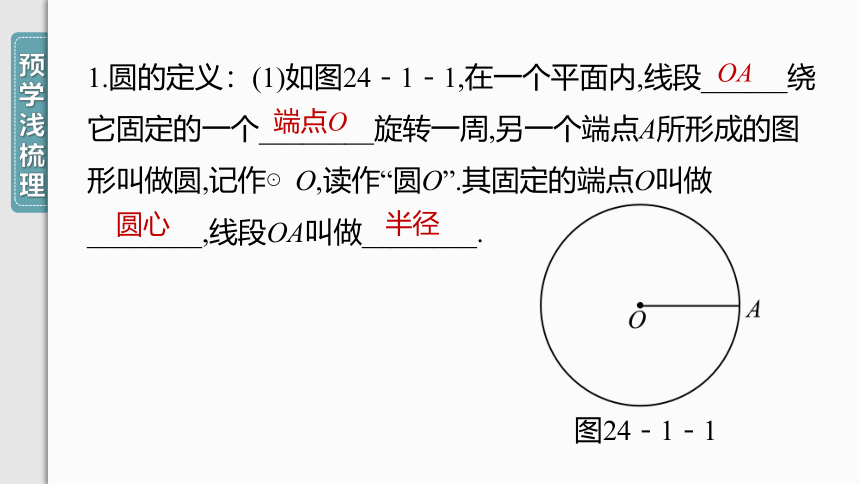
1.圆的定义:(1)如图24-1-1,在一个平面内,线段______绕
它固定的一个________旋转一周,另一个端点A所形成的图
形叫做圆,记作⊙O,读作“圆O”.其固定的端点O叫做
________,线段OA叫做________.
图24-1-1
OA
端点O
圆心
半径
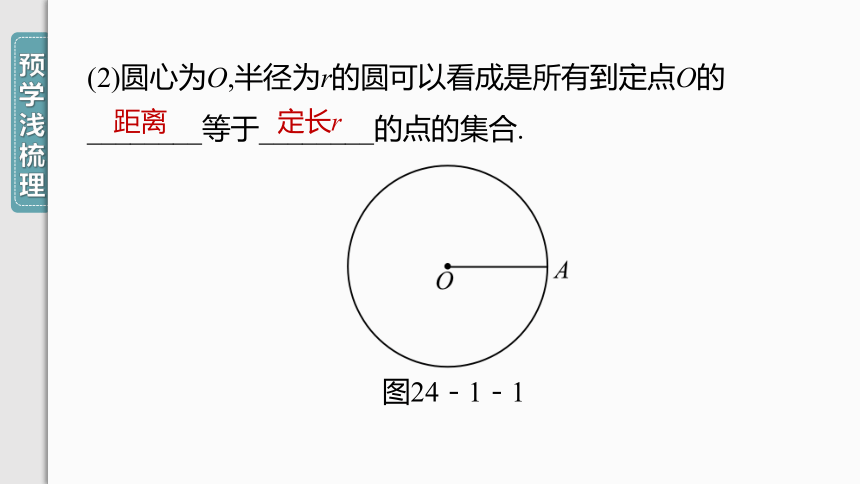
(2)圆心为O,半径为r的圆可以看成是所有到定点O的
________等于________的点的集合.
图24-1-1
距离
定长r
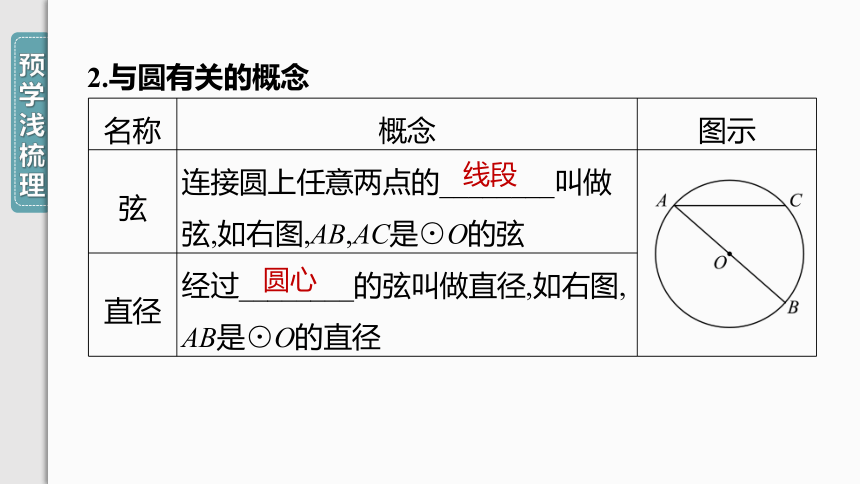
2.与圆有关的概念
名称 概念 图示
弦 连接圆上任意两点的________叫做弦,如右图,AB,AC是⊙O的弦
直径 经过________的弦叫做直径,如右图, AB是⊙O的直径
线段
圆心
部分
直径
小于
大于
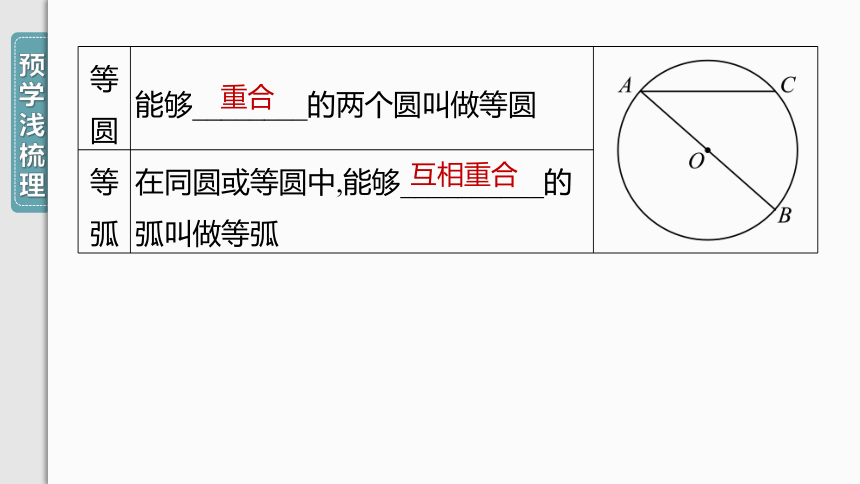
等圆 能够________的两个圆叫做等圆
等弧 在同圆或等圆中,能够__________的弧叫做等弧
重合
互相重合
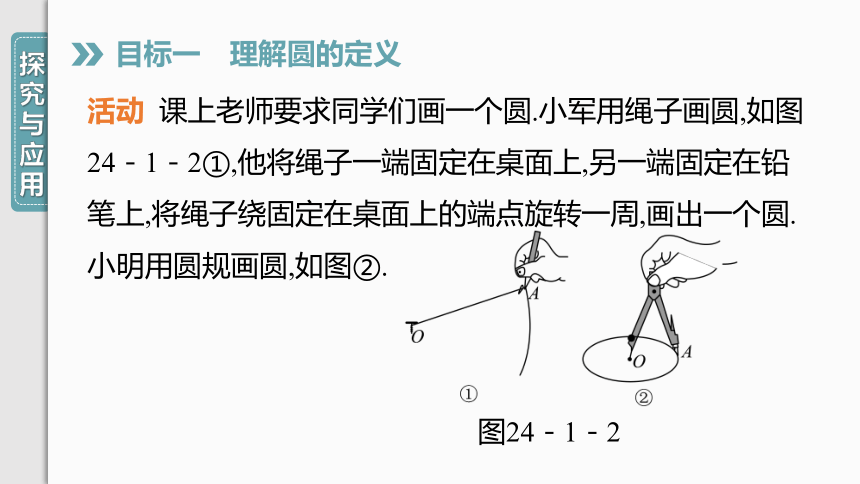
目标一 理解圆的定义
活动 课上老师要求同学们画一个圆.小军用绳子画圆,如图24-1-2①,他将绳子一端固定在桌面上,另一端固定在铅笔上,将绳子绕固定在桌面上的端点旋转一周,画出一个圆.小明用圆规画圆,如图②.
图24-1-2
(1)小军与小明在画圆的过程中,他们固定了几个点 是哪个点
解:他们固定了一个点,是点O.
(2)在画圆的过程中,转动的另一点A到固定点O的距离始终相等吗
解:相等.
(3)根据画圆的过程,请你尝试给出圆的定义.
解:定义:在一个平面内,一条线段绕它固定的一个端点旋转一周,另一个端点所形成的图形叫做圆.
圆定义的静态解读
1.圆上各点到定点的距离都等于定长;
2.到定点的距离等于定长的点都在同一个圆上.
因此,圆可以看成是所有到________的距离等于________的
点的集合.
归纳总结
定点
定长
例1 以点O为圆心画圆,可以作________个圆( )
A.1 B.2
C.3 D.无数
D
例 体育课上,体育老师让全班50名同学沿着界线站成一排做套圈游戏,如图J24-1-1,你认为老师这样设计游戏公平吗 若公平,请说明理由;若不公平,你认为怎样设计才能使游戏公平呢
解:不公平.
公平的设计方案:50名同学围成一个
以目标为圆心的圆.
图J24-1-1
例2 [教材P80例1]矩形ABCD的对角线AC,BD相交于点O.求证:A,B,C,D四个点在以点O为圆心的同一个圆上.
证明:∵四边形ABCD为矩形,
∴OA=OC=OB=OD,
∴A,B,C,D四个点在以点O为圆心,OA为半径的圆上(如图).
变式 将教材例1中的矩形改为如图24-1-3所示的四边形ABCD,其中∠A=∠C=90°,此时点A,B,C,D仍在同一个圆上吗 为什么
图24-1-3
解:点A,B,C,D仍在同一个圆上.
理由如下:
如图,连接BD,取BD的中点O,连接OA,OC.
∵O是Rt△ABD的斜边BD的中点,
∴OA=OB=OD.
同理,OC=OB=OD,
∴OA=OB=OC=OD,
∴点A,B,C,D在以BD的中点O为圆心,OA为半径的圆上.
证明多个点共圆的方法
说明多个点到某定点的距离相等 这多个点在同一个圆上.
方法感悟
目标二 理解圆的有关概念
例3 有下列说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④长度相等的弧是等弧.其中错误的有
( )
A.1个 B.2个
C.3个 D.4个
C
[解析] 根据圆、直径、弦等的概念来判断.半径确定了,只能说明圆的大小确定了,但是圆的位置没有确定.直径是弦,但弦不一定是直径.等弧的定义包括两方面的内容:长度和所在圆的半径都相等.所以①③④的说法是错误的.
归纳
圆中容易混淆的“两组概念”
1.弦与直径:
(1)直径是圆中最长的弦,但弦不一定是直径;
(2)弦是连接圆上任意两点的线段,而直径是经过圆心的弦.
归纳
2.弧与半圆:
(1)半圆是弧,但弧不一定是半圆;
(2)圆上任意两点分圆成两条弧,圆的任意一条直径的两个端
点把圆分成两条弧,每一条弧都叫做半圆.
拓展 如图24-1-4所示,已知CD是⊙O的直径,∠EOD=78°,点A在DC的延长线上,AE交⊙O于点B,且AB=OC,求∠A的度数.
[解析] 已知∠EOD=78°,与∠A构成
外角的关系,而∠E的度数也未知,且
AB=OC这一条件不能直接使用,因此
想到同圆的半径相等,需作半径OB,
从而得到OB=AB.
图24-1-4
解:如图,连接OB.
∵AB=OC,OB=OC,
∴AB=OB,∴∠A=∠1.
又∵OB=OE,
∴∠E=∠2=∠1+∠A=2∠A,
∴∠EOD=∠E+∠A=3∠A.
又∵∠EOD=78°,∴3∠A=78°,
∴∠A=26°.
圆中常添辅助线—— 作半径
作半径构造等腰三角形是解决有关圆问题的常用方法.
方法总结
解:(1)如图①②所示.
(2)①若点B,C在直线OA的异侧,连接OA,OB,OC,如图③.
∵AC=OA=OC=5,∴△OAC是等边三角形,∴∠OAC=60°.
∴OA2+OB2=AB2,
∴△OAB是直角三角形,且∠AOB=90°.
又∵OA=OB,∴∠OAB=45°,
∴∠BAC=∠OAB+∠OAC=45°+60°=105°.
②若点B,C在直线OA的同侧,连接OA,OB,OC,如图④.
同①可得∠OAC=60°,∠OAB=45°,
则∠BAC=∠OAC-∠OAB=60°-45°=15°.
综上,∠BAC的度数是105°或15°.
圆中常见的三种特殊的弦
如图J24-1-2,设⊙O的半径为r.
(1)如图①,若AB=r,则∠AOB=60°;
方法总结
图J24-1-2
图J24-1-2
1.有下列说法:①直径是弦;②弦是直径;③半圆是弧;④弧是半圆.其中正确的说法是( )
A.①②③④ B.①③
C.②④ D.①④
B
[解析] 因为弦不一定经过圆心,所以弦不一定是直径,所以说法②是错误的;因为连接弧的两个端点的线段不一定经过圆心,所以弧不一定是半圆,所以说法④是错误的.
2.如图24-1-5,________是⊙O的直径;__________是⊙O的弦;__________是劣弧;__________是优弧.
[解析] 根据弦、优弧、劣弧的定义填空.
图24-1-5
AC
AB,BC,AC
3.⊙O的半径为3 cm,则⊙O中最长的弦的长度为________.
6 cm
4.如图24-1-6,在⊙O中,弦AC∥半径OB,∠BOC=50°,求∠C,∠AOC,∠OAB的度数.
图24-1-6
∠C=50°,∠AOC=80°,∠OAB=25°
5.已知:如图24-1-7,AB是⊙O的弦,点C,D在AB上,AC=BD,连接OC,OD.求证:OC=OD.
证明:连接OA,OB.
∵OA=OB,∴∠A=∠B.
又∵AC=BD,
∴△OAC≌△OBD(SAS),∴OC=OD.
图24-1-7
https://www.21cnjy.com/help/help_extract.php
24.1 圆的有关性质
第二十四章
圆
24.1.1 圆
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
1.圆的定义:(1)如图24-1-1,在一个平面内,线段______绕
它固定的一个________旋转一周,另一个端点A所形成的图
形叫做圆,记作⊙O,读作“圆O”.其固定的端点O叫做
________,线段OA叫做________.
图24-1-1
OA
端点O
圆心
半径
(2)圆心为O,半径为r的圆可以看成是所有到定点O的
________等于________的点的集合.
图24-1-1
距离
定长r
2.与圆有关的概念
名称 概念 图示
弦 连接圆上任意两点的________叫做弦,如右图,AB,AC是⊙O的弦
直径 经过________的弦叫做直径,如右图, AB是⊙O的直径
线段
圆心
部分
直径
小于
大于
等圆 能够________的两个圆叫做等圆
等弧 在同圆或等圆中,能够__________的弧叫做等弧
重合
互相重合
目标一 理解圆的定义
活动 课上老师要求同学们画一个圆.小军用绳子画圆,如图24-1-2①,他将绳子一端固定在桌面上,另一端固定在铅笔上,将绳子绕固定在桌面上的端点旋转一周,画出一个圆.小明用圆规画圆,如图②.
图24-1-2
(1)小军与小明在画圆的过程中,他们固定了几个点 是哪个点
解:他们固定了一个点,是点O.
(2)在画圆的过程中,转动的另一点A到固定点O的距离始终相等吗
解:相等.
(3)根据画圆的过程,请你尝试给出圆的定义.
解:定义:在一个平面内,一条线段绕它固定的一个端点旋转一周,另一个端点所形成的图形叫做圆.
圆定义的静态解读
1.圆上各点到定点的距离都等于定长;
2.到定点的距离等于定长的点都在同一个圆上.
因此,圆可以看成是所有到________的距离等于________的
点的集合.
归纳总结
定点
定长
例1 以点O为圆心画圆,可以作________个圆( )
A.1 B.2
C.3 D.无数
D
例 体育课上,体育老师让全班50名同学沿着界线站成一排做套圈游戏,如图J24-1-1,你认为老师这样设计游戏公平吗 若公平,请说明理由;若不公平,你认为怎样设计才能使游戏公平呢
解:不公平.
公平的设计方案:50名同学围成一个
以目标为圆心的圆.
图J24-1-1
例2 [教材P80例1]矩形ABCD的对角线AC,BD相交于点O.求证:A,B,C,D四个点在以点O为圆心的同一个圆上.
证明:∵四边形ABCD为矩形,
∴OA=OC=OB=OD,
∴A,B,C,D四个点在以点O为圆心,OA为半径的圆上(如图).
变式 将教材例1中的矩形改为如图24-1-3所示的四边形ABCD,其中∠A=∠C=90°,此时点A,B,C,D仍在同一个圆上吗 为什么
图24-1-3
解:点A,B,C,D仍在同一个圆上.
理由如下:
如图,连接BD,取BD的中点O,连接OA,OC.
∵O是Rt△ABD的斜边BD的中点,
∴OA=OB=OD.
同理,OC=OB=OD,
∴OA=OB=OC=OD,
∴点A,B,C,D在以BD的中点O为圆心,OA为半径的圆上.
证明多个点共圆的方法
说明多个点到某定点的距离相等 这多个点在同一个圆上.
方法感悟
目标二 理解圆的有关概念
例3 有下列说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④长度相等的弧是等弧.其中错误的有
( )
A.1个 B.2个
C.3个 D.4个
C
[解析] 根据圆、直径、弦等的概念来判断.半径确定了,只能说明圆的大小确定了,但是圆的位置没有确定.直径是弦,但弦不一定是直径.等弧的定义包括两方面的内容:长度和所在圆的半径都相等.所以①③④的说法是错误的.
归纳
圆中容易混淆的“两组概念”
1.弦与直径:
(1)直径是圆中最长的弦,但弦不一定是直径;
(2)弦是连接圆上任意两点的线段,而直径是经过圆心的弦.
归纳
2.弧与半圆:
(1)半圆是弧,但弧不一定是半圆;
(2)圆上任意两点分圆成两条弧,圆的任意一条直径的两个端
点把圆分成两条弧,每一条弧都叫做半圆.
拓展 如图24-1-4所示,已知CD是⊙O的直径,∠EOD=78°,点A在DC的延长线上,AE交⊙O于点B,且AB=OC,求∠A的度数.
[解析] 已知∠EOD=78°,与∠A构成
外角的关系,而∠E的度数也未知,且
AB=OC这一条件不能直接使用,因此
想到同圆的半径相等,需作半径OB,
从而得到OB=AB.
图24-1-4
解:如图,连接OB.
∵AB=OC,OB=OC,
∴AB=OB,∴∠A=∠1.
又∵OB=OE,
∴∠E=∠2=∠1+∠A=2∠A,
∴∠EOD=∠E+∠A=3∠A.
又∵∠EOD=78°,∴3∠A=78°,
∴∠A=26°.
圆中常添辅助线—— 作半径
作半径构造等腰三角形是解决有关圆问题的常用方法.
方法总结
解:(1)如图①②所示.
(2)①若点B,C在直线OA的异侧,连接OA,OB,OC,如图③.
∵AC=OA=OC=5,∴△OAC是等边三角形,∴∠OAC=60°.
∴OA2+OB2=AB2,
∴△OAB是直角三角形,且∠AOB=90°.
又∵OA=OB,∴∠OAB=45°,
∴∠BAC=∠OAB+∠OAC=45°+60°=105°.
②若点B,C在直线OA的同侧,连接OA,OB,OC,如图④.
同①可得∠OAC=60°,∠OAB=45°,
则∠BAC=∠OAC-∠OAB=60°-45°=15°.
综上,∠BAC的度数是105°或15°.
圆中常见的三种特殊的弦
如图J24-1-2,设⊙O的半径为r.
(1)如图①,若AB=r,则∠AOB=60°;
方法总结
图J24-1-2
图J24-1-2
1.有下列说法:①直径是弦;②弦是直径;③半圆是弧;④弧是半圆.其中正确的说法是( )
A.①②③④ B.①③
C.②④ D.①④
B
[解析] 因为弦不一定经过圆心,所以弦不一定是直径,所以说法②是错误的;因为连接弧的两个端点的线段不一定经过圆心,所以弧不一定是半圆,所以说法④是错误的.
2.如图24-1-5,________是⊙O的直径;__________是⊙O的弦;__________是劣弧;__________是优弧.
[解析] 根据弦、优弧、劣弧的定义填空.
图24-1-5
AC
AB,BC,AC
3.⊙O的半径为3 cm,则⊙O中最长的弦的长度为________.
6 cm
4.如图24-1-6,在⊙O中,弦AC∥半径OB,∠BOC=50°,求∠C,∠AOC,∠OAB的度数.
图24-1-6
∠C=50°,∠AOC=80°,∠OAB=25°
5.已知:如图24-1-7,AB是⊙O的弦,点C,D在AB上,AC=BD,连接OC,OD.求证:OC=OD.
证明:连接OA,OB.
∵OA=OB,∴∠A=∠B.
又∵AC=BD,
∴△OAC≌△OBD(SAS),∴OC=OD.
图24-1-7
https://www.21cnjy.com/help/help_extract.php
同课章节目录
