【人教九上数学学霸提升作业】24.1.3 弧、弦、圆心角(附答案)
文档属性
| 名称 | 【人教九上数学学霸提升作业】24.1.3 弧、弦、圆心角(附答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 21:50:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.1.3 弧、弦、圆心角
命题点 1 弧、弦、圆心角之间的关系
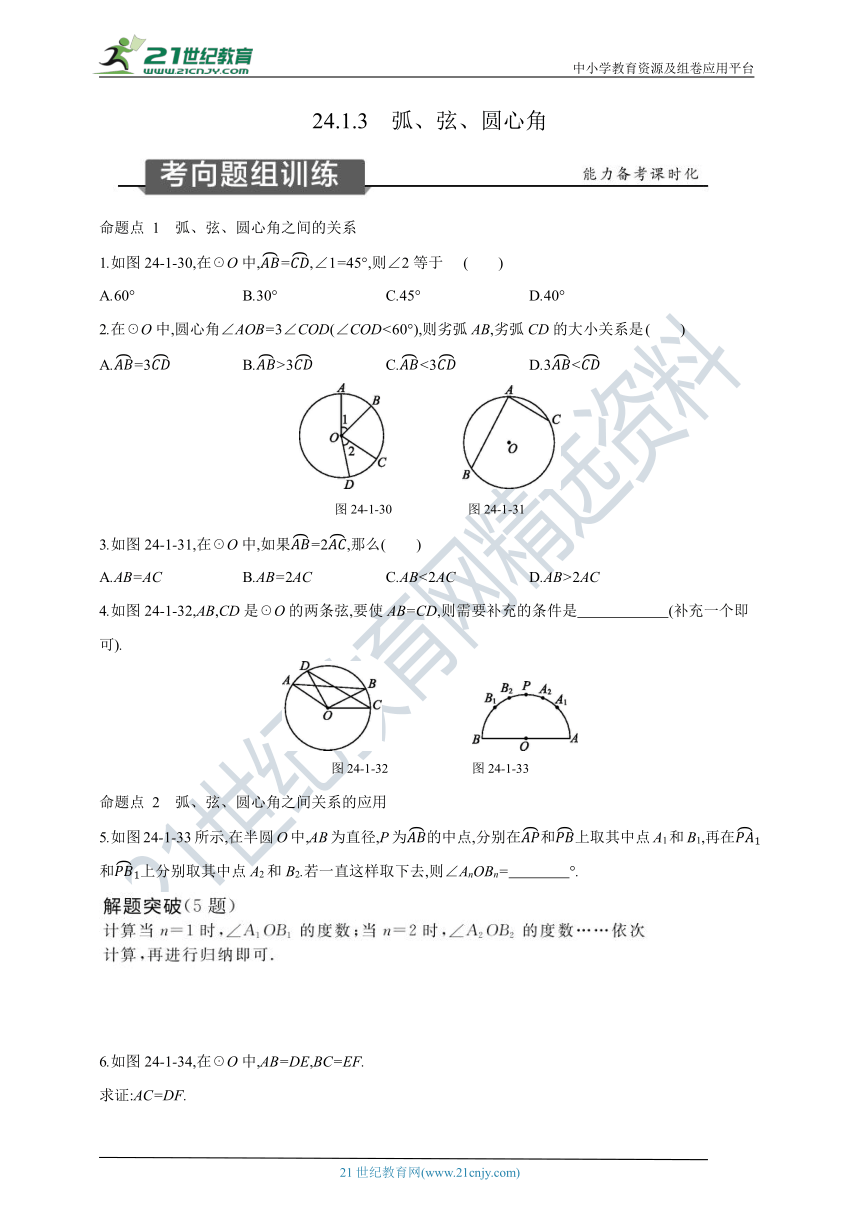
1.如图24-1-30,在☉O中,=,∠1=45°,则∠2等于 ( )
A.60° B.30° C.45° D.40°
2.在☉O中,圆心角∠AOB=3∠COD(∠COD<60°),则劣弧AB,劣弧CD的大小关系是 ( )
A.=3 B.>3 C.<3 D.3<
图24-1-30 图24-1-31
3.如图24-1-31,在☉O中,如果=2,那么( )
A.AB=AC B.AB=2AC C.AB<2AC D.AB>2AC
4.如图24-1-32,AB,CD是☉O的两条弦,要使AB=CD,则需要补充的条件是 (补充一个即可).
图24-1-32 图24-1-33
命题点 2 弧、弦、圆心角之间关系的应用
5.如图24-1-33所示,在半圆O中,AB为直径,P为的中点,分别在和上取其中点A1和B1,再在和上分别取其中点A2和B2.若一直这样取下去,则∠AnOBn= °.
6.如图24-1-34,在☉O中,AB=DE,BC=EF.
求证:AC=DF.
图24-1-34
7.如图24-1-35,在☉O中,M,N分别是半径OA,OB的中点,且CM⊥OA交☉O于点C,DN⊥OB交☉O于点D.求证:=.
图24-1-35
8.如图24-1-36,在☉O中,=2,AD⊥OC于点D.求证:AB=2AD.
图24-1-36
9.我们学习了“弧、弦、圆心角的关系”,事实上我们还可以得到“圆心角、弧、弦、弦心距之间的关系”.圆心角、弧、弦、弦心距之间的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们对应的其余各组量也相等.[弦心距是指从圆心到弦的距离(如图24-1-37①中的OC,OC'的长)]
请直接运用圆心角、弧、弦、弦心距之间的关系解决下列问题:
如图②,O是∠EPF的平分线上一点,以点O为圆心的圆与角的两边所在的直线分别交于点A,B和C,D.
(1)求证:AB=CD.
(2)若角的顶点P在圆上或圆内,(1)中的结论还成立吗 若不成立,请说明理由;若成立,请加以证明.
图24-1-37
10.只用圆规测量∠XOY的度数,方法是:以顶点O为圆心任意画一个圆,与角的两边分别交于点A,B(如图24-1-38),在这个圆上顺次截取=====…,这样绕着圆一周一周地截下去,直到绕第n周时,终于使第m(m>n)次截得的弧的末端恰好与点A重合,那么∠XOY的度数等于 .
图24-1-38
11.如图24-1-39,已知AB为☉O的直径,C为半圆上的动点(不与点A,B重合),过点C作弦CD⊥AB,∠OCD的平分线交☉O于点P,则点P的位置有何规律 请证明你的结论.
图24-1-39
典题讲评与答案详析
1.C
2.A [解析] 把∠AOB三等分,得到的每一份角所对的弧都等于,因此有=3.
3.C [解析] 取的中点D,则==,所以AD=BD=AC,而AD+BD>AB,所以2AC>AB.
4.=(答案不唯一)
5. [解析] 当n=1时,∠A1OB1=90°;当n=2时,∠A2OB2==45°……
所以∠AnOBn=°.
6.证明:∵AB=DE,BC=EF,
∴=,=,
∴+=+,
∴=,∴AC=DF.
7.证明:如图,连接OC,OD,
则OC=OD.
∵M,N分别是半径OA,OB的中点,
∴OM=OA,ON=OB.
又∵OA=OB,∴OM=ON.
∵CM⊥OA,DN⊥OB,
∴∠OMC=∠OND=90°.
在Rt△OMC和Rt△OND中,
∴Rt△OMC≌Rt△OND(HL),
∴∠MOC=∠NOD,∴=.
8.证明:如图,延长AD交☉O于点E.
∵OC⊥AD,
∴=2,AE=2AD.
∵=2,∴=,
∴AB=AE,∴AB=2AD.
9.解:(1)证明:如图①,过点O作OM⊥AB于点M,ON⊥CD于点N.
又∵PO平分∠EPF,∴OM=ON,
∴AB=CD.
(2)(1)中的结论还成立.
证明:当点P在☉O上时,如图②,同(1)知OM=ON,∴AB=CD;
当点P在☉O内时,如图③,同(1)知OM=ON,
∴AB=CD.
10.° [解析] 设∠XOY的度数为x,则mx=n×360°,所以x=°.
11.解:P为半圆的中点.
证明:如图,连接OP.
∵∠OCD的平分线交☉O于点P,
∴∠PCD=∠PCO.
∵OC=OP,∴∠PCO=∠OPC,
∴∠PCD=∠OPC,∴OP∥CD.
∵CD⊥AB,∴OP⊥AB,
∴=,即P为半圆的中点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.1.3 弧、弦、圆心角
命题点 1 弧、弦、圆心角之间的关系
1.如图24-1-30,在☉O中,=,∠1=45°,则∠2等于 ( )
A.60° B.30° C.45° D.40°
2.在☉O中,圆心角∠AOB=3∠COD(∠COD<60°),则劣弧AB,劣弧CD的大小关系是 ( )
A.=3 B.>3 C.<3 D.3<
图24-1-30 图24-1-31
3.如图24-1-31,在☉O中,如果=2,那么( )
A.AB=AC B.AB=2AC C.AB<2AC D.AB>2AC
4.如图24-1-32,AB,CD是☉O的两条弦,要使AB=CD,则需要补充的条件是 (补充一个即可).
图24-1-32 图24-1-33
命题点 2 弧、弦、圆心角之间关系的应用
5.如图24-1-33所示,在半圆O中,AB为直径,P为的中点,分别在和上取其中点A1和B1,再在和上分别取其中点A2和B2.若一直这样取下去,则∠AnOBn= °.
6.如图24-1-34,在☉O中,AB=DE,BC=EF.
求证:AC=DF.
图24-1-34
7.如图24-1-35,在☉O中,M,N分别是半径OA,OB的中点,且CM⊥OA交☉O于点C,DN⊥OB交☉O于点D.求证:=.
图24-1-35
8.如图24-1-36,在☉O中,=2,AD⊥OC于点D.求证:AB=2AD.
图24-1-36
9.我们学习了“弧、弦、圆心角的关系”,事实上我们还可以得到“圆心角、弧、弦、弦心距之间的关系”.圆心角、弧、弦、弦心距之间的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们对应的其余各组量也相等.[弦心距是指从圆心到弦的距离(如图24-1-37①中的OC,OC'的长)]
请直接运用圆心角、弧、弦、弦心距之间的关系解决下列问题:
如图②,O是∠EPF的平分线上一点,以点O为圆心的圆与角的两边所在的直线分别交于点A,B和C,D.
(1)求证:AB=CD.
(2)若角的顶点P在圆上或圆内,(1)中的结论还成立吗 若不成立,请说明理由;若成立,请加以证明.
图24-1-37
10.只用圆规测量∠XOY的度数,方法是:以顶点O为圆心任意画一个圆,与角的两边分别交于点A,B(如图24-1-38),在这个圆上顺次截取=====…,这样绕着圆一周一周地截下去,直到绕第n周时,终于使第m(m>n)次截得的弧的末端恰好与点A重合,那么∠XOY的度数等于 .
图24-1-38
11.如图24-1-39,已知AB为☉O的直径,C为半圆上的动点(不与点A,B重合),过点C作弦CD⊥AB,∠OCD的平分线交☉O于点P,则点P的位置有何规律 请证明你的结论.
图24-1-39
典题讲评与答案详析
1.C
2.A [解析] 把∠AOB三等分,得到的每一份角所对的弧都等于,因此有=3.
3.C [解析] 取的中点D,则==,所以AD=BD=AC,而AD+BD>AB,所以2AC>AB.
4.=(答案不唯一)
5. [解析] 当n=1时,∠A1OB1=90°;当n=2时,∠A2OB2==45°……
所以∠AnOBn=°.
6.证明:∵AB=DE,BC=EF,
∴=,=,
∴+=+,
∴=,∴AC=DF.
7.证明:如图,连接OC,OD,
则OC=OD.
∵M,N分别是半径OA,OB的中点,
∴OM=OA,ON=OB.
又∵OA=OB,∴OM=ON.
∵CM⊥OA,DN⊥OB,
∴∠OMC=∠OND=90°.
在Rt△OMC和Rt△OND中,
∴Rt△OMC≌Rt△OND(HL),
∴∠MOC=∠NOD,∴=.
8.证明:如图,延长AD交☉O于点E.
∵OC⊥AD,
∴=2,AE=2AD.
∵=2,∴=,
∴AB=AE,∴AB=2AD.
9.解:(1)证明:如图①,过点O作OM⊥AB于点M,ON⊥CD于点N.
又∵PO平分∠EPF,∴OM=ON,
∴AB=CD.
(2)(1)中的结论还成立.
证明:当点P在☉O上时,如图②,同(1)知OM=ON,∴AB=CD;
当点P在☉O内时,如图③,同(1)知OM=ON,
∴AB=CD.
10.° [解析] 设∠XOY的度数为x,则mx=n×360°,所以x=°.
11.解:P为半圆的中点.
证明:如图,连接OP.
∵∠OCD的平分线交☉O于点P,
∴∠PCD=∠PCO.
∵OC=OP,∴∠PCO=∠OPC,
∴∠PCD=∠OPC,∴OP∥CD.
∵CD⊥AB,∴OP⊥AB,
∴=,即P为半圆的中点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
