【人教九上数学学霸听课笔记】24.2.1 点和圆的位置关系 课件(共34张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】24.2.1 点和圆的位置关系 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 21:33:06 | ||
图片预览










文档简介
(共34张PPT)
24.2 点和圆、直线和圆的位置关系
第二十四章
圆
24.2.1 点和圆的位置关系
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
1.设⊙O的半径为r,点P到圆心的距离OP=d,则有:
点P在圆外 d________r;
点P在圆上 d________r;
点P在圆内 d________r.
>
=
<
2.________________上的三个点确定一个圆
3.经过三角形的三个______可以作一个圆,这个圆叫做三角
形的外接圆.外接圆的圆心是三角形三条边的____________
的交点,叫做这个三角形的外心.
4.假设命题的________不成立,由此经过推理得出矛盾,由矛
盾断定所作________不正确,从而得到________成立,这种
方法叫做反证法.
不在同一条直线
顶点
垂直平分线
结论
假设
原命题
目标一 理解点和圆的位置关系
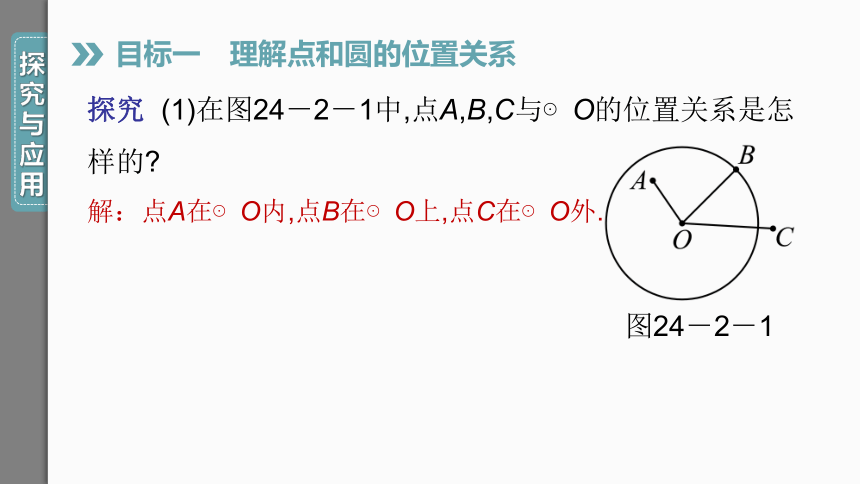
探究 (1)在图24-2-1中,点A,B,C与⊙O的位置关系是怎样的
解:点A在⊙O内,点B在⊙O上,点C在⊙O外.
图24-2-1
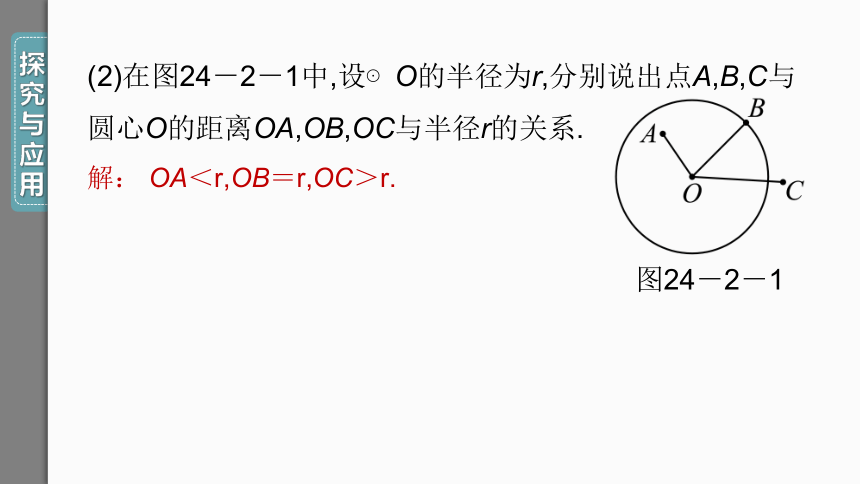
(2)在图24-2-1中,设⊙O的半径为r,分别说出点A,B,C与圆心O的距离OA,OB,OC与半径r的关系.
解: OA<r,OB=r,OC>r.
图24-2-1
(3)已知点P到圆心O的距离d和⊙O的半径r,能否判断点P和⊙O的位置关系
解:能.d>r 点P在⊙O外;d=r 点P在⊙O上;d例1 如图24-2-2,在Rt△ABC中,∠ACB=90°,BC=3 cm,AC=4 cm,以点B为圆心,BC长为半径作⊙B,则点A,C及AB,AC的中点D,E与⊙B有怎样的位置关系
[解析] 先求出点A,C,D,E与圆心B的距离,
再与半径3 cm进行比较.
图24-2-2
∵⊙B的半径为3 cm,AB=5 cm>3 cm,
∴点A在⊙B外;
∵BC=3 cm,∴点C在⊙B上;
∴点D在⊙B内;
∴点E在⊙B外.
判断点和圆的位置关系的方法
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
d>r 点P在________;
d=r 点P在________;
d归纳总结
圆外
圆上
圆内
目标二 会过不在同一条直线上的三个点作圆
探究 (1)作一个圆需要确定哪几个关键要素
解:作一个圆需要确定圆心的位置和半径的大小两个关键要素.
(2)经过一个已知点A作圆,你能作出多少个
解:可以作出无数个.
(3)如图24-2-3,经过两个已知点A,B作圆,你能作出多少个 圆心分布有什么特点
解:经过两个已知点A,B能作出无数个圆,
圆心都在线段AB的垂直平分线上,如图所示.
图24-2-3
(4)如图24-2-4,经过不在同一条直线上的三个点A,B,C能不能作圆 如果能,如何确定所作圆的圆心
图24-2-4
解:能.因为所求作的圆要经过A,B,C三点,所以圆心到这三点的距离相等,因此圆心既要在线段AB的垂直平分线上,又要在线段BC的垂直平分线上.作法如下:
①连接AB,BC;
②分别作出线段AB,BC的垂直平分线l1和l2,交于点O;
③以点O为圆心,OA为半径作圆,便可以作出经过点
A,B,C的圆(如图).
归纳
确定圆的条件与三角形的外心
不在________直线上的三个点确定________个圆.经过三角
形的三个顶点可以作________个圆,这个圆叫做三角形的外
接圆,外接圆的圆心叫做这个三角形的外心,则三角形的外
心是_________________________的交点.
同一条
一
一
三角形三条边的垂直平分线
例2 [教材练习第3题针对训练]图24-2-5是一块残破的轮片,试作出它所在圆的圆心和半径.
[解析] 若找出圆弧所在圆的圆心和半径,问题
也就得到解决了.又知道不在同一条直线上的
三点确定一个圆,故在圆弧上找三个点,即可通
过作弦的垂直平分线的方法确定圆心.
图24-2-5
解:(1)如图,在圆弧上依次取三点A,B,C;
(2)连接AB,BC;
(3)分别作AB,BC的垂直平分线a,b,两直线相交于点O,点O就是所求作的圆心;
(4)连接OB,OB就是这个圆的半径.
确定圆心的“三种方法”
(1)利用圆的轴对称性:将圆对折两次,确定圆的两条直径,
两直径的交点即为圆心,或根据垂径定理作两条不平行的弦
的垂直平分线,它们的交点即为圆心;
(2)利用圆周角定理的推论;
(3)根据不在同一条直线上的三个点确定一个圆的方法确定
圆心.
归纳总结
目标三 了解反证法的证明思想
思考 经过同一条直线上的三个点能作出一个圆吗 为什么
解:不能.理由:如图,假设经过同一条直线l上的A,B,C三点可以作一个圆.设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l,这与我们以前学过的“过一点有且
只有一条直线与已知直线垂直”矛盾.所以,经
过同一条直线上的三个点不能作出一个圆.
归纳
正难则反的解题思想方法——反证法
假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断
定所作假设不正确,从而得到原命题成立,这种方法叫做反
证法.
例3 [教材P94内容]用反证法证明“两直线平行,同位角相等”.
已知:如图24-2-6,AB∥CD,直线EF交AB于点O.
求证:∠1=∠2.(用反证法)
图24-2-6
证明:假设∠1≠∠2,过点O作直线A′B′,使∠EOB′=∠2.根据“同位角相等,两直线平行”,可得A′B′∥CD.这样,过点O就有两条直线AB,A′B′都平行于CD,这与平行公理“过直线外一点有且仅有一条直线与已知直线平行”矛盾.这说明∠1≠∠2不正确,从而∠1=∠2.
归纳
利用反证法证明的一般步骤
1.假设命题的结论不成立;
2.推理得出矛盾;
3.假设不成立,断定原命题的结论成立.
变式 求证:在一个三角形中,至少有一个内角小于或等于60°.
解:已知:△ABC.
求证:△ABC中至少有一个内角小于或等于60°.
证明:假设△ABC中没有一个内角小于或等于60°,即∠A>60°,∠B>60°,∠C>60°,于是∠A+∠B+∠C>60°+60°+60°=180°,这与“三角形的内角和等于180°”相矛盾,所以假设不成立,所以△ABC中至少有一个内角小于或等于60°.
1.⊙O的半径为6 cm,点A到圆心O的距离OA=4 cm,则点A与⊙O的位置关系为( )
A.点A在⊙O上 B.点A在⊙O内
C.点A在⊙O外 D.无法确定
B
2.下列说法正确的是( )
A.过一点A的圆的圆心可以是平面上任意点
B.过两点A,B的圆的圆心在一条直线上
C.过三点A,B,C的圆的圆心有且只有一点
D.过四点A,B,C,D的圆不存在
B
3.一个三角形的外心在其内部,则这个三角形是( )
A.任意三角形 B.直角三角形
C.锐角三角形 D.钝角三角形
C
4.在Rt△ABC中,∠C=90°,AC=6 cm,BC=8 cm,则它的外心与顶点C的距离为( )
A.5 cm B.6 cm
C.7 cm D.8 cm
A
5.已知:a∥b,a∥c,用反证法证明:b∥C.
证明:如图24-2-7,假设b与c不平行,则b与c________.
而a∥b,a∥c,
这与以前学过的“___________________________________”矛盾,
所以________.
图24-2-7
相交
过一点有且只有一条直线与已知直线平行
b∥c
https://www.21cnjy.com/help/help_extract.php
24.2 点和圆、直线和圆的位置关系
第二十四章
圆
24.2.1 点和圆的位置关系
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
1.设⊙O的半径为r,点P到圆心的距离OP=d,则有:
点P在圆外 d________r;
点P在圆上 d________r;
点P在圆内 d________r.
>
=
<
2.________________上的三个点确定一个圆
3.经过三角形的三个______可以作一个圆,这个圆叫做三角
形的外接圆.外接圆的圆心是三角形三条边的____________
的交点,叫做这个三角形的外心.
4.假设命题的________不成立,由此经过推理得出矛盾,由矛
盾断定所作________不正确,从而得到________成立,这种
方法叫做反证法.
不在同一条直线
顶点
垂直平分线
结论
假设
原命题
目标一 理解点和圆的位置关系
探究 (1)在图24-2-1中,点A,B,C与⊙O的位置关系是怎样的
解:点A在⊙O内,点B在⊙O上,点C在⊙O外.
图24-2-1
(2)在图24-2-1中,设⊙O的半径为r,分别说出点A,B,C与圆心O的距离OA,OB,OC与半径r的关系.
解: OA<r,OB=r,OC>r.
图24-2-1
(3)已知点P到圆心O的距离d和⊙O的半径r,能否判断点P和⊙O的位置关系
解:能.d>r 点P在⊙O外;d=r 点P在⊙O上;d
[解析] 先求出点A,C,D,E与圆心B的距离,
再与半径3 cm进行比较.
图24-2-2
∵⊙B的半径为3 cm,AB=5 cm>3 cm,
∴点A在⊙B外;
∵BC=3 cm,∴点C在⊙B上;
∴点D在⊙B内;
∴点E在⊙B外.
判断点和圆的位置关系的方法
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
d>r 点P在________;
d=r 点P在________;
d
圆外
圆上
圆内
目标二 会过不在同一条直线上的三个点作圆
探究 (1)作一个圆需要确定哪几个关键要素
解:作一个圆需要确定圆心的位置和半径的大小两个关键要素.
(2)经过一个已知点A作圆,你能作出多少个
解:可以作出无数个.
(3)如图24-2-3,经过两个已知点A,B作圆,你能作出多少个 圆心分布有什么特点
解:经过两个已知点A,B能作出无数个圆,
圆心都在线段AB的垂直平分线上,如图所示.
图24-2-3
(4)如图24-2-4,经过不在同一条直线上的三个点A,B,C能不能作圆 如果能,如何确定所作圆的圆心
图24-2-4
解:能.因为所求作的圆要经过A,B,C三点,所以圆心到这三点的距离相等,因此圆心既要在线段AB的垂直平分线上,又要在线段BC的垂直平分线上.作法如下:
①连接AB,BC;
②分别作出线段AB,BC的垂直平分线l1和l2,交于点O;
③以点O为圆心,OA为半径作圆,便可以作出经过点
A,B,C的圆(如图).
归纳
确定圆的条件与三角形的外心
不在________直线上的三个点确定________个圆.经过三角
形的三个顶点可以作________个圆,这个圆叫做三角形的外
接圆,外接圆的圆心叫做这个三角形的外心,则三角形的外
心是_________________________的交点.
同一条
一
一
三角形三条边的垂直平分线
例2 [教材练习第3题针对训练]图24-2-5是一块残破的轮片,试作出它所在圆的圆心和半径.
[解析] 若找出圆弧所在圆的圆心和半径,问题
也就得到解决了.又知道不在同一条直线上的
三点确定一个圆,故在圆弧上找三个点,即可通
过作弦的垂直平分线的方法确定圆心.
图24-2-5
解:(1)如图,在圆弧上依次取三点A,B,C;
(2)连接AB,BC;
(3)分别作AB,BC的垂直平分线a,b,两直线相交于点O,点O就是所求作的圆心;
(4)连接OB,OB就是这个圆的半径.
确定圆心的“三种方法”
(1)利用圆的轴对称性:将圆对折两次,确定圆的两条直径,
两直径的交点即为圆心,或根据垂径定理作两条不平行的弦
的垂直平分线,它们的交点即为圆心;
(2)利用圆周角定理的推论;
(3)根据不在同一条直线上的三个点确定一个圆的方法确定
圆心.
归纳总结
目标三 了解反证法的证明思想
思考 经过同一条直线上的三个点能作出一个圆吗 为什么
解:不能.理由:如图,假设经过同一条直线l上的A,B,C三点可以作一个圆.设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l,这与我们以前学过的“过一点有且
只有一条直线与已知直线垂直”矛盾.所以,经
过同一条直线上的三个点不能作出一个圆.
归纳
正难则反的解题思想方法——反证法
假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断
定所作假设不正确,从而得到原命题成立,这种方法叫做反
证法.
例3 [教材P94内容]用反证法证明“两直线平行,同位角相等”.
已知:如图24-2-6,AB∥CD,直线EF交AB于点O.
求证:∠1=∠2.(用反证法)
图24-2-6
证明:假设∠1≠∠2,过点O作直线A′B′,使∠EOB′=∠2.根据“同位角相等,两直线平行”,可得A′B′∥CD.这样,过点O就有两条直线AB,A′B′都平行于CD,这与平行公理“过直线外一点有且仅有一条直线与已知直线平行”矛盾.这说明∠1≠∠2不正确,从而∠1=∠2.
归纳
利用反证法证明的一般步骤
1.假设命题的结论不成立;
2.推理得出矛盾;
3.假设不成立,断定原命题的结论成立.
变式 求证:在一个三角形中,至少有一个内角小于或等于60°.
解:已知:△ABC.
求证:△ABC中至少有一个内角小于或等于60°.
证明:假设△ABC中没有一个内角小于或等于60°,即∠A>60°,∠B>60°,∠C>60°,于是∠A+∠B+∠C>60°+60°+60°=180°,这与“三角形的内角和等于180°”相矛盾,所以假设不成立,所以△ABC中至少有一个内角小于或等于60°.
1.⊙O的半径为6 cm,点A到圆心O的距离OA=4 cm,则点A与⊙O的位置关系为( )
A.点A在⊙O上 B.点A在⊙O内
C.点A在⊙O外 D.无法确定
B
2.下列说法正确的是( )
A.过一点A的圆的圆心可以是平面上任意点
B.过两点A,B的圆的圆心在一条直线上
C.过三点A,B,C的圆的圆心有且只有一点
D.过四点A,B,C,D的圆不存在
B
3.一个三角形的外心在其内部,则这个三角形是( )
A.任意三角形 B.直角三角形
C.锐角三角形 D.钝角三角形
C
4.在Rt△ABC中,∠C=90°,AC=6 cm,BC=8 cm,则它的外心与顶点C的距离为( )
A.5 cm B.6 cm
C.7 cm D.8 cm
A
5.已知:a∥b,a∥c,用反证法证明:b∥C.
证明:如图24-2-7,假设b与c不平行,则b与c________.
而a∥b,a∥c,
这与以前学过的“___________________________________”矛盾,
所以________.
图24-2-7
相交
过一点有且只有一条直线与已知直线平行
b∥c
https://www.21cnjy.com/help/help_extract.php
同课章节目录
