【人教九上数学学霸听课笔记】24.2.2 第1课时 直线和圆的位置关系 课件(共27张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】24.2.2 第1课时 直线和圆的位置关系 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 21:32:18 | ||
图片预览




文档简介
(共27张PPT)
24.2.2 直线和圆的位置关系
第二十四章
圆
第1课时 直线和圆的位置关系
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
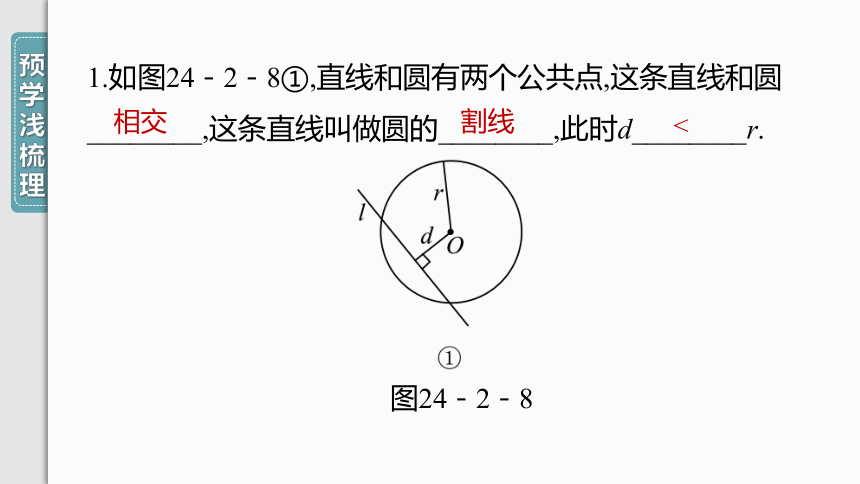
1.如图24-2-8①,直线和圆有两个公共点,这条直线和圆________,这条直线叫做圆的________,此时d________r.
图24-2-8
相交
割线
<
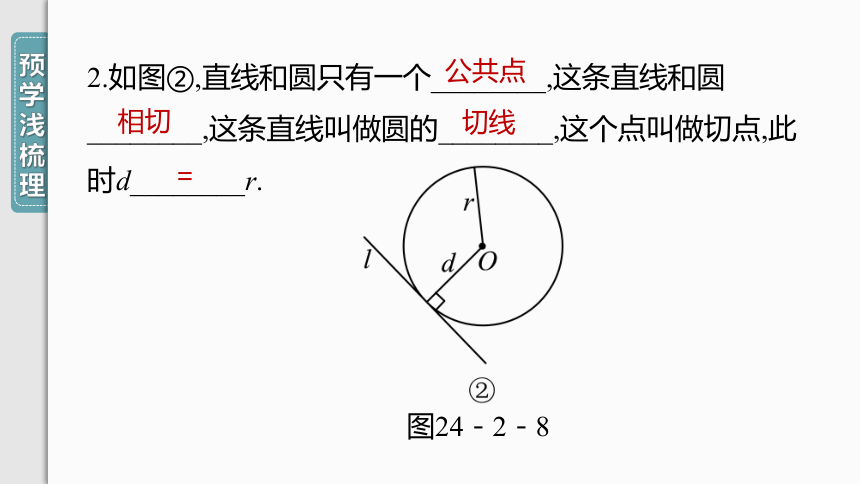
2.如图②,直线和圆只有一个________,这条直线和圆________,这条直线叫做圆的________,这个点叫做切点,此时d________r.
图24-2-8
公共点
相切
切线
=
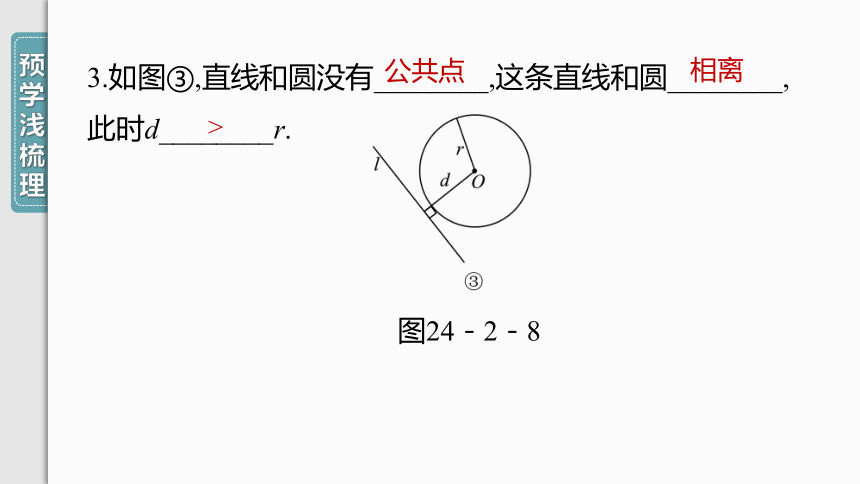
3.如图③,直线和圆没有________,这条直线和圆________,此时d________r.
图24-2-8
公共点
相离
>
目标一 理解直线和圆的三种位置关系的定义
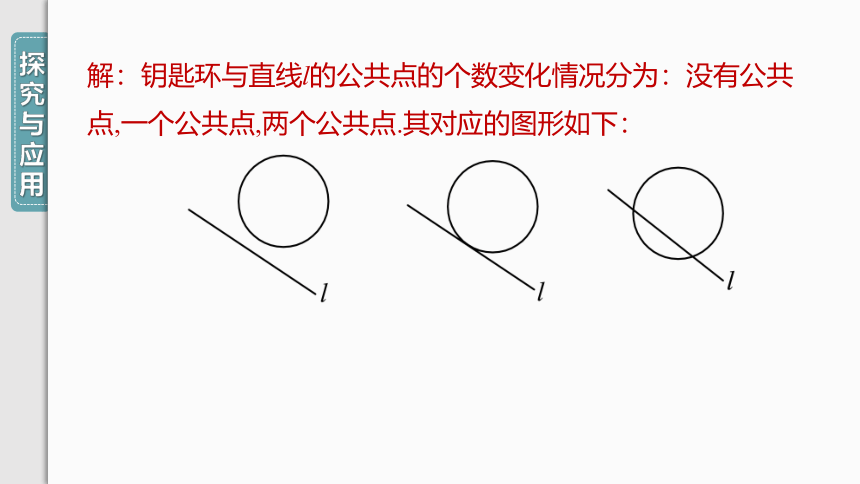
问题 如图24-2-9,在纸上画一条直线l,把钥匙环看作一个圆,在纸上移动钥匙环,请你说出在移动钥匙环的过程中,它与直线l的公共点的个数的变化情况,并画出不同情况下,圆环与直线呈现的位置关系图形.
图24-2-9
解:钥匙环与直线l的公共点的个数变化情况分为:没有公共点,一个公共点,两个公共点.其对应的图形如下:
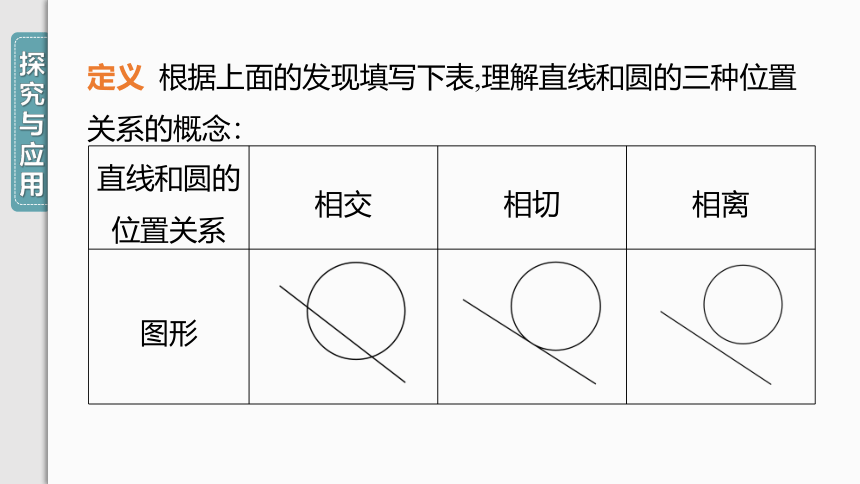
定义 根据上面的发现填写下表,理解直线和圆的三种位置关系的概念:
直线和圆的位置关系 相交 相切 相离
图形
直线和圆的位置关系 相交 相切 相离
概念 直线和圆有______个公共点,这时我们说这条直线和圆相交 直线和圆只有______个公共点,这时我们说这条直线和圆相切 直线和圆______公共点,这时我们说这条直线和圆相离
两
一
没有
直线和圆的位置关系 相交 相切 相离
公共点 的名称 交点 切点
直线的名称 割线 切线
目标二 理解直线和圆相交、相切、相离的判定方法和
性质
思考 设⊙O的半径为r,圆心O到直线l的距离为d,画出直线l和⊙O的不同位置关系的图形,并画出表示距离d与半径r的线段,判断d与r的大小关系.反过来,你能根据d与r的大小关系确定直线和圆的位置关系吗
解:图形如下:
直线和圆相交、相切、相离时,d和r对应的关系如下:
直线l和⊙O相交 d直线l和⊙O相切 d=r;
直线l和⊙O相离 d>r.
例1 在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,以点C为圆心,r为半径的圆与直线AB有怎样的位置关系 为什么
(1)r=2 cm;(2)r=2.4 cm;(3)r=3 cm.
[解析] 欲判断⊙C与直线AB的位置关系,需先求出圆心C到直线AB的距离,然后与r比较大小即可.
解:如图所示,过点C作CD⊥AB于点D.
∵∠ACB=90°,
∴CD=2.4 cm=d.
(1)∵d=2.4 cm>r=2 cm,
∴⊙C与直线AB相离.
(2)∵d=2.4 cm=r=2.4 cm,
∴⊙C与直线AB相切.
(3)∵d=2.4 cm<r=3 cm,
∴⊙C与直线AB相交.
判断直线和圆的位置关系的“三步法”
方法总结
求值
根据题意求出圆心到直线的距离d和圆的半径r
比较
比较d与r的大小
结论
根据d与r的大小关系判断直线和圆的位置关系
例2 如图24-2-10,在Rt△ABC中,∠C=90°,AC=6,AB=10,若以点C为圆心,r为半径作圆,则:
(1)当直线AB与⊙C相切时,求r的值;
(2)当直线AB与⊙C相离时,求r的取值范围.
图24-2-10
解:(1)过点C作CD⊥AB于点D.
∵在Rt△ABC中,AC=6,AB=10,
∴CD=4.8,即d=4.8.
∵当直线AB与⊙C相切时,d=r,∴r=4.8.
(2)由(1)知,圆心C到直线AB的距离d=4.8.
∵当直线AB与⊙C相离时,d>r,∴0D
变式 在△ABC中,∠C=90°,AC=3,BC=4,如图J24-2-1.以点C为圆心,R为半径画圆,若⊙C与AB边只有一个公共点,求R的取值范围.
图J24-2-1
解:①如图,当⊙C与AB边相切时,⊙C与AB边只有一个公共点,此时R等于点C到AB的距离.过点C作CD⊥AB于点D.
②当31.已知⊙O的半径为4,圆心O到直线l的距离为d,若d=2,则⊙O与直线l________;若d=4,则⊙O与直线l________;若d=6,则⊙O与直线l________.
相交
相切
相离
2.在平面直角坐标系中,以点(3,-2)为圆心,2为半径的圆与y轴________,与x轴________.
相离
相切
3.如图24-2-11,在Rt△ABC中,∠C=90°,∠B=30°,BC=4 cm,以点C为圆心,r cm为半径作圆,若________,则⊙C与直线AB相离;若________,则⊙C与直线AB相切;若________,则⊙C与直线AB相交.
图24-2-11
0r=2
r>2
4.已知⊙O的半径为2 cm,直线l上有一点P,OP=2 cm,则直线l与⊙O的位置关系是______________.
相交或相切
https://www.21cnjy.com/help/help_extract.php
24.2.2 直线和圆的位置关系
第二十四章
圆
第1课时 直线和圆的位置关系
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
1.如图24-2-8①,直线和圆有两个公共点,这条直线和圆________,这条直线叫做圆的________,此时d________r.
图24-2-8
相交
割线
<
2.如图②,直线和圆只有一个________,这条直线和圆________,这条直线叫做圆的________,这个点叫做切点,此时d________r.
图24-2-8
公共点
相切
切线
=
3.如图③,直线和圆没有________,这条直线和圆________,此时d________r.
图24-2-8
公共点
相离
>
目标一 理解直线和圆的三种位置关系的定义
问题 如图24-2-9,在纸上画一条直线l,把钥匙环看作一个圆,在纸上移动钥匙环,请你说出在移动钥匙环的过程中,它与直线l的公共点的个数的变化情况,并画出不同情况下,圆环与直线呈现的位置关系图形.
图24-2-9
解:钥匙环与直线l的公共点的个数变化情况分为:没有公共点,一个公共点,两个公共点.其对应的图形如下:
定义 根据上面的发现填写下表,理解直线和圆的三种位置关系的概念:
直线和圆的位置关系 相交 相切 相离
图形
直线和圆的位置关系 相交 相切 相离
概念 直线和圆有______个公共点,这时我们说这条直线和圆相交 直线和圆只有______个公共点,这时我们说这条直线和圆相切 直线和圆______公共点,这时我们说这条直线和圆相离
两
一
没有
直线和圆的位置关系 相交 相切 相离
公共点 的名称 交点 切点
直线的名称 割线 切线
目标二 理解直线和圆相交、相切、相离的判定方法和
性质
思考 设⊙O的半径为r,圆心O到直线l的距离为d,画出直线l和⊙O的不同位置关系的图形,并画出表示距离d与半径r的线段,判断d与r的大小关系.反过来,你能根据d与r的大小关系确定直线和圆的位置关系吗
解:图形如下:
直线和圆相交、相切、相离时,d和r对应的关系如下:
直线l和⊙O相交 d
直线l和⊙O相离 d>r.
例1 在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,以点C为圆心,r为半径的圆与直线AB有怎样的位置关系 为什么
(1)r=2 cm;(2)r=2.4 cm;(3)r=3 cm.
[解析] 欲判断⊙C与直线AB的位置关系,需先求出圆心C到直线AB的距离,然后与r比较大小即可.
解:如图所示,过点C作CD⊥AB于点D.
∵∠ACB=90°,
∴CD=2.4 cm=d.
(1)∵d=2.4 cm>r=2 cm,
∴⊙C与直线AB相离.
(2)∵d=2.4 cm=r=2.4 cm,
∴⊙C与直线AB相切.
(3)∵d=2.4 cm<r=3 cm,
∴⊙C与直线AB相交.
判断直线和圆的位置关系的“三步法”
方法总结
求值
根据题意求出圆心到直线的距离d和圆的半径r
比较
比较d与r的大小
结论
根据d与r的大小关系判断直线和圆的位置关系
例2 如图24-2-10,在Rt△ABC中,∠C=90°,AC=6,AB=10,若以点C为圆心,r为半径作圆,则:
(1)当直线AB与⊙C相切时,求r的值;
(2)当直线AB与⊙C相离时,求r的取值范围.
图24-2-10
解:(1)过点C作CD⊥AB于点D.
∵在Rt△ABC中,AC=6,AB=10,
∴CD=4.8,即d=4.8.
∵当直线AB与⊙C相切时,d=r,∴r=4.8.
(2)由(1)知,圆心C到直线AB的距离d=4.8.
∵当直线AB与⊙C相离时,d>r,∴0
变式 在△ABC中,∠C=90°,AC=3,BC=4,如图J24-2-1.以点C为圆心,R为半径画圆,若⊙C与AB边只有一个公共点,求R的取值范围.
图J24-2-1
解:①如图,当⊙C与AB边相切时,⊙C与AB边只有一个公共点,此时R等于点C到AB的距离.过点C作CD⊥AB于点D.
②当3
相交
相切
相离
2.在平面直角坐标系中,以点(3,-2)为圆心,2为半径的圆与y轴________,与x轴________.
相离
相切
3.如图24-2-11,在Rt△ABC中,∠C=90°,∠B=30°,BC=4 cm,以点C为圆心,r cm为半径作圆,若________,则⊙C与直线AB相离;若________,则⊙C与直线AB相切;若________,则⊙C与直线AB相交.
图24-2-11
0
r>2
4.已知⊙O的半径为2 cm,直线l上有一点P,OP=2 cm,则直线l与⊙O的位置关系是______________.
相交或相切
https://www.21cnjy.com/help/help_extract.php
同课章节目录
