【人教九上数学学霸听课笔记】24.2.2 第2课时 切线的判定和性质 课件(共25张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】24.2.2 第2课时 切线的判定和性质 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 21:31:15 | ||
图片预览





文档简介
(共23张PPT)
第2课时 切线的判定和性质
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
24.2.2 直线和圆的位置关系
1.切线的判定定理:经过半径的________并且________这
条半径的直线是圆的切线.
2.切线的性质定理:圆的切线________过切点的半径.
外端
垂直于
垂直于
目标一 理解并掌握切线的判定定理
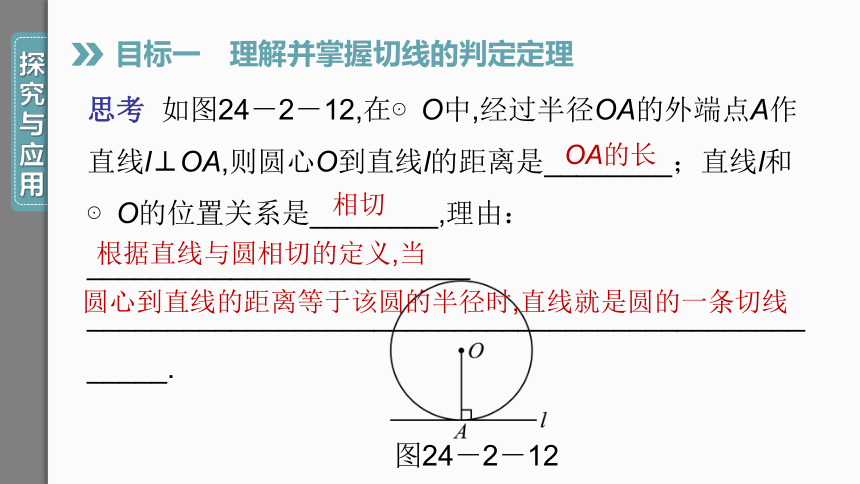
思考 如图24-2-12,在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离是________;直线l和⊙O的位置关系是________,理由:________________________
__________________________________________________.
图24-2-12
OA的长
相切
根据直线与圆相切的定义,当
圆心到直线的距离等于该圆的半径时,直线就是圆的一条切线
归纳
切线的判定定理
经过半径的________并且________这条半径的直线是圆的
切线.
外端
垂直于
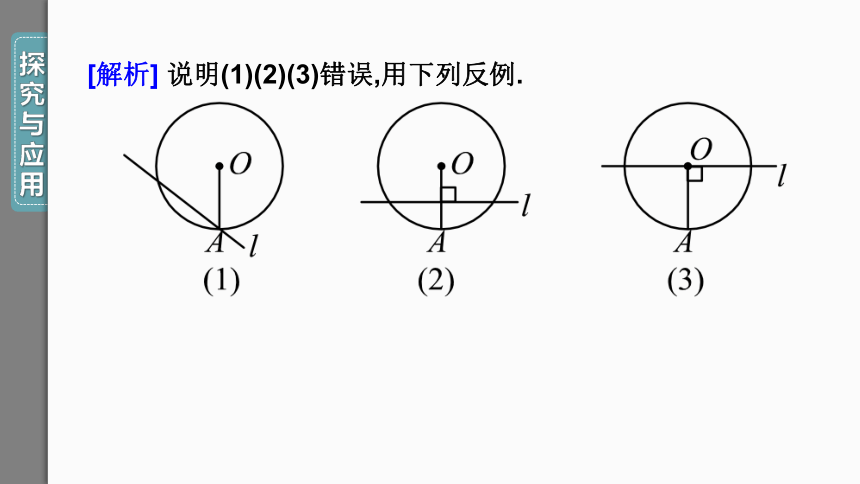
例1 判断下列说法是否正确:
(1)过半径外端的直线是圆的切线.( )
(2)与半径垂直的直线是圆的切线.( )
(3)过半径的端点且与半径垂直的直线是圆的切线.( )
(4)经过直径的端点且与该直径垂直的直线是圆的切线.
( )
×
×
×
√
[解析] 说明(1)(2)(3)错误,用下列反例.
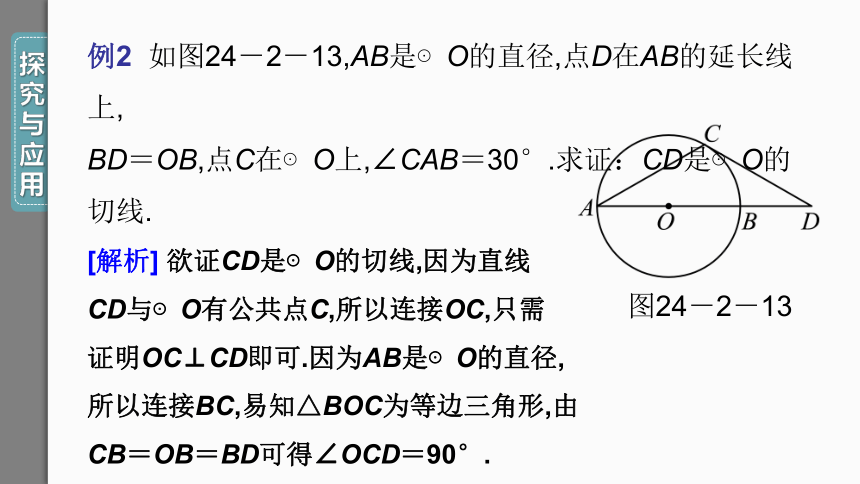
例2 如图24-2-13,AB是⊙O的直径,点D在AB的延长线上,
BD=OB,点C在⊙O上,∠CAB=30°.求证:CD是⊙O的切线.
[解析] 欲证CD是⊙O的切线,因为直线
CD与⊙O有公共点C,所以连接OC,只需
证明OC⊥CD即可.因为AB是⊙O的直径,
所以连接BC,易知△BOC为等边三角形,由
CB=OB=BD可得∠OCD=90°.
图24-2-13
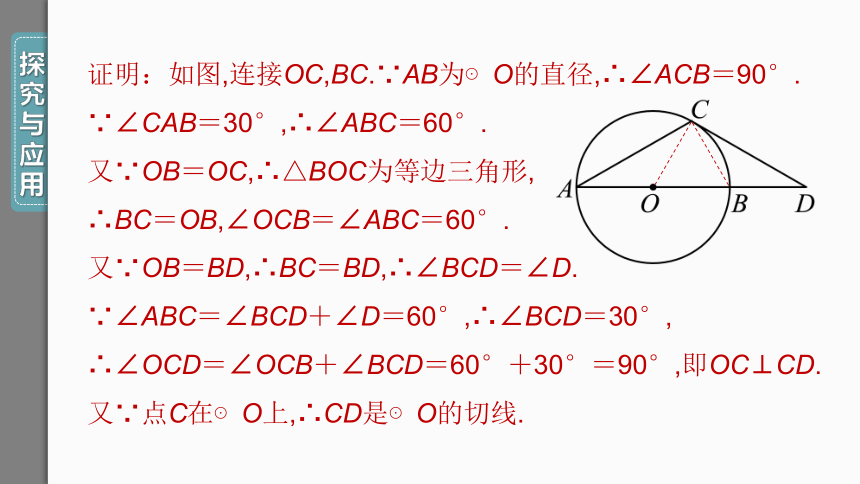
证明:如图,连接OC,BC.∵AB为⊙O的直径,∴∠ACB=90°.
∵∠CAB=30°,∴∠ABC=60°.
又∵OB=OC,∴△BOC为等边三角形,
∴BC=OB,∠OCB=∠ABC=60°.
又∵OB=BD,∴BC=BD,∴∠BCD=∠D.
∵∠ABC=∠BCD+∠D=60°,∴∠BCD=30°,
∴∠OCD=∠OCB+∠BCD=60°+30°=90°,即OC⊥CD.
又∵点C在⊙O上,∴CD是⊙O的切线.
判定圆的切线的“三种方法”
1.定义法:和圆有且只有一个公共点的直线是圆的切线;
2.求值法(d=r):与圆心的距离等于圆的半径的直线是圆的
切线;
3.判定定理:经过半径的外端并且垂直于这条半径的直线
是圆的切线.
方法总结
目标二 理解并掌握切线的性质定理
思考 将“目标一思考”中的问题反过来,如图24-2-14,如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢 证明你的结论.
图24-2-14
解:半径OA⊥l.
证明:假设直线l不垂直于半径OA,过点O作OA′⊥l,垂足为A′.
根据垂线段最短,可得OA′例3 如图24-2-15,AB为⊙O的直径,PQ切⊙O于点E,AC⊥
PQ于点C.求证:AE平分∠BAC.
证明:连接OE,如图.
∵OA=OE,∴∠OEA=∠OAE.
∵PQ切⊙O于点E,∴OE⊥PQ.
又∵AC⊥PQ,∴OE∥AC,
∴∠OEA=∠EAC,
∴∠OAE=∠EAC,∴AE平分∠BAC.
图24-2-15
目标三 能综合运用切线的判定定理和性质定理解决问题
例4 [教材P98例1]如图24-2-16,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.
图24-2-16
证明:如图,过点O作OE⊥AC,垂足为E,连接OD,OA.
∵⊙O与AB相切于点D,
∴OD⊥AB.
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO是∠BAC的平分线,
∴OE=OD,即OE是⊙O的半径.
这样,AC经过⊙O的半径OE的外端点E,并且垂直于半径OE,故AC与⊙O相切.
变式 如图J24-2-2,已知AB是⊙O的直径,直线BC与⊙O相切于点B,过点A作AD∥OC交⊙O于点D,连接CD.求证:CD是⊙O的切线.
证明:连接OD,如图所示.
∵OA=OD,∴∠ODA=∠OAD.
∵AD∥OC,
∴∠COD=∠ODA,∠COB=∠OAD,
∴∠COD=∠COB.
图J24-2-2
又∵OD=OB,OC=OC,
∴△ODC≌△OBC(SAS),
∴∠ODC=∠OBC.
∵BC与⊙O相切于点B,
∴∠OBC=90°,∴∠ODC=90°,
∴OD⊥CD.
又∵CD经过半径OD的外端点D,
∴CD是⊙O的切线.
判定圆的切线的常用辅助线的选择
1.如果已知直线过圆上一点,那么连接这点和圆心,得到半径,
证明这条半径垂直于已知直线即可,简记为:有交点,作半
径,证垂直.
2.如果已知直线与圆没有明确是否有公共点,那么过圆心作
已知直线的垂线段,证明垂线段等于半径即可,可简记为:
无交点,作垂线,证半径.
方法总结
1.如图24-2-17,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
A.70° B.35°
C.20° D.40°
图24-2-17
D
[解析] ∵AC是⊙O的切线,AB是⊙O的直径,∴AB⊥AC,即∠CAB=90°.
∵∠C=70°,∴∠CBA=20°,∴∠AOD=40°.
故选D.
2.如图24-2-18,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,以点O为圆心,OC为半径作半圆.求证:AB为⊙O的切线.
证明:如图,过点O作OH⊥AB于点H.
∵AO平分∠BAC,OC⊥AC,
OH⊥AB,∴OH=OC,
∴AB为⊙O的切线.
图24-2-18
3.如图24-2-19,在△ABC中,∠CAB=90°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.求证:直线ED与⊙O相切.
图24-2-19
证明:连接OE,OD.在△OAE与△ODE中,
∴△OAE≌△ODE(SSS),
∴∠ODE=∠CAB=90°,即 OD⊥DE.
又∵OD是⊙O的半径,
∴直线ED与⊙O相切.
第2课时 切线的判定和性质
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
24.2.2 直线和圆的位置关系
1.切线的判定定理:经过半径的________并且________这
条半径的直线是圆的切线.
2.切线的性质定理:圆的切线________过切点的半径.
外端
垂直于
垂直于
目标一 理解并掌握切线的判定定理
思考 如图24-2-12,在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离是________;直线l和⊙O的位置关系是________,理由:________________________
__________________________________________________.
图24-2-12
OA的长
相切
根据直线与圆相切的定义,当
圆心到直线的距离等于该圆的半径时,直线就是圆的一条切线
归纳
切线的判定定理
经过半径的________并且________这条半径的直线是圆的
切线.
外端
垂直于
例1 判断下列说法是否正确:
(1)过半径外端的直线是圆的切线.( )
(2)与半径垂直的直线是圆的切线.( )
(3)过半径的端点且与半径垂直的直线是圆的切线.( )
(4)经过直径的端点且与该直径垂直的直线是圆的切线.
( )
×
×
×
√
[解析] 说明(1)(2)(3)错误,用下列反例.
例2 如图24-2-13,AB是⊙O的直径,点D在AB的延长线上,
BD=OB,点C在⊙O上,∠CAB=30°.求证:CD是⊙O的切线.
[解析] 欲证CD是⊙O的切线,因为直线
CD与⊙O有公共点C,所以连接OC,只需
证明OC⊥CD即可.因为AB是⊙O的直径,
所以连接BC,易知△BOC为等边三角形,由
CB=OB=BD可得∠OCD=90°.
图24-2-13
证明:如图,连接OC,BC.∵AB为⊙O的直径,∴∠ACB=90°.
∵∠CAB=30°,∴∠ABC=60°.
又∵OB=OC,∴△BOC为等边三角形,
∴BC=OB,∠OCB=∠ABC=60°.
又∵OB=BD,∴BC=BD,∴∠BCD=∠D.
∵∠ABC=∠BCD+∠D=60°,∴∠BCD=30°,
∴∠OCD=∠OCB+∠BCD=60°+30°=90°,即OC⊥CD.
又∵点C在⊙O上,∴CD是⊙O的切线.
判定圆的切线的“三种方法”
1.定义法:和圆有且只有一个公共点的直线是圆的切线;
2.求值法(d=r):与圆心的距离等于圆的半径的直线是圆的
切线;
3.判定定理:经过半径的外端并且垂直于这条半径的直线
是圆的切线.
方法总结
目标二 理解并掌握切线的性质定理
思考 将“目标一思考”中的问题反过来,如图24-2-14,如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢 证明你的结论.
图24-2-14
解:半径OA⊥l.
证明:假设直线l不垂直于半径OA,过点O作OA′⊥l,垂足为A′.
根据垂线段最短,可得OA′
PQ于点C.求证:AE平分∠BAC.
证明:连接OE,如图.
∵OA=OE,∴∠OEA=∠OAE.
∵PQ切⊙O于点E,∴OE⊥PQ.
又∵AC⊥PQ,∴OE∥AC,
∴∠OEA=∠EAC,
∴∠OAE=∠EAC,∴AE平分∠BAC.
图24-2-15
目标三 能综合运用切线的判定定理和性质定理解决问题
例4 [教材P98例1]如图24-2-16,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.
图24-2-16
证明:如图,过点O作OE⊥AC,垂足为E,连接OD,OA.
∵⊙O与AB相切于点D,
∴OD⊥AB.
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO是∠BAC的平分线,
∴OE=OD,即OE是⊙O的半径.
这样,AC经过⊙O的半径OE的外端点E,并且垂直于半径OE,故AC与⊙O相切.
变式 如图J24-2-2,已知AB是⊙O的直径,直线BC与⊙O相切于点B,过点A作AD∥OC交⊙O于点D,连接CD.求证:CD是⊙O的切线.
证明:连接OD,如图所示.
∵OA=OD,∴∠ODA=∠OAD.
∵AD∥OC,
∴∠COD=∠ODA,∠COB=∠OAD,
∴∠COD=∠COB.
图J24-2-2
又∵OD=OB,OC=OC,
∴△ODC≌△OBC(SAS),
∴∠ODC=∠OBC.
∵BC与⊙O相切于点B,
∴∠OBC=90°,∴∠ODC=90°,
∴OD⊥CD.
又∵CD经过半径OD的外端点D,
∴CD是⊙O的切线.
判定圆的切线的常用辅助线的选择
1.如果已知直线过圆上一点,那么连接这点和圆心,得到半径,
证明这条半径垂直于已知直线即可,简记为:有交点,作半
径,证垂直.
2.如果已知直线与圆没有明确是否有公共点,那么过圆心作
已知直线的垂线段,证明垂线段等于半径即可,可简记为:
无交点,作垂线,证半径.
方法总结
1.如图24-2-17,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
A.70° B.35°
C.20° D.40°
图24-2-17
D
[解析] ∵AC是⊙O的切线,AB是⊙O的直径,∴AB⊥AC,即∠CAB=90°.
∵∠C=70°,∴∠CBA=20°,∴∠AOD=40°.
故选D.
2.如图24-2-18,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,以点O为圆心,OC为半径作半圆.求证:AB为⊙O的切线.
证明:如图,过点O作OH⊥AB于点H.
∵AO平分∠BAC,OC⊥AC,
OH⊥AB,∴OH=OC,
∴AB为⊙O的切线.
图24-2-18
3.如图24-2-19,在△ABC中,∠CAB=90°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.求证:直线ED与⊙O相切.
图24-2-19
证明:连接OE,OD.在△OAE与△ODE中,
∴△OAE≌△ODE(SSS),
∴∠ODE=∠CAB=90°,即 OD⊥DE.
又∵OD是⊙O的半径,
∴直线ED与⊙O相切.
同课章节目录
