【人教九上数学学霸听课笔记】24.2.2第3课时 切线长定理和三角形的内切圆 课件(共31张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】24.2.2第3课时 切线长定理和三角形的内切圆 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 21:30:30 | ||
图片预览








文档简介
(共31张PPT)
24.2.2 直线和圆的位置关系
第二十四章
圆
第3课时 切线长定理和三角形的内切圆
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
1.从圆外一点可以引圆的两条切线,它们的________相等,这
一点和圆心的连线平分________________.
2.与三角形各边都________的圆叫做三角形的内切圆;内
切圆的圆心是三角形______________的交点,叫做三角形的
内心.
切线长
两条切线的夹角
相切
三条角平分线
目标一 理解切线长的概念,掌握切线长定理
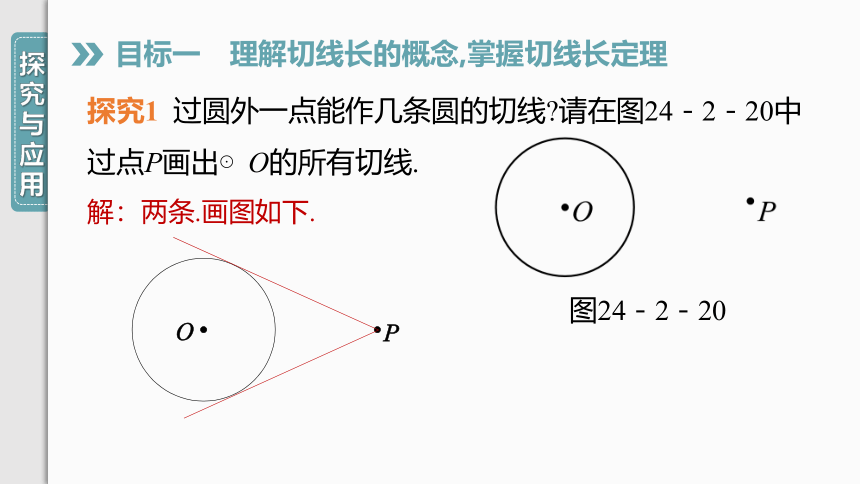
探究1 过圆外一点能作几条圆的切线 请在图24-2-20中过点P画出⊙O的所有切线.
解:两条.画图如下.
图24-2-20
定义 经过圆外一点的圆的切线上,这点和________之间线
段的长,叫做这点到圆的切线长.
切点
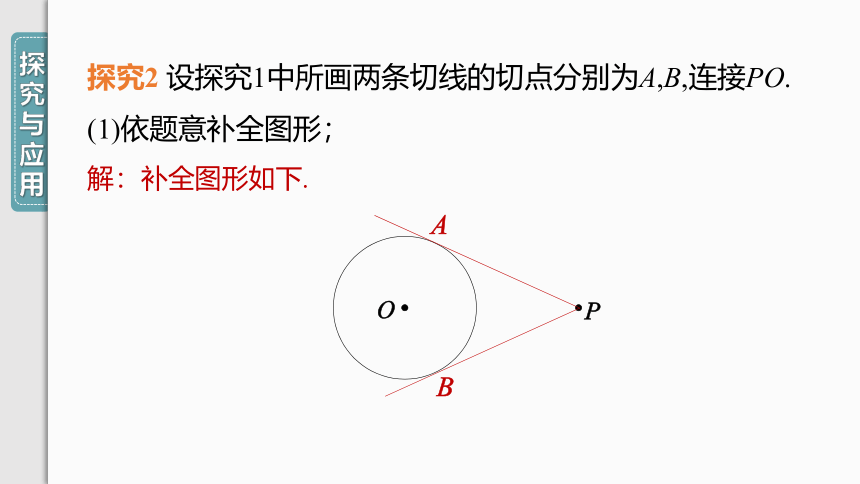
探究2 设探究1中所画两条切线的切点分别为A,B,连接PO.
(1)依题意补全图形;
解:补全图形如下.
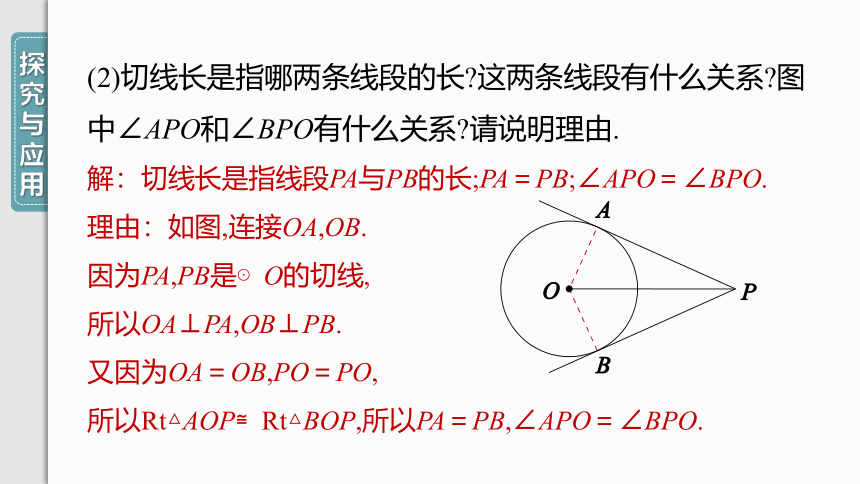
(2)切线长是指哪两条线段的长 这两条线段有什么关系 图中∠APO和∠BPO有什么关系 请说明理由.
解:切线长是指线段PA与PB的长;PA=PB;∠APO=∠BPO.
理由:如图,连接OA,OB.
因为PA,PB是⊙O的切线,
所以OA⊥PA,OB⊥PB.
又因为OA=OB,PO=PO,
所以Rt△AOP≌Rt△BOP,所以PA=PB,∠APO=∠BPO.
总结
切线长定理
从圆外一点可以引圆的两条切线,它们的________相等,这
一点和圆心的连线平分________________.
切线长
两条切线的夹角
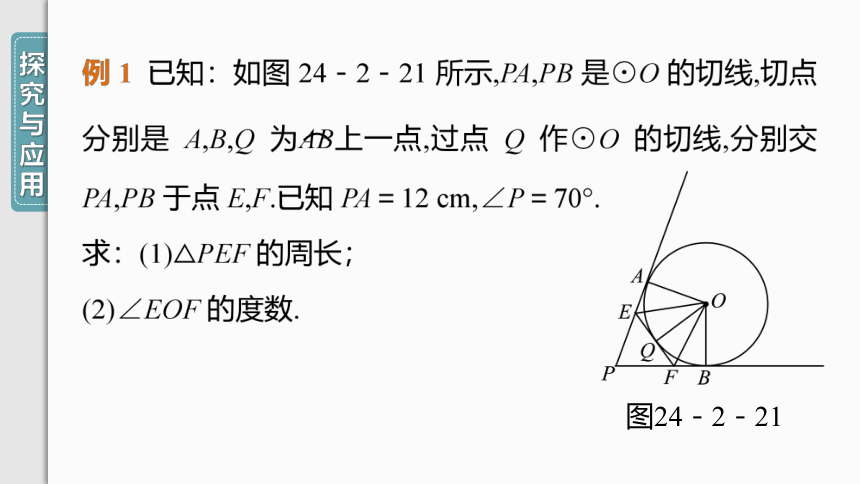
图24-2-21
解:(1)∵PA,PB,EF均是⊙O的切线,
∴PA=PB=12 cm,EA=EQ,FQ=FB,
∴△PEF的周长=PE+EQ+FQ+PF=PA+PB=12+12=24(cm).
(2)∵PA,PB,EF均是⊙O的切线,
∴PA⊥OA,PB⊥OB,EF⊥OQ,∠AEO=∠QEO,∠QFO=∠BFO,
∴∠EAO=∠EQO=90°,∠AOE=∠QOE.
同理∠BOF=∠QOF.
∵∠AOB=360°-90°-90°-∠P=110°,
切线长定理的基本图形
如图24-2-22,PA,PB为⊙O的切线,此图形中含有:
(1)一条特殊的角平分线(OP平分∠AOB,PO平分∠APB);
(2)两个等腰三角形(△PAB,△OAB);
(3)三个垂直关系(OA⊥PA,OB⊥PB,OP⊥AB).
归纳总结
图24-2-22
目标二 了解三角形的内切圆、内心的概念,会作三角形
的内切圆
思考 图24-2-23是一块三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下来的圆与三角形的三条边都相切
图24-2-23
解:如图,分别作∠ABC,∠ACB的平分线BM和CN,设它们相交于点I,那么点I到AB,BC,CA的距离都相等,以点I为圆心,点I到BC的距离ID为半径作圆,则⊙I与△ABC的三条边都相切,⊙I就是所求作的圆.
定义 与三角形各边都________的圆叫做三角形的内切圆;
内切圆的圆心是三角形________________线的交点,叫做三
角形的内心.
相切
三条角平分
例2 如图24-2-24,现有一块腰AB的长为5 dm,底边BC的长为6 dm的等腰三角形余料.求从中剪出的最大圆形盖子的面积.
[解析] 三角形的内切圆即从中剪出的最大
圆形盖子,利用三角形的面积求出内切圆的
半径,从而求出盖子的面积.
图24-2-24
解:如图,设△ABC的内切圆的圆心为O,⊙O与△ABC的三边分别相切于点D,E,F,连接OA,OB,OC,OD,OE,OF,则OD⊥BC,OE⊥AB,OF⊥AC.
由等腰三角形的“三线合一”可知A,O,D三点在同一直线上,
∵S△OAB+S△OBC+S△OAC=S△ABC,
∴AB·OE+BC·OD+AC·OF=BC·AD,
即(5+6+5)·OD=6×4,
例3 [教材P100例2]如图24-2-25,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9,BC=14,CA=13.求AF,BD,CE的长.
图24-2-25
解:设AF=x,则AE=x,
CD=CE=CA-AE=13-x,
BD=BF=AB-AF=9-x.
由BD+CD=BC,可得(13-x)+(9-x)=14,
解得x=4.
因此AF=4,BD=5,CE=9.
变式 例3中,若增加条件∠A=90°.将条件“AB=9,BC=14,CA=13”改为“AB=9,AC=12”其余条件不变,请求⊙O的半径.
解:方法一:设⊙O的半径是r.
∵∠A=90°,AB=9,AC=12,
由∠A=90°,OE,OF分别与AC,AB垂直,OE=OF,可得四边形AFOE是正方形.
∵CD=CE=12-r,BD=BF=9-r,
∴BD+CD=12-r+9-r=BC=15,
∴r=3.即⊙O的半径为3.
方法二:设⊙O的半径为r,连接OA,OB,OC.
∵∠BAC=90°,AB=9,AC=12,
又∵S△ABC=S△ABO+S△CBO+S△ACO,
∴r=3,即⊙O的半径是3.
三角形内切圆半径的求法
(3)连接内心和切点、顶点,构造直角三角形求解.
方法总结
1.三角形内切圆的圆心是( )
A.三条内角平分线的交点
B.三边垂直平分线的交点
C.三条中线的交点
D.三条高所在直线的交点
A
2.如图24-2-26,PA,PB与⊙O分别相切于点A,B,下列结论中错误的是( )
A.PA=PB
B.∠OPA=∠OPB
C.OP垂直平分AB
D.∠APB=60°
图24-2-26
D
3.如图24-2-27,PA,PB分别切⊙O于A,B两点,如果∠P=60°,PA=5,那么AB的长为________.
[解析] 由切线长定理可知PA=PB=5.
又∵∠P=60°,
∴△PAB是等边三角形,
∴AB=PA=5.
图24-2-27
5
4.如图24-2-28,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠P=40°,则∠BAC=________°.
图24-2-28
20
https://www.21cnjy.com/help/help_extract.php
24.2.2 直线和圆的位置关系
第二十四章
圆
第3课时 切线长定理和三角形的内切圆
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
1.从圆外一点可以引圆的两条切线,它们的________相等,这
一点和圆心的连线平分________________.
2.与三角形各边都________的圆叫做三角形的内切圆;内
切圆的圆心是三角形______________的交点,叫做三角形的
内心.
切线长
两条切线的夹角
相切
三条角平分线
目标一 理解切线长的概念,掌握切线长定理
探究1 过圆外一点能作几条圆的切线 请在图24-2-20中过点P画出⊙O的所有切线.
解:两条.画图如下.
图24-2-20
定义 经过圆外一点的圆的切线上,这点和________之间线
段的长,叫做这点到圆的切线长.
切点
探究2 设探究1中所画两条切线的切点分别为A,B,连接PO.
(1)依题意补全图形;
解:补全图形如下.
(2)切线长是指哪两条线段的长 这两条线段有什么关系 图中∠APO和∠BPO有什么关系 请说明理由.
解:切线长是指线段PA与PB的长;PA=PB;∠APO=∠BPO.
理由:如图,连接OA,OB.
因为PA,PB是⊙O的切线,
所以OA⊥PA,OB⊥PB.
又因为OA=OB,PO=PO,
所以Rt△AOP≌Rt△BOP,所以PA=PB,∠APO=∠BPO.
总结
切线长定理
从圆外一点可以引圆的两条切线,它们的________相等,这
一点和圆心的连线平分________________.
切线长
两条切线的夹角
图24-2-21
解:(1)∵PA,PB,EF均是⊙O的切线,
∴PA=PB=12 cm,EA=EQ,FQ=FB,
∴△PEF的周长=PE+EQ+FQ+PF=PA+PB=12+12=24(cm).
(2)∵PA,PB,EF均是⊙O的切线,
∴PA⊥OA,PB⊥OB,EF⊥OQ,∠AEO=∠QEO,∠QFO=∠BFO,
∴∠EAO=∠EQO=90°,∠AOE=∠QOE.
同理∠BOF=∠QOF.
∵∠AOB=360°-90°-90°-∠P=110°,
切线长定理的基本图形
如图24-2-22,PA,PB为⊙O的切线,此图形中含有:
(1)一条特殊的角平分线(OP平分∠AOB,PO平分∠APB);
(2)两个等腰三角形(△PAB,△OAB);
(3)三个垂直关系(OA⊥PA,OB⊥PB,OP⊥AB).
归纳总结
图24-2-22
目标二 了解三角形的内切圆、内心的概念,会作三角形
的内切圆
思考 图24-2-23是一块三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下来的圆与三角形的三条边都相切
图24-2-23
解:如图,分别作∠ABC,∠ACB的平分线BM和CN,设它们相交于点I,那么点I到AB,BC,CA的距离都相等,以点I为圆心,点I到BC的距离ID为半径作圆,则⊙I与△ABC的三条边都相切,⊙I就是所求作的圆.
定义 与三角形各边都________的圆叫做三角形的内切圆;
内切圆的圆心是三角形________________线的交点,叫做三
角形的内心.
相切
三条角平分
例2 如图24-2-24,现有一块腰AB的长为5 dm,底边BC的长为6 dm的等腰三角形余料.求从中剪出的最大圆形盖子的面积.
[解析] 三角形的内切圆即从中剪出的最大
圆形盖子,利用三角形的面积求出内切圆的
半径,从而求出盖子的面积.
图24-2-24
解:如图,设△ABC的内切圆的圆心为O,⊙O与△ABC的三边分别相切于点D,E,F,连接OA,OB,OC,OD,OE,OF,则OD⊥BC,OE⊥AB,OF⊥AC.
由等腰三角形的“三线合一”可知A,O,D三点在同一直线上,
∵S△OAB+S△OBC+S△OAC=S△ABC,
∴AB·OE+BC·OD+AC·OF=BC·AD,
即(5+6+5)·OD=6×4,
例3 [教材P100例2]如图24-2-25,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9,BC=14,CA=13.求AF,BD,CE的长.
图24-2-25
解:设AF=x,则AE=x,
CD=CE=CA-AE=13-x,
BD=BF=AB-AF=9-x.
由BD+CD=BC,可得(13-x)+(9-x)=14,
解得x=4.
因此AF=4,BD=5,CE=9.
变式 例3中,若增加条件∠A=90°.将条件“AB=9,BC=14,CA=13”改为“AB=9,AC=12”其余条件不变,请求⊙O的半径.
解:方法一:设⊙O的半径是r.
∵∠A=90°,AB=9,AC=12,
由∠A=90°,OE,OF分别与AC,AB垂直,OE=OF,可得四边形AFOE是正方形.
∵CD=CE=12-r,BD=BF=9-r,
∴BD+CD=12-r+9-r=BC=15,
∴r=3.即⊙O的半径为3.
方法二:设⊙O的半径为r,连接OA,OB,OC.
∵∠BAC=90°,AB=9,AC=12,
又∵S△ABC=S△ABO+S△CBO+S△ACO,
∴r=3,即⊙O的半径是3.
三角形内切圆半径的求法
(3)连接内心和切点、顶点,构造直角三角形求解.
方法总结
1.三角形内切圆的圆心是( )
A.三条内角平分线的交点
B.三边垂直平分线的交点
C.三条中线的交点
D.三条高所在直线的交点
A
2.如图24-2-26,PA,PB与⊙O分别相切于点A,B,下列结论中错误的是( )
A.PA=PB
B.∠OPA=∠OPB
C.OP垂直平分AB
D.∠APB=60°
图24-2-26
D
3.如图24-2-27,PA,PB分别切⊙O于A,B两点,如果∠P=60°,PA=5,那么AB的长为________.
[解析] 由切线长定理可知PA=PB=5.
又∵∠P=60°,
∴△PAB是等边三角形,
∴AB=PA=5.
图24-2-27
5
4.如图24-2-28,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠P=40°,则∠BAC=________°.
图24-2-28
20
https://www.21cnjy.com/help/help_extract.php
同课章节目录
