【人教九上数学学霸听课笔记】24.3 正多边形和圆 课件(共31张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】24.3 正多边形和圆 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 21:29:25 | ||
图片预览









文档简介
(共31张PPT)
24.3 正多边形和圆
第二十四章
圆
24.3 正多边形和圆
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
1.正多边形的________的圆心叫做正多边形的中心.
2.外接圆的________叫做正多边形的半径.
3.正多边形每一边所对的圆心角叫做正多边形的中心角,正
n边形的每个中心角都等于________.
4.中心到正多边形的一边的________叫做正多边形的边心
距.
外接圆
半径
距离
目标一 理解正多边形和圆的关系,理解正多边形的有关
概念
回顾 什么叫正多边形 正多边形的边、角有什么性质
解:各边相等,各角也相等的多边形是正多边形.性质:各边相等,各角相等.
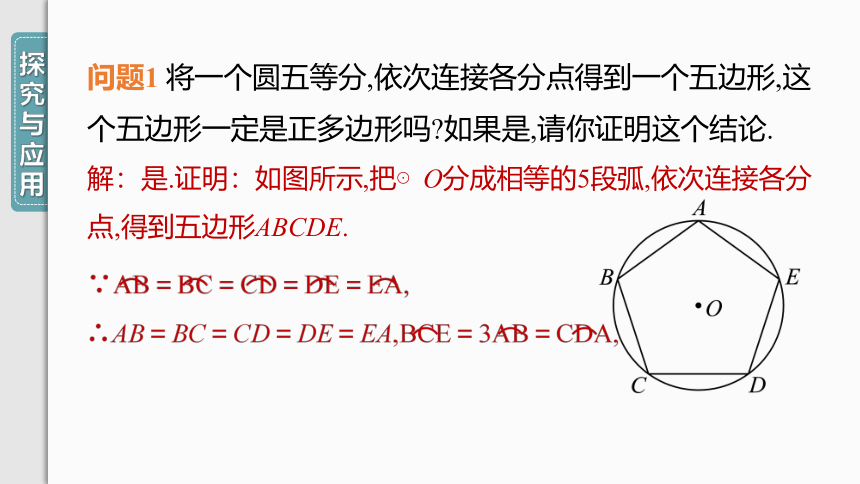
问题1 将一个圆五等分,依次连接各分点得到一个五边形,这个五边形一定是正多边形吗 如果是,请你证明这个结论.
解:是.证明:如图所示,把⊙O分成相等的5段弧,依次连接各分点,得到五边形ABCDE.
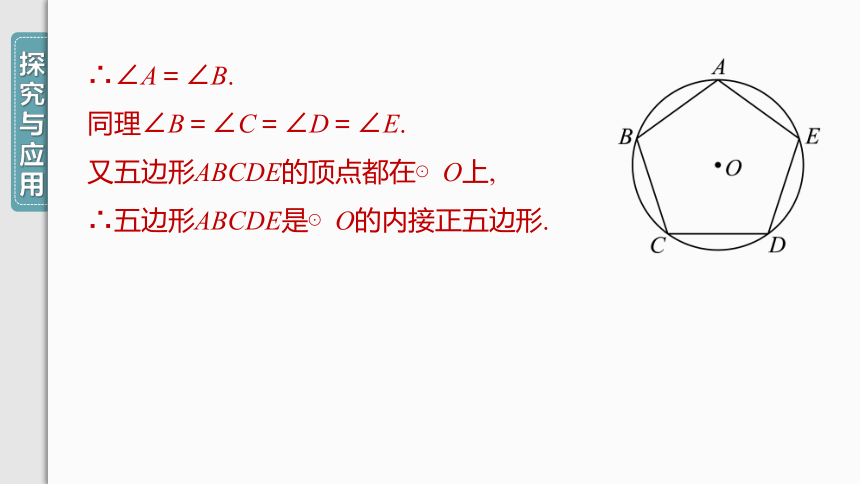
∴∠A=∠B.
同理∠B=∠C=∠D=∠E.
又五边形ABCDE的顶点都在⊙O上,
∴五边形ABCDE是⊙O的内接正五边形.
问题2 如果将一个圆n等分,依次连接各分点得到一个n边形,这个n边形一定是正n边形吗
解:这个n边形一定是正n边形.
证明方法同证明圆内接正五边形的方法.
问题3 各边相等的圆内接多边形是正多边形吗 各角相等的圆内接多边形呢 如果是,说明为什么;如果不是,举出反例.
解:各边相等的圆内接多边形是正多边形.理由如下:
∵各边相等的圆内接多边形的各角是圆周角,一定相等,
∴各边相等的圆内接多边形是正多边形.
各角相等的圆内接多边形不一定是正多边形.
反例:矩形的四个角相等,但它不是正多边形.
归纳
正多边形与圆的关系
把圆分成相等的一些弧,就可以作出这个圆的内接正多边形.
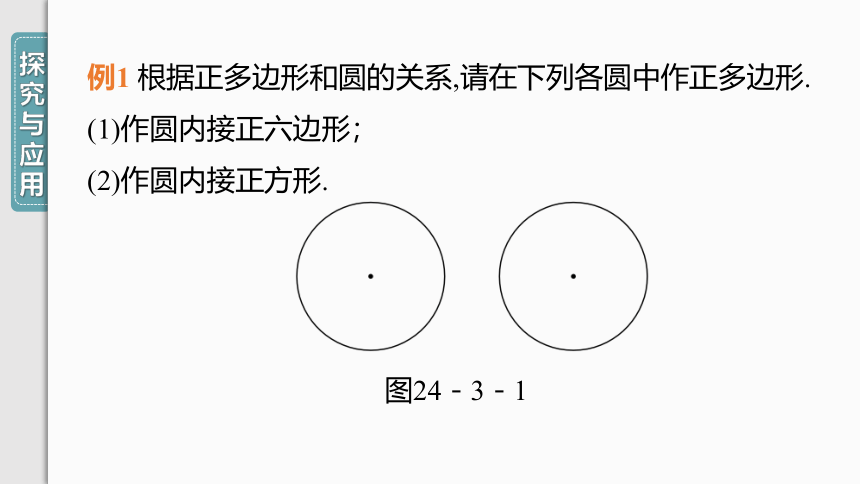
例1 根据正多边形和圆的关系,请在下列各圆中作正多边形.
(1)作圆内接正六边形;
(2)作圆内接正方形.
图24-3-1
[解析] (1)正六边形的中心角为60°,说明相邻半径和边构成的三角形是等边三角形.
(2)正方形的中心角为90°,说明相邻两条半径互相垂直.
解:画法不唯一,图略.
等分圆周画正多边形的工具和方法
(1)只用量角器:用量角器把360°的圆心角n等分,相应的圆周也被n等分,顺次连接各分点得到正n边形.
方法总结
(3)用圆规和直尺:用尺规等分圆周,可以作正六边形、正方形等特殊正多边形.
方法总结
目标二 正多边形的有关概念,会计算正多边形的边长、
半径、边心距、中心角、周长和面积
定义 如图24-3-2.
图24-3-2
1.正多边形的中心:正多边形的__________的圆心叫做正多
边形的中心.
2.正多边形的半径:外接圆的________叫做正多边形的半径.
3.正多边形的中心角:正多边形每一边所对的圆心角叫做正
多边形的中心角.正n边形的每个中心角都等于________.
4.正多边形的边心距:中心到正多边形的一边的________叫
做正多边形的边心距.
外接圆
半径
距离
例2 [教材P106例题]如图24-3-3,有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积(结果保留小数点后一位).
图24-3-3
解:如图,连接OB,OC.
因为六边形ABCDEF是正六边形,
因此,亭子地基的周长l=6×4=24(m).
作OP⊥BC,垂足为P.
变式 例2中的亭子地基如果是正八边形,其他条件不变.
(1)用适当的工具在如图24-3-4所示的圆中画出正八边形;
(2)求出地基的中心角和面积.(结果保留根号)
解:(1)如图所示.
图24-3-4
(2)如图,连接OA,OB,过点A作AM⊥OB于点M.
∴△OAM是等腰直角三角形.
正多边形计算中的基本关系式
1.与正n边形有关的角:
归纳总结
归纳总结
1.如果一个正多边形的中心角为72°,那么这个正多边形的边数是( )
A.4 B.5
C.6 D.7
B
C
B
4.正多边形的面积为240 cm2,周长是60 cm,则它的边心距是________.
8 cm
5.画半径为1 cm的圆的内接正九边形.
解:如图.(1)画半径为1 cm的圆;
(2)用量角器把⊙O九等分(依次画40°的圆心角);
(3)依次连接各分点,即得⊙O的内接正九边形ABCDEFGHI.
https://www.21cnjy.com/help/help_extract.php
24.3 正多边形和圆
第二十四章
圆
24.3 正多边形和圆
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
1.正多边形的________的圆心叫做正多边形的中心.
2.外接圆的________叫做正多边形的半径.
3.正多边形每一边所对的圆心角叫做正多边形的中心角,正
n边形的每个中心角都等于________.
4.中心到正多边形的一边的________叫做正多边形的边心
距.
外接圆
半径
距离
目标一 理解正多边形和圆的关系,理解正多边形的有关
概念
回顾 什么叫正多边形 正多边形的边、角有什么性质
解:各边相等,各角也相等的多边形是正多边形.性质:各边相等,各角相等.
问题1 将一个圆五等分,依次连接各分点得到一个五边形,这个五边形一定是正多边形吗 如果是,请你证明这个结论.
解:是.证明:如图所示,把⊙O分成相等的5段弧,依次连接各分点,得到五边形ABCDE.
∴∠A=∠B.
同理∠B=∠C=∠D=∠E.
又五边形ABCDE的顶点都在⊙O上,
∴五边形ABCDE是⊙O的内接正五边形.
问题2 如果将一个圆n等分,依次连接各分点得到一个n边形,这个n边形一定是正n边形吗
解:这个n边形一定是正n边形.
证明方法同证明圆内接正五边形的方法.
问题3 各边相等的圆内接多边形是正多边形吗 各角相等的圆内接多边形呢 如果是,说明为什么;如果不是,举出反例.
解:各边相等的圆内接多边形是正多边形.理由如下:
∵各边相等的圆内接多边形的各角是圆周角,一定相等,
∴各边相等的圆内接多边形是正多边形.
各角相等的圆内接多边形不一定是正多边形.
反例:矩形的四个角相等,但它不是正多边形.
归纳
正多边形与圆的关系
把圆分成相等的一些弧,就可以作出这个圆的内接正多边形.
例1 根据正多边形和圆的关系,请在下列各圆中作正多边形.
(1)作圆内接正六边形;
(2)作圆内接正方形.
图24-3-1
[解析] (1)正六边形的中心角为60°,说明相邻半径和边构成的三角形是等边三角形.
(2)正方形的中心角为90°,说明相邻两条半径互相垂直.
解:画法不唯一,图略.
等分圆周画正多边形的工具和方法
(1)只用量角器:用量角器把360°的圆心角n等分,相应的圆周也被n等分,顺次连接各分点得到正n边形.
方法总结
(3)用圆规和直尺:用尺规等分圆周,可以作正六边形、正方形等特殊正多边形.
方法总结
目标二 正多边形的有关概念,会计算正多边形的边长、
半径、边心距、中心角、周长和面积
定义 如图24-3-2.
图24-3-2
1.正多边形的中心:正多边形的__________的圆心叫做正多
边形的中心.
2.正多边形的半径:外接圆的________叫做正多边形的半径.
3.正多边形的中心角:正多边形每一边所对的圆心角叫做正
多边形的中心角.正n边形的每个中心角都等于________.
4.正多边形的边心距:中心到正多边形的一边的________叫
做正多边形的边心距.
外接圆
半径
距离
例2 [教材P106例题]如图24-3-3,有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积(结果保留小数点后一位).
图24-3-3
解:如图,连接OB,OC.
因为六边形ABCDEF是正六边形,
因此,亭子地基的周长l=6×4=24(m).
作OP⊥BC,垂足为P.
变式 例2中的亭子地基如果是正八边形,其他条件不变.
(1)用适当的工具在如图24-3-4所示的圆中画出正八边形;
(2)求出地基的中心角和面积.(结果保留根号)
解:(1)如图所示.
图24-3-4
(2)如图,连接OA,OB,过点A作AM⊥OB于点M.
∴△OAM是等腰直角三角形.
正多边形计算中的基本关系式
1.与正n边形有关的角:
归纳总结
归纳总结
1.如果一个正多边形的中心角为72°,那么这个正多边形的边数是( )
A.4 B.5
C.6 D.7
B
C
B
4.正多边形的面积为240 cm2,周长是60 cm,则它的边心距是________.
8 cm
5.画半径为1 cm的圆的内接正九边形.
解:如图.(1)画半径为1 cm的圆;
(2)用量角器把⊙O九等分(依次画40°的圆心角);
(3)依次连接各分点,即得⊙O的内接正九边形ABCDEFGHI.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
