【人教九上数学学霸提升作业】24.4 第1课时 弧长和扇形面积(附答案)
文档属性
| 名称 | 【人教九上数学学霸提升作业】24.4 第1课时 弧长和扇形面积(附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 21:44:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.4 第1课时 弧长和扇形面积
命题点 1 弧长公式的应用
1.[2020·南京期中] 若圆弧所在圆的半径为3,所对的圆心角为60°,则弧长为 ( )
A.π B.π C.π D.3π
2.如图24-4-1,在等边三角形ABC中,将边AC逐渐变成以BA为半径的,其他两边的长度不变,则∠ABC的度数由60°变为 ( )
图24-4-1
A.° B.° C.° D.°
3.如图24-4-2,AB为半圆O的直径,AB=4,C,D为上两点,且=.若∠CED=∠COD,则的长为 ( )
A.π B.π C.π D.π
图24-4-2 图24-4-3
4.如图24-4-3,在扇形OAB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿运动时,点D所经过的路径长为 ( )
A.3π B.π C.π D.4π
5.已知一个圆心角为270°,半径为3 m的扇形工件未搬动前如图24-4-4所示,A,B两点触地放置,搬动时,先将扇形以点B为圆心,做如图所示的无滑动翻转,再使它紧贴地面滚动,当A,B两点再次触地时停止,则圆心O所经过的路线长为 m.(结果用含π的式子表示)
图24-4-4
命题点 2 扇形面积公式的应用
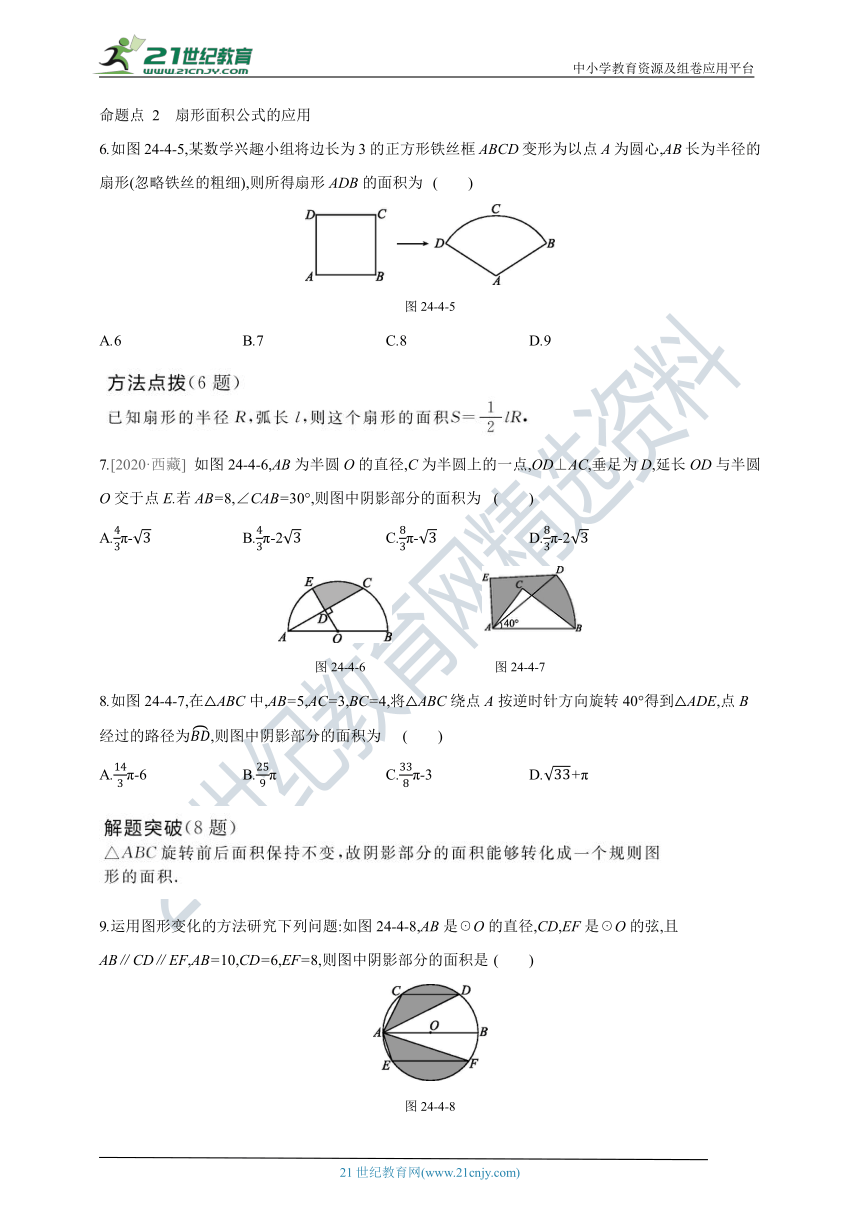
6.如图24-4-5,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以点A为圆心,AB长为半径的扇形(忽略铁丝的粗细),则所得扇形ADB的面积为 ( )
图24-4-5
A.6 B.7 C.8 D.9
7.[2020·西藏] 如图24-4-6,AB为半圆O的直径,C为半圆上的一点,OD⊥AC,垂足为D,延长OD与半圆O交于点E.若AB=8,∠CAB=30°,则图中阴影部分的面积为 ( )
A.π- B.π-2 C.π- D.π-2
图24-4-6 图24-4-7
8.如图24-4-7,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A按逆时针方向旋转40°得到△ADE,点B经过的路径为,则图中阴影部分的面积为 ( )
A.π-6 B.π C.π-3 D.+π
9.运用图形变化的方法研究下列问题:如图24-4-8,AB是☉O的直径,CD,EF是☉O的弦,且
AB∥CD∥EF,AB=10,CD=6,EF=8,则图中阴影部分的面积是 ( )
图24-4-8
A.π B.10π C.24+4π D.24+5π
10.如图24-4-9,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=6,以点C为圆心,以AC的长为半径作弧,交AB于点D,交BC于点E,则图中阴影部分的面积是 .(结果保留π)
图24-4-9 图24-4-10
11.如图24-4-10,在边长为3的正方形ABCD中,以点A为圆心,2为半径作圆弧EF,以点D为圆心,3为半径作圆弧AC.若图中阴影部分的面积分别为S1,S2,则S1-S2= .
12.如图24-4-11,已知等腰直角三角形ABC,∠ACB=90°,D是斜边AB的中点,且AC=BC=16分米,以点B为圆心,BD长为半径画弧,交BC于点F,以点C为圆心,CD长为半径画弧,与AC,BC分别交于点E,G.求阴影部分的面积.
图24-4-11
13.如图24-4-12,△ABC是等腰直角三角形,且∠ACB=90°.曲线CDEF…叫做“等腰直角三角形的渐开线”,其中,,,…的圆心依次按A,B,C,…循环.如果AC=1,那么曲线CDEF和线段CF围成图形的面积为 ( )
图24-4-12
A.π B.π C. D.
14.如图24-4-13,△ABC是正三角形,曲线CDEFG…叫做“正三角形的渐开线”,曲线的各部分为圆弧.
(1)图中已经有4段圆弧,请接着画出第5段圆弧GH.
(2)设△ABC的边长为a,则第1段弧的长是 ,第5段弧的长是 ,前5段弧长的和(即曲线CDEFGH的长)是 .
(3)类似地,有“正方形的渐开线”“正五边形的渐开线”……边长为a的正方形的渐开线的前5段弧长的和是 .
(4)猜想:①边长为a的正n边形的前5段弧长的和是 ;
②边长为a的正n边形的前m段弧长的和是 .
图24-4-13
典题讲评与答案详析
1.B
2.A [解析] 设变形后的∠B=n°,AC=的长=a.由题意可得π·a=a,解得n=.
3.D
4.C [解析] 如图,连接OD.∵D为AC的中点,AC=AO=6,∴OD⊥AC,AD=AC=AO=3,
∴∠AOD=30°,OD=3 .
作弦BF=AC,E为BF的中点,连接OE.
同理可得∠BOE=30°,
∴∠DOE=150°-60°=90°,
∴点D所经过的路径长为==π.
5.6π [解析] 由题意易知∠AOB=90°,OA=OB,
∴∠ABO=45°,圆心O旋转的长度为2×=(m),圆心O平移的距离为=(m),则圆心O经过的路线长为+=6π(m).
6.D [解析] ∵正方形的边长为3,∴的长度为6,∴S扇形ADB=lR=×6×3=9.
7.D [解析] ∵OD⊥AC,
∴∠ADO=90°,=,AD=CD,∴S△ADO=S△CDO.
∵∠CAB=30°,OA=4,∴∠COD=∠AOD=60°,
OD=OA=2,∴AD==2,
∴图中阴影部分的面积=S扇形OCE-S△CDO=S扇形OCE-S△ADO=-×2×2=-2.
故选D.
8.B [解析] 由旋转的性质得,△ADE的面积=△ABC的面积,
由图形可知,阴影部分的面积=△ADE的面积+扇形ADB的面积-△ABC的面积,
∴阴影部分的面积=扇形ADB的面积==π.
9.A [解析] 如图,作直径CG,连接OD,OE,OF,DG.
∵CG是☉O的直径,
∴∠CDG=90°,则DG==8.
又∵EF=8,∴DG=EF,
∴=,∴S扇形ODG=S扇形OEF.
∵AB∥CD∥EF,∴S△OCD=S△ACD,S△OEF=S△AEF,
∴S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆=π×52=π.
10.9-3π [解析] 如图,连接CD.
∵∠ACB=90°,∠ABC=30°,AC=6,
∴∠BAC=60°,AB=12,则BC=6.
∵CA=CD,∴△ACD是等边三角形,
∴AD=AC=6,∠ACD=60°,∴∠ECD=30°.
∵AB=12,AD=6,∴BD=6,∴AD=BD,
∴S阴影=S△ABC-S扇形CDE=××6×6-=9-3π.
故答案为9-3π.
11.-9 [解析] ∵S正方形ABCD=3×3=9,S扇形DAC=,S扇形AEF=π,
∴S1-S2=S扇形AEF-(S正方形ABCD-S扇形DAC)=π-=-9.
12.解:连接CD.∵△ABC是等腰直角三角形,D是斜边AB的中点,∴∠ACD=
∠DBF=45°,AD=BD=CD,CD⊥AB.
∵AC=BC=16,∠ACB=90°,∴AB=16,
∴BF=BD=AB=CD=8,
∴阴影部分的面积是--×-=64(分米2).
答:阴影部分的面积是64平方分米.
13.C [解析] 曲线CDEF和线段CF围成的图形是由三个圆心不同,半径不同的扇形以及△ABC组成的,所以根据面积公式可得曲线CDEF和线段CF围成图形的面积为
+×1×1=.
14.解:(1)如图.
(2)πa πa 10πa
(3)
(4)①πa ②πa
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.4 第1课时 弧长和扇形面积
命题点 1 弧长公式的应用
1.[2020·南京期中] 若圆弧所在圆的半径为3,所对的圆心角为60°,则弧长为 ( )
A.π B.π C.π D.3π
2.如图24-4-1,在等边三角形ABC中,将边AC逐渐变成以BA为半径的,其他两边的长度不变,则∠ABC的度数由60°变为 ( )
图24-4-1
A.° B.° C.° D.°
3.如图24-4-2,AB为半圆O的直径,AB=4,C,D为上两点,且=.若∠CED=∠COD,则的长为 ( )
A.π B.π C.π D.π
图24-4-2 图24-4-3
4.如图24-4-3,在扇形OAB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿运动时,点D所经过的路径长为 ( )
A.3π B.π C.π D.4π
5.已知一个圆心角为270°,半径为3 m的扇形工件未搬动前如图24-4-4所示,A,B两点触地放置,搬动时,先将扇形以点B为圆心,做如图所示的无滑动翻转,再使它紧贴地面滚动,当A,B两点再次触地时停止,则圆心O所经过的路线长为 m.(结果用含π的式子表示)
图24-4-4
命题点 2 扇形面积公式的应用
6.如图24-4-5,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以点A为圆心,AB长为半径的扇形(忽略铁丝的粗细),则所得扇形ADB的面积为 ( )
图24-4-5
A.6 B.7 C.8 D.9
7.[2020·西藏] 如图24-4-6,AB为半圆O的直径,C为半圆上的一点,OD⊥AC,垂足为D,延长OD与半圆O交于点E.若AB=8,∠CAB=30°,则图中阴影部分的面积为 ( )
A.π- B.π-2 C.π- D.π-2
图24-4-6 图24-4-7
8.如图24-4-7,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A按逆时针方向旋转40°得到△ADE,点B经过的路径为,则图中阴影部分的面积为 ( )
A.π-6 B.π C.π-3 D.+π
9.运用图形变化的方法研究下列问题:如图24-4-8,AB是☉O的直径,CD,EF是☉O的弦,且
AB∥CD∥EF,AB=10,CD=6,EF=8,则图中阴影部分的面积是 ( )
图24-4-8
A.π B.10π C.24+4π D.24+5π
10.如图24-4-9,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=6,以点C为圆心,以AC的长为半径作弧,交AB于点D,交BC于点E,则图中阴影部分的面积是 .(结果保留π)
图24-4-9 图24-4-10
11.如图24-4-10,在边长为3的正方形ABCD中,以点A为圆心,2为半径作圆弧EF,以点D为圆心,3为半径作圆弧AC.若图中阴影部分的面积分别为S1,S2,则S1-S2= .
12.如图24-4-11,已知等腰直角三角形ABC,∠ACB=90°,D是斜边AB的中点,且AC=BC=16分米,以点B为圆心,BD长为半径画弧,交BC于点F,以点C为圆心,CD长为半径画弧,与AC,BC分别交于点E,G.求阴影部分的面积.
图24-4-11
13.如图24-4-12,△ABC是等腰直角三角形,且∠ACB=90°.曲线CDEF…叫做“等腰直角三角形的渐开线”,其中,,,…的圆心依次按A,B,C,…循环.如果AC=1,那么曲线CDEF和线段CF围成图形的面积为 ( )
图24-4-12
A.π B.π C. D.
14.如图24-4-13,△ABC是正三角形,曲线CDEFG…叫做“正三角形的渐开线”,曲线的各部分为圆弧.
(1)图中已经有4段圆弧,请接着画出第5段圆弧GH.
(2)设△ABC的边长为a,则第1段弧的长是 ,第5段弧的长是 ,前5段弧长的和(即曲线CDEFGH的长)是 .
(3)类似地,有“正方形的渐开线”“正五边形的渐开线”……边长为a的正方形的渐开线的前5段弧长的和是 .
(4)猜想:①边长为a的正n边形的前5段弧长的和是 ;
②边长为a的正n边形的前m段弧长的和是 .
图24-4-13
典题讲评与答案详析
1.B
2.A [解析] 设变形后的∠B=n°,AC=的长=a.由题意可得π·a=a,解得n=.
3.D
4.C [解析] 如图,连接OD.∵D为AC的中点,AC=AO=6,∴OD⊥AC,AD=AC=AO=3,
∴∠AOD=30°,OD=3 .
作弦BF=AC,E为BF的中点,连接OE.
同理可得∠BOE=30°,
∴∠DOE=150°-60°=90°,
∴点D所经过的路径长为==π.
5.6π [解析] 由题意易知∠AOB=90°,OA=OB,
∴∠ABO=45°,圆心O旋转的长度为2×=(m),圆心O平移的距离为=(m),则圆心O经过的路线长为+=6π(m).
6.D [解析] ∵正方形的边长为3,∴的长度为6,∴S扇形ADB=lR=×6×3=9.
7.D [解析] ∵OD⊥AC,
∴∠ADO=90°,=,AD=CD,∴S△ADO=S△CDO.
∵∠CAB=30°,OA=4,∴∠COD=∠AOD=60°,
OD=OA=2,∴AD==2,
∴图中阴影部分的面积=S扇形OCE-S△CDO=S扇形OCE-S△ADO=-×2×2=-2.
故选D.
8.B [解析] 由旋转的性质得,△ADE的面积=△ABC的面积,
由图形可知,阴影部分的面积=△ADE的面积+扇形ADB的面积-△ABC的面积,
∴阴影部分的面积=扇形ADB的面积==π.
9.A [解析] 如图,作直径CG,连接OD,OE,OF,DG.
∵CG是☉O的直径,
∴∠CDG=90°,则DG==8.
又∵EF=8,∴DG=EF,
∴=,∴S扇形ODG=S扇形OEF.
∵AB∥CD∥EF,∴S△OCD=S△ACD,S△OEF=S△AEF,
∴S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆=π×52=π.
10.9-3π [解析] 如图,连接CD.
∵∠ACB=90°,∠ABC=30°,AC=6,
∴∠BAC=60°,AB=12,则BC=6.
∵CA=CD,∴△ACD是等边三角形,
∴AD=AC=6,∠ACD=60°,∴∠ECD=30°.
∵AB=12,AD=6,∴BD=6,∴AD=BD,
∴S阴影=S△ABC-S扇形CDE=××6×6-=9-3π.
故答案为9-3π.
11.-9 [解析] ∵S正方形ABCD=3×3=9,S扇形DAC=,S扇形AEF=π,
∴S1-S2=S扇形AEF-(S正方形ABCD-S扇形DAC)=π-=-9.
12.解:连接CD.∵△ABC是等腰直角三角形,D是斜边AB的中点,∴∠ACD=
∠DBF=45°,AD=BD=CD,CD⊥AB.
∵AC=BC=16,∠ACB=90°,∴AB=16,
∴BF=BD=AB=CD=8,
∴阴影部分的面积是--×-=64(分米2).
答:阴影部分的面积是64平方分米.
13.C [解析] 曲线CDEF和线段CF围成的图形是由三个圆心不同,半径不同的扇形以及△ABC组成的,所以根据面积公式可得曲线CDEF和线段CF围成图形的面积为
+×1×1=.
14.解:(1)如图.
(2)πa πa 10πa
(3)
(4)①πa ②πa
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
