【人教九上数学学霸听课笔记】24.4 第1课时 弧长和扇形面积 课件(共31张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】24.4 第1课时 弧长和扇形面积 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 21:28:44 | ||
图片预览









文档简介
(共31张PPT)
24.4 弧长和扇形面积
第二十四章
圆
第1课时 弧长和扇形面积
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
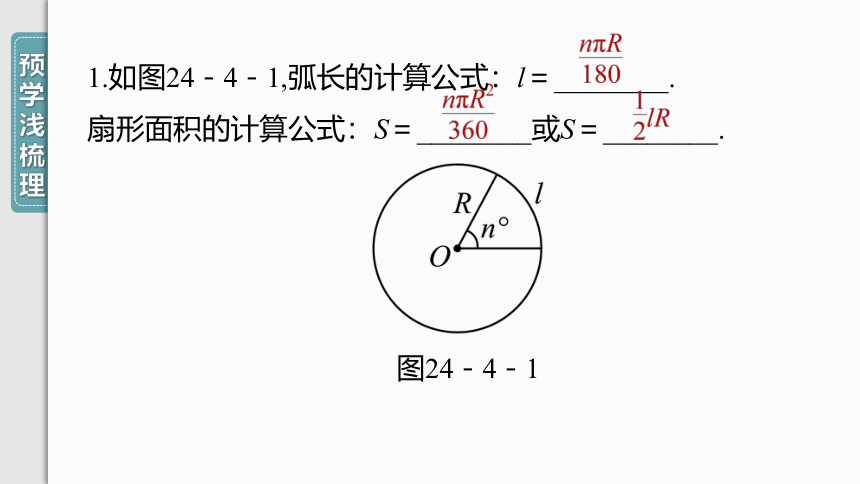
1.如图24-4-1,弧长的计算公式:l=________.
扇形面积的计算公式:S=________或S=________.
图24-4-1
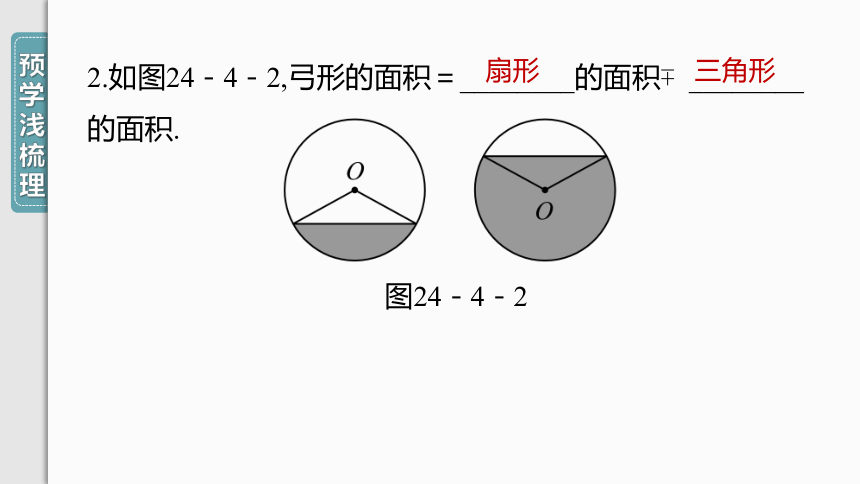
2.如图24-4-2,弓形的面积=________的面积 ________的面积.
图24-4-2
扇形
三角形
目标一 能推导弧长计算公式,并能运用其计算弧长
问题 弧是圆的一部分,那么弧长就是圆周长的一部分,如果一个圆的半径为r,如何计算n°的圆心角所对的弧长呢
探究 (1)圆的周长如何计算
(2)圆的周长可以看作是多少度的圆心角所对的弧长
(3)1°的圆心角所对的弧长是多少 n°的圆心角呢
(4)由上面的问题可知,弧长的大小由哪些量决定
解:(1)圆的周长C=2πr.(2)360°.
(4)弧长的大小由圆的半径和弧所对的圆心角决定.
练习 在半径为4的圆中,120°的圆心角所对的弧的长度是________.
练习 若扇形的半径为5 cm,弧长为8π cm,则扇形的圆心角是__________.
288°
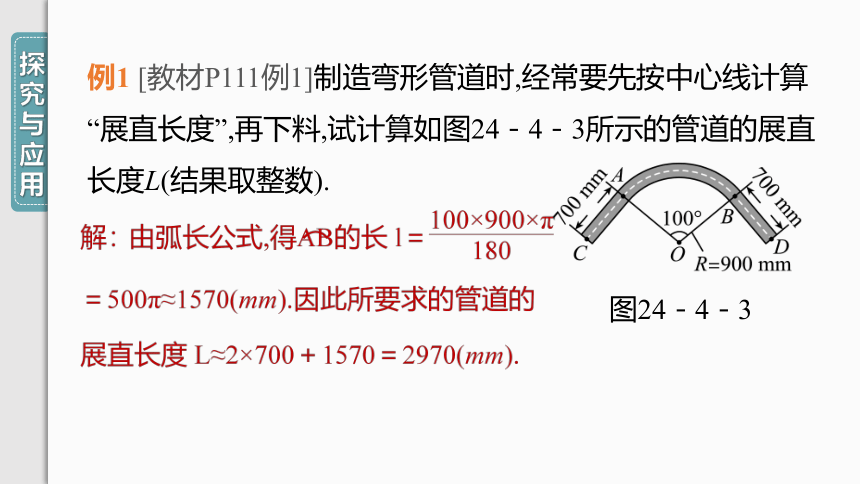
例1 [教材P111例1]制造弯形管道时,经常要先按中心线计算“展直长度”,再下料,试计算如图24-4-3所示的管道的展直长度L(结果取整数).
图24-4-3
图J24-4-1
∴AO=BO,∠OAB=∠OBA=150°-90°=60°,
∴△AOB为等边三角形,
∴AO=BO=AB=180 m,∠AOB=60°,
即点A到点B这段弧形公路的长为60π m.
目标二 能推导扇形的面积计算公式,并能运用其计算扇
形的面积
定义 由组成圆心角的__________和圆心角所对的
___________图形叫做扇形.
两条半径
弧围成的
思考 1.由扇形的定义可知,扇形面积就是________的一部分.如果一个扇形的半径为r,圆心角为n°,请仿照弧长公式的推导过程推导扇形面积的计算公式.
解:在半径为r的圆中,因为圆的面积为πr2,
圆面积
2.观察得出的扇形面积公式与弧长公式,扇形与它相应的弧长之间有什么关系 请推导并写出用弧长表示扇形面积的关系式.
练习 已知扇形的圆心角为60°,半径为3 cm,则这个扇形的面积为________cm2.
练习1 已知扇形的半径为12,弧长为4π,则该扇形的面积是________.
练习2 一个扇形的圆心角为120°,它的面积是12π cm2,则这个扇形的弧长为_______ cm.
24π
4π
例2 [教材P112例2]如图24-4-4,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高0.3 m,求截面上有水部分的面积(结果保留小数点后两位).
图24-4-4
∵OC=0.6 m,DC=0.3 m,
∴OD=OC-DC=0.3(m),
∴OD=DC.
又AD⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC,
∴△AOC是等边三角形,
∴∠AOD=60°,
∴∠AOB=120°.
变式 如图24-4-5所示,△ABC内接于⊙O,∠B=60°,⊙O的半径为2 cm,求阴影部分的面积.
图24-4-5
∵∠B=60°,
∴∠AOC=120°.
又∵OA=OC,
∴∠OAC=∠OCA=30°.
∵在Rt△AOE中,OA=2 cm,
∴OE=1 cm,
1.扇形面积公式的选择
归纳总结
2.弓形面积的求法
如图24-4-6,若弓形AMB的面积小于半圆的面积,则S弓形=S扇形OAB-S△OAB;
若弓形AMB的面积大于半圆的面积,则S弓形=S扇形OAB+S△OAB.
归纳总结
图24-4-6
B
50°
3.已知扇形的圆心角为120°,弧长为6π,则扇形的面积是________.
27π
4.如图24-4-7,已知C,D是以AB为直径的半圆上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于________.
图24-4-7
https://www.21cnjy.com/help/help_extract.php
24.4 弧长和扇形面积
第二十四章
圆
第1课时 弧长和扇形面积
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
1.如图24-4-1,弧长的计算公式:l=________.
扇形面积的计算公式:S=________或S=________.
图24-4-1
2.如图24-4-2,弓形的面积=________的面积 ________的面积.
图24-4-2
扇形
三角形
目标一 能推导弧长计算公式,并能运用其计算弧长
问题 弧是圆的一部分,那么弧长就是圆周长的一部分,如果一个圆的半径为r,如何计算n°的圆心角所对的弧长呢
探究 (1)圆的周长如何计算
(2)圆的周长可以看作是多少度的圆心角所对的弧长
(3)1°的圆心角所对的弧长是多少 n°的圆心角呢
(4)由上面的问题可知,弧长的大小由哪些量决定
解:(1)圆的周长C=2πr.(2)360°.
(4)弧长的大小由圆的半径和弧所对的圆心角决定.
练习 在半径为4的圆中,120°的圆心角所对的弧的长度是________.
练习 若扇形的半径为5 cm,弧长为8π cm,则扇形的圆心角是__________.
288°
例1 [教材P111例1]制造弯形管道时,经常要先按中心线计算“展直长度”,再下料,试计算如图24-4-3所示的管道的展直长度L(结果取整数).
图24-4-3
图J24-4-1
∴AO=BO,∠OAB=∠OBA=150°-90°=60°,
∴△AOB为等边三角形,
∴AO=BO=AB=180 m,∠AOB=60°,
即点A到点B这段弧形公路的长为60π m.
目标二 能推导扇形的面积计算公式,并能运用其计算扇
形的面积
定义 由组成圆心角的__________和圆心角所对的
___________图形叫做扇形.
两条半径
弧围成的
思考 1.由扇形的定义可知,扇形面积就是________的一部分.如果一个扇形的半径为r,圆心角为n°,请仿照弧长公式的推导过程推导扇形面积的计算公式.
解:在半径为r的圆中,因为圆的面积为πr2,
圆面积
2.观察得出的扇形面积公式与弧长公式,扇形与它相应的弧长之间有什么关系 请推导并写出用弧长表示扇形面积的关系式.
练习 已知扇形的圆心角为60°,半径为3 cm,则这个扇形的面积为________cm2.
练习1 已知扇形的半径为12,弧长为4π,则该扇形的面积是________.
练习2 一个扇形的圆心角为120°,它的面积是12π cm2,则这个扇形的弧长为_______ cm.
24π
4π
例2 [教材P112例2]如图24-4-4,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高0.3 m,求截面上有水部分的面积(结果保留小数点后两位).
图24-4-4
∵OC=0.6 m,DC=0.3 m,
∴OD=OC-DC=0.3(m),
∴OD=DC.
又AD⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC,
∴△AOC是等边三角形,
∴∠AOD=60°,
∴∠AOB=120°.
变式 如图24-4-5所示,△ABC内接于⊙O,∠B=60°,⊙O的半径为2 cm,求阴影部分的面积.
图24-4-5
∵∠B=60°,
∴∠AOC=120°.
又∵OA=OC,
∴∠OAC=∠OCA=30°.
∵在Rt△AOE中,OA=2 cm,
∴OE=1 cm,
1.扇形面积公式的选择
归纳总结
2.弓形面积的求法
如图24-4-6,若弓形AMB的面积小于半圆的面积,则S弓形=S扇形OAB-S△OAB;
若弓形AMB的面积大于半圆的面积,则S弓形=S扇形OAB+S△OAB.
归纳总结
图24-4-6
B
50°
3.已知扇形的圆心角为120°,弧长为6π,则扇形的面积是________.
27π
4.如图24-4-7,已知C,D是以AB为直径的半圆上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于________.
图24-4-7
https://www.21cnjy.com/help/help_extract.php
同课章节目录
