【人教九上数学学霸听课笔记】24.4 第2课时 圆锥的侧面积和全面积 课件(共28张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】24.4 第2课时 圆锥的侧面积和全面积 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 21:28:01 | ||
图片预览





文档简介
(共26张PPT)
24.4 弧长和扇形面积
第二十四章
圆
第2课时 圆锥的侧面积和全面积
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
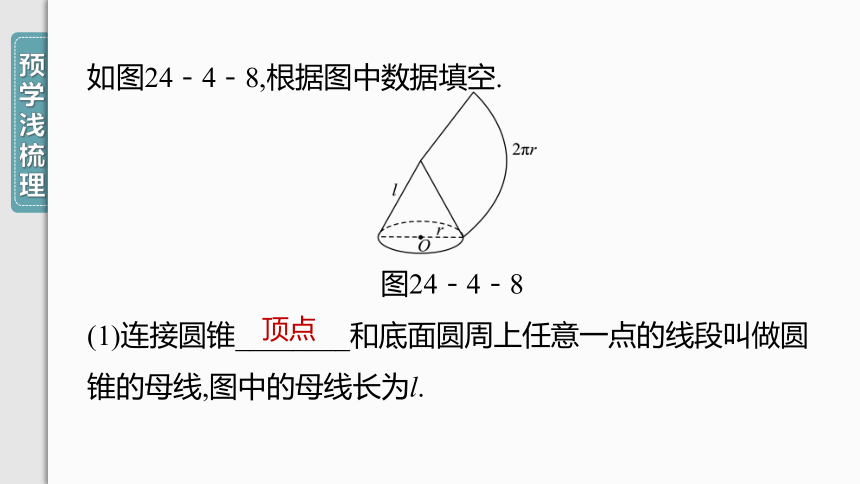
如图24-4-8,根据图中数据填空.
图24-4-8
(1)连接圆锥________和底面圆周上任意一点的线段叫做圆锥的母线,图中的母线长为l.
顶点
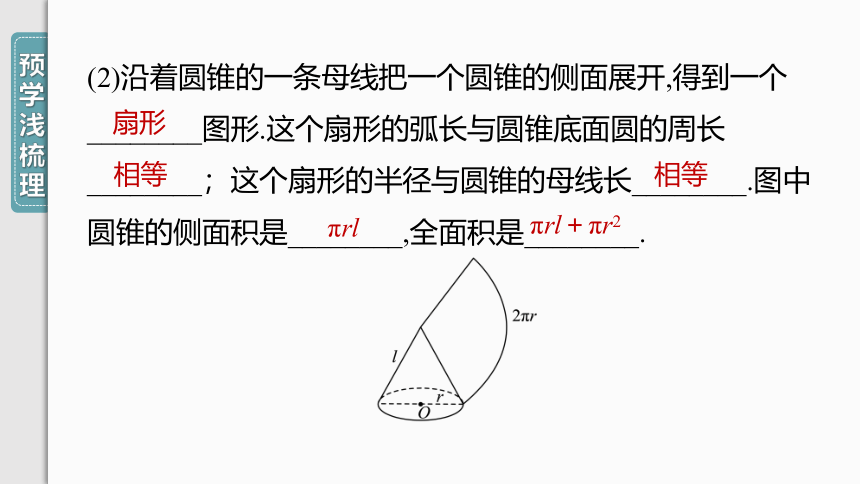
(2)沿着圆锥的一条母线把一个圆锥的侧面展开,得到一个________图形.这个扇形的弧长与圆锥底面圆的周长________;这个扇形的半径与圆锥的母线长________.图中圆锥的侧面积是________,全面积是________.
扇形
相等
相等
πrl
πrl+πr2
目标一 了解圆锥及其母线、侧面积、全面积等概念,会
计算圆锥的侧面积和全面积
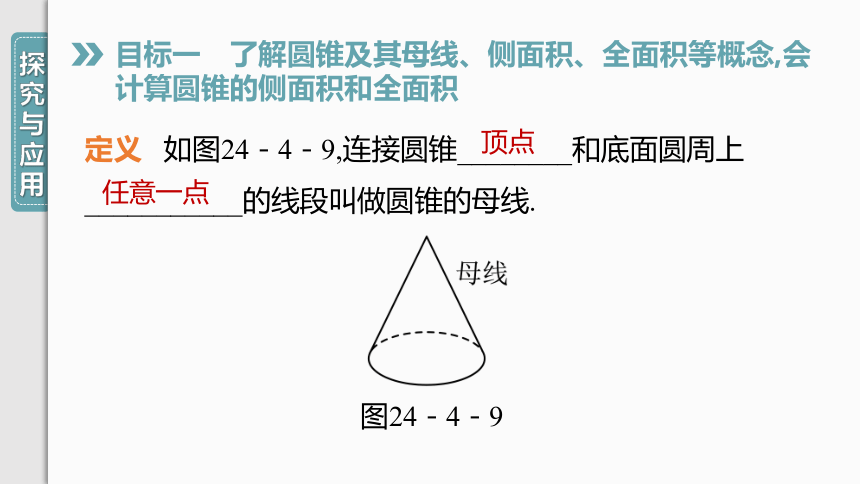
定义 如图24-4-9,连接圆锥________和底面圆周上___________的线段叫做圆锥的母线.
图24-4-9
顶点
任意一点
思考 1.圆锥有多少条母线
解:无数条.
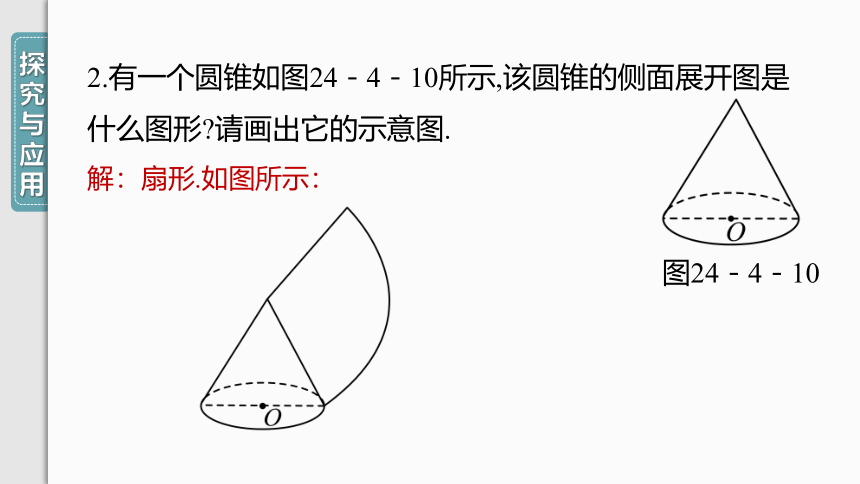
2.有一个圆锥如图24-4-10所示,该圆锥的侧面展开图是什么图形 请画出它的示意图.
解:扇形.如图所示:
图24-4-10
3.观察第2题中画出的图形,圆锥的母线与展开图的半径有什么关系 圆锥的底面圆周长与展开图的弧长有什么关系
解:相等.相等.
4.如果该圆锥的母线长为l,底面圆半径为r,如何计算圆锥的侧面积、全面积
解:如图所示,圆锥的侧面展开图是一个扇形.
∵圆锥的底面圆周长与展开图的弧长相等,得扇形的弧长为2πr,
∴圆锥的全面积=πrl+πr2=πr(r+l).
练习1 一个圆锥的母线长为4 cm,底面圆的半径为3 cm,则这个圆锥的侧面积是________ cm2.
练习2 一个圆锥的底面圆半径是3 cm,母线长是12 cm,若将该圆锥的侧面沿着母线剪开得到一个扇形,则该扇形的圆心角的度数是________.
12π
90°
练习 一张扇形纸片,半径是6,圆心角为120°,将它围成一个圆锥,则这个圆锥的底面圆半径为_______.
2
求圆锥侧面积的“三个公式”
归纳总结
(3)已知圆锥底面圆的半径r和母线长l,一般用公式S侧=πrl.
目标二 圆锥的展开图的应用
例1 根据下列条件求值(如图24-4-11,其中r,h,a分别是圆锥的底面圆半径、高线、母线长).
(1)若a=2,r=1,则h=________;
(2)若a=10,h=8,则r=________.
图24-4-11
6
例2 [教材P114例3]蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建20个底面积为12 m2,高为3.2 m,外围高1.8 m的蒙古包,至少需要多少平方米的毛毡(π取3.142,结果取整数)
图24-4-12
解:如图是一个蒙古包的示意图.
根据题意,下部圆柱的底面积为12 m2,高h2=
1.8 m;上部圆锥的高h1=3.2-1.8=1.4(m).
侧面积为2π×1.954×1.8≈22.10(m2).
侧面展开扇形的弧长为2π×1.954≈12.28(m),
因此,搭建20个这样的蒙古包至少需要毛毡20×(22.10+14.76)≈738(m2).
例 如图J24-4-2所示,在Rt△ABC中,∠C=90°,AB=13 cm,
BC=5 cm,求以AB为轴旋转一周所得到的几何体的全面积.
解:如图,过点C作CD⊥AB,
垂足为D.
图J24-4-2
计算圆锥全面积的“四个关键点”
1.分析清楚圆锥表面的构成;
2.弄清圆锥与其侧面展开图(扇形)各元素之间的对应关系;
3.圆锥的母线长l、底面圆的半径r和圆锥的高h的关系为l2
=r2+h2;
4.圆锥的全面积等于其侧面积与底面积的和.
归纳总结
1.已知圆锥形模具的母线长是12 cm,底面圆的半径是4 cm,则这个模具的侧面积是( )
A.100π cm2 B.80π cm2
C.60π cm2 D.48π cm2
D
图24-4-13
A
3.将圆心角为90°,面积为4π cm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面圆半径为( )
A.1 cm B.2 cm
C.3 cm D.4 cm
A
图24-4-14
D
5.将一个底面圆半径为6 cm,母线长为15 cm的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是________度.
144
24.4 弧长和扇形面积
第二十四章
圆
第2课时 圆锥的侧面积和全面积
预学浅梳理 探究与应用 随堂小检测
第二十四章 圆
如图24-4-8,根据图中数据填空.
图24-4-8
(1)连接圆锥________和底面圆周上任意一点的线段叫做圆锥的母线,图中的母线长为l.
顶点
(2)沿着圆锥的一条母线把一个圆锥的侧面展开,得到一个________图形.这个扇形的弧长与圆锥底面圆的周长________;这个扇形的半径与圆锥的母线长________.图中圆锥的侧面积是________,全面积是________.
扇形
相等
相等
πrl
πrl+πr2
目标一 了解圆锥及其母线、侧面积、全面积等概念,会
计算圆锥的侧面积和全面积
定义 如图24-4-9,连接圆锥________和底面圆周上___________的线段叫做圆锥的母线.
图24-4-9
顶点
任意一点
思考 1.圆锥有多少条母线
解:无数条.
2.有一个圆锥如图24-4-10所示,该圆锥的侧面展开图是什么图形 请画出它的示意图.
解:扇形.如图所示:
图24-4-10
3.观察第2题中画出的图形,圆锥的母线与展开图的半径有什么关系 圆锥的底面圆周长与展开图的弧长有什么关系
解:相等.相等.
4.如果该圆锥的母线长为l,底面圆半径为r,如何计算圆锥的侧面积、全面积
解:如图所示,圆锥的侧面展开图是一个扇形.
∵圆锥的底面圆周长与展开图的弧长相等,得扇形的弧长为2πr,
∴圆锥的全面积=πrl+πr2=πr(r+l).
练习1 一个圆锥的母线长为4 cm,底面圆的半径为3 cm,则这个圆锥的侧面积是________ cm2.
练习2 一个圆锥的底面圆半径是3 cm,母线长是12 cm,若将该圆锥的侧面沿着母线剪开得到一个扇形,则该扇形的圆心角的度数是________.
12π
90°
练习 一张扇形纸片,半径是6,圆心角为120°,将它围成一个圆锥,则这个圆锥的底面圆半径为_______.
2
求圆锥侧面积的“三个公式”
归纳总结
(3)已知圆锥底面圆的半径r和母线长l,一般用公式S侧=πrl.
目标二 圆锥的展开图的应用
例1 根据下列条件求值(如图24-4-11,其中r,h,a分别是圆锥的底面圆半径、高线、母线长).
(1)若a=2,r=1,则h=________;
(2)若a=10,h=8,则r=________.
图24-4-11
6
例2 [教材P114例3]蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建20个底面积为12 m2,高为3.2 m,外围高1.8 m的蒙古包,至少需要多少平方米的毛毡(π取3.142,结果取整数)
图24-4-12
解:如图是一个蒙古包的示意图.
根据题意,下部圆柱的底面积为12 m2,高h2=
1.8 m;上部圆锥的高h1=3.2-1.8=1.4(m).
侧面积为2π×1.954×1.8≈22.10(m2).
侧面展开扇形的弧长为2π×1.954≈12.28(m),
因此,搭建20个这样的蒙古包至少需要毛毡20×(22.10+14.76)≈738(m2).
例 如图J24-4-2所示,在Rt△ABC中,∠C=90°,AB=13 cm,
BC=5 cm,求以AB为轴旋转一周所得到的几何体的全面积.
解:如图,过点C作CD⊥AB,
垂足为D.
图J24-4-2
计算圆锥全面积的“四个关键点”
1.分析清楚圆锥表面的构成;
2.弄清圆锥与其侧面展开图(扇形)各元素之间的对应关系;
3.圆锥的母线长l、底面圆的半径r和圆锥的高h的关系为l2
=r2+h2;
4.圆锥的全面积等于其侧面积与底面积的和.
归纳总结
1.已知圆锥形模具的母线长是12 cm,底面圆的半径是4 cm,则这个模具的侧面积是( )
A.100π cm2 B.80π cm2
C.60π cm2 D.48π cm2
D
图24-4-13
A
3.将圆心角为90°,面积为4π cm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面圆半径为( )
A.1 cm B.2 cm
C.3 cm D.4 cm
A
图24-4-14
D
5.将一个底面圆半径为6 cm,母线长为15 cm的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是________度.
144
同课章节目录
