【人教九上数学学霸提升作业】24.4 第二十四章 圆 中考特训(四) 圆(附答案)
文档属性
| 名称 | 【人教九上数学学霸提升作业】24.4 第二十四章 圆 中考特训(四) 圆(附答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 21:56:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考特训(四) 圆
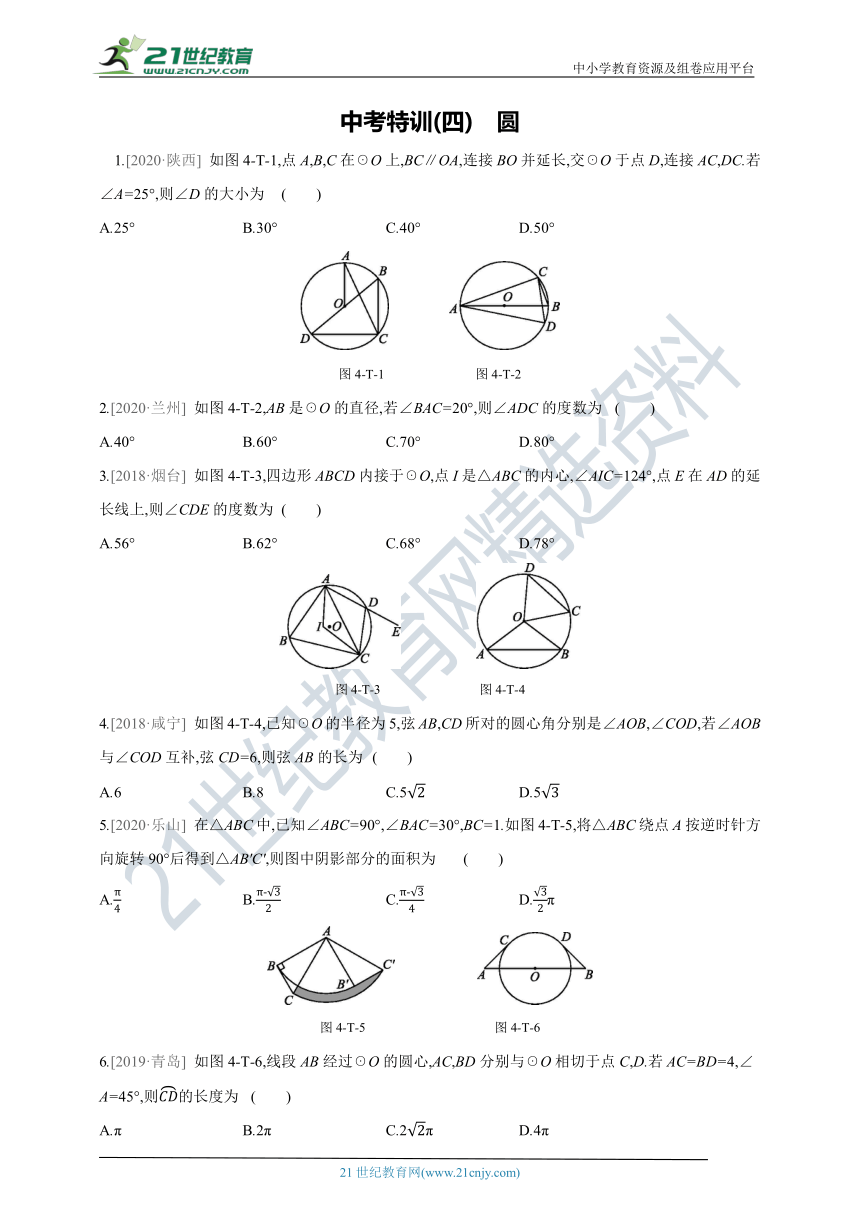
1.[2020·陕西] 如图4-T-1,点A,B,C在☉O上,BC∥OA,连接BO并延长,交☉O于点D,连接AC,DC.若∠A=25°,则∠D的大小为 ( )
A.25° B.30° C.40° D.50°
图4-T-1 图4-T-2
2.[2020·兰州] 如图4-T-2,AB是☉O的直径,若∠BAC=20°,则∠ADC的度数为 ( )
A.40° B.60° C.70° D.80°
3.[2018·烟台] 如图4-T-3,四边形ABCD内接于☉O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为 ( )
A.56° B.62° C.68° D.78°
图4-T-3 图4-T-4
4.[2018·咸宁] 如图4-T-4,已知☉O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为 ( )
A.6 B.8 C.5 D.5
5.[2020·乐山] 在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图4-T-5,将△ABC绕点A按逆时针方向旋转90°后得到△AB'C',则图中阴影部分的面积为 ( )
A. B. C. D.π
图4-T-5 图4-T-6
6.[2019·青岛] 如图4-T-6,线段AB经过☉O的圆心,AC,BD分别与☉O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为 ( )
A.π B.2π C.2π D.4π
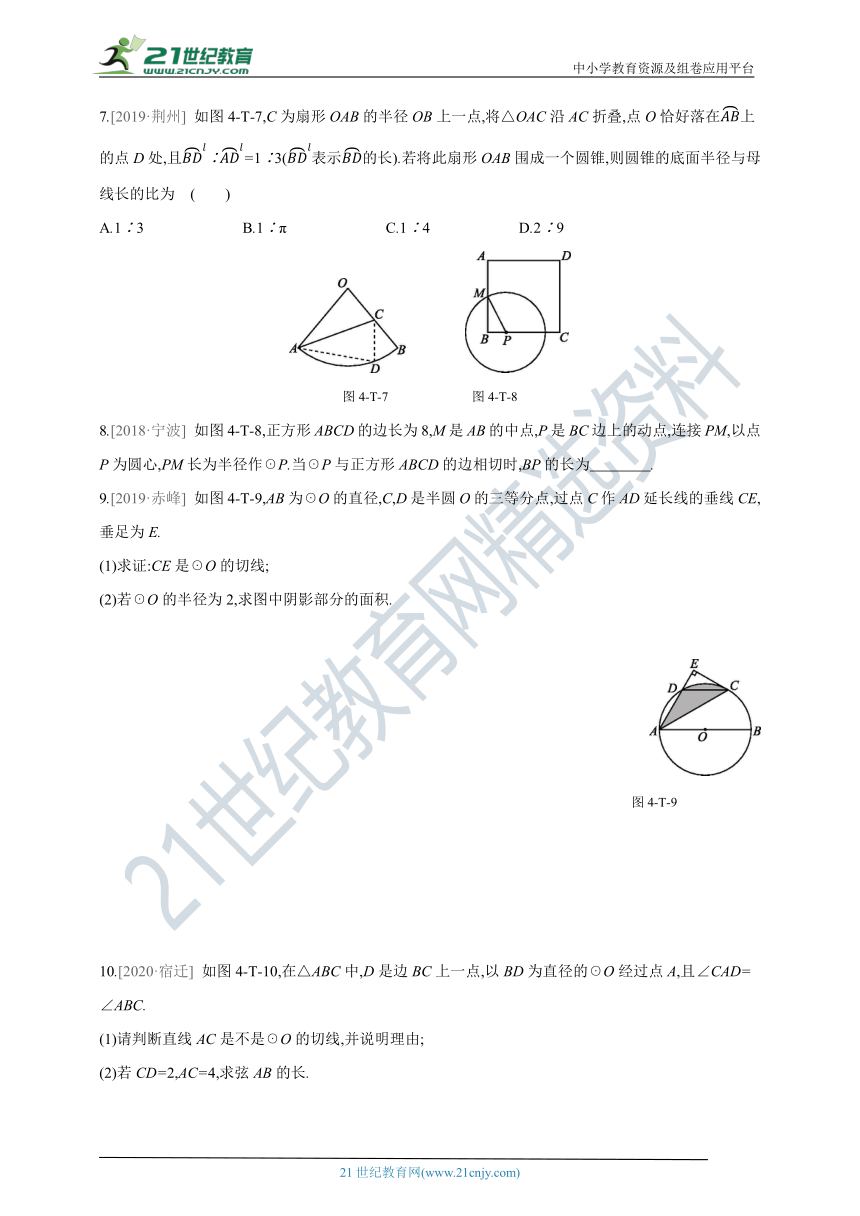
7.[2019·荆州] 如图4-T-7,C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在上的点D处,且∶=1∶3(表示的长).若将此扇形OAB围成一个圆锥,则圆锥的底面半径与母线长的比为 ( )
A.1∶3 B.1∶π C.1∶4 D.2∶9
图4-T-7 图4-T-8
8.[2018·宁波] 如图4-T-8,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作☉P.当☉P与正方形ABCD的边相切时,BP的长为 .
9.[2019·赤峰] 如图4-T-9,AB为☉O的直径,C,D是半圆O的三等分点,过点C作AD延长线的垂线CE,垂足为E.
(1)求证:CE是☉O的切线;
(2)若☉O的半径为2,求图中阴影部分的面积.
图4-T-9
10.[2020·宿迁] 如图4-T-10,在△ABC中,D是边BC上一点,以BD为直径的☉O经过点A,且∠CAD=∠ABC.
(1)请判断直线AC是不是☉O的切线,并说明理由;
(2)若CD=2,AC=4,求弦AB的长.
图4-T-10
11.[2018·天津] 如图4-T-11,已知AB是☉O的直径,弦CD与AB相交,∠BAC=38°.
(1)如图①,若D为的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作☉O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
图4-T-11
12.[2018·北京] 对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离”,记作d(M,N).已知点A(-2,6),B(-2,-2),C(6,-2).
(1)求d(点O,△ABC);
(2)记函数y=kx(-1≤x≤1,k≠0)的图象为图形G.若d(G,△ABC)=1,直接写出k的取值范围;
(3)☉T的圆心为T(t,0),半径为1.若d(☉T,△ABC)=1,直接写出t的取值范围.
典题讲评与答案详析
1.C [解析] ∵BC∥OA,
∴∠ACB=∠A=25°,
∴∠B=∠AOB=2∠ACB=50°.
∵BD是☉O的直径,∴∠BCD=90°,
∴∠D=90°-∠B=90°-50°=40°.
故选C.
2.C [解析] ∵AB是☉O的直径,∴∠ACB=90°.
∵∠BAC=20°,∴∠ABC=90°-20°=70°,
∴∠ADC=∠ABC=70°.
故选C.
3.C [解析] ∵点I是△ABC的内心,
∴∠BAC=2∠IAC,∠ACB=2∠ICA.
∵∠AIC=124°,
∴∠B=180°-(∠BAC+∠ACB)=180°-2(∠IAC+∠ICA)=180°-2(180°-∠AIC)=68°.
又四边形ABCD内接于☉O,
∴∠CDE=∠B=68°.
4.B [解析] 如图,延长AO交☉O于点E,连接BE,
则∠AOB+∠BOE=180°.
又∵∠AOB+∠COD=180°,
∴∠BOE=∠COD,
∴BE=CD=6.
∵AE为☉O的直径,∴∠ABE=90°,
∴AB==8.
5.B [解析] ∵∠ABC=90°,∠BAC=30°,BC=1,
∴AC=2BC=2,∴AB==,
∴图中阴影部分的面积=--××1=.
6.B 7.D
8.3或4 [解析] ∵正方形ABCD的边长为8,M是AB的中点,∴BM=AB=4.
如图①,当☉P与CD边相切时,设PC=PM=x.
在Rt△PBM中,
∵PM2=BM2+BP2,∴x2=42+(8-x)2,
∴x=5,∴BP=8-x=8-5=3.
如图②,当☉P与AD边相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形,
∴PM=PK=CD=8.
又∵BM=4,
∴BP==4.
综上所述,BP的长为3或4.
9.解:(1)证明:连接OC.
∵C,D为半圆O的三等分点,
∴==,∴∠DAC=∠BAC.
∵OA=OC,∴∠BAC=∠ACO,
∴∠DAC=∠ACO,∴OC∥AD.
∵CE⊥AD,∴CE⊥OC.
又∵OC是☉O的半径,∴CE是☉O的切线.
(2)连接OD.
∵==,
∴∠AOD=∠COD=∠BOC=×180°=60°.
又∵OC=OD,
∴△COD为等边三角形,
∴∠CDO=60°=∠AOD,
∴CD∥AB,∴S△ACD=S△COD,
∴图中阴影部分的面积=S扇形OCD==.
10.解:(1)直线AC是☉O的切线.
理由如下:如图,连接OA.
∵BD为☉O的直径,
∴∠BAD=90°=∠OAB+∠OAD.
∵OA=OB,∴∠OAB=∠ABC.
又∵∠CAD=∠ABC,
∴∠OAB=∠ABC=∠CAD,
∴∠OAD+∠CAD=∠OAD+∠OAB=90°=∠OAC,
∴AC⊥OA.
又∵OA是☉O的半径,
∴直线AC是☉O的切线.
(2)如图,过点A作AE⊥BD于点E,
∴∠AEC=∠AEB=90°.
由(1)知∠OAC=90°,
∴在Rt△OAC中,OC2=AC2+OA2,
∴(OA+2)2=16+OA2,
∴OA=3,∴OC=5,BC=8.
∵S△OAC=OA·AC=OC·AE,
∴AE==,
∴OE===,
∴BE=OB+OE=,
∴AB===.
11.解:(1)如图①,连接OD.
∵AB是☉O的直径,∴∠ACB=90°,
∴∠ABC=90°-∠BAC=90°-38°=52°.
∵D为的中点,∠AOB=180°,
∴∠AOD=90°,∴∠ABD=∠AOD=45°.
(2)如图②,连接OD.
∵DP切☉O于点D,
∴OD⊥DP,即∠ODP=90°.
∵DP∥AC,∠BAC=38°,∴∠P=∠BAC=38°.
∵∠AOD是△ODP的一个外角,
∴∠AOD=∠P+∠ODP=128°,
∴∠ACD=64°.
∵OC=OA,∠BAC=38°,
∴∠OCA=∠BAC=38°,
∴∠OCD=∠ACD-∠OCA=64°-38°=26°.
12.解:(1)如图所示,点O到△ABC的距离的最小值为2,
∴d(点O,△ABC)=2.
(2)如图,函数y=kx(k≠0)的图象经过原点,
在-1≤x≤1范围内,函数图象为线段.
当函数y=kx(-1≤x≤1,k≠0)的图象经过点(1,-1)时,k=-1,此时d(G,△ABC)=1;
当函数y=kx(-1≤x≤1,k≠0)的图象经过点(-1,-1)时,k=1,此时d(G,△ABC)=1.
∴-1≤k≤1.
又∵k≠0,∴-1≤k≤1且k≠0.
(3)如图,☉T与△ABC的位置关系分三种情况:
①当☉T在△ABC的左侧时,d(☉T,△ABC)=1,此时t=-4.
②当☉T在△ABC的内部时,
当点T与原点重合时,d(☉T,△ABC)=1,
此时t=0;
当点T位于T3位置时,由d(☉T,△ABC)=1知T3M=2.
∵AB=BC=8,∠ABC=90°,
∴∠C=∠T3DM=45°,
则T3D=2,
∴t=4-2.
故此时0≤t≤4-2.
③当☉T在△ABC的右侧时,
由d(☉T,△ABC)=1知T4N=2.
∵∠T4DC=∠C=45°,
∴T4D=2,∴t=4+2.
综上,t=-4或0≤t≤4-2或t=4+2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考特训(四) 圆
1.[2020·陕西] 如图4-T-1,点A,B,C在☉O上,BC∥OA,连接BO并延长,交☉O于点D,连接AC,DC.若∠A=25°,则∠D的大小为 ( )
A.25° B.30° C.40° D.50°
图4-T-1 图4-T-2
2.[2020·兰州] 如图4-T-2,AB是☉O的直径,若∠BAC=20°,则∠ADC的度数为 ( )
A.40° B.60° C.70° D.80°
3.[2018·烟台] 如图4-T-3,四边形ABCD内接于☉O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为 ( )
A.56° B.62° C.68° D.78°
图4-T-3 图4-T-4
4.[2018·咸宁] 如图4-T-4,已知☉O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为 ( )
A.6 B.8 C.5 D.5
5.[2020·乐山] 在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图4-T-5,将△ABC绕点A按逆时针方向旋转90°后得到△AB'C',则图中阴影部分的面积为 ( )
A. B. C. D.π
图4-T-5 图4-T-6
6.[2019·青岛] 如图4-T-6,线段AB经过☉O的圆心,AC,BD分别与☉O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为 ( )
A.π B.2π C.2π D.4π
7.[2019·荆州] 如图4-T-7,C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在上的点D处,且∶=1∶3(表示的长).若将此扇形OAB围成一个圆锥,则圆锥的底面半径与母线长的比为 ( )
A.1∶3 B.1∶π C.1∶4 D.2∶9
图4-T-7 图4-T-8
8.[2018·宁波] 如图4-T-8,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作☉P.当☉P与正方形ABCD的边相切时,BP的长为 .
9.[2019·赤峰] 如图4-T-9,AB为☉O的直径,C,D是半圆O的三等分点,过点C作AD延长线的垂线CE,垂足为E.
(1)求证:CE是☉O的切线;
(2)若☉O的半径为2,求图中阴影部分的面积.
图4-T-9
10.[2020·宿迁] 如图4-T-10,在△ABC中,D是边BC上一点,以BD为直径的☉O经过点A,且∠CAD=∠ABC.
(1)请判断直线AC是不是☉O的切线,并说明理由;
(2)若CD=2,AC=4,求弦AB的长.
图4-T-10
11.[2018·天津] 如图4-T-11,已知AB是☉O的直径,弦CD与AB相交,∠BAC=38°.
(1)如图①,若D为的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作☉O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
图4-T-11
12.[2018·北京] 对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离”,记作d(M,N).已知点A(-2,6),B(-2,-2),C(6,-2).
(1)求d(点O,△ABC);
(2)记函数y=kx(-1≤x≤1,k≠0)的图象为图形G.若d(G,△ABC)=1,直接写出k的取值范围;
(3)☉T的圆心为T(t,0),半径为1.若d(☉T,△ABC)=1,直接写出t的取值范围.
典题讲评与答案详析
1.C [解析] ∵BC∥OA,
∴∠ACB=∠A=25°,
∴∠B=∠AOB=2∠ACB=50°.
∵BD是☉O的直径,∴∠BCD=90°,
∴∠D=90°-∠B=90°-50°=40°.
故选C.
2.C [解析] ∵AB是☉O的直径,∴∠ACB=90°.
∵∠BAC=20°,∴∠ABC=90°-20°=70°,
∴∠ADC=∠ABC=70°.
故选C.
3.C [解析] ∵点I是△ABC的内心,
∴∠BAC=2∠IAC,∠ACB=2∠ICA.
∵∠AIC=124°,
∴∠B=180°-(∠BAC+∠ACB)=180°-2(∠IAC+∠ICA)=180°-2(180°-∠AIC)=68°.
又四边形ABCD内接于☉O,
∴∠CDE=∠B=68°.
4.B [解析] 如图,延长AO交☉O于点E,连接BE,
则∠AOB+∠BOE=180°.
又∵∠AOB+∠COD=180°,
∴∠BOE=∠COD,
∴BE=CD=6.
∵AE为☉O的直径,∴∠ABE=90°,
∴AB==8.
5.B [解析] ∵∠ABC=90°,∠BAC=30°,BC=1,
∴AC=2BC=2,∴AB==,
∴图中阴影部分的面积=--××1=.
6.B 7.D
8.3或4 [解析] ∵正方形ABCD的边长为8,M是AB的中点,∴BM=AB=4.
如图①,当☉P与CD边相切时,设PC=PM=x.
在Rt△PBM中,
∵PM2=BM2+BP2,∴x2=42+(8-x)2,
∴x=5,∴BP=8-x=8-5=3.
如图②,当☉P与AD边相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形,
∴PM=PK=CD=8.
又∵BM=4,
∴BP==4.
综上所述,BP的长为3或4.
9.解:(1)证明:连接OC.
∵C,D为半圆O的三等分点,
∴==,∴∠DAC=∠BAC.
∵OA=OC,∴∠BAC=∠ACO,
∴∠DAC=∠ACO,∴OC∥AD.
∵CE⊥AD,∴CE⊥OC.
又∵OC是☉O的半径,∴CE是☉O的切线.
(2)连接OD.
∵==,
∴∠AOD=∠COD=∠BOC=×180°=60°.
又∵OC=OD,
∴△COD为等边三角形,
∴∠CDO=60°=∠AOD,
∴CD∥AB,∴S△ACD=S△COD,
∴图中阴影部分的面积=S扇形OCD==.
10.解:(1)直线AC是☉O的切线.
理由如下:如图,连接OA.
∵BD为☉O的直径,
∴∠BAD=90°=∠OAB+∠OAD.
∵OA=OB,∴∠OAB=∠ABC.
又∵∠CAD=∠ABC,
∴∠OAB=∠ABC=∠CAD,
∴∠OAD+∠CAD=∠OAD+∠OAB=90°=∠OAC,
∴AC⊥OA.
又∵OA是☉O的半径,
∴直线AC是☉O的切线.
(2)如图,过点A作AE⊥BD于点E,
∴∠AEC=∠AEB=90°.
由(1)知∠OAC=90°,
∴在Rt△OAC中,OC2=AC2+OA2,
∴(OA+2)2=16+OA2,
∴OA=3,∴OC=5,BC=8.
∵S△OAC=OA·AC=OC·AE,
∴AE==,
∴OE===,
∴BE=OB+OE=,
∴AB===.
11.解:(1)如图①,连接OD.
∵AB是☉O的直径,∴∠ACB=90°,
∴∠ABC=90°-∠BAC=90°-38°=52°.
∵D为的中点,∠AOB=180°,
∴∠AOD=90°,∴∠ABD=∠AOD=45°.
(2)如图②,连接OD.
∵DP切☉O于点D,
∴OD⊥DP,即∠ODP=90°.
∵DP∥AC,∠BAC=38°,∴∠P=∠BAC=38°.
∵∠AOD是△ODP的一个外角,
∴∠AOD=∠P+∠ODP=128°,
∴∠ACD=64°.
∵OC=OA,∠BAC=38°,
∴∠OCA=∠BAC=38°,
∴∠OCD=∠ACD-∠OCA=64°-38°=26°.
12.解:(1)如图所示,点O到△ABC的距离的最小值为2,
∴d(点O,△ABC)=2.
(2)如图,函数y=kx(k≠0)的图象经过原点,
在-1≤x≤1范围内,函数图象为线段.
当函数y=kx(-1≤x≤1,k≠0)的图象经过点(1,-1)时,k=-1,此时d(G,△ABC)=1;
当函数y=kx(-1≤x≤1,k≠0)的图象经过点(-1,-1)时,k=1,此时d(G,△ABC)=1.
∴-1≤k≤1.
又∵k≠0,∴-1≤k≤1且k≠0.
(3)如图,☉T与△ABC的位置关系分三种情况:
①当☉T在△ABC的左侧时,d(☉T,△ABC)=1,此时t=-4.
②当☉T在△ABC的内部时,
当点T与原点重合时,d(☉T,△ABC)=1,
此时t=0;
当点T位于T3位置时,由d(☉T,△ABC)=1知T3M=2.
∵AB=BC=8,∠ABC=90°,
∴∠C=∠T3DM=45°,
则T3D=2,
∴t=4-2.
故此时0≤t≤4-2.
③当☉T在△ABC的右侧时,
由d(☉T,△ABC)=1知T4N=2.
∵∠T4DC=∠C=45°,
∴T4D=2,∴t=4+2.
综上,t=-4或0≤t≤4-2或t=4+2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
