2021-2022学年人教A版必修一 2.2.1 对数与对数运算 课件(24张)
文档属性
| 名称 | 2021-2022学年人教A版必修一 2.2.1 对数与对数运算 课件(24张) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-13 13:51:48 | ||
图片预览








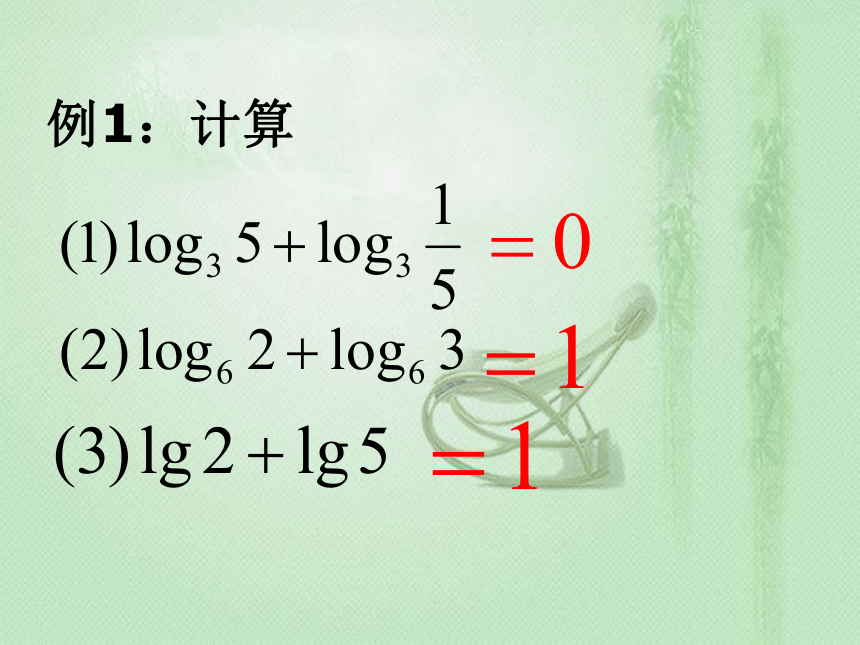
文档简介
(共24张PPT)
第二课时 对数的运算性质
2.2.1 对数与对数运算
1. 对数与指数是怎样互化的?
复习回顾
底数
底数
指数
幂
真数
对数
2.指数的运算性质:
指数与对数可以互化,指数运算有相应的性质,那么对数运算又有哪些性质呢?
问题提出
新授:对数的运算性质
知识探究(一):积与商的对数
log232=log24十log28
思考:求下列对数的值:
(1)log232,log24 ,log28
(2)log33, log39 ,log327
你能发现每组三个对数之间
有什么内在联系?
log327=log33十log39
4X8=32
3X9=27
讨论:通过上面的两个实例,猜想能得到什么样的结论?
猜想:
loga(M·N)=logaM十logaN
其中a>0,且a≠1,M>0,N>0
这个猜想对吗?能否证明?
由指数运算法则得:
证明:设
则
∴
即:
loga(M·N)=logaM十logaN
其中a>0,且a≠1,M>0,N>0
注意括号
真数大于零
例1:计算
问题:
loga(M1M2M3)=?
=logaM1+logaM2+logaM3
(其中a>0且a≠1,M1 , M2 ,M3 >0)
loga(M1M2M3…Mn)
=logaM1+logaM2+logaM3+…+logaMn
(其中a>0且a≠1,M1 , M2 , …Mn>0)
该性质可以推广:
类比思考:
log24= log232-log28
log33=log327-log39
推广到一般情形有什么结论?怎样证明?
4=32÷8
3=27÷9
推广
其中a>0,且a≠1,M>0,N>0
你能证明吗?
由指数运算法则得:
证明:设
则
∴
例2:计算
知识探究(二):幂的对数
思考1: log22与log232有什么关系?
思考2:推广到一般情形有什么结论?
logaMn=nlogaM
其中a>0,且a≠1,M>0
log23与log281有什么关系?
证明:设
则
n可以为任意实数
对数的运算性质
(1) 积的对数等于对数的和.
(2) 商的对数等于对数的差.
(2)
(3)
语言表达:
(3) 幂的对数等于指数倍的对数.
如果 a > 0,a 1,M > 0, N > 0 有:
⑴
对数运算性质需要注意:
(1)注意逆向运算
如
(2)注意限制条件:
底数相同,真数必须是正数;
(3)当心记忆错误:
理论迁移
例3 用logax,logay,logaz表示下列 各式:
(1) (2)
课堂小结
1.对数的运算性质的猜想
2.对数运算性质的推导与证明
3.对数运算性质的简单应用
作业:
P68练习:1, 2,3.
P74习题2.2A组:3,4,5.
第二课时 对数的运算性质
2.2.1 对数与对数运算
1. 对数与指数是怎样互化的?
复习回顾
底数
底数
指数
幂
真数
对数
2.指数的运算性质:
指数与对数可以互化,指数运算有相应的性质,那么对数运算又有哪些性质呢?
问题提出
新授:对数的运算性质
知识探究(一):积与商的对数
log232=log24十log28
思考:求下列对数的值:
(1)log232,log24 ,log28
(2)log33, log39 ,log327
你能发现每组三个对数之间
有什么内在联系?
log327=log33十log39
4X8=32
3X9=27
讨论:通过上面的两个实例,猜想能得到什么样的结论?
猜想:
loga(M·N)=logaM十logaN
其中a>0,且a≠1,M>0,N>0
这个猜想对吗?能否证明?
由指数运算法则得:
证明:设
则
∴
即:
loga(M·N)=logaM十logaN
其中a>0,且a≠1,M>0,N>0
注意括号
真数大于零
例1:计算
问题:
loga(M1M2M3)=?
=logaM1+logaM2+logaM3
(其中a>0且a≠1,M1 , M2 ,M3 >0)
loga(M1M2M3…Mn)
=logaM1+logaM2+logaM3+…+logaMn
(其中a>0且a≠1,M1 , M2 , …Mn>0)
该性质可以推广:
类比思考:
log24= log232-log28
log33=log327-log39
推广到一般情形有什么结论?怎样证明?
4=32÷8
3=27÷9
推广
其中a>0,且a≠1,M>0,N>0
你能证明吗?
由指数运算法则得:
证明:设
则
∴
例2:计算
知识探究(二):幂的对数
思考1: log22与log232有什么关系?
思考2:推广到一般情形有什么结论?
logaMn=nlogaM
其中a>0,且a≠1,M>0
log23与log281有什么关系?
证明:设
则
n可以为任意实数
对数的运算性质
(1) 积的对数等于对数的和.
(2) 商的对数等于对数的差.
(2)
(3)
语言表达:
(3) 幂的对数等于指数倍的对数.
如果 a > 0,a 1,M > 0, N > 0 有:
⑴
对数运算性质需要注意:
(1)注意逆向运算
如
(2)注意限制条件:
底数相同,真数必须是正数;
(3)当心记忆错误:
理论迁移
例3 用logax,logay,logaz表示下列 各式:
(1) (2)
课堂小结
1.对数的运算性质的猜想
2.对数运算性质的推导与证明
3.对数运算性质的简单应用
作业:
P68练习:1, 2,3.
P74习题2.2A组:3,4,5.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
