2021-2022学年人教版七年级数学上册4.3.2角的比较与运算同步练习(word解析版)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册4.3.2角的比较与运算同步练习(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 281.5KB | ||
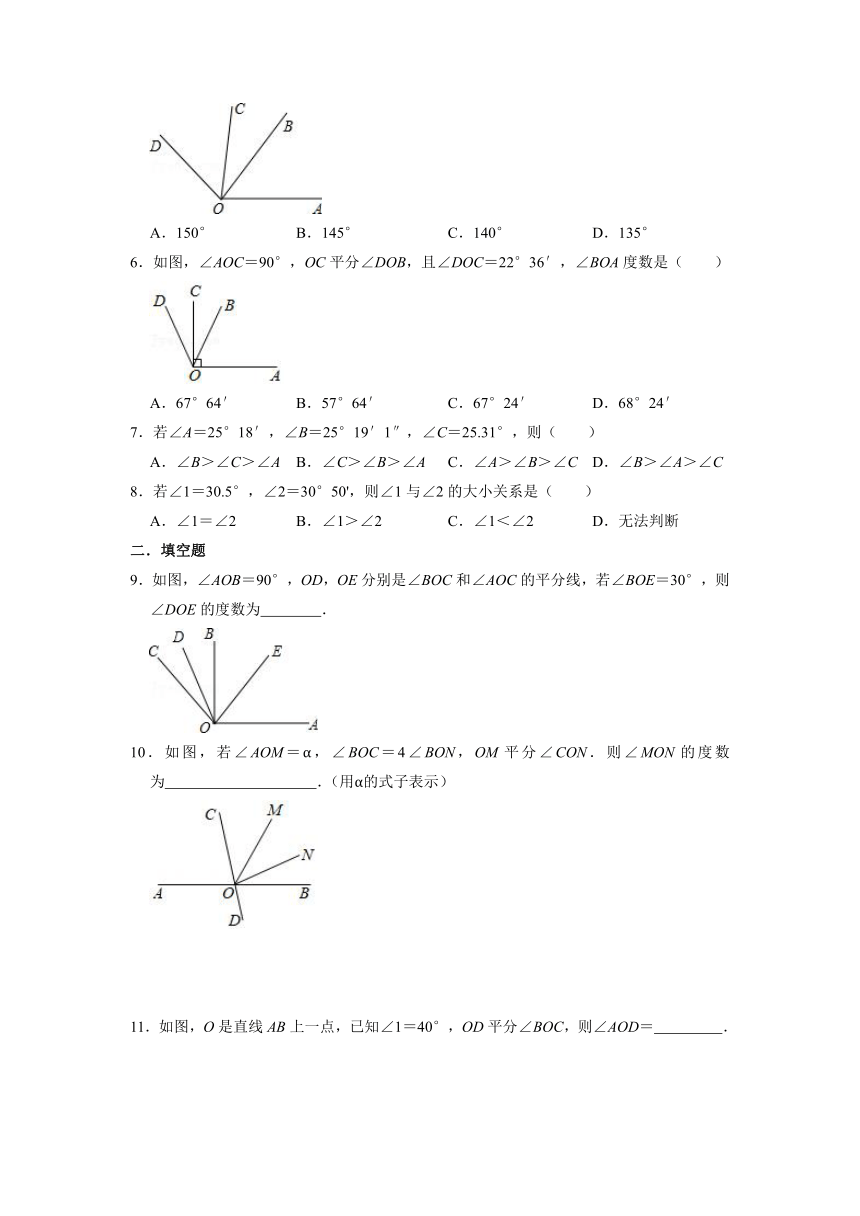
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 15:23:50 | ||
图片预览


文档简介
4.3.2角的比较与运算
一.选择题
1.下列四个说法:
①射线AB和射线BA是同一条射线;
②两点之间,线段最短;
③38°15'和38.15°相等;
④已知三条射线OA,OB,OC,若∠AOC=∠AOB,则射线OC是∠AOB的平分线.
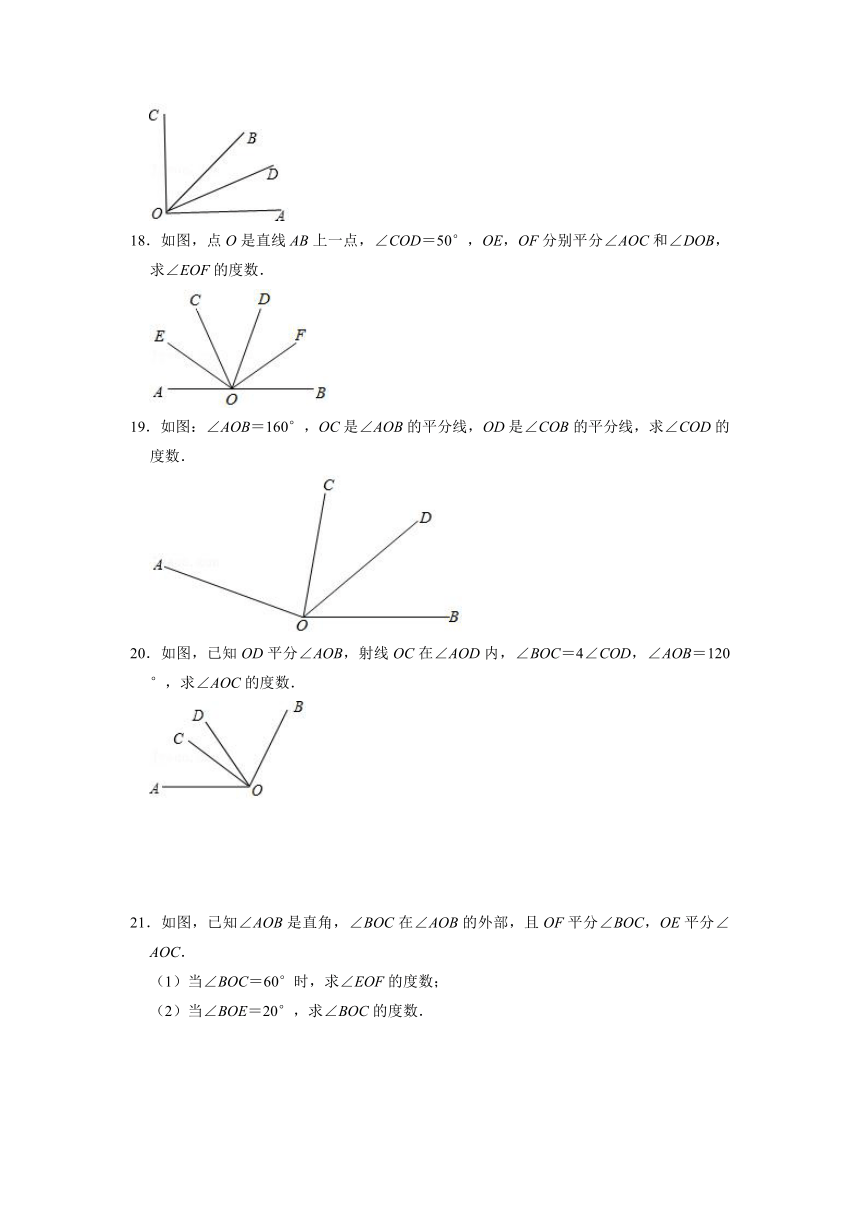
其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
2.如图用一副三角板可以画出15°的角,用它们还可以画出其它一些特殊角,不能利用这副三角板直接画出的角度是( )
A.55° B.75° C.105° D.135°
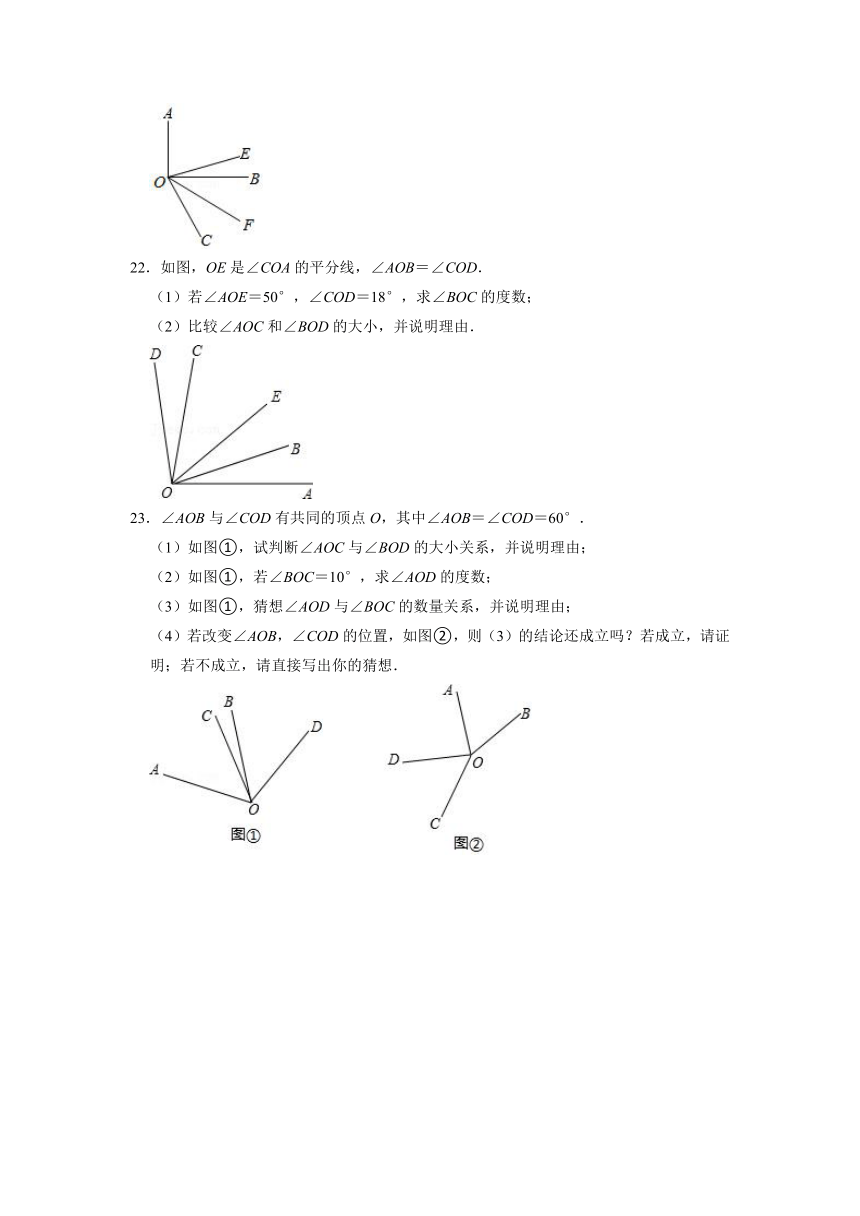
3.如图,OC为∠AOB内的一条射线,下列条件中不能确定OC平分∠AOB的是( )
A.∠AOC=∠BOC B.∠AOC+∠COB=∠AOB
C.∠AOB=2∠BOC D.
4.如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于( )
A.110° B.145° C.35° D.70°
5.如图,已知∠AOC=∠BOD=80°,∠BOC=25°,则∠AOD的度数为( )
A.150° B.145° C.140° D.135°
6.如图,∠AOC=90°,OC平分∠DOB,且∠DOC=22°36′,∠BOA度数是( )
A.67°64′ B.57°64′ C.67°24′ D.68°24′
7.若∠A=25°18′,∠B=25°19′1″,∠C=25.31°,则( )
A.∠B>∠C>∠A B.∠C>∠B>∠A C.∠A>∠B>∠C D.∠B>∠A>∠C
8.若∠1=30.5°,∠2=30°50',则∠1与∠2的大小关系是( )
A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法判断
二.填空题
9.如图,∠AOB=90°,OD,OE分别是∠BOC和∠AOC的平分线,若∠BOE=30°,则∠DOE的度数为 .
10.如图,若∠AOM=α,∠BOC=4∠BON,OM平分∠CON.则∠MON的度数为 .(用α的式子表示)
11.如图,O是直线AB上一点,已知∠1=40°,OD平分∠BOC,则∠AOD= .
12.如图,已知∠AOB=90°,射线OC在∠AOB内部,OD平分∠AOC,OE平分∠BOC,则∠DOE= °.
13.已知∠AOB=50°,OC平分∠AOB,∠BOD=15°,则∠COD= 度.
14.如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF,将∠BEF对折B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′得折痕EN,若∠BEM=62°15′,则∠AEN= .
15.已知∠α=20′,∠β=0.35°,则∠α ∠β.(填“>”,“=”,或“<”)
16.比较大小:52°52′ 52.52°.(填“>”、“<”或“=”)
三.解答题
17.如图,已知∠AOC=90°,∠COD比∠DOA大28°,OB是∠AOC的平分线.求∠BOD的度数.
18.如图,点O是直线AB上一点,∠COD=50°,OE,OF分别平分∠AOC和∠DOB,求∠EOF的度数.
19.如图:∠AOB=160°,OC是∠AOB的平分线,OD是∠COB的平分线,求∠COD的度数.
20.如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=4∠COD,∠AOB=120°,求∠AOC的度数.
21.如图,已知∠AOB是直角,∠BOC在∠AOB的外部,且OF平分∠BOC,OE平分∠AOC.
(1)当∠BOC=60°时,求∠EOF的度数;
(2)当∠BOE=20°,求∠BOC的度数.
22.如图,OE是∠COA的平分线,∠AOB=∠COD.
(1)若∠AOE=50°,∠COD=18°,求∠BOC的度数;
(2)比较∠AOC和∠BOD的大小,并说明理由.
23.∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.
参考答案与试题解析
一.选择题
1.下列四个说法:
①射线AB和射线BA是同一条射线;
②两点之间,线段最短;
③38°15'和38.15°相等;
④已知三条射线OA,OB,OC,若∠AOC=∠AOB,则射线OC是∠AOB的平分线.
其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】根据射线的性质;数轴上两点间的距离的定义;角平分线的定义,线段的性质解答即可.
【解答】解:①射线AB和射线BA表示不是同一条直线,故此选项错误;
②两点之间,线段最短,故此选项正确;
③38°15'=38.25°,故此选项正确;
④已知三条射线OA,OB,OC,若∠AOC=∠AOB,则OC不一定在∠AOB的内部,故此选项错误;
综上所述,正确的是②③,
故选:B.
【点评】本题考查了射线的性质;数轴上两点间的距离的定义;角平分线的定义,线段的性质等知识,解题的关键是了解直线的性质;数轴上两点间的距离的定义等.
2.如图用一副三角板可以画出15°的角,用它们还可以画出其它一些特殊角,不能利用这副三角板直接画出的角度是( )
A.55° B.75° C.105° D.135°
【分析】利用角的和差关系,通过计算得结论.
【解答】解:因为一副三角板有30°、45°、60°、90°的角,
又∵45°﹣30°=15°,45°+30°=75°,
45°+60°=105°,45°+90°=135°.
所以用一副三角板可以画出75°、105°、135°等特殊的角.
故选:A.
【点评】本题考查了角的和差及角的计算.能够熟练计算角的和差度数,是解决本题的关键.
3.如图,OC为∠AOB内的一条射线,下列条件中不能确定OC平分∠AOB的是( )
A.∠AOC=∠BOC B.∠AOC+∠COB=∠AOB
C.∠AOB=2∠BOC D.
【分析】根据角平分线的定义可直接判定求解.
【解答】解:∵OC为∠AOB内的一条射线,
∴当∠AOC=∠BOC=∠AOB,或∠AOB=2∠BOC=2∠AOC时OC平分∠AOB,
∴A,C,D不符合题意,B选项符合题意,
故选:B.
【点评】本题主要考查角平分线的定义,掌握角平分线的定义是解题的关键.
4.如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于( )
A.110° B.145° C.35° D.70°
【分析】首先根据角平分线定义可得∠BOD=2∠BOC=70°,再根据邻补角的性质可得∠AOD的度数.
【解答】解:∵射线OC平分∠DOB.
∴∠BOD=2∠BOC,
∵∠COB=35°,
∴∠DOB=70°,
∴∠AOD=180°﹣70°=110°,
故选:A.
【点评】此题主要考查了角平分线定义和邻补角的定义,关键是掌握角平分线把角分成相等的两部分.
5.如图,已知∠AOC=∠BOD=80°,∠BOC=25°,则∠AOD的度数为( )
A.150° B.145° C.140° D.135°
【分析】先求∠AOC与∠BOC的度数差即可得出∠AOB的度数,再求∠AOB与∠DOB的和即可.
【解答】解:∵∠AOC=∠BOD=80°,∠BOC=25°,
∴∠AOB=∠AOC﹣∠BOC=80°﹣25°=55°,
∴∠AOD=∠BOD+∠AOB=80°+55°=135°,
故选:D.
【点评】本题考查了角的运算,较为简单,解题关键是不要忘了减去两个角的重合部分.
6.如图,∠AOC=90°,OC平分∠DOB,且∠DOC=22°36′,∠BOA度数是( )
A.67°64′ B.57°64′ C.67°24′ D.68°24′
【分析】先利用角平分线的定义求出∠DOC的度数,再利用角的和差及互余关系求出∠BOA度数.
【解答】解:∵OC平分∠DOB,
∴∠DOC=∠BOC=22°36′.
∵∠AOC=∠AOB+∠BOC=90°,
∴∠AOB=∠AOC﹣∠BOC
=90°﹣22°36′
=67°24′.
故选:C.
【点评】本题考查了角平分线的定义、两角互余等知识点,掌握角的和差关系是解决本题的关键.
7.若∠A=25°18′,∠B=25°19′1″,∠C=25.31°,则( )
A.∠B>∠C>∠A B.∠C>∠B>∠A C.∠A>∠B>∠C D.∠B>∠A>∠C
【分析】把25.31°化为25°18′36″,再比较大小即可.
【解答】解:因为∠C=25.31°=25°18′36″,25°19′1″>25°18′36″>25°18′,
所以∠B>∠C>∠A.
故选:A.
【点评】本题主要考查了角的大小比较,熟练掌握角的单位换算是解答本题的关键.
8.若∠1=30.5°,∠2=30°50',则∠1与∠2的大小关系是( )
A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法判断
【分析】将30.5°化成30°30′后,再进行比较即可.
【解答】解:因为0.5°=0.5×60′=30′,
所以∠1=30.5°=30°30′,
而∠2=30°50',
所以∠1<∠2,
故选:C.
【点评】本题考查角的大小比较,掌握度、分、秒的换算是解决问题的前提,化成“同名”是正确比较的关键.
二.填空题
9.如图,∠AOB=90°,OD,OE分别是∠BOC和∠AOC的平分线,若∠BOE=30°,则∠DOE的度数为 45° .
【分析】先求出∠AOE=60°,再求出∠COE=∠AOE=60°,然后由OD平分∠BOC,得出∠BOD=∠BOC=15°,即可求出∠DOE=∠BOD+∠BOE=45°.
【解答】解:∵∠AOB=90°,∠BOE=30°,
∴∠AOE=90°﹣30°=60°,
∵OE平分∠AOC,
∴∠COE=∠AOE=60°,
∴∠BOC=60°﹣30°=30°,
∵OD平分∠BOC,
∴∠BOD=∠BOC=15°,
∴∠DOE=∠BOD+∠BOE=45°;
故答案为:45°.
【点评】本题考查了角平分线的定义;弄清各个角之间的数量关系是解决问题的关键.
10.如图,若∠AOM=α,∠BOC=4∠BON,OM平分∠CON.则∠MON的度数为 .(用α的式子表示)
【分析】设∠BON=x,∠BOC=4x,根据角平分线的定义得到∠MON=∠CON=x,∠BOM=∠MON+∠NOB=x+x=180°﹣α,解方程求出x,进一步即可求得即∠MON的度数.
【解答】解:设∠BON=x,则∠BOC=4x,
∵∠BOC=4∠BON,
∴∠CON=∠COB﹣∠BON=4x﹣x=3x,
∵OM平分∠CON,
∴∠MON=∠CON=x,
∵∠AOM=α,
∴∠BOM=∠MON+∠BON=x+x=180°﹣α,
∴x=,
∴∠MON=x=×=,
即∠MON的度数为.
故答案为:.
【点评】本题考查的是邻补角的概念和性质,角平分线的定义,掌握邻补角、角平分线的定义是解题的关键.
11.如图,O是直线AB上一点,已知∠1=40°,OD平分∠BOC,则∠AOD= 110° .
【分析】根据邻补角求出∠COB,根据角平分线定义求出∠2=∠COB,代入求出即可.
【解答】解:∵∠1=40°,
∴∠COB=180°﹣∠1=140°,
∵OD平分∠COB,
∴∠2=∠COB=×140°=70°,
∴∠AOD=180°﹣70°=110°.
故答案为:110°.
【点评】本题考查了邻补角和角平分线定义的应用,解此题的关键是能求出∠COB的度数和得出∠2=∠COB,注意:从角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线就叫角的平分线.
12.如图,已知∠AOB=90°,射线OC在∠AOB内部,OD平分∠AOC,OE平分∠BOC,则∠DOE= 45 °.
【分析】根据角平分线的定义得到∠DOC=∠BOC,∠COE=∠COA,结合图形计算即可.
【解答】解:∵OD平分∠AOC,
∴∠DOC=∠AOC,
∵OE平分∠BOC,
∴∠COE=∠BOC,
∴∠DOE=∠DOC+∠COE= (∠BOC+∠COA)=∠AOB=45°.
故答案为:45.
【点评】本题考查的是角平分线的定义,角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
13.已知∠AOB=50°,OC平分∠AOB,∠BOD=15°,则∠COD= 10或40 度.
【分析】根据题意画出图形,分两种情况:①OD在∠AOB的内部;②OD在∠AOB的外部.先求出∠BOC,再求出∠COD.
【解答】解:根据题意画出图形如图所示:
∵∠AOB=50°,OC平分∠AOB,
∴∠BOC=∠AOB=×50°=25°.
①OD在∠AOB的内部,
∵∠BOD=15°,
∴∠COD=∠BOC﹣∠BOD=25°﹣15°=10°.
②OD在∠AOB的外部,图中的OD′,
∵∠BOD′=15°,
∴∠COD′=∠BOC+∠BOD′=25°+15°=40°.
综上所述,∠COD是10°或40°.
故答案为:10度或40.
【点评】本题考查了角的计算和角平分线的定义.弄清各个角之间的数量关系是解决问题的关键.
14.如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF,将∠BEF对折B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′得折痕EN,若∠BEM=62°15′,则∠AEN= 27°45′ .
【分析】根据折叠的性质即可求解.
【解答】解:根据折叠可知:
EM平分∠BEB′,
∴∠B′EM=∠BEM=62°15′,
∴∠AEA′=180°﹣2×62°15′=55°30′,
EN平分∠AEA′,
∴∠AEN=∠A′EN=AEA′=55°15′=27°45′,
故答案为:27°45′.
【点评】本题考查了角的计算、度分秒的换算,解决本题的关键是准确进行度分秒的换算.
15.已知∠α=20′,∠β=0.35°,则∠α < ∠β.(填“>”,“=”,或“<”)
【分析】根据度分秒之间的换算关系,先把∠β的度数转换成分的形式,再根据角的大小比较的法则进行比较,即可得出答案.
【解答】解:∵∠β=0.35°=(0.35×60)′=21′,
∴∠α<∠β,
故答案为:<.
【点评】此题考查了角的大小比较,掌握度分秒之间的换算法则是解题的关键.
16.比较大小:52°52′ > 52.52°.(填“>”、“<”或“=”)
【分析】将角的度数换算成度分秒的形式,再进行比较即可得出结论、
【解答】解:∵0.52×60=31.2,0.2×60=12,
∴52.52°=52°31′12″,
52°52′>52°31′12″,
故答案为:>.
【点评】本题考查的度分秒的换算以及角的大小比较,解题的关键是将角的度数换算成度分秒的形式,再进行比较.
三.解答题
17.如图①,已知点C、D是线段AB上两点,D是AC的中点,若CB=4cm,DB=7cm.
(1)求线段AB的长;
(2)如图②,若M,N分别为AD,CB的中点,求线段MN的长;
(3)类比以上探究,如图③,解决以下问题:射线OA,OB分别为∠MOP和∠NOP的平分线,∠MON=α,∠NOP=β(β<α).求∠AOB的大小.
【分析】(1)根据线段的中点定义即可求出AB的长;
(2)结合(1)根据线段的中点定义即可求出MN的长;
(3)根据角平分线的定义和角的和差即可求出结果.
【解答】解:(1)∵CB=4cm,DB=7cm.
∴DC=DB﹣CB=3cm.
∵D是AC的中点,
∴AC=2DC=6cm.
∴AB=AC+CB=10cm;
(2)由(1)知:AD=DC=3cm,
∵M,N分别为AD,CB的中点,
∴MD=AD=1.5cm,CN=BC=2cm,
∴MN=MD+DC+CN=1.5+3+2=6.5(cm);
(3)∵∠MON=α,∠NOP=β,
∴∠MOP=∠MON+∠NOP=α+β,
∵OA,OB分别为∠MOP和∠NOP的平分线,
∴∠AOM=∠AOP=MOP=(α+β),
∠BOP=NOP=,
∴∠AOB=∠AOP﹣∠BOP=(α+β)﹣=.
【点评】本题考查了角平分线定义,两点间的距离,利用线段的和差和角的和差进行计算是解题关键
18.如图,已知∠AOC=90°,∠COD比∠DOA大28°,OB是∠AOC的平分线.求∠BOD的度数.
【分析】先由∠COD﹣∠DOA=28°,∠COD+∠DOA=90°,解方程求出∠COD与∠DOA的度数,再由OB是∠AOC的平分线,得出∠AOB=∠AOC=45°,则∠BOD=∠AOB﹣∠DOA,求出结果.
【解答】解:∵∠COD比∠DOA大28°,
∴∠COD=∠DOA+28°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+28°+∠DOA=90°,
2∠DOA=62°,所以∠DOA=31°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC=∠AOC=45°,
∴∠BOD=∠AOB﹣∠DOA=45°﹣31°=14°.
故答案为14°.
【点评】本题主要考查了角平分线的定义及利用方程思想求角的大小.
19.如图,点O是直线AB上一点,∠COD=50°,OE,OF分别平分∠AOC和∠DOB,求∠EOF的度数.
【分析】首先利用平角的定义求得∠AOC+∠BOD的度数,然后利用角平分线的定义得到∠EOC+∠DOF的度数,然后求得∠EOF的度数即可.
【解答】解:∵∠COD=50°,
∴∠AOC+∠BOD=180°﹣∠COD=180°﹣50°=130°,
∵OE,OF分别平分∠AOC和∠DOB,
∴∠AOE=∠COE,∠DOF=∠BOF,
∴∠EOC+∠DOF=(∠AOC+∠BOD)=65°,
∴∠EOF=∠EOC+∠DOF+∠COD=65°+50°=115°.
【点评】本题考查了角平分线的定义的知识,属于基础题,比较简单,理清各个角之间的关系是解决本题的重点.
20.如图:∠AOB=160°,OC是∠AOB的平分线,OD是∠COB的平分线,求∠COD的度数.
【分析】首先根据角平分线的定义求得∠COB的度数,然后根据角平分线的定义求得∠COD的度数.
【解答】解:∵OC是∠AOB的平分线,∠AOB=160°,
∴∠COB=∠AOB=80°,
又∵OD是∠COB的平分线,
∴∠COD=∠COB=40°.
【点评】本题考查了角平分线的定义,正确求得∠COB的度数是解题的关键.
21.如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=4∠COD,∠AOB=120°,求∠AOC的度数.
【分析】根据OD平分∠AOB可得出∠AOD=∠BOD,再由∠BOC=4∠COD可设∠COD=x,则∠BOD=3x,AOC=2x,再由∠AOB=120°可得出x的值,进而得出结论.
【解答】解:∵OD平分∠AOB,
∴∠AOD=∠BOD.
∵∠BOC=4∠COD,
∴设∠COD=x,则∠BOD=3x,AOC=2x,
∵∠AOB=120°,
∴2x+x+3x=120°,解得x=20°,
∴∠AOC=2x=40°.
【点评】本题考查的是角的计算,熟知角平分线的定义是解答此题的关键.
22.如图,已知∠AOB是直角,∠BOC在∠AOB的外部,且OF平分∠BOC,OE平分∠AOC.
(1)当∠BOC=60°时,求∠EOF的度数;
(2)当∠BOE=20°,求∠BOC的度数.
【分析】(1)利用角平分线的定义和角的和差的意义即可解答;
(2)由∠BOE=20°,可得∠AOE=70°,由角平分线的意义可得∠EOC=∠AOE=70°,则∠BOC=∠EOC﹣∠BOE.
【解答】解:(1)∠AOB是直角,∠BOC=60°,
∴∠AOC=∠AOB+∠BOC=150°.
∵OE平分∠AOC,
∴∠EOC=∠AOC=75°,
∵OF平分∠BOC,∠BOC=60°,
∴∠FOC=∠BOC=30°.
∴∠EOF=∠EOC﹣∠FOC=45°;
(2)∵∠BOE=20°,∠AOB是直角,
∴∠AOE=∠AOB﹣∠BOE=70°,
∵OE平分∠AOC,
∴∠AOE=∠EOC=70°,
∴∠BOC=∠EOC﹣∠BOE=70°﹣20°=50°.
【点评】本题主要考查了角的计算,角平分线的定义.充分利用图形中角的和差的意义与角平分线的定义是解题的关键.
23.如图,OE是∠COA的平分线,∠AOB=∠COD.
(1)若∠AOE=50°,∠COD=18°,求∠BOC的度数;
(2)比较∠AOC和∠BOD的大小,并说明理由.
【分析】(1)依据角平分线的定义,即可得到∠AOC的度数,再根据角的和差关系,即可得出∠BOC的度数;
(2)依据等式的性质,即可得到∠AOC=∠BOD.
【解答】解:(1)∵OE是∠COA的平分线,∠AOE=50°,
∴∠AOC=2∠AOE=100°,
又∵∠AOB=∠COD=18°,
∴∠BOC=∠AOC﹣∠AOB=100°﹣18°=82°;
(2)∠AOC=∠BOD.
理由:∵∠AOB=∠COD,
∴∠AOB+∠BOC=∠COD+∠BOC,
∴∠AOC=∠BOD.
【点评】本题主要考查了角的大小比较以及角平分线的定义的运用,从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
24.∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.
【分析】(1)利用角的和差定义证明即可;
(2)求出∠AOC即可解决问题;
(3)结论:∠AOD+∠COB=120°.利用角的和差定义证明即可;
(4)不成立.猜想:∠AOD+∠BOC=240°,根据周角的性质证明即可;
【解答】解:(1)结论:∠AOC=∠BOD.
理由:∵∠AOB=∠COD=60°,
∴∠AOC+∠BOC=∠BOD+∠BOC,
∴∠AOC=∠BOD.
(2)∵∠BCO=10°,∠AOB=60°,
∴∠AOC=50°,
∴∠AOD=∠AOC+∠COD=50°+60°=110°.
(3)猜想:∠AOD+∠COB=120°.
理由:∵∠AOB=∠COD=60°.
∴∠AOD=∠AOB+∠COD﹣∠COB=120°﹣∠COB,
∴∠AOD+∠COB=120°.
(4)不成立.猜想:∠AOD+∠BOC=240°,
理由:∵∠AOB=∠COD=60°.
∴∠AOD+∠BOC=360°﹣60°﹣60°=240°.
【点评】本题考查角的计算,角的和差定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考基础题.
一.选择题
1.下列四个说法:
①射线AB和射线BA是同一条射线;
②两点之间,线段最短;
③38°15'和38.15°相等;
④已知三条射线OA,OB,OC,若∠AOC=∠AOB,则射线OC是∠AOB的平分线.
其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
2.如图用一副三角板可以画出15°的角,用它们还可以画出其它一些特殊角,不能利用这副三角板直接画出的角度是( )
A.55° B.75° C.105° D.135°
3.如图,OC为∠AOB内的一条射线,下列条件中不能确定OC平分∠AOB的是( )
A.∠AOC=∠BOC B.∠AOC+∠COB=∠AOB
C.∠AOB=2∠BOC D.
4.如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于( )
A.110° B.145° C.35° D.70°
5.如图,已知∠AOC=∠BOD=80°,∠BOC=25°,则∠AOD的度数为( )
A.150° B.145° C.140° D.135°
6.如图,∠AOC=90°,OC平分∠DOB,且∠DOC=22°36′,∠BOA度数是( )
A.67°64′ B.57°64′ C.67°24′ D.68°24′
7.若∠A=25°18′,∠B=25°19′1″,∠C=25.31°,则( )
A.∠B>∠C>∠A B.∠C>∠B>∠A C.∠A>∠B>∠C D.∠B>∠A>∠C
8.若∠1=30.5°,∠2=30°50',则∠1与∠2的大小关系是( )
A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法判断
二.填空题
9.如图,∠AOB=90°,OD,OE分别是∠BOC和∠AOC的平分线,若∠BOE=30°,则∠DOE的度数为 .
10.如图,若∠AOM=α,∠BOC=4∠BON,OM平分∠CON.则∠MON的度数为 .(用α的式子表示)
11.如图,O是直线AB上一点,已知∠1=40°,OD平分∠BOC,则∠AOD= .
12.如图,已知∠AOB=90°,射线OC在∠AOB内部,OD平分∠AOC,OE平分∠BOC,则∠DOE= °.
13.已知∠AOB=50°,OC平分∠AOB,∠BOD=15°,则∠COD= 度.
14.如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF,将∠BEF对折B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′得折痕EN,若∠BEM=62°15′,则∠AEN= .
15.已知∠α=20′,∠β=0.35°,则∠α ∠β.(填“>”,“=”,或“<”)
16.比较大小:52°52′ 52.52°.(填“>”、“<”或“=”)
三.解答题
17.如图,已知∠AOC=90°,∠COD比∠DOA大28°,OB是∠AOC的平分线.求∠BOD的度数.
18.如图,点O是直线AB上一点,∠COD=50°,OE,OF分别平分∠AOC和∠DOB,求∠EOF的度数.
19.如图:∠AOB=160°,OC是∠AOB的平分线,OD是∠COB的平分线,求∠COD的度数.
20.如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=4∠COD,∠AOB=120°,求∠AOC的度数.
21.如图,已知∠AOB是直角,∠BOC在∠AOB的外部,且OF平分∠BOC,OE平分∠AOC.
(1)当∠BOC=60°时,求∠EOF的度数;
(2)当∠BOE=20°,求∠BOC的度数.
22.如图,OE是∠COA的平分线,∠AOB=∠COD.
(1)若∠AOE=50°,∠COD=18°,求∠BOC的度数;
(2)比较∠AOC和∠BOD的大小,并说明理由.
23.∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.
参考答案与试题解析
一.选择题
1.下列四个说法:
①射线AB和射线BA是同一条射线;
②两点之间,线段最短;
③38°15'和38.15°相等;
④已知三条射线OA,OB,OC,若∠AOC=∠AOB,则射线OC是∠AOB的平分线.
其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】根据射线的性质;数轴上两点间的距离的定义;角平分线的定义,线段的性质解答即可.
【解答】解:①射线AB和射线BA表示不是同一条直线,故此选项错误;
②两点之间,线段最短,故此选项正确;
③38°15'=38.25°,故此选项正确;
④已知三条射线OA,OB,OC,若∠AOC=∠AOB,则OC不一定在∠AOB的内部,故此选项错误;
综上所述,正确的是②③,
故选:B.
【点评】本题考查了射线的性质;数轴上两点间的距离的定义;角平分线的定义,线段的性质等知识,解题的关键是了解直线的性质;数轴上两点间的距离的定义等.
2.如图用一副三角板可以画出15°的角,用它们还可以画出其它一些特殊角,不能利用这副三角板直接画出的角度是( )
A.55° B.75° C.105° D.135°
【分析】利用角的和差关系,通过计算得结论.
【解答】解:因为一副三角板有30°、45°、60°、90°的角,
又∵45°﹣30°=15°,45°+30°=75°,
45°+60°=105°,45°+90°=135°.
所以用一副三角板可以画出75°、105°、135°等特殊的角.
故选:A.
【点评】本题考查了角的和差及角的计算.能够熟练计算角的和差度数,是解决本题的关键.
3.如图,OC为∠AOB内的一条射线,下列条件中不能确定OC平分∠AOB的是( )
A.∠AOC=∠BOC B.∠AOC+∠COB=∠AOB
C.∠AOB=2∠BOC D.
【分析】根据角平分线的定义可直接判定求解.
【解答】解:∵OC为∠AOB内的一条射线,
∴当∠AOC=∠BOC=∠AOB,或∠AOB=2∠BOC=2∠AOC时OC平分∠AOB,
∴A,C,D不符合题意,B选项符合题意,
故选:B.
【点评】本题主要考查角平分线的定义,掌握角平分线的定义是解题的关键.
4.如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于( )
A.110° B.145° C.35° D.70°
【分析】首先根据角平分线定义可得∠BOD=2∠BOC=70°,再根据邻补角的性质可得∠AOD的度数.
【解答】解:∵射线OC平分∠DOB.
∴∠BOD=2∠BOC,
∵∠COB=35°,
∴∠DOB=70°,
∴∠AOD=180°﹣70°=110°,
故选:A.
【点评】此题主要考查了角平分线定义和邻补角的定义,关键是掌握角平分线把角分成相等的两部分.
5.如图,已知∠AOC=∠BOD=80°,∠BOC=25°,则∠AOD的度数为( )
A.150° B.145° C.140° D.135°
【分析】先求∠AOC与∠BOC的度数差即可得出∠AOB的度数,再求∠AOB与∠DOB的和即可.
【解答】解:∵∠AOC=∠BOD=80°,∠BOC=25°,
∴∠AOB=∠AOC﹣∠BOC=80°﹣25°=55°,
∴∠AOD=∠BOD+∠AOB=80°+55°=135°,
故选:D.
【点评】本题考查了角的运算,较为简单,解题关键是不要忘了减去两个角的重合部分.
6.如图,∠AOC=90°,OC平分∠DOB,且∠DOC=22°36′,∠BOA度数是( )
A.67°64′ B.57°64′ C.67°24′ D.68°24′
【分析】先利用角平分线的定义求出∠DOC的度数,再利用角的和差及互余关系求出∠BOA度数.
【解答】解:∵OC平分∠DOB,
∴∠DOC=∠BOC=22°36′.
∵∠AOC=∠AOB+∠BOC=90°,
∴∠AOB=∠AOC﹣∠BOC
=90°﹣22°36′
=67°24′.
故选:C.
【点评】本题考查了角平分线的定义、两角互余等知识点,掌握角的和差关系是解决本题的关键.
7.若∠A=25°18′,∠B=25°19′1″,∠C=25.31°,则( )
A.∠B>∠C>∠A B.∠C>∠B>∠A C.∠A>∠B>∠C D.∠B>∠A>∠C
【分析】把25.31°化为25°18′36″,再比较大小即可.
【解答】解:因为∠C=25.31°=25°18′36″,25°19′1″>25°18′36″>25°18′,
所以∠B>∠C>∠A.
故选:A.
【点评】本题主要考查了角的大小比较,熟练掌握角的单位换算是解答本题的关键.
8.若∠1=30.5°,∠2=30°50',则∠1与∠2的大小关系是( )
A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法判断
【分析】将30.5°化成30°30′后,再进行比较即可.
【解答】解:因为0.5°=0.5×60′=30′,
所以∠1=30.5°=30°30′,
而∠2=30°50',
所以∠1<∠2,
故选:C.
【点评】本题考查角的大小比较,掌握度、分、秒的换算是解决问题的前提,化成“同名”是正确比较的关键.
二.填空题
9.如图,∠AOB=90°,OD,OE分别是∠BOC和∠AOC的平分线,若∠BOE=30°,则∠DOE的度数为 45° .
【分析】先求出∠AOE=60°,再求出∠COE=∠AOE=60°,然后由OD平分∠BOC,得出∠BOD=∠BOC=15°,即可求出∠DOE=∠BOD+∠BOE=45°.
【解答】解:∵∠AOB=90°,∠BOE=30°,
∴∠AOE=90°﹣30°=60°,
∵OE平分∠AOC,
∴∠COE=∠AOE=60°,
∴∠BOC=60°﹣30°=30°,
∵OD平分∠BOC,
∴∠BOD=∠BOC=15°,
∴∠DOE=∠BOD+∠BOE=45°;
故答案为:45°.
【点评】本题考查了角平分线的定义;弄清各个角之间的数量关系是解决问题的关键.
10.如图,若∠AOM=α,∠BOC=4∠BON,OM平分∠CON.则∠MON的度数为 .(用α的式子表示)
【分析】设∠BON=x,∠BOC=4x,根据角平分线的定义得到∠MON=∠CON=x,∠BOM=∠MON+∠NOB=x+x=180°﹣α,解方程求出x,进一步即可求得即∠MON的度数.
【解答】解:设∠BON=x,则∠BOC=4x,
∵∠BOC=4∠BON,
∴∠CON=∠COB﹣∠BON=4x﹣x=3x,
∵OM平分∠CON,
∴∠MON=∠CON=x,
∵∠AOM=α,
∴∠BOM=∠MON+∠BON=x+x=180°﹣α,
∴x=,
∴∠MON=x=×=,
即∠MON的度数为.
故答案为:.
【点评】本题考查的是邻补角的概念和性质,角平分线的定义,掌握邻补角、角平分线的定义是解题的关键.
11.如图,O是直线AB上一点,已知∠1=40°,OD平分∠BOC,则∠AOD= 110° .
【分析】根据邻补角求出∠COB,根据角平分线定义求出∠2=∠COB,代入求出即可.
【解答】解:∵∠1=40°,
∴∠COB=180°﹣∠1=140°,
∵OD平分∠COB,
∴∠2=∠COB=×140°=70°,
∴∠AOD=180°﹣70°=110°.
故答案为:110°.
【点评】本题考查了邻补角和角平分线定义的应用,解此题的关键是能求出∠COB的度数和得出∠2=∠COB,注意:从角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线就叫角的平分线.
12.如图,已知∠AOB=90°,射线OC在∠AOB内部,OD平分∠AOC,OE平分∠BOC,则∠DOE= 45 °.
【分析】根据角平分线的定义得到∠DOC=∠BOC,∠COE=∠COA,结合图形计算即可.
【解答】解:∵OD平分∠AOC,
∴∠DOC=∠AOC,
∵OE平分∠BOC,
∴∠COE=∠BOC,
∴∠DOE=∠DOC+∠COE= (∠BOC+∠COA)=∠AOB=45°.
故答案为:45.
【点评】本题考查的是角平分线的定义,角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
13.已知∠AOB=50°,OC平分∠AOB,∠BOD=15°,则∠COD= 10或40 度.
【分析】根据题意画出图形,分两种情况:①OD在∠AOB的内部;②OD在∠AOB的外部.先求出∠BOC,再求出∠COD.
【解答】解:根据题意画出图形如图所示:
∵∠AOB=50°,OC平分∠AOB,
∴∠BOC=∠AOB=×50°=25°.
①OD在∠AOB的内部,
∵∠BOD=15°,
∴∠COD=∠BOC﹣∠BOD=25°﹣15°=10°.
②OD在∠AOB的外部,图中的OD′,
∵∠BOD′=15°,
∴∠COD′=∠BOC+∠BOD′=25°+15°=40°.
综上所述,∠COD是10°或40°.
故答案为:10度或40.
【点评】本题考查了角的计算和角平分线的定义.弄清各个角之间的数量关系是解决问题的关键.
14.如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF,将∠BEF对折B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′得折痕EN,若∠BEM=62°15′,则∠AEN= 27°45′ .
【分析】根据折叠的性质即可求解.
【解答】解:根据折叠可知:
EM平分∠BEB′,
∴∠B′EM=∠BEM=62°15′,
∴∠AEA′=180°﹣2×62°15′=55°30′,
EN平分∠AEA′,
∴∠AEN=∠A′EN=AEA′=55°15′=27°45′,
故答案为:27°45′.
【点评】本题考查了角的计算、度分秒的换算,解决本题的关键是准确进行度分秒的换算.
15.已知∠α=20′,∠β=0.35°,则∠α < ∠β.(填“>”,“=”,或“<”)
【分析】根据度分秒之间的换算关系,先把∠β的度数转换成分的形式,再根据角的大小比较的法则进行比较,即可得出答案.
【解答】解:∵∠β=0.35°=(0.35×60)′=21′,
∴∠α<∠β,
故答案为:<.
【点评】此题考查了角的大小比较,掌握度分秒之间的换算法则是解题的关键.
16.比较大小:52°52′ > 52.52°.(填“>”、“<”或“=”)
【分析】将角的度数换算成度分秒的形式,再进行比较即可得出结论、
【解答】解:∵0.52×60=31.2,0.2×60=12,
∴52.52°=52°31′12″,
52°52′>52°31′12″,
故答案为:>.
【点评】本题考查的度分秒的换算以及角的大小比较,解题的关键是将角的度数换算成度分秒的形式,再进行比较.
三.解答题
17.如图①,已知点C、D是线段AB上两点,D是AC的中点,若CB=4cm,DB=7cm.
(1)求线段AB的长;
(2)如图②,若M,N分别为AD,CB的中点,求线段MN的长;
(3)类比以上探究,如图③,解决以下问题:射线OA,OB分别为∠MOP和∠NOP的平分线,∠MON=α,∠NOP=β(β<α).求∠AOB的大小.
【分析】(1)根据线段的中点定义即可求出AB的长;
(2)结合(1)根据线段的中点定义即可求出MN的长;
(3)根据角平分线的定义和角的和差即可求出结果.
【解答】解:(1)∵CB=4cm,DB=7cm.
∴DC=DB﹣CB=3cm.
∵D是AC的中点,
∴AC=2DC=6cm.
∴AB=AC+CB=10cm;
(2)由(1)知:AD=DC=3cm,
∵M,N分别为AD,CB的中点,
∴MD=AD=1.5cm,CN=BC=2cm,
∴MN=MD+DC+CN=1.5+3+2=6.5(cm);
(3)∵∠MON=α,∠NOP=β,
∴∠MOP=∠MON+∠NOP=α+β,
∵OA,OB分别为∠MOP和∠NOP的平分线,
∴∠AOM=∠AOP=MOP=(α+β),
∠BOP=NOP=,
∴∠AOB=∠AOP﹣∠BOP=(α+β)﹣=.
【点评】本题考查了角平分线定义,两点间的距离,利用线段的和差和角的和差进行计算是解题关键
18.如图,已知∠AOC=90°,∠COD比∠DOA大28°,OB是∠AOC的平分线.求∠BOD的度数.
【分析】先由∠COD﹣∠DOA=28°,∠COD+∠DOA=90°,解方程求出∠COD与∠DOA的度数,再由OB是∠AOC的平分线,得出∠AOB=∠AOC=45°,则∠BOD=∠AOB﹣∠DOA,求出结果.
【解答】解:∵∠COD比∠DOA大28°,
∴∠COD=∠DOA+28°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+28°+∠DOA=90°,
2∠DOA=62°,所以∠DOA=31°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC=∠AOC=45°,
∴∠BOD=∠AOB﹣∠DOA=45°﹣31°=14°.
故答案为14°.
【点评】本题主要考查了角平分线的定义及利用方程思想求角的大小.
19.如图,点O是直线AB上一点,∠COD=50°,OE,OF分别平分∠AOC和∠DOB,求∠EOF的度数.
【分析】首先利用平角的定义求得∠AOC+∠BOD的度数,然后利用角平分线的定义得到∠EOC+∠DOF的度数,然后求得∠EOF的度数即可.
【解答】解:∵∠COD=50°,
∴∠AOC+∠BOD=180°﹣∠COD=180°﹣50°=130°,
∵OE,OF分别平分∠AOC和∠DOB,
∴∠AOE=∠COE,∠DOF=∠BOF,
∴∠EOC+∠DOF=(∠AOC+∠BOD)=65°,
∴∠EOF=∠EOC+∠DOF+∠COD=65°+50°=115°.
【点评】本题考查了角平分线的定义的知识,属于基础题,比较简单,理清各个角之间的关系是解决本题的重点.
20.如图:∠AOB=160°,OC是∠AOB的平分线,OD是∠COB的平分线,求∠COD的度数.
【分析】首先根据角平分线的定义求得∠COB的度数,然后根据角平分线的定义求得∠COD的度数.
【解答】解:∵OC是∠AOB的平分线,∠AOB=160°,
∴∠COB=∠AOB=80°,
又∵OD是∠COB的平分线,
∴∠COD=∠COB=40°.
【点评】本题考查了角平分线的定义,正确求得∠COB的度数是解题的关键.
21.如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=4∠COD,∠AOB=120°,求∠AOC的度数.
【分析】根据OD平分∠AOB可得出∠AOD=∠BOD,再由∠BOC=4∠COD可设∠COD=x,则∠BOD=3x,AOC=2x,再由∠AOB=120°可得出x的值,进而得出结论.
【解答】解:∵OD平分∠AOB,
∴∠AOD=∠BOD.
∵∠BOC=4∠COD,
∴设∠COD=x,则∠BOD=3x,AOC=2x,
∵∠AOB=120°,
∴2x+x+3x=120°,解得x=20°,
∴∠AOC=2x=40°.
【点评】本题考查的是角的计算,熟知角平分线的定义是解答此题的关键.
22.如图,已知∠AOB是直角,∠BOC在∠AOB的外部,且OF平分∠BOC,OE平分∠AOC.
(1)当∠BOC=60°时,求∠EOF的度数;
(2)当∠BOE=20°,求∠BOC的度数.
【分析】(1)利用角平分线的定义和角的和差的意义即可解答;
(2)由∠BOE=20°,可得∠AOE=70°,由角平分线的意义可得∠EOC=∠AOE=70°,则∠BOC=∠EOC﹣∠BOE.
【解答】解:(1)∠AOB是直角,∠BOC=60°,
∴∠AOC=∠AOB+∠BOC=150°.
∵OE平分∠AOC,
∴∠EOC=∠AOC=75°,
∵OF平分∠BOC,∠BOC=60°,
∴∠FOC=∠BOC=30°.
∴∠EOF=∠EOC﹣∠FOC=45°;
(2)∵∠BOE=20°,∠AOB是直角,
∴∠AOE=∠AOB﹣∠BOE=70°,
∵OE平分∠AOC,
∴∠AOE=∠EOC=70°,
∴∠BOC=∠EOC﹣∠BOE=70°﹣20°=50°.
【点评】本题主要考查了角的计算,角平分线的定义.充分利用图形中角的和差的意义与角平分线的定义是解题的关键.
23.如图,OE是∠COA的平分线,∠AOB=∠COD.
(1)若∠AOE=50°,∠COD=18°,求∠BOC的度数;
(2)比较∠AOC和∠BOD的大小,并说明理由.
【分析】(1)依据角平分线的定义,即可得到∠AOC的度数,再根据角的和差关系,即可得出∠BOC的度数;
(2)依据等式的性质,即可得到∠AOC=∠BOD.
【解答】解:(1)∵OE是∠COA的平分线,∠AOE=50°,
∴∠AOC=2∠AOE=100°,
又∵∠AOB=∠COD=18°,
∴∠BOC=∠AOC﹣∠AOB=100°﹣18°=82°;
(2)∠AOC=∠BOD.
理由:∵∠AOB=∠COD,
∴∠AOB+∠BOC=∠COD+∠BOC,
∴∠AOC=∠BOD.
【点评】本题主要考查了角的大小比较以及角平分线的定义的运用,从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
24.∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.
【分析】(1)利用角的和差定义证明即可;
(2)求出∠AOC即可解决问题;
(3)结论:∠AOD+∠COB=120°.利用角的和差定义证明即可;
(4)不成立.猜想:∠AOD+∠BOC=240°,根据周角的性质证明即可;
【解答】解:(1)结论:∠AOC=∠BOD.
理由:∵∠AOB=∠COD=60°,
∴∠AOC+∠BOC=∠BOD+∠BOC,
∴∠AOC=∠BOD.
(2)∵∠BCO=10°,∠AOB=60°,
∴∠AOC=50°,
∴∠AOD=∠AOC+∠COD=50°+60°=110°.
(3)猜想:∠AOD+∠COB=120°.
理由:∵∠AOB=∠COD=60°.
∴∠AOD=∠AOB+∠COD﹣∠COB=120°﹣∠COB,
∴∠AOD+∠COB=120°.
(4)不成立.猜想:∠AOD+∠BOC=240°,
理由:∵∠AOB=∠COD=60°.
∴∠AOD+∠BOC=360°﹣60°﹣60°=240°.
【点评】本题考查角的计算,角的和差定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考基础题.
