2021-2022学年人教版八年级数学上册12.2三角形全等的判定 同步练习 (word版、含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册12.2三角形全等的判定 同步练习 (word版、含答案) | 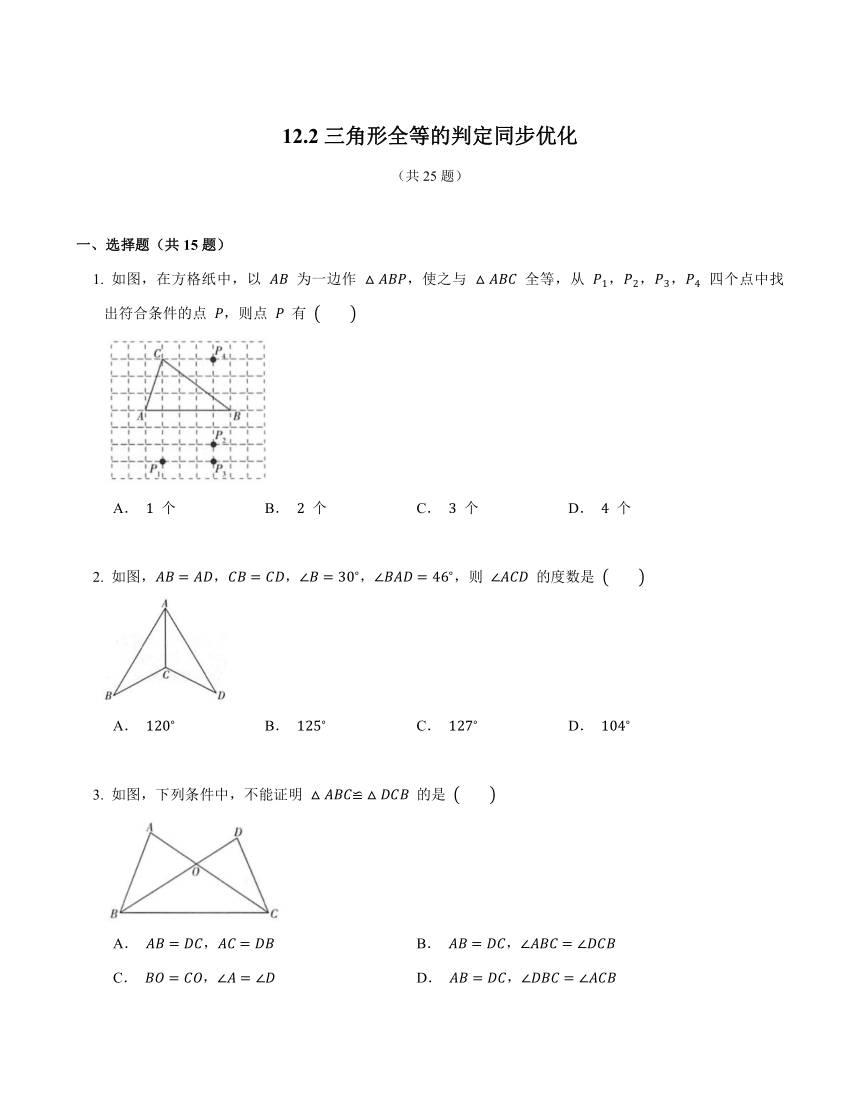 | |
| 格式 | docx | ||
| 文件大小 | 329.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 15:46:47 | ||
图片预览



文档简介
12.2三角形全等的判定同步优化
(共25题)
一、选择题(共15题)
如图,在方格纸中,以 为一边作 ,使之与 全等,从 ,,, 四个点中找出符合条件的点 ,则点 有
A. 个 B. 个 C. 个 D. 个
如图,,,,,则 的度数是
A. B. C. D.
如图,下列条件中,不能证明 的是
A. , B. ,
C. , D. ,
如图,已知 ,,增加下列条件:
① ;② ;
③ ;④ .
其中能使 的条件有
A. 个 B. 个 C. 个 D. 个
下列各组条件中,能判定 的是
A. ,,
B. ,,
C. ,, 的周长 的周长
D. ,,
如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是
A.带①去 B.带②去 C.带③去 D.带①和②去
如图,,,要使 ,需要添加下列选项中的
A. B. C. D.
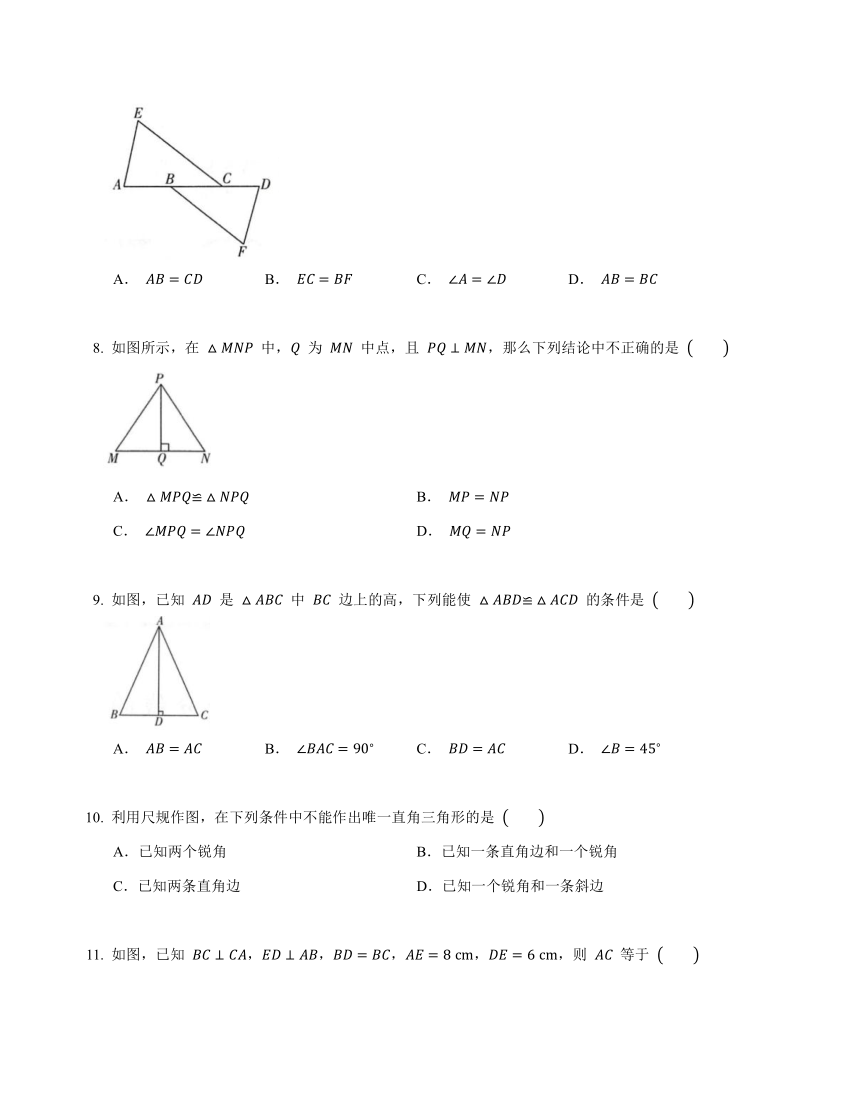
如图所示,在 中, 为 中点,且 ,那么下列结论中不正确的是
A. B.
C. D.
如图,已知 是 中 边上的高,下列能使 的条件是
A. B. C. D.
利用尺规作图,在下列条件中不能作出唯一直角三角形的是
A.已知两个锐角 B.已知一条直角边和一个锐角
C.已知两条直角边 D.已知一个锐角和一条斜边
如图,已知 ,,,,,则 等于
A. B. C. D.
如图,在 中,,, 是 边上的中线,则 的取值范围是
A. B. C. D.
如图,在下列各组条件中,能够判断 和 全等的有
① ,,;
② ,,;
③ ,,;
④ ,,.
A.①②③ B.①②④ C.①③④ D.②③④
如图,最适合用“”定理判定 和 全等的条件是
A. , B. ,
C. , D. ,
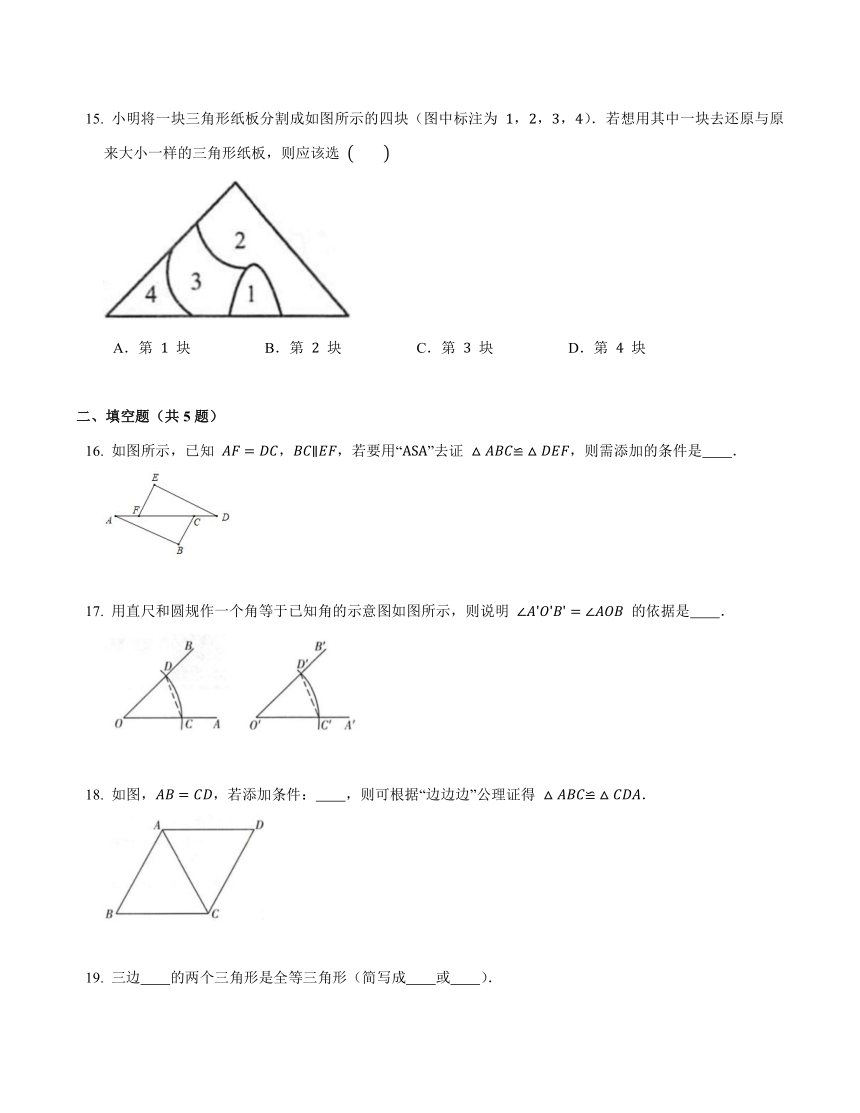
小明将一块三角形纸板分割成如图所示的四块(图中标注为 ,,,).若想用其中一块去还原与原来大小一样的三角形纸板,则应该选
A.第 块 B.第 块 C.第 块 D.第 块
二、填空题(共5题)
如图所示,已知 ,,若要用“”去证 ,则需添加的条件是 .
用直尺和圆规作一个角等于已知角的示意图如图所示,则说明 的依据是 .
如图,,若添加条件: ,则可根据“边边边”公理证得 .
三边 的两个三角形是全等三角形(简写成 或 ).
用几何语言表述:
在 和 中,
.
(注意:三角形的三边确定了,这个三角形的形状、大小也就确定了,这是三角形“”判定方法在三角形稳定性上的一个应用.)
两角和其中一角的对边对应相等的两个三角形全等(可以简写成“ ”或“ ”).
用几何语言表述如下:
在 和 中,
( ).
三、解答题(共5题)
如图,有一池塘,要测池塘两端 , 的距离,可先在平地上取一个点 ,从点 不经过池塘可以直接到达点 和 .连接 并延长到点 ,使 .连接 并延长到点 ,使 .连接 ,那么量出 的长就是 , 的距离.为什么?
如图,有一块三角形的土地,,,要把这块地平均分给甲、乙、丙三家农户,且他们所得土地的大小、形状都相同,请你试着分一分,在图上画出来.
已知:.
求作:,使 (作法参照教科书).
如图,,,.
求证:.
如图,在 中,, 是 的中点.
(1) 求证:.
(2) 求证:.
答案
一、选择题(共15题)
1. 【答案】C
2. 【答案】C
3. 【答案】D
4. 【答案】B
5. 【答案】C
6. 【答案】C
7. 【答案】A
8. 【答案】D
9. 【答案】A
10. 【答案】A
11. 【答案】C
12. 【答案】C
13. 【答案】A
14. 【答案】C
15. 【答案】B
二、填空题(共5题)
16. 【答案】
【解析】 ,
理由是:因为 ,
所以 ,
所以 ,
因为 ,
所以 ,
在 和 中,
所以 .
故答案为:.
17. 【答案】
18. 【答案】
19. 【答案】略;略;略;略;略;略;略
20. 【答案】略;略;略;略;略;略;略
三、解答题(共5题)
21. 【答案】连接 ,由题意:
在 与 中,
(),
,
即 的长就是 的距离.
22. 【答案】画图略,提示:作 的平分线 交 于点 ,再作 于点 ,则 .或:作边 的垂直平分线交 于点 ,交 于点 ,连接 .
23. 【答案】略.
24. 【答案】 ,
,即 ,
又 ,,
.
25. 【答案】
(1) 是 的中点,
.
在 和 中,
.
(2) ,
.
.
(共25题)
一、选择题(共15题)
如图,在方格纸中,以 为一边作 ,使之与 全等,从 ,,, 四个点中找出符合条件的点 ,则点 有
A. 个 B. 个 C. 个 D. 个
如图,,,,,则 的度数是
A. B. C. D.
如图,下列条件中,不能证明 的是
A. , B. ,
C. , D. ,
如图,已知 ,,增加下列条件:
① ;② ;
③ ;④ .
其中能使 的条件有
A. 个 B. 个 C. 个 D. 个
下列各组条件中,能判定 的是
A. ,,
B. ,,
C. ,, 的周长 的周长
D. ,,
如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是
A.带①去 B.带②去 C.带③去 D.带①和②去
如图,,,要使 ,需要添加下列选项中的
A. B. C. D.
如图所示,在 中, 为 中点,且 ,那么下列结论中不正确的是
A. B.
C. D.
如图,已知 是 中 边上的高,下列能使 的条件是
A. B. C. D.
利用尺规作图,在下列条件中不能作出唯一直角三角形的是
A.已知两个锐角 B.已知一条直角边和一个锐角
C.已知两条直角边 D.已知一个锐角和一条斜边
如图,已知 ,,,,,则 等于
A. B. C. D.
如图,在 中,,, 是 边上的中线,则 的取值范围是
A. B. C. D.
如图,在下列各组条件中,能够判断 和 全等的有
① ,,;
② ,,;
③ ,,;
④ ,,.
A.①②③ B.①②④ C.①③④ D.②③④
如图,最适合用“”定理判定 和 全等的条件是
A. , B. ,
C. , D. ,
小明将一块三角形纸板分割成如图所示的四块(图中标注为 ,,,).若想用其中一块去还原与原来大小一样的三角形纸板,则应该选
A.第 块 B.第 块 C.第 块 D.第 块
二、填空题(共5题)
如图所示,已知 ,,若要用“”去证 ,则需添加的条件是 .
用直尺和圆规作一个角等于已知角的示意图如图所示,则说明 的依据是 .
如图,,若添加条件: ,则可根据“边边边”公理证得 .
三边 的两个三角形是全等三角形(简写成 或 ).
用几何语言表述:
在 和 中,
.
(注意:三角形的三边确定了,这个三角形的形状、大小也就确定了,这是三角形“”判定方法在三角形稳定性上的一个应用.)
两角和其中一角的对边对应相等的两个三角形全等(可以简写成“ ”或“ ”).
用几何语言表述如下:
在 和 中,
( ).
三、解答题(共5题)
如图,有一池塘,要测池塘两端 , 的距离,可先在平地上取一个点 ,从点 不经过池塘可以直接到达点 和 .连接 并延长到点 ,使 .连接 并延长到点 ,使 .连接 ,那么量出 的长就是 , 的距离.为什么?
如图,有一块三角形的土地,,,要把这块地平均分给甲、乙、丙三家农户,且他们所得土地的大小、形状都相同,请你试着分一分,在图上画出来.
已知:.
求作:,使 (作法参照教科书).
如图,,,.
求证:.
如图,在 中,, 是 的中点.
(1) 求证:.
(2) 求证:.
答案
一、选择题(共15题)
1. 【答案】C
2. 【答案】C
3. 【答案】D
4. 【答案】B
5. 【答案】C
6. 【答案】C
7. 【答案】A
8. 【答案】D
9. 【答案】A
10. 【答案】A
11. 【答案】C
12. 【答案】C
13. 【答案】A
14. 【答案】C
15. 【答案】B
二、填空题(共5题)
16. 【答案】
【解析】 ,
理由是:因为 ,
所以 ,
所以 ,
因为 ,
所以 ,
在 和 中,
所以 .
故答案为:.
17. 【答案】
18. 【答案】
19. 【答案】略;略;略;略;略;略;略
20. 【答案】略;略;略;略;略;略;略
三、解答题(共5题)
21. 【答案】连接 ,由题意:
在 与 中,
(),
,
即 的长就是 的距离.
22. 【答案】画图略,提示:作 的平分线 交 于点 ,再作 于点 ,则 .或:作边 的垂直平分线交 于点 ,交 于点 ,连接 .
23. 【答案】略.
24. 【答案】 ,
,即 ,
又 ,,
.
25. 【答案】
(1) 是 的中点,
.
在 和 中,
.
(2) ,
.
.
