4.2.3 线段的性质及其应用 课件(共20张PPT)
文档属性
| 名称 | 4.2.3 线段的性质及其应用 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
4.2 直线、射线、线段
第3课时 线段的性质及其应用
人教版七年级数学上册 ·上课课件
第四章 几何图形初步
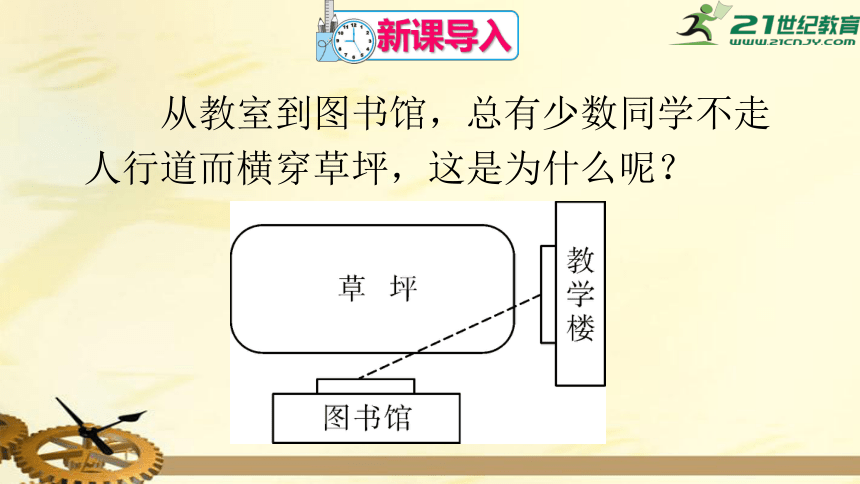
新课导入
从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?
两点之间,线段最短.
为什么两点之间线段最短呢?本课我们继续探讨线段的有关性质.
学习目标
一、教学目标
1.知道中点和三等分点的含义,会画中点和三等分点.
2.经历发现两点之间线段最短结论的过程,知道两点距离的含义.知道“两点之间,线段最短”的性质及“两点间的距离”的意义.
二、教学重点和难点
1.重点:中点、三等分点、两点距离的概念,两点之间线段最短的结论.
2.难点:几何语言的表述.
推进新课
线段的性质及其应用
知识点
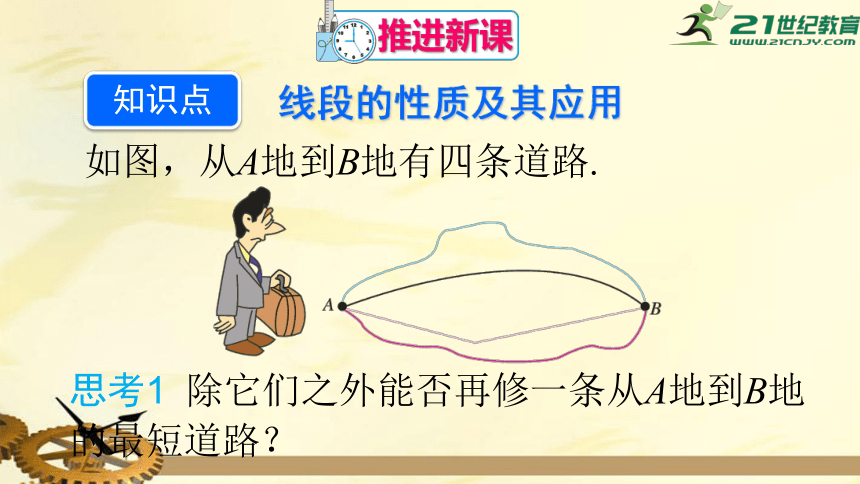
如图,从A地到B地有四条道路.
思考1 除它们之外能否再修一条从A地到B地的最短道路?
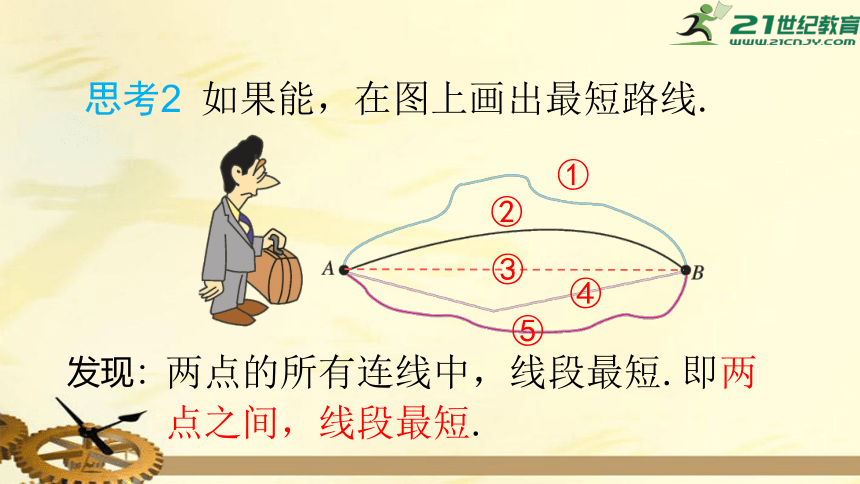
思考2 如果能,在图上画出最短路线.
两点的所有连线中,线段最短.即两点之间,线段最短.
发现:
①
②
③
④
⑤
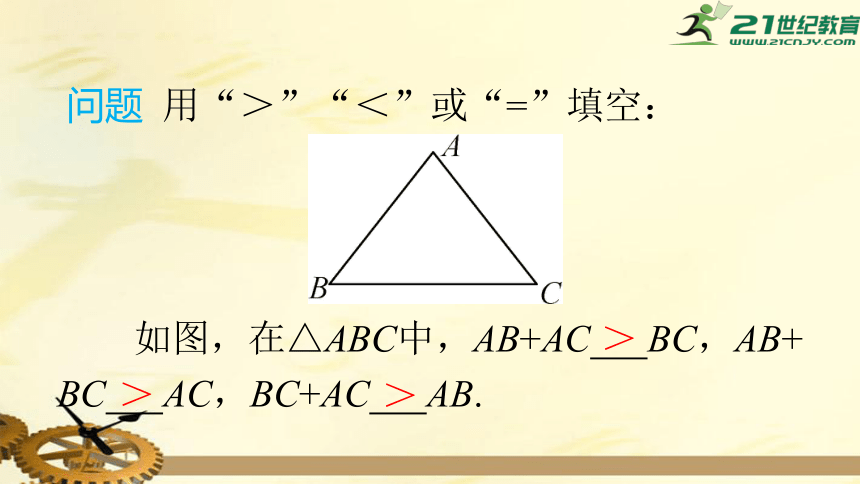
问题 用“>”“<”或“=”填空:
如图,在△ABC中,AB+AC BC,AB+
BC AC,BC+AC AB.
>
>
>
问题 你能举例说明“两点之间,线段最短”的实际应用吗?与同学们交流一下.
1
道路会尽可能修直一点.
3
人们为了走捷径,有时会横穿马路.
2
小狗看见骨头会径直跑过去.
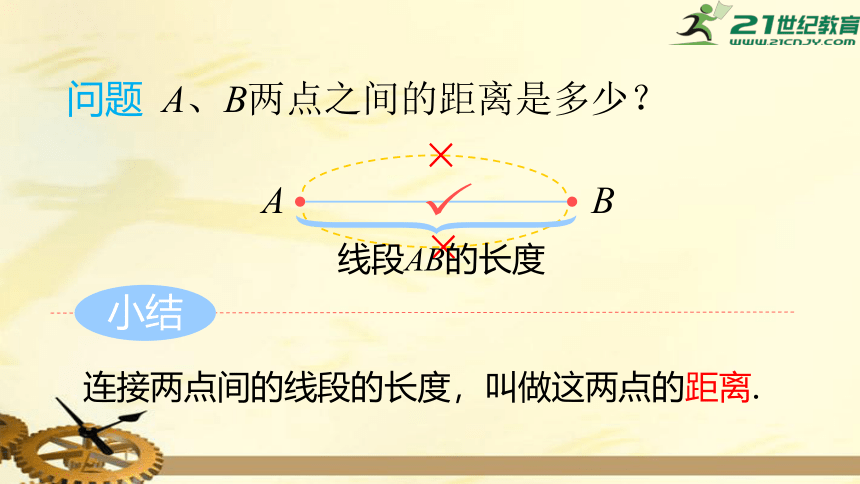
连接两点间的线段的长度,叫做这两点的距离.
问题 A、B两点之间的距离是多少?
A
B
小结
×
×
线段AB的长度
强化练习
1.把弯曲的河道改直,能够缩短航程,这
样做的道理是( )
A.两点之间,射线最短
B.两点确定一条直线
C.两点之间,线段最短
D.两点之间,直线最短
C
强化练习
2.如图,从A出发到B时,最近的路是( )
A. A→C→D→B
B. A→C→F→E→B
C. A→C→E→B
D. A→C→G→B
C
随堂演练
1.已知A、B、C三点在同一直线上,如果
线段AB=6 cm,BC=3 cm,A、C两点的
距离为d,那么( )
A.d=9cm B.d=3cm
C.d=9cm或d=3cm D.d大小不确定
C
2.如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?如果要爬行到顶点C呢?说出你的理由.
沿AB连线爬行最短.
解:如果要爬行到顶点C,有三种
情况:若蚂蚁爬行时经过面AD,
可将这个正方体展开,在展开图
上连接AC,与棱a(或b)交于D1(或
D2),蚂蚁沿AD1→D1C(或AD2→D2C)爬行,路线最短.类似地,蚂蚁经过面AB和AE爬行到顶点C,也分别有两条最短路线,因此,蚂蚁爬行的最短路线有6条.
课堂小结
两点的所有连线中,线段最短.即两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
两点之间线段最短这一性质是度量的基础,在生产实际中经常要用到,这节课主要是让学生体验两点之间线段最短这一性质以及两点间距离的概念.经历从具体事例抽象出性质,再根据性质应用到具体事例的活动过程,体会从具体到抽象,再由抽象到具体的辩证关系.
教科书分层次的安排了这些内容,本节课学生只要能根据具体事例判断能否利用两点之间线段最短这一性质,以及利用这一性质进行规划设计即可.此外,两点间距离的概念,学生一般也容易理解.本节课的目的是通过学习,进
教学反思
一步发展学生的空间观念,学生逐渐形成对空间图形与平面图形的认识与区别,体会现实生活中处处有图形,处处有数学.
在这一课教与学的过程中,教师应积极渗透自主学习探索、合作交流、实践创新的学习理念,通过对内容的挖掘与整理,采用“问题情境——建立模型——解释、应用与拓展”的模式展开教学,让学生经历“从生活中发现数学——在教室里学习数学——到生活中运用数学”这一个过程,从而更好地理解数学知识的意义,发展应用数学知识的意识与能力,进一步增强学好数学的愿望和信心.
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
4.2 直线、射线、线段
第3课时 线段的性质及其应用
人教版七年级数学上册 ·上课课件
第四章 几何图形初步
新课导入
从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?
两点之间,线段最短.
为什么两点之间线段最短呢?本课我们继续探讨线段的有关性质.
学习目标
一、教学目标
1.知道中点和三等分点的含义,会画中点和三等分点.
2.经历发现两点之间线段最短结论的过程,知道两点距离的含义.知道“两点之间,线段最短”的性质及“两点间的距离”的意义.
二、教学重点和难点
1.重点:中点、三等分点、两点距离的概念,两点之间线段最短的结论.
2.难点:几何语言的表述.
推进新课
线段的性质及其应用
知识点
如图,从A地到B地有四条道路.
思考1 除它们之外能否再修一条从A地到B地的最短道路?
思考2 如果能,在图上画出最短路线.
两点的所有连线中,线段最短.即两点之间,线段最短.
发现:
①
②
③
④
⑤
问题 用“>”“<”或“=”填空:
如图,在△ABC中,AB+AC BC,AB+
BC AC,BC+AC AB.
>
>
>
问题 你能举例说明“两点之间,线段最短”的实际应用吗?与同学们交流一下.
1
道路会尽可能修直一点.
3
人们为了走捷径,有时会横穿马路.
2
小狗看见骨头会径直跑过去.
连接两点间的线段的长度,叫做这两点的距离.
问题 A、B两点之间的距离是多少?
A
B
小结
×
×
线段AB的长度
强化练习
1.把弯曲的河道改直,能够缩短航程,这
样做的道理是( )
A.两点之间,射线最短
B.两点确定一条直线
C.两点之间,线段最短
D.两点之间,直线最短
C
强化练习
2.如图,从A出发到B时,最近的路是( )
A. A→C→D→B
B. A→C→F→E→B
C. A→C→E→B
D. A→C→G→B
C
随堂演练
1.已知A、B、C三点在同一直线上,如果
线段AB=6 cm,BC=3 cm,A、C两点的
距离为d,那么( )
A.d=9cm B.d=3cm
C.d=9cm或d=3cm D.d大小不确定
C
2.如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?如果要爬行到顶点C呢?说出你的理由.
沿AB连线爬行最短.
解:如果要爬行到顶点C,有三种
情况:若蚂蚁爬行时经过面AD,
可将这个正方体展开,在展开图
上连接AC,与棱a(或b)交于D1(或
D2),蚂蚁沿AD1→D1C(或AD2→D2C)爬行,路线最短.类似地,蚂蚁经过面AB和AE爬行到顶点C,也分别有两条最短路线,因此,蚂蚁爬行的最短路线有6条.
课堂小结
两点的所有连线中,线段最短.即两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
两点之间线段最短这一性质是度量的基础,在生产实际中经常要用到,这节课主要是让学生体验两点之间线段最短这一性质以及两点间距离的概念.经历从具体事例抽象出性质,再根据性质应用到具体事例的活动过程,体会从具体到抽象,再由抽象到具体的辩证关系.
教科书分层次的安排了这些内容,本节课学生只要能根据具体事例判断能否利用两点之间线段最短这一性质,以及利用这一性质进行规划设计即可.此外,两点间距离的概念,学生一般也容易理解.本节课的目的是通过学习,进
教学反思
一步发展学生的空间观念,学生逐渐形成对空间图形与平面图形的认识与区别,体会现实生活中处处有图形,处处有数学.
在这一课教与学的过程中,教师应积极渗透自主学习探索、合作交流、实践创新的学习理念,通过对内容的挖掘与整理,采用“问题情境——建立模型——解释、应用与拓展”的模式展开教学,让学生经历“从生活中发现数学——在教室里学习数学——到生活中运用数学”这一个过程,从而更好地理解数学知识的意义,发展应用数学知识的意识与能力,进一步增强学好数学的愿望和信心.
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
