4.2.2 线段的比较与度量 课件(共25张PPT)
文档属性
| 名称 | 4.2.2 线段的比较与度量 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 10:18:55 | ||
图片预览








文档简介
(共25张PPT)
4.2 直线、射线、线段
第2课时 线段的比较与度量
人教版七年级数学上册 ·上课课件
第四章 几何图形初步
新课导入
上节课我们学习了直线、射线、线段的概念和表示方法,这节课来学习线段的大小比较,线段的和、差、倍、分.
学习目标
【知识与技能】
1.结合图形认识线段间的数量关系,学会比较线段的大小.
2.知道两点之间的距离和线段中点的含义.
【过程与方法】
利用丰富的活动情景,让学生体验到两点之间线段最短的性质,并能初步应用.
【情感态度】
初步应用空间与图形的知识解释生活中的现象以及解决简单的实际问题,体会研究几何图形的意义.
【教学重点】
线段大小比较,线段的性质.
【教学难点】
线段中点、三等分点、四等分点的表示方法及运用.
推进新课
作线段等于已知线段
知识点1
问题 如图,已知线段a,你可以画出一条同样大小的线段来吗?用什么方法呢?
a
a
度量法:用刻度尺量出已知线段,再画一条与它相等的线段.
a
A C
a
B
b
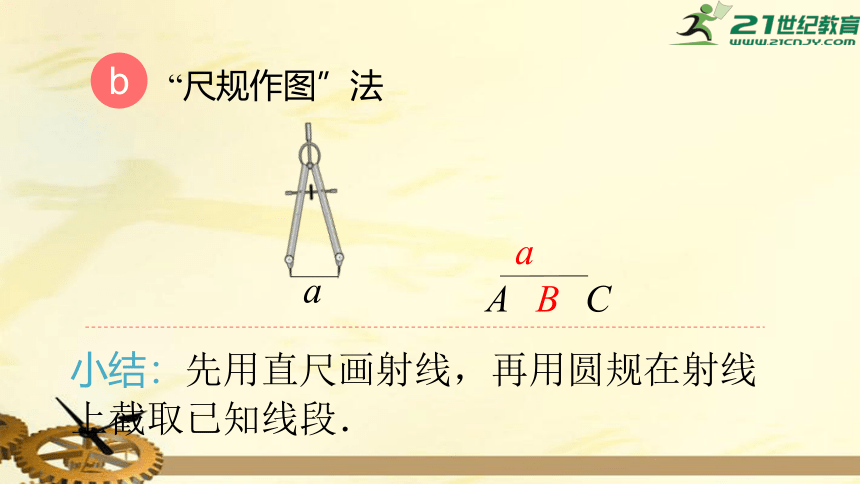
“尺规作图”法
小结:先用直尺画射线,再用圆规在射线上截取已知线段.
问题 黑板上有两条线段,你能判断一下它们的长短吗?你用的什么方法?
a
度量法:即用刻度尺分别量出它们的长度,然后比较它们的长度的大小.
a
b
A B
C D
(A)
B
b
叠合法
记作 AB<CD
线段AB小于线段CD
1
2
两条线段要放在同一条直线上.
一个端点重合,另一个端点要放在公共端点的同侧.
用叠合法比较线段的长短时,有什么需要注意的吗?
思考
强化练习
1.判断线段 AB和CD的大小.
AB>CD
A(C)
D
B
A(C)
B
D
A(C)
B(D)
AB=CD
AB<CD
两条线段的和、差、倍、分
知识点2
问题 如图,已知线段 a 和 b,且 a>b.
a
b
a. AB=a,BC=b,则线段AC就是a与b的 .
记作 .
A B C
和
AC=a+b
问题 如图,已知线段 a 和 b,且 a>b.
a
b
b. AB=a,BD=b,则线段AD就是a与b的 .
记作 .
A B
差
AD=a-b
D
问题 如图,已知线段a和线段b,怎样通过作图得到a与b的和、a与b的差呢?
b
a
B
C
a
b
A
P
B
C
a
b
A
P
AC=a+b
CB=a-b
问题 如图,已知线段a,求作线段AC=2a.
a
M
C
a
A
P
AC=2a
a
思考 线段AC的中点是什么?
M
C
a
A
P
a
点 M 把线段 AC 分成相等的两条线段AM与MC,点 M 叫做线段 AC 的中点,可知 AM=MC= AC.
1
2
思考 那么什么叫做三等分点?四等分点呢?
a
三等分点
如图,若点M、N是线段AB的三等分点,
则AM = = = ,反过来也成立.
MN
NB
AB
1
3
b
四等分点
如图,若点M、N、P是线段AB的四等分
点,则AM = = = = ,反过来也成立.
MN
NP
AB
1
4
PB
强化练习
1.如图,点 D 是线段 AB 的中点,C 是线段 AD的中点,若 AB =4cm,求线段 CD 的长度.
随堂演练
1.如图,已知线段a、b、c,用圆规和直尺作线段,使它等于a+2b-c.
解:作射线AB,在射线AB上截取线段AC=a+
2b,在线段CA上截取线段CE=c,则线段AE为求作的线段.
2.两条直线相交,有一个交点,三条直线相交最多有多少个交点?四条直线呢?你能发现什么规律吗?
1
3=1+2
6=1+2+3
解:三条直线相交最多有1+2=3个交点,四条直线相交最多有1+2+3=6个交点,我们可以发现,n条直线相交最多有(1+2+3+4+
……+n-1)个交点,也就是 个交点,此处n≥3且n为自然数.
课堂小结
线段的比较
两条线段的和、差、倍、分
度量法
叠合法
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
本节教学应通过问题启发、做、想、试等方式,让学生主动探索来认识知识,在学生自己动手实践、小组合作的基础上,在实践中体验线段的大小比较.从比较身高的具体活动中抽象出线段比较的方法,这样的教学,可使学生得到探索发现的成功感,自然获取知识形成应用能力.
教学反思
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
4.2 直线、射线、线段
第2课时 线段的比较与度量
人教版七年级数学上册 ·上课课件
第四章 几何图形初步
新课导入
上节课我们学习了直线、射线、线段的概念和表示方法,这节课来学习线段的大小比较,线段的和、差、倍、分.
学习目标
【知识与技能】
1.结合图形认识线段间的数量关系,学会比较线段的大小.
2.知道两点之间的距离和线段中点的含义.
【过程与方法】
利用丰富的活动情景,让学生体验到两点之间线段最短的性质,并能初步应用.
【情感态度】
初步应用空间与图形的知识解释生活中的现象以及解决简单的实际问题,体会研究几何图形的意义.
【教学重点】
线段大小比较,线段的性质.
【教学难点】
线段中点、三等分点、四等分点的表示方法及运用.
推进新课
作线段等于已知线段
知识点1
问题 如图,已知线段a,你可以画出一条同样大小的线段来吗?用什么方法呢?
a
a
度量法:用刻度尺量出已知线段,再画一条与它相等的线段.
a
A C
a
B
b
“尺规作图”法
小结:先用直尺画射线,再用圆规在射线上截取已知线段.
问题 黑板上有两条线段,你能判断一下它们的长短吗?你用的什么方法?
a
度量法:即用刻度尺分别量出它们的长度,然后比较它们的长度的大小.
a
b
A B
C D
(A)
B
b
叠合法
记作 AB<CD
线段AB小于线段CD
1
2
两条线段要放在同一条直线上.
一个端点重合,另一个端点要放在公共端点的同侧.
用叠合法比较线段的长短时,有什么需要注意的吗?
思考
强化练习
1.判断线段 AB和CD的大小.
AB>CD
A(C)
D
B
A(C)
B
D
A(C)
B(D)
AB=CD
AB<CD
两条线段的和、差、倍、分
知识点2
问题 如图,已知线段 a 和 b,且 a>b.
a
b
a. AB=a,BC=b,则线段AC就是a与b的 .
记作 .
A B C
和
AC=a+b
问题 如图,已知线段 a 和 b,且 a>b.
a
b
b. AB=a,BD=b,则线段AD就是a与b的 .
记作 .
A B
差
AD=a-b
D
问题 如图,已知线段a和线段b,怎样通过作图得到a与b的和、a与b的差呢?
b
a
B
C
a
b
A
P
B
C
a
b
A
P
AC=a+b
CB=a-b
问题 如图,已知线段a,求作线段AC=2a.
a
M
C
a
A
P
AC=2a
a
思考 线段AC的中点是什么?
M
C
a
A
P
a
点 M 把线段 AC 分成相等的两条线段AM与MC,点 M 叫做线段 AC 的中点,可知 AM=MC= AC.
1
2
思考 那么什么叫做三等分点?四等分点呢?
a
三等分点
如图,若点M、N是线段AB的三等分点,
则AM = = = ,反过来也成立.
MN
NB
AB
1
3
b
四等分点
如图,若点M、N、P是线段AB的四等分
点,则AM = = = = ,反过来也成立.
MN
NP
AB
1
4
PB
强化练习
1.如图,点 D 是线段 AB 的中点,C 是线段 AD的中点,若 AB =4cm,求线段 CD 的长度.
随堂演练
1.如图,已知线段a、b、c,用圆规和直尺作线段,使它等于a+2b-c.
解:作射线AB,在射线AB上截取线段AC=a+
2b,在线段CA上截取线段CE=c,则线段AE为求作的线段.
2.两条直线相交,有一个交点,三条直线相交最多有多少个交点?四条直线呢?你能发现什么规律吗?
1
3=1+2
6=1+2+3
解:三条直线相交最多有1+2=3个交点,四条直线相交最多有1+2+3=6个交点,我们可以发现,n条直线相交最多有(1+2+3+4+
……+n-1)个交点,也就是 个交点,此处n≥3且n为自然数.
课堂小结
线段的比较
两条线段的和、差、倍、分
度量法
叠合法
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
本节教学应通过问题启发、做、想、试等方式,让学生主动探索来认识知识,在学生自己动手实践、小组合作的基础上,在实践中体验线段的大小比较.从比较身高的具体活动中抽象出线段比较的方法,这样的教学,可使学生得到探索发现的成功感,自然获取知识形成应用能力.
教学反思
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
