2021-2022学年鲁教版(五四制)七年级数学上册4.2平方根 同步达标测评(word版、含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学上册4.2平方根 同步达标测评(word版、含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 130.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 00:00:00 | ||
图片预览



文档简介
2021-2022学年鲁教版七年级数学上册《4.2平方根》同步达标测评(附答案)
一.选择题(共9小题,满分27分)
1.下列说法中正确的有( )
①0的算术平方根是0;
②8的算术平方根是4;
③±是11的平方根;
④﹣5是25的平方根;
⑤±2是8的平方根;
A.1个 B.2个 C.3个 D.4个
2.的算术平方根是多少( )
A.±4 B.2 C.±2 D.4
3.若x2=9,则x的值是( )
A.3 B.±3 C.81 D.±81
4.下列语句中正确的是( )
A.16的平方根是4 B.﹣16的平方根是4
C.16的算术平方根是±4 D.16的算术平方根是4
5.下列说法不正确的是( )
A.21的平方根是±
B.的平方根是
C.0.01的算术平方根是0.1
D.﹣5是25的一个平方根
6.有一个边长为9cm的正方形和一个长为24cm,宽为6cm的长方形,作一个面积为这两个图形的面积之和的正方形,则该正方形的边长为( )
A.15cm B.10cm C.5cm D.25cm
7.下列说法正确的是( )
A.4的平方根是2 B.的平方根是±4
C.25的平方根是±5 D.﹣36的算术平方根是6
8.下列计算正确的是( )
A.=﹣2 B.=3 C.±=±4 D.=2
9.的平方根是( )
A.9 B.9和﹣9 C.3 D.3和﹣3
二.填空题(共12小题,满分36分)
10.实数的平方根是 .
11.若﹣是m的一个平方根,则m+13的算术平方根是 .
12.若数x﹣2的平方根只有一个,则x的值是 .
13.一个正数的两个平方根是2a+1和4﹣3a,则a= .
14.已知一个数的两个平方根分别是2a+4和a+14,则这个数是 .
15.25的算术平方根为x,4是y+1的一个平方根,则x﹣y= .
16.若m+=5,则= .
17.的算术平方根是 .
18.如果一个正方形的面积为3,则这个正方形的边长是 .
19.a﹣1与3﹣2a是某正数的两个平方根,则实数a的值是 .
20.已知某数的一个平方根是,那么它的另一个平方根是 .
21.如果=3,那么m的值是 .
三.解答题(共6小题,满分57分)
22.已知一个数m的两个不相等的平方根分别为a+2和3a﹣18.
(1)求a的值;
(2)求这个数m.
23.已知(a+3)2+,求(a+b)c的值.
24.喜欢探索数学知识的小明遇到一个新的定义:对于三个互不相等的正整数,若其中任意两个数乘积的算术平方根都是整数,则称这三个数为“老根数”,其结果中最小的整数称为“最小算术平方根”,最大的整数称为“最大算术平方根”.例如:1,4,9这三个数,=2,=3,=6,其结果分别为2,3,6都是整数,所以1,4,9这三个数称为“老根数”,其中“最小算术平方根”是2,“最大算术平方根”是6.
(1)请证明:2,8,50这三个数是“老根数”,并求出任意两个数乘积的最小算术平方根与最大算术平方根;
(2)已知16,a,36,这三个数是“老根数”,且任意两个数乘积的算术平方根中,最大算术平方根是最小算术平方根的2倍,求a的值.
25.根据表回答问题:
x 16 16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8 16.9 17
y 256 259.21 262.44 265.69 268.96 272.25 275.56 278.89 282.24 285.61 289
(1)= ;≈ .
(2)272.25的平方根是 ;
(3)若a,b是表中两个相邻的数,a<<b,则a= ,b= .
26.已知x=1﹣2a,y=3a﹣4.
(1)已知x的算术平方根为3,求a的值;
(2)如果一个正数的平方根分别为x,y,求这个正数.
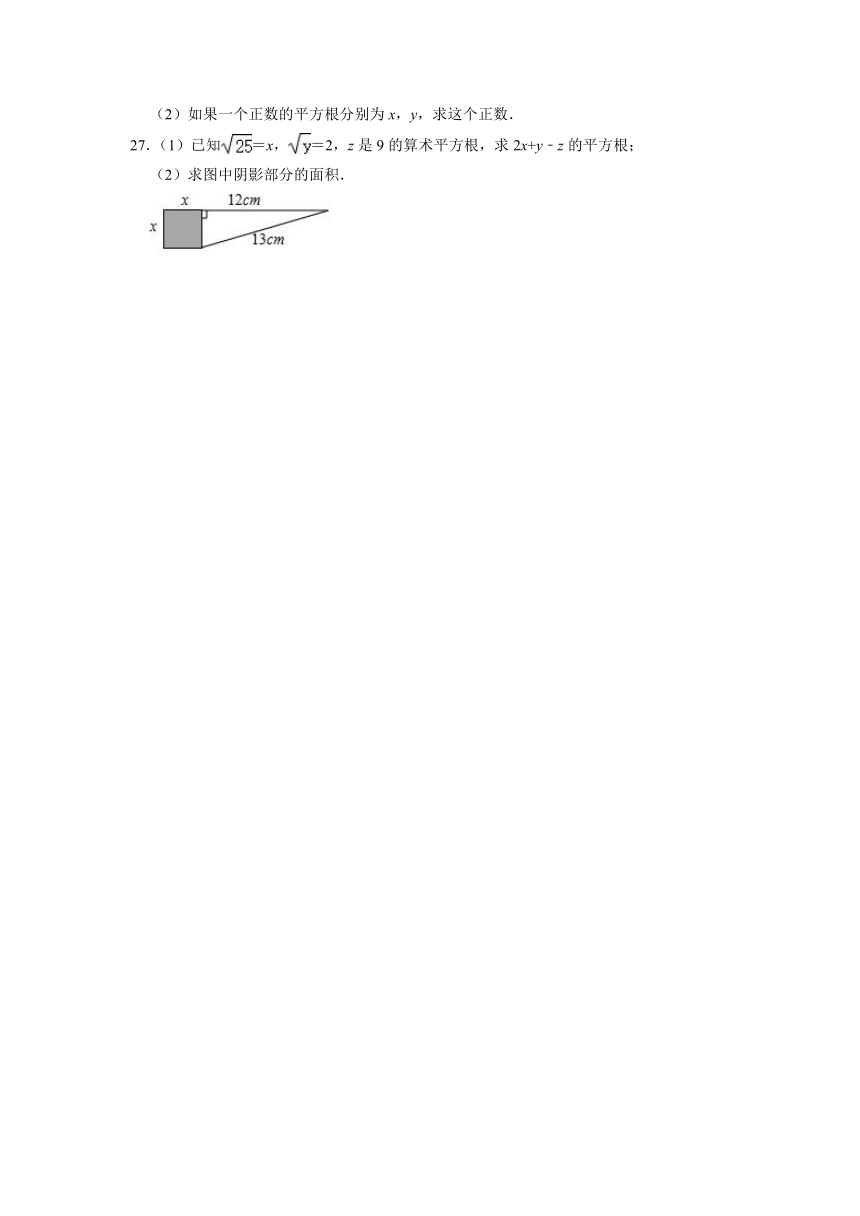
27.(1)已知=x,=2,z是9的算术平方根,求2x+y﹣z的平方根;
(2)求图中阴影部分的面积.
参考答案
一.选择题(共9小题,满分27分)
1.解:①根据算术平方根的定义,0的算术平方根是0,所以①说法正确;
②根据算术平方根的定义,8的算术平方根是2,所以②说法错误;
③根据平方根的定义,±是11的平方根,所以③说法正确;
④根据平方根的定义,﹣5是25的一个平方根,所以④说法正确.
⑤根据平方根的定义,±是8的平方根,所以⑤说法不正确.
综上:说法正确的有①③④,共3个.
故选:C.
2.解:=4,4的算术平方根是2.
故选:B.
3.解:由题意可得:x=±3.
故选:B.
4.解:A、16的平方根是±4,原说法错误,故此选项不符合题意;
B、﹣16没有平方根,原说法错误,故此选项不符合题意;
C、16的算术平方根是4,原说法错误,故此选项不符合题意;
D、16的算术平方根是4,原说法正确,故此选项符合题意.
故选:D.
5.解:A.21的平方根是,正确,故选项不符合题意;
B. 的平方根是,原说法错误.故选项符合题意;
C.0.01的算术平方根是0.1,正确,故选项不符合题意;
D.﹣5是25的一个平方根,正确,故选项不符合题意;
故选:B.
6.解:所作的正方形的面积为9×9+24×6=225(cm2),
所以所作的正方形的边长为=15(cm),
故选:A.
7.解:∵一个非0的数的平方根有两个,算术平方根有一个,
∴4的平方根是±2,
∴A选项不合题意,
∵=4,4的平方根是±2,
∴B选项不合题意,
∵25的平方根是±5,
∴C选项符合题意,
∵负数没有平方根,
∴D选项不合题意,
故选:C.
8.解:A.负数没有算术平方根,故A选项不符合题意;
B.,故B选项符合题意;
C.,故C选项不符合题意;
D.,故D选项不符合题意.
故选:B.
9.解:=9,
9的平方根为±=±3,
故选:D.
二.填空题(共12小题,满分36分)
10.解:∵=9,
∴实数的平方根是±=±3.
故答案为:±3.
11.解:根据题意得:m=(﹣)2=3,
则m+13=16,
因为16的算术平方根为4,
所以m+13的算术平方根是4.
故答案为:4.
12.解:∵平方根只有一个的数是0,
∴x﹣2=0,
∴x=2.
故答案为:2.
13.解:根据题意得:2a+1+4﹣3a=0,
解得:a=5.
故答案为:5.
14.解:∵一个数的两个平方根分别是2a+4和a+14,
∴(2a+4)+(a+14)=0,
解得a=﹣6,
a+14=﹣6+14=8,
8的平方是64.
故这个数是64.
故答案为:64.
15.解:25的算术平方根为=5,即x=5,
∵4是y+1的一个平方根,
∴y+1=16,即y=15,
∴x﹣y=5﹣15=﹣10,
故答案为:﹣10.
16.解:根据二次根式有意义的条件得:m﹣5≥0,
∴m≥5,
根据条件得:=5﹣m,
根据算术平方根的非负性得:5﹣m≥0,
∴m≤5,
∴m=5,
∴===3,
故答案为:3.
17.解:=0.09,
0.09的算术平方根是0.3.
故答案为:0.3.
18.解:设这个正方形的边长为x(x>0).
由题意得:x2=3.
∴x=.
故答案为:.
19.解:由题意得:a﹣1+3﹣2a=0.
∴a=2.
故答案为:2.
20.解:若一个数的一个平方根是,则它的另一个平方根是﹣.
故答案为:﹣.
21.解:∵32=9,
∴=3,
故答案为:9.
三.解答题(共6小题,满分57分)
22.解:(1)∵数m的两个不相等的平方根为a+2和3a﹣18,
∴(a+2)+(3a﹣18)=0,
∴4a=16,
解得a=4;
(2)∴a+2=4+2=6,3a﹣18=3×4﹣18=﹣6,
∴m=(±6)2=36,
∴m的值是36.
23.解:∵(a+3)2+,
∴a+3=0,b﹣2=0,c﹣2021=0,
解得:a=﹣3,b=2,c=2021.
∴(a+b)c=(﹣3+2)2021=﹣1.
24.(1)证明:因为=4,=10,=20,
所以2,8,50这三个数是“老根数”;
其中最小算术平方根是4,最大算术平方根是20;
(2)解:当a<16时,则2=,
解得a=9,
当16<a<36时,则2=,解得a=0,不合题意舍去;
当a>36时,则2=,
解得a=64,
综上所述,a=9或a=64.
25.解:(1)由表可得:,;
故答案为:16,16;
(2)由表可得:272.25的平方根为:;
故答案为:±16.5;
(3)∵a,b是表中两个相邻的数,a<<b,
∴a=16.7,b=16.8.
故答案为:16.7,16.8.
26.解:(1)∵x的算术平方根为3,
∴x=32=9,
即1﹣2a=9,
∴a=﹣4;
(2)根据题意得:x+y=0,
即:1﹣2a+3a﹣4=0,
∴a=3,
∴x=1﹣2a=1﹣2×3=1﹣6=﹣5,
∴这个正数为(﹣5)2=25.
27.解:(1)∵=x,=2,z是9的算术平方根,
∴x=5,y=4,z=3,
∴2x+y﹣z=2×5+4﹣3=11,
∴2x+y﹣z的平方根是±.
(2)x2=132﹣122=25(cm2),
图中阴影部分的面积是25cm2.
一.选择题(共9小题,满分27分)
1.下列说法中正确的有( )
①0的算术平方根是0;
②8的算术平方根是4;
③±是11的平方根;
④﹣5是25的平方根;
⑤±2是8的平方根;
A.1个 B.2个 C.3个 D.4个
2.的算术平方根是多少( )
A.±4 B.2 C.±2 D.4
3.若x2=9,则x的值是( )
A.3 B.±3 C.81 D.±81
4.下列语句中正确的是( )
A.16的平方根是4 B.﹣16的平方根是4
C.16的算术平方根是±4 D.16的算术平方根是4
5.下列说法不正确的是( )
A.21的平方根是±
B.的平方根是
C.0.01的算术平方根是0.1
D.﹣5是25的一个平方根
6.有一个边长为9cm的正方形和一个长为24cm,宽为6cm的长方形,作一个面积为这两个图形的面积之和的正方形,则该正方形的边长为( )
A.15cm B.10cm C.5cm D.25cm
7.下列说法正确的是( )
A.4的平方根是2 B.的平方根是±4
C.25的平方根是±5 D.﹣36的算术平方根是6
8.下列计算正确的是( )
A.=﹣2 B.=3 C.±=±4 D.=2
9.的平方根是( )
A.9 B.9和﹣9 C.3 D.3和﹣3
二.填空题(共12小题,满分36分)
10.实数的平方根是 .
11.若﹣是m的一个平方根,则m+13的算术平方根是 .
12.若数x﹣2的平方根只有一个,则x的值是 .
13.一个正数的两个平方根是2a+1和4﹣3a,则a= .
14.已知一个数的两个平方根分别是2a+4和a+14,则这个数是 .
15.25的算术平方根为x,4是y+1的一个平方根,则x﹣y= .
16.若m+=5,则= .
17.的算术平方根是 .
18.如果一个正方形的面积为3,则这个正方形的边长是 .
19.a﹣1与3﹣2a是某正数的两个平方根,则实数a的值是 .
20.已知某数的一个平方根是,那么它的另一个平方根是 .
21.如果=3,那么m的值是 .
三.解答题(共6小题,满分57分)
22.已知一个数m的两个不相等的平方根分别为a+2和3a﹣18.
(1)求a的值;
(2)求这个数m.
23.已知(a+3)2+,求(a+b)c的值.
24.喜欢探索数学知识的小明遇到一个新的定义:对于三个互不相等的正整数,若其中任意两个数乘积的算术平方根都是整数,则称这三个数为“老根数”,其结果中最小的整数称为“最小算术平方根”,最大的整数称为“最大算术平方根”.例如:1,4,9这三个数,=2,=3,=6,其结果分别为2,3,6都是整数,所以1,4,9这三个数称为“老根数”,其中“最小算术平方根”是2,“最大算术平方根”是6.
(1)请证明:2,8,50这三个数是“老根数”,并求出任意两个数乘积的最小算术平方根与最大算术平方根;
(2)已知16,a,36,这三个数是“老根数”,且任意两个数乘积的算术平方根中,最大算术平方根是最小算术平方根的2倍,求a的值.
25.根据表回答问题:
x 16 16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8 16.9 17
y 256 259.21 262.44 265.69 268.96 272.25 275.56 278.89 282.24 285.61 289
(1)= ;≈ .
(2)272.25的平方根是 ;
(3)若a,b是表中两个相邻的数,a<<b,则a= ,b= .
26.已知x=1﹣2a,y=3a﹣4.
(1)已知x的算术平方根为3,求a的值;
(2)如果一个正数的平方根分别为x,y,求这个正数.
27.(1)已知=x,=2,z是9的算术平方根,求2x+y﹣z的平方根;
(2)求图中阴影部分的面积.
参考答案
一.选择题(共9小题,满分27分)
1.解:①根据算术平方根的定义,0的算术平方根是0,所以①说法正确;
②根据算术平方根的定义,8的算术平方根是2,所以②说法错误;
③根据平方根的定义,±是11的平方根,所以③说法正确;
④根据平方根的定义,﹣5是25的一个平方根,所以④说法正确.
⑤根据平方根的定义,±是8的平方根,所以⑤说法不正确.
综上:说法正确的有①③④,共3个.
故选:C.
2.解:=4,4的算术平方根是2.
故选:B.
3.解:由题意可得:x=±3.
故选:B.
4.解:A、16的平方根是±4,原说法错误,故此选项不符合题意;
B、﹣16没有平方根,原说法错误,故此选项不符合题意;
C、16的算术平方根是4,原说法错误,故此选项不符合题意;
D、16的算术平方根是4,原说法正确,故此选项符合题意.
故选:D.
5.解:A.21的平方根是,正确,故选项不符合题意;
B. 的平方根是,原说法错误.故选项符合题意;
C.0.01的算术平方根是0.1,正确,故选项不符合题意;
D.﹣5是25的一个平方根,正确,故选项不符合题意;
故选:B.
6.解:所作的正方形的面积为9×9+24×6=225(cm2),
所以所作的正方形的边长为=15(cm),
故选:A.
7.解:∵一个非0的数的平方根有两个,算术平方根有一个,
∴4的平方根是±2,
∴A选项不合题意,
∵=4,4的平方根是±2,
∴B选项不合题意,
∵25的平方根是±5,
∴C选项符合题意,
∵负数没有平方根,
∴D选项不合题意,
故选:C.
8.解:A.负数没有算术平方根,故A选项不符合题意;
B.,故B选项符合题意;
C.,故C选项不符合题意;
D.,故D选项不符合题意.
故选:B.
9.解:=9,
9的平方根为±=±3,
故选:D.
二.填空题(共12小题,满分36分)
10.解:∵=9,
∴实数的平方根是±=±3.
故答案为:±3.
11.解:根据题意得:m=(﹣)2=3,
则m+13=16,
因为16的算术平方根为4,
所以m+13的算术平方根是4.
故答案为:4.
12.解:∵平方根只有一个的数是0,
∴x﹣2=0,
∴x=2.
故答案为:2.
13.解:根据题意得:2a+1+4﹣3a=0,
解得:a=5.
故答案为:5.
14.解:∵一个数的两个平方根分别是2a+4和a+14,
∴(2a+4)+(a+14)=0,
解得a=﹣6,
a+14=﹣6+14=8,
8的平方是64.
故这个数是64.
故答案为:64.
15.解:25的算术平方根为=5,即x=5,
∵4是y+1的一个平方根,
∴y+1=16,即y=15,
∴x﹣y=5﹣15=﹣10,
故答案为:﹣10.
16.解:根据二次根式有意义的条件得:m﹣5≥0,
∴m≥5,
根据条件得:=5﹣m,
根据算术平方根的非负性得:5﹣m≥0,
∴m≤5,
∴m=5,
∴===3,
故答案为:3.
17.解:=0.09,
0.09的算术平方根是0.3.
故答案为:0.3.
18.解:设这个正方形的边长为x(x>0).
由题意得:x2=3.
∴x=.
故答案为:.
19.解:由题意得:a﹣1+3﹣2a=0.
∴a=2.
故答案为:2.
20.解:若一个数的一个平方根是,则它的另一个平方根是﹣.
故答案为:﹣.
21.解:∵32=9,
∴=3,
故答案为:9.
三.解答题(共6小题,满分57分)
22.解:(1)∵数m的两个不相等的平方根为a+2和3a﹣18,
∴(a+2)+(3a﹣18)=0,
∴4a=16,
解得a=4;
(2)∴a+2=4+2=6,3a﹣18=3×4﹣18=﹣6,
∴m=(±6)2=36,
∴m的值是36.
23.解:∵(a+3)2+,
∴a+3=0,b﹣2=0,c﹣2021=0,
解得:a=﹣3,b=2,c=2021.
∴(a+b)c=(﹣3+2)2021=﹣1.
24.(1)证明:因为=4,=10,=20,
所以2,8,50这三个数是“老根数”;
其中最小算术平方根是4,最大算术平方根是20;
(2)解:当a<16时,则2=,
解得a=9,
当16<a<36时,则2=,解得a=0,不合题意舍去;
当a>36时,则2=,
解得a=64,
综上所述,a=9或a=64.
25.解:(1)由表可得:,;
故答案为:16,16;
(2)由表可得:272.25的平方根为:;
故答案为:±16.5;
(3)∵a,b是表中两个相邻的数,a<<b,
∴a=16.7,b=16.8.
故答案为:16.7,16.8.
26.解:(1)∵x的算术平方根为3,
∴x=32=9,
即1﹣2a=9,
∴a=﹣4;
(2)根据题意得:x+y=0,
即:1﹣2a+3a﹣4=0,
∴a=3,
∴x=1﹣2a=1﹣2×3=1﹣6=﹣5,
∴这个正数为(﹣5)2=25.
27.解:(1)∵=x,=2,z是9的算术平方根,
∴x=5,y=4,z=3,
∴2x+y﹣z=2×5+4﹣3=11,
∴2x+y﹣z的平方根是±.
(2)x2=132﹣122=25(cm2),
图中阴影部分的面积是25cm2.
