第29章直线与圆的位置关系 同步达标测评 2021-2022学年冀教版九年级数学下册(word版含答案)
文档属性
| 名称 | 第29章直线与圆的位置关系 同步达标测评 2021-2022学年冀教版九年级数学下册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 367.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-13 10:14:51 | ||
图片预览


文档简介
2021-2022学年冀教版九年级数学下册《第29章直线与圆的位置关系》
同步达标测评(附答案)
一.选择题(共12小题,满分36分)
1.如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则下列各点中在⊙A外的是( )
A.点A B.点B C.点C D.点D
2.如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,﹣1),AB=.将⊙P沿着与y轴平行的方向平移多少距离时⊙P与x轴相切( )
A.1 B.2 C.3 D.1或3
3.如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,﹣4),则圆心M的坐标为( )
A.(﹣2,2.5) B.(2,﹣1.5) C.(2.5,﹣2) D.(2,﹣2.5)
4.如图,在四边形ABCD中,∠BAD=25°,∠C=90°,∠ADC=115°,O为AB的中点,以点O为圆心、AO长为半径作圆,恰好使得点D在⊙O上,连接OD,若∠EAD=25°,下列说法中不正确的是( )
A.D是劣弧的中点 B.CD是⊙O的切线
C.AE∥OD D.∠OBC=120°
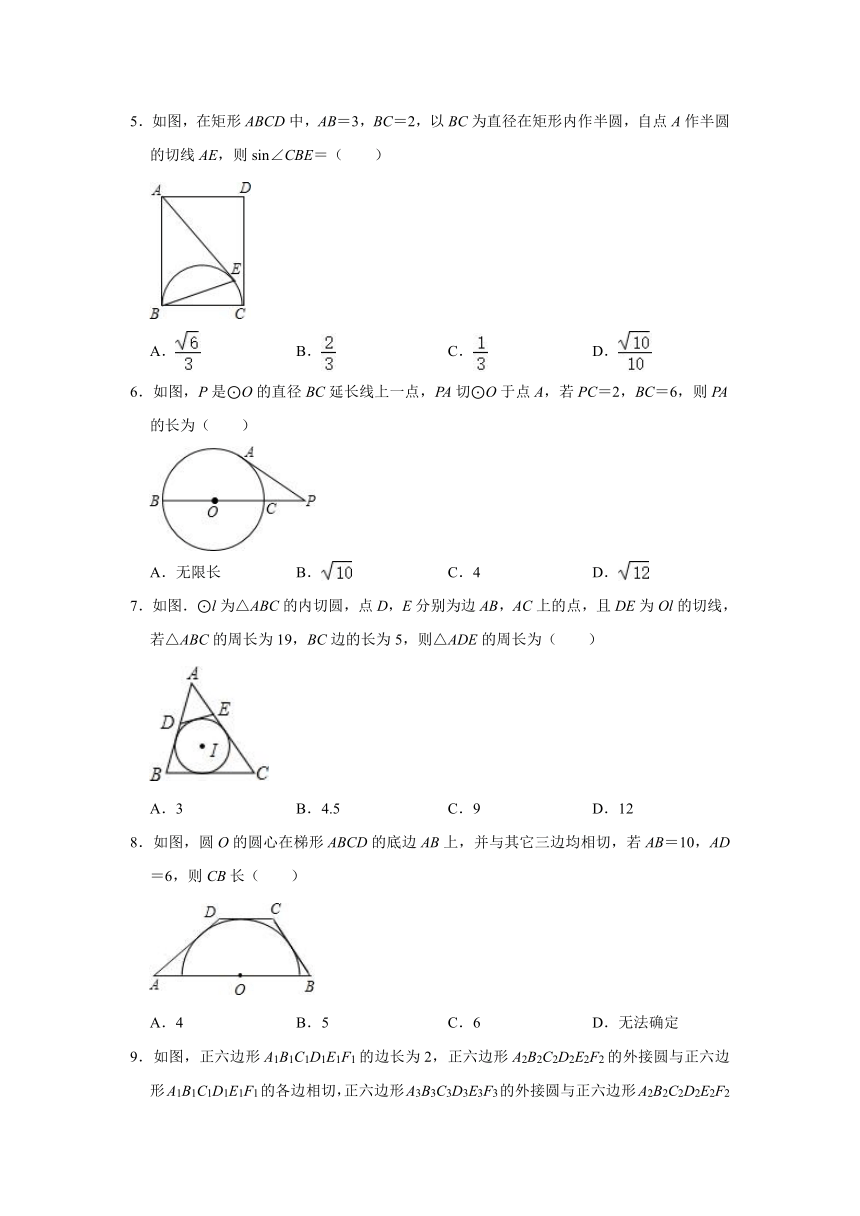
5.如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )
A. B. C. D.
6.如图,P是⊙O的直径BC延长线上一点,PA切⊙O于点A,若PC=2,BC=6,则PA的长为( )
A.无限长 B. C.4 D.
7.如图.⊙l为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为Ol的切线,若△ABC的周长为19,BC边的长为5,则△ADE的周长为( )
A.3 B.4.5 C.9 D.12
8.如图,圆O的圆心在梯形ABCD的底边AB上,并与其它三边均相切,若AB=10,AD=6,则CB长( )
A.4 B.5 C.6 D.无法确定
9.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A. B. C. D.
10.如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在直线AB上,且位于点O左侧的距离6cm处.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.4 B.8 C.4或6 D.4或8
11.如图所示,已知PA、PB切⊙O于A、B两点,C是上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56°,则∠MON=( )
A.56° B.60° C.62° D.不可求
12.如图平面上有两个全等的正十边形ABCDEFGHIJ、A′B′C′D′E′F′G′H′I′J′,其中A点与A′点重合,C点与C′点重合.求∠BAJ′的度数为何?( )
A.96 B.108 C.118 D.126
二.填空题(共6小题,满分30分)
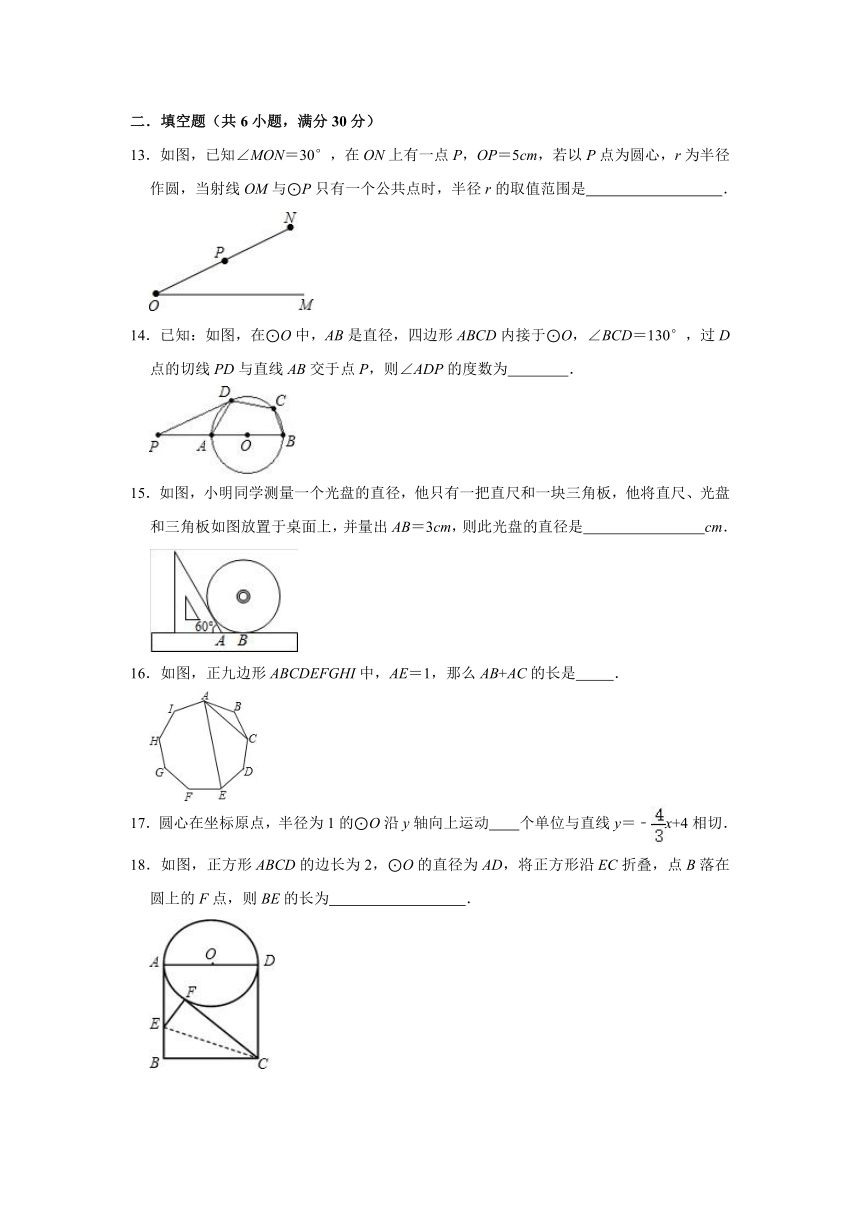
13.如图,已知∠MON=30°,在ON上有一点P,OP=5cm,若以P点为圆心,r为半径作圆,当射线OM与⊙P只有一个公共点时,半径r的取值范围是 .
14.已知:如图,在⊙O中,AB是直径,四边形ABCD内接于⊙O,∠BCD=130°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为 .
15.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是 cm.
16.如图,正九边形ABCDEFGHI中,AE=1,那么AB+AC的长是 .
17.圆心在坐标原点,半径为1的⊙O沿y轴向上运动 个单位与直线y=﹣x+4相切.
18.如图,正方形ABCD的边长为2,⊙O的直径为AD,将正方形沿EC折叠,点B落在圆上的F点,则BE的长为 .
三.解答题(共6小题,满分54分)
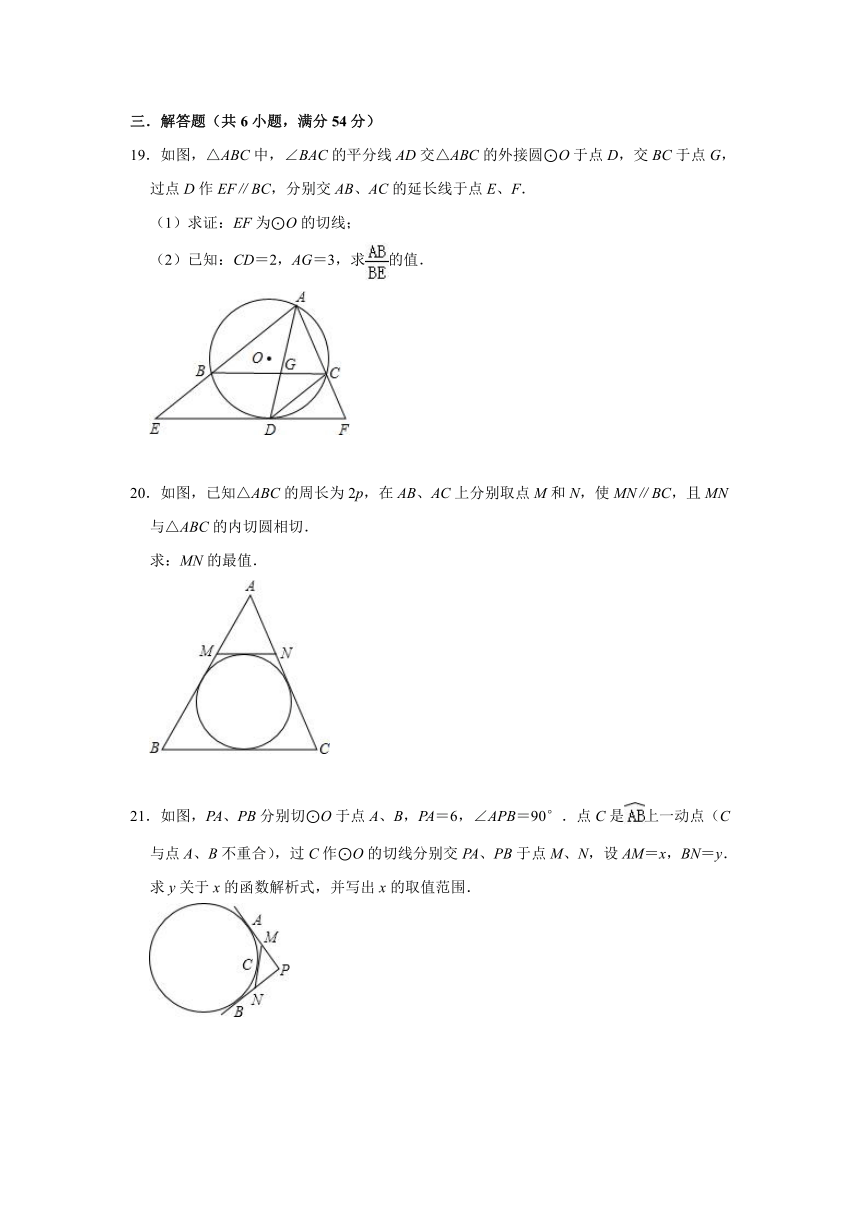
19.如图,△ABC中,∠BAC的平分线AD交△ABC的外接圆⊙O于点D,交BC于点G,过点D作EF∥BC,分别交AB、AC的延长线于点E、F.
(1)求证:EF为⊙O的切线;
(2)已知:CD=2,AG=3,求的值.
20.如图,已知△ABC的周长为2p,在AB、AC上分别取点M和N,使MN∥BC,且MN与△ABC的内切圆相切.
求:MN的最值.
21.如图,PA、PB分别切⊙O于点A、B,PA=6,∠APB=90°.点C是上一动点(C与点A、B不重合),过C作⊙O的切线分别交PA、PB于点M、N,设AM=x,BN=y.
求y关于x的函数解析式,并写出x的取值范围.
22.如图,正六边形ABCDEF的面积为54cm2,AP=2PF,CQ=2BQ.求四边形CEPQ的面积.
23.已知y是关于x的函数,且x,y满足方程组,
(1)求函数y的表达式;
(2)若点P的坐标为(m,0),求以P为圆心、1为半径的圆与函数y的图象有交点时,m的取值范围.
24.已知:如图,△ABC中,∠C=90°,AC=2cm,BC=4cm,CM是中线,以C为圆心,以cm长为半径画圆,则点A、B、M与⊙C的关系如何?
参考答案
一.选择题(共12小题,满分36分)
1.解:连接AC,
∵AB=3cm,AD=4cm,
∴AC=5cm,
∵AB=3<4,AD=4=4,AC=5>4,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外.
故选:C.
2.解:连接PA,作PC⊥AB于点C,由垂径定理得:
AC=AB=×2=,
在直角△PAC中,由勾股定理得:PA2=PC2+AC2,即PA2=12+()2=4,
∴PA=2,
∴⊙P的半径是2.
将⊙P向上平移,当⊙P与x轴相切时,平移的距离=1+2=3;
将⊙P向下平移,当⊙P与x轴相切时,平移的距离=2﹣1=1.
故选:D.
3.解:∵四边形ABCO是正方形,A(0,﹣4),
∴AB=OA=CO=BC=4,
过M作MN⊥AB于N,连接MA,
由垂径定理得:AN=AB=2,
设⊙M的半径是R,则MN=8﹣R,AM=R,由勾股定理得:AM2=MN2+AN2,
R2=(4﹣R)2+22,
解得:R=,
∵AN=2,四边形ABCO是正方形,⊙M于x轴相切,
∴M的横坐标是2,
即M(2,﹣).
故选:D.
4.解:∵∠BAD=25°,∠EAD=25°,
∴∠BAD=∠EAD,
∴,
∴D是的中点,选项A正确;
∵OA=OD,
∴∠ADO=∠BAD=25°,
∴∠ODC=∠ADC﹣∠ADO=115°﹣25°=90°,
∴CD⊥OD,
∴CD是⊙O的切线,选项B正确;
∵∠BOD=2∠BAD=50°,∠BAE=25°+25°=50°,
∴∠BOD=∠BAE,
∴AE∥OD,选项C正确;
∵∠C=90°,
∴∠OBC=360°﹣90°﹣90°﹣50°=130°≠120°,选项D不正确;
故选:D.
5.解:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F
∵AB,AE都为圆的切线
∴AE=AB
∵OB=OE,AO=AO
∴△ABO≌△AEO(SSS)
∴∠OAB=∠OAE
∴AO⊥BE
在直角△AOB里AO2=OB2+AB2
∵OB=1,AB=3
∴AO=
易证明△BOF∽△AOB
∴BO:AO=OF:OB
∴1:=OF:1
∴OF=
sin∠CBE==
故选:D.
6.解:∵PC=2,BC=6,
∴PB=8,
∵PA2=PC PB=16,
∴PA=4.
故选:C.
7.解:∵⊙l为△ABC的内切圆,
∴DM=DN,EM=EH,BN=BG,CH=CG,
∵△ABC的周长为19,BC边的长为5,
∴BG+CG=BN+CH=BC=5,AB+AC+BC=19,
∴AB+AC=19﹣BC=14,
∴△ADE的周长为:AD+DE+AE=AD+AE+DM+EM=AD+AE+DN+EH=AN+AH=AB+AC﹣BN﹣CH=(AB+AC)﹣(BN+CH)=14﹣5=9.
故选:C.
8.解:方法1、
设圆O的半径是R,圆O与AD、DC、CB相切于点E、F、H,连接OE、OD、OF、OC、OH.
设CD=y,CB=x.
设S梯形ABCD=S
则S=(CD+AB)R=(y+10)R﹣﹣﹣﹣(1)
S=S△BOC+S△COD+S△DOA
=xR+yR+×6R﹣﹣﹣﹣(2)
联立(1)(2)得x=4;
方法2、连接OD.OC
∵AD,CD是⊙O的切线,
∴∠ADO=∠ODC,
∵CD∥AB,
∴∠ODC=∠AOD,
∴∠ADO=∠AOD
∴AD=OA
∵AD=6,
∴OA=6,
∵AB=10,
∴OB=4,
同理可得
OB=BC=4,
故选:A.
9.解:连接OE1,OD1,OD2,如图,
∵六边形A1B1C1D1E1F1为正六边形,
∴∠E1OD1=60°,
∴△E1OD1为等边三角形,
∵正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,
∴OD2⊥E1D1,
∴OD2=E1D1=×2,
∴正六边形A2B2C2D2E2F2的边长=×2,
同理可得正六边形A3B3C3D3E3F3的边长=()2×2,
则正六边形A10B10C10D10E10F10的边长=()9×2=.
故选:D.
10.解:由题意CD与圆P1相切于点E,点P在射线OA上,点P只能在直线CD的左侧.∴P1E⊥CD
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2cm
又∵OP=6cm
∴P1P=4cm
∴圆P到达圆P1需要时间为:4÷1=4(秒)
∴⊙P与直线CD相切时,时间为4秒,
当点P在点O的右侧时,同法可得t=8秒
故选:D.
11.解:∠PMN+∠PNM=180°﹣∠P=124°,
∠AMN+∠BNM=360°﹣124°=236°,
∵MA、MC是⊙O的切线,
∴∠AMO=∠CMO,
∵NB、NC是⊙O的切线,
∴∠BNO=∠CNO,
∴∠CMO+∠CNO=(∠AMN+∠BNM)=118°,
∴∠MON=180°﹣118°=62°,
故选:C.
12.解题技巧:(1)正n边形每一个内角度数=,(2)菱形的邻角互补
[解析]∵两个图形为全等的正十边形,
∴ABCB′为菱形,
又∠ABC=∠AB′C==144°
∴∠BAB′=180°﹣144°=36°,
∠BAJ′=∠B′AJ′﹣∠BAB′
=144°﹣36°
=108°.
故选:B.
二.填空题(共6小题,满分30分)
13.解:①如图1,当⊙P与射线OM相切时,⊙P与射线OM只有一个公共点.
则PD⊥OM,
∵∠MON=30°,OP=5cm,
∴PD=2.5cm,
∴当⊙P的半径r满足2.5cm时,⊙P与射线OM只有一个公共点.
②如图2,当⊙P与射线OM相交时,
r>5cm,只有一个交点
综上所述,当r=2.5cm或r>5cm时,⊙P与射线OM只有一个公共点.
故答案是:r=2.5cm或r>5cm.
14.解:连接BD,则∠ADB=90°,
又∠BCD=130°,
故∠DAB=50°,
所以∠DBA=40°;
又因为PD为切线,
故∠PDA=∠ABD=40°,
即∠PDA=40°.
15.解:∵∠CAD=60°,
∴∠CAB=120°,
∵AB和AC与⊙O相切,
∴∠OAB=∠OAC,
∴∠OAB=∠CAB=60°
∵AB=3cm,
∴OA=6cm,
∴由勾股定理得OB=3cm,
∴光盘的直径6cm.
故答案为:6.
16.解:∵正九边形内角和为(9﹣2)×180°=1260°,
∴每个内角为140°,
又∵AB=AC,∠B=140°,
∴∠CAB=(180°﹣140°)÷2=20°,
连接AH,作HM,GN分别垂直AE于M,N.
∵∠CAE=2∠CAB=2×20°=40°.
∴∠HAM=140°﹣2×20°﹣40°=60°,
∴∠AHM=30°,
设AM=EN=x,MN=y,
四边形HGNM是矩形,所以HG=y,即正九边形边长为y,
在Rt△AHM中,∠AHM=∠30°,
∴AH=2AM=2x,
∴AB+AC=y+2x,
而x+y+x=1,
∴2x+y=1,
∴AB+AC=1.
故答案为:1.
17.解:如图,
令y=﹣x+4=0,解得:x=3,
令x=0,解得:y=4,
∴直线与两坐标轴的交点坐标为:A(3,0),B(0,4)
∵OD⊥AB,OC⊥AB,
∴△ODB∽△AMB,△BOC∽△BAM,
∴,
即:,或
解得:BO=或BO=,
∴OM=或,
∴半径为1的⊙O沿y轴向上运动或个单位与直线y=﹣x+4相切.
故答案为:或.
18.解:如图:连接OF,OC.
在△OCF和△OCD中,
∵OF=OD,OC=OC,CF=CD,
∴△OCF≌△OCD,
∴∠OFC=∠ODC=90°,
∴CF是⊙O的切线.
∵∠CFE=∠B=90°,
∴E,F,O三点共线.
∵EF=EB,
∴在△AEO中,AO=1,AE=2﹣BE,EO=1+BE,
∴(1+BE)2=1+(2﹣BE)2,
解得:BE=.
故答案是:.
三.解答题(共6小题,满分54分)
19.(1)证明:连接OD,
∵∠BAD=∠CAD,
∴弧BD与弧CD相等,
∴OD⊥BC,
∵EF∥BC,
∴OD⊥EF,所以,EF为⊙O的切线.
(2)解:∵∠DCG=∠BAD,∠BAD=∠DAC,
∴∠DCG=∠DAC
∵∠CDG=∠ADC,
∴△DCG∽△DAC,
∴,
设DG=x,则x(x+3)=4,取正根,得x=1,所以DG=1,
∵EF∥BC,
∴.
20.解:设BC=a,BC边上的高为h,
内切圆半径为r.
∵△AMN∽△ABC,,
MN=a(1﹣),
由S△ABC=ar+br+cr=(a+b+c)r= 2pr=rp,
∴r=,
∴MN=a(1﹣)=p (1﹣)≤p[]2=,
当且仅当=1﹣,
即a=时,取等号,
∴MN的最大值为.
21.解:∵MA=MC=x,BN=CN=y,则MN=x+y.
∴MP=6﹣x,NP=6﹣y.
在直角△MNP中,根据勾股定理可得:(6﹣x)2+(6﹣y)2=(x+y)2.
即72﹣12x﹣12y=2xy
∴y=
即y=,(0<x<6)
22.解:如图,
S△PEF=3,S△CDE=9,S四边形ABQP=11.
上述三块面积之和为3+9+11=23.
因此,四边形CEPQ面积为54﹣23=31.
23.解:(1)
,
①×3,得3x+9y=12﹣3a③,
②+③,得4x+8y=12,即x+2y=3,
得,;
(2)当y=0时,x=3,即函数y的图象与x轴交于点A(3,0),
当x=0时,y=,即函数y的图象与y轴交于点B(0,),
当圆P与直线y相切时,设切点为C,则PC⊥直线y,
此时∠PCA=90°
∴∠PCA=∠BOA,
且∠BAO=∠PAC,
∴△ABO∽△APC,
∴,即,
∴AC=2,
∴PA=
此时,P的横坐标为3﹣或3+,
∴当圆P与直线y有交点时,3﹣≤m≤3+.
24.解:根据勾股定理,有AB==2(cm);
∵CA=2cm<cm,
∴点A在⊙O内,
∵BC=4cm>cm,
∴点B在⊙C外;
由中线定理得:CM=cm
∴M点在⊙C上.
同步达标测评(附答案)
一.选择题(共12小题,满分36分)
1.如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则下列各点中在⊙A外的是( )
A.点A B.点B C.点C D.点D
2.如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,﹣1),AB=.将⊙P沿着与y轴平行的方向平移多少距离时⊙P与x轴相切( )
A.1 B.2 C.3 D.1或3
3.如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,﹣4),则圆心M的坐标为( )
A.(﹣2,2.5) B.(2,﹣1.5) C.(2.5,﹣2) D.(2,﹣2.5)
4.如图,在四边形ABCD中,∠BAD=25°,∠C=90°,∠ADC=115°,O为AB的中点,以点O为圆心、AO长为半径作圆,恰好使得点D在⊙O上,连接OD,若∠EAD=25°,下列说法中不正确的是( )
A.D是劣弧的中点 B.CD是⊙O的切线
C.AE∥OD D.∠OBC=120°
5.如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )
A. B. C. D.
6.如图,P是⊙O的直径BC延长线上一点,PA切⊙O于点A,若PC=2,BC=6,则PA的长为( )
A.无限长 B. C.4 D.
7.如图.⊙l为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为Ol的切线,若△ABC的周长为19,BC边的长为5,则△ADE的周长为( )
A.3 B.4.5 C.9 D.12
8.如图,圆O的圆心在梯形ABCD的底边AB上,并与其它三边均相切,若AB=10,AD=6,则CB长( )
A.4 B.5 C.6 D.无法确定
9.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A. B. C. D.
10.如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在直线AB上,且位于点O左侧的距离6cm处.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.4 B.8 C.4或6 D.4或8
11.如图所示,已知PA、PB切⊙O于A、B两点,C是上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56°,则∠MON=( )
A.56° B.60° C.62° D.不可求
12.如图平面上有两个全等的正十边形ABCDEFGHIJ、A′B′C′D′E′F′G′H′I′J′,其中A点与A′点重合,C点与C′点重合.求∠BAJ′的度数为何?( )
A.96 B.108 C.118 D.126
二.填空题(共6小题,满分30分)
13.如图,已知∠MON=30°,在ON上有一点P,OP=5cm,若以P点为圆心,r为半径作圆,当射线OM与⊙P只有一个公共点时,半径r的取值范围是 .
14.已知:如图,在⊙O中,AB是直径,四边形ABCD内接于⊙O,∠BCD=130°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为 .
15.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是 cm.
16.如图,正九边形ABCDEFGHI中,AE=1,那么AB+AC的长是 .
17.圆心在坐标原点,半径为1的⊙O沿y轴向上运动 个单位与直线y=﹣x+4相切.
18.如图,正方形ABCD的边长为2,⊙O的直径为AD,将正方形沿EC折叠,点B落在圆上的F点,则BE的长为 .
三.解答题(共6小题,满分54分)
19.如图,△ABC中,∠BAC的平分线AD交△ABC的外接圆⊙O于点D,交BC于点G,过点D作EF∥BC,分别交AB、AC的延长线于点E、F.
(1)求证:EF为⊙O的切线;
(2)已知:CD=2,AG=3,求的值.
20.如图,已知△ABC的周长为2p,在AB、AC上分别取点M和N,使MN∥BC,且MN与△ABC的内切圆相切.
求:MN的最值.
21.如图,PA、PB分别切⊙O于点A、B,PA=6,∠APB=90°.点C是上一动点(C与点A、B不重合),过C作⊙O的切线分别交PA、PB于点M、N,设AM=x,BN=y.
求y关于x的函数解析式,并写出x的取值范围.
22.如图,正六边形ABCDEF的面积为54cm2,AP=2PF,CQ=2BQ.求四边形CEPQ的面积.
23.已知y是关于x的函数,且x,y满足方程组,
(1)求函数y的表达式;
(2)若点P的坐标为(m,0),求以P为圆心、1为半径的圆与函数y的图象有交点时,m的取值范围.
24.已知:如图,△ABC中,∠C=90°,AC=2cm,BC=4cm,CM是中线,以C为圆心,以cm长为半径画圆,则点A、B、M与⊙C的关系如何?
参考答案
一.选择题(共12小题,满分36分)
1.解:连接AC,
∵AB=3cm,AD=4cm,
∴AC=5cm,
∵AB=3<4,AD=4=4,AC=5>4,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外.
故选:C.
2.解:连接PA,作PC⊥AB于点C,由垂径定理得:
AC=AB=×2=,
在直角△PAC中,由勾股定理得:PA2=PC2+AC2,即PA2=12+()2=4,
∴PA=2,
∴⊙P的半径是2.
将⊙P向上平移,当⊙P与x轴相切时,平移的距离=1+2=3;
将⊙P向下平移,当⊙P与x轴相切时,平移的距离=2﹣1=1.
故选:D.
3.解:∵四边形ABCO是正方形,A(0,﹣4),
∴AB=OA=CO=BC=4,
过M作MN⊥AB于N,连接MA,
由垂径定理得:AN=AB=2,
设⊙M的半径是R,则MN=8﹣R,AM=R,由勾股定理得:AM2=MN2+AN2,
R2=(4﹣R)2+22,
解得:R=,
∵AN=2,四边形ABCO是正方形,⊙M于x轴相切,
∴M的横坐标是2,
即M(2,﹣).
故选:D.
4.解:∵∠BAD=25°,∠EAD=25°,
∴∠BAD=∠EAD,
∴,
∴D是的中点,选项A正确;
∵OA=OD,
∴∠ADO=∠BAD=25°,
∴∠ODC=∠ADC﹣∠ADO=115°﹣25°=90°,
∴CD⊥OD,
∴CD是⊙O的切线,选项B正确;
∵∠BOD=2∠BAD=50°,∠BAE=25°+25°=50°,
∴∠BOD=∠BAE,
∴AE∥OD,选项C正确;
∵∠C=90°,
∴∠OBC=360°﹣90°﹣90°﹣50°=130°≠120°,选项D不正确;
故选:D.
5.解:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F
∵AB,AE都为圆的切线
∴AE=AB
∵OB=OE,AO=AO
∴△ABO≌△AEO(SSS)
∴∠OAB=∠OAE
∴AO⊥BE
在直角△AOB里AO2=OB2+AB2
∵OB=1,AB=3
∴AO=
易证明△BOF∽△AOB
∴BO:AO=OF:OB
∴1:=OF:1
∴OF=
sin∠CBE==
故选:D.
6.解:∵PC=2,BC=6,
∴PB=8,
∵PA2=PC PB=16,
∴PA=4.
故选:C.
7.解:∵⊙l为△ABC的内切圆,
∴DM=DN,EM=EH,BN=BG,CH=CG,
∵△ABC的周长为19,BC边的长为5,
∴BG+CG=BN+CH=BC=5,AB+AC+BC=19,
∴AB+AC=19﹣BC=14,
∴△ADE的周长为:AD+DE+AE=AD+AE+DM+EM=AD+AE+DN+EH=AN+AH=AB+AC﹣BN﹣CH=(AB+AC)﹣(BN+CH)=14﹣5=9.
故选:C.
8.解:方法1、
设圆O的半径是R,圆O与AD、DC、CB相切于点E、F、H,连接OE、OD、OF、OC、OH.
设CD=y,CB=x.
设S梯形ABCD=S
则S=(CD+AB)R=(y+10)R﹣﹣﹣﹣(1)
S=S△BOC+S△COD+S△DOA
=xR+yR+×6R﹣﹣﹣﹣(2)
联立(1)(2)得x=4;
方法2、连接OD.OC
∵AD,CD是⊙O的切线,
∴∠ADO=∠ODC,
∵CD∥AB,
∴∠ODC=∠AOD,
∴∠ADO=∠AOD
∴AD=OA
∵AD=6,
∴OA=6,
∵AB=10,
∴OB=4,
同理可得
OB=BC=4,
故选:A.
9.解:连接OE1,OD1,OD2,如图,
∵六边形A1B1C1D1E1F1为正六边形,
∴∠E1OD1=60°,
∴△E1OD1为等边三角形,
∵正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,
∴OD2⊥E1D1,
∴OD2=E1D1=×2,
∴正六边形A2B2C2D2E2F2的边长=×2,
同理可得正六边形A3B3C3D3E3F3的边长=()2×2,
则正六边形A10B10C10D10E10F10的边长=()9×2=.
故选:D.
10.解:由题意CD与圆P1相切于点E,点P在射线OA上,点P只能在直线CD的左侧.∴P1E⊥CD
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2cm
又∵OP=6cm
∴P1P=4cm
∴圆P到达圆P1需要时间为:4÷1=4(秒)
∴⊙P与直线CD相切时,时间为4秒,
当点P在点O的右侧时,同法可得t=8秒
故选:D.
11.解:∠PMN+∠PNM=180°﹣∠P=124°,
∠AMN+∠BNM=360°﹣124°=236°,
∵MA、MC是⊙O的切线,
∴∠AMO=∠CMO,
∵NB、NC是⊙O的切线,
∴∠BNO=∠CNO,
∴∠CMO+∠CNO=(∠AMN+∠BNM)=118°,
∴∠MON=180°﹣118°=62°,
故选:C.
12.解题技巧:(1)正n边形每一个内角度数=,(2)菱形的邻角互补
[解析]∵两个图形为全等的正十边形,
∴ABCB′为菱形,
又∠ABC=∠AB′C==144°
∴∠BAB′=180°﹣144°=36°,
∠BAJ′=∠B′AJ′﹣∠BAB′
=144°﹣36°
=108°.
故选:B.
二.填空题(共6小题,满分30分)
13.解:①如图1,当⊙P与射线OM相切时,⊙P与射线OM只有一个公共点.
则PD⊥OM,
∵∠MON=30°,OP=5cm,
∴PD=2.5cm,
∴当⊙P的半径r满足2.5cm时,⊙P与射线OM只有一个公共点.
②如图2,当⊙P与射线OM相交时,
r>5cm,只有一个交点
综上所述,当r=2.5cm或r>5cm时,⊙P与射线OM只有一个公共点.
故答案是:r=2.5cm或r>5cm.
14.解:连接BD,则∠ADB=90°,
又∠BCD=130°,
故∠DAB=50°,
所以∠DBA=40°;
又因为PD为切线,
故∠PDA=∠ABD=40°,
即∠PDA=40°.
15.解:∵∠CAD=60°,
∴∠CAB=120°,
∵AB和AC与⊙O相切,
∴∠OAB=∠OAC,
∴∠OAB=∠CAB=60°
∵AB=3cm,
∴OA=6cm,
∴由勾股定理得OB=3cm,
∴光盘的直径6cm.
故答案为:6.
16.解:∵正九边形内角和为(9﹣2)×180°=1260°,
∴每个内角为140°,
又∵AB=AC,∠B=140°,
∴∠CAB=(180°﹣140°)÷2=20°,
连接AH,作HM,GN分别垂直AE于M,N.
∵∠CAE=2∠CAB=2×20°=40°.
∴∠HAM=140°﹣2×20°﹣40°=60°,
∴∠AHM=30°,
设AM=EN=x,MN=y,
四边形HGNM是矩形,所以HG=y,即正九边形边长为y,
在Rt△AHM中,∠AHM=∠30°,
∴AH=2AM=2x,
∴AB+AC=y+2x,
而x+y+x=1,
∴2x+y=1,
∴AB+AC=1.
故答案为:1.
17.解:如图,
令y=﹣x+4=0,解得:x=3,
令x=0,解得:y=4,
∴直线与两坐标轴的交点坐标为:A(3,0),B(0,4)
∵OD⊥AB,OC⊥AB,
∴△ODB∽△AMB,△BOC∽△BAM,
∴,
即:,或
解得:BO=或BO=,
∴OM=或,
∴半径为1的⊙O沿y轴向上运动或个单位与直线y=﹣x+4相切.
故答案为:或.
18.解:如图:连接OF,OC.
在△OCF和△OCD中,
∵OF=OD,OC=OC,CF=CD,
∴△OCF≌△OCD,
∴∠OFC=∠ODC=90°,
∴CF是⊙O的切线.
∵∠CFE=∠B=90°,
∴E,F,O三点共线.
∵EF=EB,
∴在△AEO中,AO=1,AE=2﹣BE,EO=1+BE,
∴(1+BE)2=1+(2﹣BE)2,
解得:BE=.
故答案是:.
三.解答题(共6小题,满分54分)
19.(1)证明:连接OD,
∵∠BAD=∠CAD,
∴弧BD与弧CD相等,
∴OD⊥BC,
∵EF∥BC,
∴OD⊥EF,所以,EF为⊙O的切线.
(2)解:∵∠DCG=∠BAD,∠BAD=∠DAC,
∴∠DCG=∠DAC
∵∠CDG=∠ADC,
∴△DCG∽△DAC,
∴,
设DG=x,则x(x+3)=4,取正根,得x=1,所以DG=1,
∵EF∥BC,
∴.
20.解:设BC=a,BC边上的高为h,
内切圆半径为r.
∵△AMN∽△ABC,,
MN=a(1﹣),
由S△ABC=ar+br+cr=(a+b+c)r= 2pr=rp,
∴r=,
∴MN=a(1﹣)=p (1﹣)≤p[]2=,
当且仅当=1﹣,
即a=时,取等号,
∴MN的最大值为.
21.解:∵MA=MC=x,BN=CN=y,则MN=x+y.
∴MP=6﹣x,NP=6﹣y.
在直角△MNP中,根据勾股定理可得:(6﹣x)2+(6﹣y)2=(x+y)2.
即72﹣12x﹣12y=2xy
∴y=
即y=,(0<x<6)
22.解:如图,
S△PEF=3,S△CDE=9,S四边形ABQP=11.
上述三块面积之和为3+9+11=23.
因此,四边形CEPQ面积为54﹣23=31.
23.解:(1)
,
①×3,得3x+9y=12﹣3a③,
②+③,得4x+8y=12,即x+2y=3,
得,;
(2)当y=0时,x=3,即函数y的图象与x轴交于点A(3,0),
当x=0时,y=,即函数y的图象与y轴交于点B(0,),
当圆P与直线y相切时,设切点为C,则PC⊥直线y,
此时∠PCA=90°
∴∠PCA=∠BOA,
且∠BAO=∠PAC,
∴△ABO∽△APC,
∴,即,
∴AC=2,
∴PA=
此时,P的横坐标为3﹣或3+,
∴当圆P与直线y有交点时,3﹣≤m≤3+.
24.解:根据勾股定理,有AB==2(cm);
∵CA=2cm<cm,
∴点A在⊙O内,
∵BC=4cm>cm,
∴点B在⊙C外;
由中线定理得:CM=cm
∴M点在⊙C上.
