2021-2022学年北师大版七年级数学上册 第三章 整式的加减 培优训练(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学上册 第三章 整式的加减 培优训练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 291.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-13 13:02:39 | ||
图片预览




文档简介
北师大七年上第三章整式的加减培优训练
一 单选题
1. 一组按规律排列的多项式:a+b,a2-b3,a3+b5,a4-b7,…,其中第10个式子是( )
A. a10+b19 B. a10-b19 C. a10-b17 D. a10-b21
2. 一个容器装有1升水,按照如下要求把水倒出:第1次倒出 升水,第2次倒出的水量是 升的 ,第3次倒出的水量是 升的 ,第4次倒出的水量是 升的 ,…按照这种倒水的方法,倒了10次后容器内剩余的水量是( )
A. 升 B. 升 C. 升 D. 升
3. 已知31=3,32=9, 33=27, 34=81,35=243, 36=729,…,则32017的末位数字是 ( )
A. 1 B. 3 C. 7 D. 9
4. 观察下列图形,则第n个图形中三角形的个数是 ( )
A. 2n+2 B. 4n+4 C. 4n-4 D. 4n
5. .对点(x,y)的一次操作变换记为P1(x,y),定义其变换法则如下:P1(x,y)=(x+y,x-y);且规定Pn(x,y)=P1(Pn-1(x,y))(n为大于1的整数)。如P1(1,2)=(3,-1),P2(1,2)=P1(P1(1,2))=P1(3,-1)=(2,4),P3(1,2)=P1(P2(1,2))=P1(2,4)=(6,-2)。则P2011(1,-1)=( )
A. (0,21005) B. (0,-21005) C. (0,-21006) D. (0,21006)
6. 现规定正整数n的“N运算”是:①当n为奇数时,N=3n+1;②当n为偶数时,N=n× × …(n与若干个 相乘,须使N为奇数)。如:数3经过1次“N运算”的结果是10,经过2次“N运算”的结果为5,经过3次“N运算”的结果为16,经过4次“N运算”的结果为1,则数7经过2014次的“N运算”得到的结果是( )
A. 1 B. 4 C. 5 D. 16
7. 填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
A. 38 B. 52 C. 66 D. 74
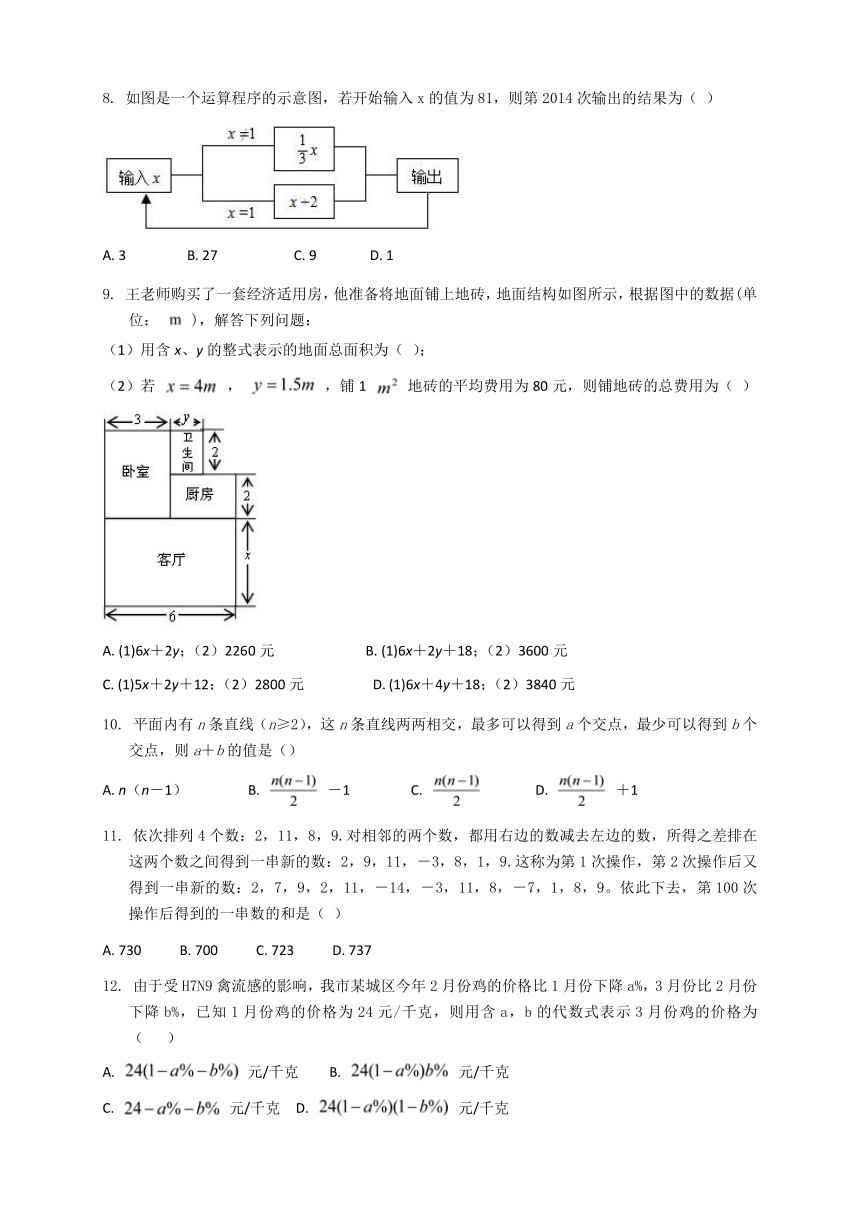
8. 如图是一个运算程序的示意图,若开始输入x的值为81,则第2014次输出的结果为( )
A. 3 B. 27 C. 9 D. 1
9. 王老师购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位: ),解答下列问题:
(1)用含x、y的整式表示的地面总面积为( );
(2)若 , ,铺1 地砖的平均费用为80元,则铺地砖的总费用为( )
A. (1)6x+2y;(2)2260元 B. (1)6x+2y+18;(2)3600元
C. (1)5x+2y+12;(2)2800元 D. (1)6x+4y+18;(2)3840元
10. 平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是()
A. n(n-1) B. -1 C. D. +1
11. 依次排列4个数:2,11,8,9.对相邻的两个数,都用右边的数减去左边的数,所得之差排在这两个数之间得到一串新的数:2,9,11,-3,8,1,9.这称为第1次操作,第2次操作后又得到一串新的数:2,7,9,2,11,-14,-3,11,8,-7,1,8,9。依此下去,第100次操作后得到的一串数的和是( )
A. 730 B. 700 C. 723 D. 737
12. 由于受H7N9禽流感的影响,我市某城区今年2月份鸡的价格比1月份下降a%,3月份比2月份下降b%,已知1月份鸡的价格为24元/千克,则用含a,b的代数式表示3月份鸡的价格为 ( )
A. 元/千克 B. 元/千克
C. 元/千克 D. 元/千克
二 填空题 13. 人民公园的侧门口有9级台阶,小聪一步只能上1级台阶或2级台阶,小聪发现当台阶数分别为1级、2级、3级、4级、5级、6级、7级……逐渐增加时,上台阶的不同方法的种数依次为1、2、3、5、8、13、21……这就是著名的斐波那契数列.那么小聪上这9级台阶共有__________________________种不同方法.
14. 将一列整式按某种规律排成x,-2x2,4x3,-8x4,16x5…则排在第六个位置的整式为__________________.
15. 代数式3x2-4x-5的值为7,则x2- x-5的值为________.
16. 已知有理数a,b满足ab<0,|a|>|b|,2(a+b)=|b﹣a|,则 的值为 _________ .
17. 如果x=1时,代数式2ax3+3bx+4的值是5,那么x=-1时,代数式2ax3+3bx+4的值是________________________________.
18. 按照如图所示的方式摆放餐桌,每个小矩形代表一张餐桌,每个小圆圈代表一个人,按这样规律下去,摆n张餐桌可以坐 __________________________ 人.
19. 正整数按下图的规律排列. 请写出第20行,第21列的数字420.
20. (2019 广东)如图1所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图2所示方法玩拼图游戏,两两相扣,相互间不留空隙,那么小明用9个这样的图形(图1)拼出来的图形的总长度是 _________________ (结果用含a,b代数式表示).
21. 已知A=2x,B是多项式,在计算B+A时,小杜同学把B+A看成了B-A,结果得x+3,则B+A=_________________________________________.
22. a是不为1的有理数,我们把 称为a的差倒数.如:2的差倒数是 =-1,-1的差倒数是 = .已知a1=- ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2015 =_________________________。
23. 若关于a,b的多项式 不含ab项,则m=________。
24. 当 , 时,代数式 的值是________________________________________。
25. 某商场-月份的销售额为a元,二月份比-月份销售额多b元,三月份比二月份减少10%,第-季度的销售额总计为________________________元;当a=2万元,b=5000元时,第-季度的总销售额为__________________________________________元.
三 解答题
26. 化简:先化简,再求值: ,其中 .
27. 先化简,再求值: ,其中 。
28. 化简求值:2[mn+(-3m)]-3(2n-mn),其中m+n=2,mn=-3.
29. 已知(a+1)2+(b-2)2+︱c-1︱=0,求:
(1)a2+ab-c的值;
(2) 的值.
30. 已知当x=-1时,代数式2mx3-3nx+6的值为17.
(1)若关于y的方程2my+n=4-ny-m的解为y=2,求mn的值;
(2)若规定[a]表示不超过a的最大整数,例如[4.3]=4,请在此规定下求[m ]的值.
31. 如果关于字母x的代数式-3x2+mx+nx2-x+10的值与x的取值无关,求m,n的值.
32. 已知代数式ax5+bx3+3x+c,当x=0时,该代数式的值为-1.
(1)求c的值;
(2)已知当x=1时,该代数式的值为-1,试求a+b+c的值;
(3)已知当x=3时,该代数式的值为9,试求当x=-3时该代数式的值;
(4)在第(3)小题的已知条件下,若有3a=5b成立,试比较a+b与c的大小.
33. 把 展开后得 ,
求 的值
34. 已知M=2x2﹣5xy+6y2,N=3y2﹣4xy+2x2,求M﹣2N,并求当x=﹣1,y=2时,M﹣2N的值.
35. 已知|b-2|+|ab-2|=0,求 的值。
36. 我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律。例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1、1,系数和为2;(a+b)2=a2+2ab+b2,它有三项,系数分别为1、2、1,系数和为4;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1、3、3、1,系数和为8;……根据以上规律,解答下列问题:
(1)(a+b)4展开式共有_________________________项,系数分别为_________________________;
(2)(a+b)n展开式共有_________________________项,系数和为_________________________。
……
37. 化简求值
(1)已知(a+2)2+︳b-3︳=0的值,求2(9ab2-1)-(7a2b+2)+2(ab2+2)-(-2a2b)的值.
(2)某位同学做一道题:已知两个多项式A、B,求A-2B的值.他误将A-2B看成2A-B,求得结果为3x2-3x+5,已知B=x2-x-1,求A-2B的正确答案.
(3)有理数a,b,c在数轴上的位置如下图所示,
若n= ,求1.5n+20的值是多少?
38. 某地电话拨号入网有两种收费方式,用户可以任选其一。(A)计时制:0.05元/分;(B)包月制:50元/月(限一部个人住宅电话上网)此外,每一种上网方式都得加收通信费0.02元/分
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用;
(2)如果某用户一个月内上网的时间为20个小时,你认为采用哪种方式较为合算?
39. 某市出租车的收费标准是:起步价10元,可乘3千米;3千米到5千米,每千米价1.3元;超过5千米,每千米价2.4元。(不足1千米的按1千米计算)
(1)若某人乘坐了2千米的路程,则他应支付的费用为__________________________元,
乘坐了4千米的路程,则他应支付的费用为__________________________元,
乘坐了8千米的路程,则他应支付的费用为__________________________元;
(2)若某人乘坐了x(x为大于5的整数)千米的路程,则他应支付的费用为__________________________元;
(3)若某人乘坐了15.4千米的路程,请聪明的你为他算一算需准备多少车费?
40. 某商场购进一批西服,进价为每套250元,原定每套以290元的价格销售,这样每天可销售200套.如果每套比原销售价降低10元销售,则每天可多销售100套.该商场为了确定销售价格,作了如下测算,请你参加测算,并由此归纳得出结论(每套西服的利润=每套西服的销售价-每套西服的进价).
(1)按原销售价销售,每天可获利润________________________元.
(2)若每套降低10元销售,每天可获利润________________________元.
(3)如果每套销售价降低10元,每天就多销售100套;每套销售价降低20元,每天就多销售200套……按这种方式,若每套降低10x元(0≤x≤4,x为正整数)列出每天所获利润的代数式:________________________.
(4)计算x=2和x=3时,该商场每天获利润多少元?
(5)根据以上的测算,如果你是该商场的经理,你将如何确定商场的销售方案.
北师大七年上第三章整式的加减培优训练参考解答
一 单选题
1. 答案:B
解析过程:多项式的第一项依次是a,a2,a3,a4,…,an,第二项依次是b,-b3,b5,-b7,…,(-1)n+1b2n-1,所以第10个式子即当n=10时,代入得到an+(-1)n+1b2n-1=a10-b19。故选B。
2. 答案:D
解析过程:思路分析:
考点解剖:考查了规律型:数字的变化,此题属于规律性题目.解答此题的关键是根据题目中的已知条件找出规律,按照此规律再进行计算即可.注意 · = ﹣ .
解题思路:根据题目中第1次倒出 升水,第2次倒出水量是 升的 ,第3次倒出水量是 升的 ,第4次倒出水量是 升的 …第10次倒出水量是 升的 …,可知按照这种倒水的方法,这1升水经10次后还有1﹣ ﹣ × ﹣ × ﹣ × … × 升水.
解答过程:
解:∵1﹣ ﹣ × ﹣ × ﹣ × …﹣ ×
=1﹣ ﹣ + ﹣ + ﹣ + …﹣ +
= .
故按此按照这种倒水的方法,这1升水经10次后还有 升水.
故选D.
规律总结:根据 对式子进行化简,然后进行计算.
3. 答案:B
解析过程:
4. 答案:D
解析过程:
5. 答案:D
解析过程:分析:根据题目提供的变化规律,找到点的坐标的变化规律并按此规律求得P2011(1,-1)的值即可.
解:P1(1,-1)=(0,2),P2(1,-1)=(2,-2)
P3(1,-1)=(0,4),P4(1,-1)=(4,-4)
P5(1,-1)=(0,8),P6(1,-1)=(8,-8)
…
当n为奇数时,Pn(1,-1)=(0, ),
∴P2011(1,-1)应该等于(0,21006).
故选D.
6. 答案:A
解析过程:n=7,第一次:3×7+1=22,第二次:22× =11,第三次:3×11+1=34,第四次:34× =17,第五次:17×3+1=52,第六次:52× × =13,第七次:13×3+1=40,第八次:40× × × =5,第九次:5×3+1=16,第十次:16× =1,第十一次:1×3+1=4,第十二次:4× =1,…,从第11次开始,4、1两个数字依次不断循环出现。(2014-10)÷2=1002,数7经过2014次的“N运算”得到的结果是1。故选A。
7. 答案:D
解析过程:思路分析:
观察每个正方形中的四个数之间的规律,可知每个放个右上角的数都是偶数:4.6.8.10…;左下角的数也是偶数:2,4,6,8…;右下角的数=左下角的数×右上角的数-左上角的数.
解答过程:
观察图形可知,第四个正方形左下角的数是8,右上角的数是10,
所以m的值是8×10-6=74.
拓展提升:
解此类题要认真观察、分析、探究数字的排列规律.
8. 答案:D
解析过程:第1次, ×81=27,第2次, ×27=9,第3次, ×9=3,第4次, ×3=1,第5次,1+2=3,第6次, ×3=1,…,依次类推,偶数次运算输出的结果是1,奇数次运算输出的结果是3,因为2014是偶数,所以第2014次输出的结果为1,故选D。
9. 答案:B
解析过程:思路分析:
①根据图形可知,房子的总面积包括卧室、卫生间、厨房及客厅的面积,因为四部分为矩形,分别找出各矩形的长和宽,根据矩形的面积公式计算即可;
②把x与y的值代入第一问中求得的总面积中,算出房子的总面积,然后根据地砖的单价即可求出铺地砖的总费用.
解答过程:
解:①设地面的总面积为S,由题意可知:S=3×(2+2)+2y+3×2+6x=6x+2y+18;
②把x=4,y=1.5代入①求得的代数式得:S=24+3+18=45(m2),
所以铺地砖的总费用为45×80=3600(元).
答:用含x、y的整式表示的地面总面积为S=6x+2y+18,铺地砖的总费用为3600元.
拓展提升:
此类问题属于列代数式及代数式求值问题,解题时注意审清题意列出符合条件的代数式,对代数式进行去括号,合并同类项,将代数式化为最简式,然后把值代入即可.
10. 答案:D
解析过程:思路分析:
n条直线两两相交需画出图形找到最多交点个数的规律,而最少可知只有1个交点才保证两两相交.
解答过程:
解:如图:2条直线相交最多有1个交点;
3条直线相交最多有1+2个交点;
4条直线相交最多有1+2+3个交点;
5条直线相交最多有1+2+3+4个交点;
6条直线相交最多有1+2+3+4+5个交点;
…
n条直线相交有1+2+3+5+…+(n-1)= 个交点.
所以a= ,而b=1,即a+b= +1.
拓展提升:
为满足两两相交,交点最多,则每条直线都和其它直线相交,此时每条直线上有n-1个交点,一共有n条直线,但任意两条直线的交点在计数时都算了两次,所以n条直线两两相交最多有 个交点.
11. 答案:A
解析过程:如下所示,开始时的和为30,第1次操作后的和为30+7,第2次操作后的和为30+7+7,…,第100次操作后的和为30+7×100=730。
12. 答案:D
二 填空题
13. 答案:55
解析过程:分析:根据斐波那契数列的特点:数列从第三项开始,每一项都等于前两项之和,可知:上第8个台阶应有13+21=34种方法,上第9个台阶应有21+34=55种方法.
解:由题意,可得:第8个台阶有13+21=34种上法,因此上这9级台阶共有21+34=55种方法.
14. 答案:-32x6
解析过程:思路分析:
考点解剖:此题考查的知识点是单项式,确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.分别找出单项式的系数和次数的规律也是解决此类问题的关键.
解题思路:符号的规律:n为奇数时,单项式为正号,n为偶数时,符号为负号;系数的绝对值的规律:第n个对应的系数的绝对值是2n-1.指数的规律:第n个对应的指数是n.
解答过程:
解:根据分析的规律,得:
第六个位置的整式为:-26x6=-32x6.
故答案为:-32x6.
规律总结:寻找结论与序号之间的统一规律,把结论用含有序号的式子表示出来是解决规律探究问题的关键.一般地,解题要关注:(1)观察式与数的特征(或图形的结论);(2)通过对简单、特殊情况的观察,再推广到一般情况.规律探究的注意点:(1)遵循类推原则,项找通项的变化规律;(2)遵循有序原则,从特殊开始,从简单开始,先连续找几个,发现规律,再验证、运用规律.
15. 答案:-1
解析过程:∵ ,
∴ ,
∴ ,
∴ .
本题采用的是整体代入法,利用等式的基本性质,把含字母的项的值化简出来,再整体代入求值.但如果没有理解题目含义,则可能出现先解 这个一元二次方程,再把求出来的解代回到代数式 中再计算求值的情况,那就非常麻烦了.
16. 答案:﹣3或
解析过程:根据ab<0得出两种情况:①当a>0,b<0时,②当a<0,b>0时,去掉绝对值符号,即可得出答案.
解:∵有理数a,b满足ab<0,
∴a>0,b<0或a<0,b>0,
①当a>0,b<0时,
∵|a|>|b|,
∴b﹣a<0,
∵2(a+b)=|b﹣a|,
∴2a+2b=a﹣b,
a=﹣3b;
=﹣3;
②当a<0,b>0时,
∵|a|>|b|,
∴b﹣a>0,
∵2(a+b)=|b﹣a|,
∴2a+2b=b﹣a,
3a=﹣b;
=
故答案为:﹣3或 .
点评:本题考查了绝对值,有理数的运算法则的应用,能求出符合的所有情况是解此题的关键.
17. 答案:3
解析过程:把x=1代入2ax3+3bx+4=5,进行变形,然后利用整体代入法求值.
因为当x=1时,代数式2ax3+3bx+4的值是5,
所以2a+3b+4=5,即2a+3b=1.
当x=-1时,2ax3+3bx+4=-2a-3b+4=-(2a+3b)+4=-1+4=3.
18. 答案:
解析过程:
19. 答案:420
解析过程:第一行第一列的数字为1,第二行第一列的数字为4=22,第三行第一列的数字为9=32,……第20行第一列的数字为202=400,则第一行第21列的数字为401,第二行第21列的数字为402……第20行第21列的数字为420.本题为规律探究题,通过数表,寻找数字间的规律并运用这一规律解决问题.
规律探究题一直是中考的热点,解决这类问题,要注意横向、纵向分别探究其规律,由特殊到一般,再由一般回到特殊.
20. 答案:a+8b
解析过程:用9个这样的图形的总长减去拼接时的重叠部分,即可得到拼出来的图形的总长度.
解:由图可得,拼出来的图形的总长度=9a﹣8(a﹣b)=a+8b.
本题主要考查了利用轴对称设计图案,利用轴对称设计图案关键是要熟悉轴对称的性质,利用轴对称的作图方法来作图,通过变换对称轴来得到不同的图案.
21. 答案:5x+3
解析过程:
22. 答案:
解析过程:∵a1=- ,
a2= ,
a3= ,
a4= ,
…
∴数列以 , ,4三个数依次不断循环,
∵2015÷3=672……2,
∴a2015=a2= .
故答案为: .
23. 答案:-6
解析过程:所谓“关于a,b的多项式”的意思是指把这个多项式中的a,b看成字母而把其他的字母看成常数,首先进行化简:
原式= ,
因为其中不含ab项,故 ,即 。
24. 答案:-252
解析过程:因为
=[ ]+[ ]+…+[ ]
=-1008b=-1008× =-252
25. 答案:(2.9a+1.9b),67500
解析过程:
三 解答题
26. 答案:
解析过程:原式=
把 代入上式,得原式
27. 答案:-1
解析过程:把 看成一个整体,利用换元法求解。
设 ,
则
因为 ,所以 ,
于是原式
28. 答案:5mn-6(m+n),-27
解析过程:思路导航:先化简整理,使其含有m+n和mn,再代入求值.
2[mn+(-3m)]-3(2n-mn)
=(2mn-6m)-(6n-3mn)
=2mn-6m-6n+3mn
=5mn-6(m+n).
当m+n=2,mn=-3时,
上式=5×(-3)-6×2=-27.
点评:化简求值是整式加减中的常见题型,解答这类问题时,注意根据题目特点,恰当选取计算方法和步骤.本题已知中给出的是m+n和mn的值,因此,在化简时应将m+n和mn分别看成一个整体.
29. 答案:(1)-2;(2)
解析过程:思路导航:只要求出a、b、c的值代入上面的式子,再按照有理数混合运算法则进行运算即可.在求a、b、c的值时,注意到绝对值非负,二次方非负,它们的和为0,只有各加数为0,故问题得到解决.
答案:因为(a+1)2≥0,(b-2)2≥0,︱c-1︱≥0,
又因为(a+1)2+(b-2)2+︱c-1︱=0,
所以a+1=0,b-2=0,c-1=0,
所以a=-1,b=2,c=1。
当a=-1,b=2,c=1时,
(1)a2+ab-c=(-1)2+(-1)×2-1=-2。
(2) = = = 。
点评:在运算中经常运用以下几个关系:a,b互为相反数 a+b=0;a,b互为倒数 ab=1;︱a︱≥0,a2≥0。
30. 答案:(1) ;(2)
解析过程:解答过程:
解:∵当 时,代数式 的值为17,
∴将 代入,得 .
整理,得 . ①
(1)∵关于y的方程 的解为y=2,
∴把y=2代入以上方程,得 .
整理,得 . ②
由①,②得
②-①,得 .
系数化为1,得 .
把 代入①,解得 .
∴原方程组的解为
此时 .
31. 答案:题意可得 ∴
解析过程:合并同类项含有x的系数为0
题意可得 ∴
32. 答案:(1)把x=0代入代数式,得到c=-1 2分
(2)把x=1代入代数式,得到a+b+3+c=-1∴a+b+c=-4
(3)把x=3代入代数式,得到35a+33b+3×3+c=9
35a+33b=1.
当x=-3时,原式=(-3)5a+(-3)3b+3×(-3)+c=-(35a+33b)-9-1
=-1-9-1=-11.
(4)由(2)题得35a+33b=-9即27a+3b=-1
又5a=3b,所以27a+5a=-1
∴
则
∴
∴a+b>c.
解析过程:
33. 答案:
解析过程:思路导航:当用一般的方法不易展开运算,采用“特殊值”法往往会取得意想不到的效果。
解:令 ,则有
令 ,则有
两式相加得:
∴ 。
点评:“特殊值”一般首先考虑 这样的数。
34. 答案:﹣8
解析过程:把M与N代入M﹣2N中,去括号合并得到最简结果,将x与y的值代入计算即可求出值.
解:∵M=2x2﹣5xy+6y2,N=3y2﹣4xy+2x2,
∴M﹣2N=2x2﹣5xy+6y2﹣6y2+8xy﹣4x2=﹣2x2+3xy,
当x=﹣1,y=2时,原式=﹣2﹣6=﹣8.
点评:此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.
35. 答案:
解析过程:由题意得,b-2=0,ab-2=0,解得a=1,b=2,所以 + = + = + + = 。
36. 答案:(1)5,1、4、6、4、1;(2)n+1,2n
解析过程:(1)根据题意知,(a+b)4展开后共有5项,各项系数分别为1、(1+3)、(3+3)、(3+1)、1,即:1、4、6、4、1;(2)(a+b)n展开后共有n+1项,当a=b=1时,(a+b)n=2n,即系数和为2n。
37. 答案:(1)-420;(2)4;(3)11
解析过程:(1)由题意知:a=-2,b=3
原式=18ab2-2-7a2b-2+2ab2+4+2a2b
=20ab2-5a2b
当a=-2,b=3时,
原式=20×(-2)×9-5×(-2)2×3
=-420
(2)由已知2A= +x2-x-1
A=2x2-2x+2
所以当A=2x2-2x+2, 时
A-2b=2x2-2x+2-2(x2-x-1)
=4
(3)n=-(a+b)+b-3+a-3c-3+3c
=-6
∴当n=-6时,
原式=1.5×(-6)+20
=11
38. 答案:(1)计时制每月收费:4.2x(元);包月制每月收费:50+1.2x(元);(2)采用包月制比较合算
解析过程:思路导航:计时制0.05元/分,所以0.05×60元/时,即3元/时,通信费0.02元/分,即1.2元/时,所以第一种收费方式实为4.2元/时,如果用户每月上网x小时,则第一种收费方式总共收费4.2x元,第二种收费方式总共收费(50+1.2x)元。
答案:(1)计时制每月收费:0.05×60x+0.02×60x=3x+1.2x=4.2x(元);
包月制每月收费:50+0.02×60x=(50+1.2x)(元)。
(2)把x=20分别代入代数式4.2x和50+1.2x,得
4.2x=4.2×20=84(元),50+1.2x=50+1.2×20=74(元)。
因为84>74,所以一个月内上网的时间为20个小时时,采用包月制比较合算。
点评:生活中一些事情由于受多个因素的制约,需要人们进行决策。为了给决策者提供科学依据,需要我们对相关信息进行整理、加工。本题就是通过计算代数式的值的大小并作出比较给我们的判断提供依据的。
39. 答案:(1)10,11.3,19.8;(2)2.4x+0.6;(3)39元
解析过程:(1)10,11.3,19.8
(2)10+1.3×(5-3)+(x-5)×2.4
=2.4x+0.6
(3)因为不足1千米的按1千米计算,所以当路程为15.4千米时,x=16
2.4x+0.6
=2.4×16+0.6
=38.4+0.6
=39
答:若某人乘坐了15.4千米的路程,他需准备39元车费。
40. 答案:(1)8000;(2)9000;(3)(40-10x)(200+100x);(4)当x=2时,该商场每天获利8000元,当x=3时,商场每天获利5000元;(5)每套降低10元销售,可使每天获利最多
解析过程:分析:依据利润=每件的获利×件数,即可解决前5问,此题(1)至(5)体现了解答此题的思维过程,每一小题都很简单,解答完前四步,就自然得出第(5)步结论.
解:根据题意得:
∵依据利润=每件的获利×件数,
∴(1)(290-250)×200=8000(元),
(2)(280-250)×(200+100)=9000(元),
(3)(40-10x)(200+100x),
(4)当x=2时,利润为(40-10×2)(200+100×2)=8000(元),
当x=3时,利润为(40-10×3)(200+100×3)=5000(元),
(5)由题意可知0≤x≤4,x为正整数,
当x=0时,上式=(40-10×0)(200+100×0)=8000(元),
当x=1时,上式=(40-10×1)(200+100×1)=9000(元),
当x=4时,上式=(40-10×4)(200+100×4)=0(元),
所以每套降低10元销售时获利最多,作为商场的经理应以每套280元的价格销售.
一 单选题
1. 一组按规律排列的多项式:a+b,a2-b3,a3+b5,a4-b7,…,其中第10个式子是( )
A. a10+b19 B. a10-b19 C. a10-b17 D. a10-b21
2. 一个容器装有1升水,按照如下要求把水倒出:第1次倒出 升水,第2次倒出的水量是 升的 ,第3次倒出的水量是 升的 ,第4次倒出的水量是 升的 ,…按照这种倒水的方法,倒了10次后容器内剩余的水量是( )
A. 升 B. 升 C. 升 D. 升
3. 已知31=3,32=9, 33=27, 34=81,35=243, 36=729,…,则32017的末位数字是 ( )
A. 1 B. 3 C. 7 D. 9
4. 观察下列图形,则第n个图形中三角形的个数是 ( )
A. 2n+2 B. 4n+4 C. 4n-4 D. 4n
5. .对点(x,y)的一次操作变换记为P1(x,y),定义其变换法则如下:P1(x,y)=(x+y,x-y);且规定Pn(x,y)=P1(Pn-1(x,y))(n为大于1的整数)。如P1(1,2)=(3,-1),P2(1,2)=P1(P1(1,2))=P1(3,-1)=(2,4),P3(1,2)=P1(P2(1,2))=P1(2,4)=(6,-2)。则P2011(1,-1)=( )
A. (0,21005) B. (0,-21005) C. (0,-21006) D. (0,21006)
6. 现规定正整数n的“N运算”是:①当n为奇数时,N=3n+1;②当n为偶数时,N=n× × …(n与若干个 相乘,须使N为奇数)。如:数3经过1次“N运算”的结果是10,经过2次“N运算”的结果为5,经过3次“N运算”的结果为16,经过4次“N运算”的结果为1,则数7经过2014次的“N运算”得到的结果是( )
A. 1 B. 4 C. 5 D. 16
7. 填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
A. 38 B. 52 C. 66 D. 74
8. 如图是一个运算程序的示意图,若开始输入x的值为81,则第2014次输出的结果为( )
A. 3 B. 27 C. 9 D. 1
9. 王老师购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位: ),解答下列问题:
(1)用含x、y的整式表示的地面总面积为( );
(2)若 , ,铺1 地砖的平均费用为80元,则铺地砖的总费用为( )
A. (1)6x+2y;(2)2260元 B. (1)6x+2y+18;(2)3600元
C. (1)5x+2y+12;(2)2800元 D. (1)6x+4y+18;(2)3840元
10. 平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是()
A. n(n-1) B. -1 C. D. +1
11. 依次排列4个数:2,11,8,9.对相邻的两个数,都用右边的数减去左边的数,所得之差排在这两个数之间得到一串新的数:2,9,11,-3,8,1,9.这称为第1次操作,第2次操作后又得到一串新的数:2,7,9,2,11,-14,-3,11,8,-7,1,8,9。依此下去,第100次操作后得到的一串数的和是( )
A. 730 B. 700 C. 723 D. 737
12. 由于受H7N9禽流感的影响,我市某城区今年2月份鸡的价格比1月份下降a%,3月份比2月份下降b%,已知1月份鸡的价格为24元/千克,则用含a,b的代数式表示3月份鸡的价格为 ( )
A. 元/千克 B. 元/千克
C. 元/千克 D. 元/千克
二 填空题 13. 人民公园的侧门口有9级台阶,小聪一步只能上1级台阶或2级台阶,小聪发现当台阶数分别为1级、2级、3级、4级、5级、6级、7级……逐渐增加时,上台阶的不同方法的种数依次为1、2、3、5、8、13、21……这就是著名的斐波那契数列.那么小聪上这9级台阶共有__________________________种不同方法.
14. 将一列整式按某种规律排成x,-2x2,4x3,-8x4,16x5…则排在第六个位置的整式为__________________.
15. 代数式3x2-4x-5的值为7,则x2- x-5的值为________.
16. 已知有理数a,b满足ab<0,|a|>|b|,2(a+b)=|b﹣a|,则 的值为 _________ .
17. 如果x=1时,代数式2ax3+3bx+4的值是5,那么x=-1时,代数式2ax3+3bx+4的值是________________________________.
18. 按照如图所示的方式摆放餐桌,每个小矩形代表一张餐桌,每个小圆圈代表一个人,按这样规律下去,摆n张餐桌可以坐 __________________________ 人.
19. 正整数按下图的规律排列. 请写出第20行,第21列的数字420.
20. (2019 广东)如图1所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图2所示方法玩拼图游戏,两两相扣,相互间不留空隙,那么小明用9个这样的图形(图1)拼出来的图形的总长度是 _________________ (结果用含a,b代数式表示).
21. 已知A=2x,B是多项式,在计算B+A时,小杜同学把B+A看成了B-A,结果得x+3,则B+A=_________________________________________.
22. a是不为1的有理数,我们把 称为a的差倒数.如:2的差倒数是 =-1,-1的差倒数是 = .已知a1=- ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2015 =_________________________。
23. 若关于a,b的多项式 不含ab项,则m=________。
24. 当 , 时,代数式 的值是________________________________________。
25. 某商场-月份的销售额为a元,二月份比-月份销售额多b元,三月份比二月份减少10%,第-季度的销售额总计为________________________元;当a=2万元,b=5000元时,第-季度的总销售额为__________________________________________元.
三 解答题
26. 化简:先化简,再求值: ,其中 .
27. 先化简,再求值: ,其中 。
28. 化简求值:2[mn+(-3m)]-3(2n-mn),其中m+n=2,mn=-3.
29. 已知(a+1)2+(b-2)2+︱c-1︱=0,求:
(1)a2+ab-c的值;
(2) 的值.
30. 已知当x=-1时,代数式2mx3-3nx+6的值为17.
(1)若关于y的方程2my+n=4-ny-m的解为y=2,求mn的值;
(2)若规定[a]表示不超过a的最大整数,例如[4.3]=4,请在此规定下求[m ]的值.
31. 如果关于字母x的代数式-3x2+mx+nx2-x+10的值与x的取值无关,求m,n的值.
32. 已知代数式ax5+bx3+3x+c,当x=0时,该代数式的值为-1.
(1)求c的值;
(2)已知当x=1时,该代数式的值为-1,试求a+b+c的值;
(3)已知当x=3时,该代数式的值为9,试求当x=-3时该代数式的值;
(4)在第(3)小题的已知条件下,若有3a=5b成立,试比较a+b与c的大小.
33. 把 展开后得 ,
求 的值
34. 已知M=2x2﹣5xy+6y2,N=3y2﹣4xy+2x2,求M﹣2N,并求当x=﹣1,y=2时,M﹣2N的值.
35. 已知|b-2|+|ab-2|=0,求 的值。
36. 我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律。例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1、1,系数和为2;(a+b)2=a2+2ab+b2,它有三项,系数分别为1、2、1,系数和为4;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1、3、3、1,系数和为8;……根据以上规律,解答下列问题:
(1)(a+b)4展开式共有_________________________项,系数分别为_________________________;
(2)(a+b)n展开式共有_________________________项,系数和为_________________________。
……
37. 化简求值
(1)已知(a+2)2+︳b-3︳=0的值,求2(9ab2-1)-(7a2b+2)+2(ab2+2)-(-2a2b)的值.
(2)某位同学做一道题:已知两个多项式A、B,求A-2B的值.他误将A-2B看成2A-B,求得结果为3x2-3x+5,已知B=x2-x-1,求A-2B的正确答案.
(3)有理数a,b,c在数轴上的位置如下图所示,
若n= ,求1.5n+20的值是多少?
38. 某地电话拨号入网有两种收费方式,用户可以任选其一。(A)计时制:0.05元/分;(B)包月制:50元/月(限一部个人住宅电话上网)此外,每一种上网方式都得加收通信费0.02元/分
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用;
(2)如果某用户一个月内上网的时间为20个小时,你认为采用哪种方式较为合算?
39. 某市出租车的收费标准是:起步价10元,可乘3千米;3千米到5千米,每千米价1.3元;超过5千米,每千米价2.4元。(不足1千米的按1千米计算)
(1)若某人乘坐了2千米的路程,则他应支付的费用为__________________________元,
乘坐了4千米的路程,则他应支付的费用为__________________________元,
乘坐了8千米的路程,则他应支付的费用为__________________________元;
(2)若某人乘坐了x(x为大于5的整数)千米的路程,则他应支付的费用为__________________________元;
(3)若某人乘坐了15.4千米的路程,请聪明的你为他算一算需准备多少车费?
40. 某商场购进一批西服,进价为每套250元,原定每套以290元的价格销售,这样每天可销售200套.如果每套比原销售价降低10元销售,则每天可多销售100套.该商场为了确定销售价格,作了如下测算,请你参加测算,并由此归纳得出结论(每套西服的利润=每套西服的销售价-每套西服的进价).
(1)按原销售价销售,每天可获利润________________________元.
(2)若每套降低10元销售,每天可获利润________________________元.
(3)如果每套销售价降低10元,每天就多销售100套;每套销售价降低20元,每天就多销售200套……按这种方式,若每套降低10x元(0≤x≤4,x为正整数)列出每天所获利润的代数式:________________________.
(4)计算x=2和x=3时,该商场每天获利润多少元?
(5)根据以上的测算,如果你是该商场的经理,你将如何确定商场的销售方案.
北师大七年上第三章整式的加减培优训练参考解答
一 单选题
1. 答案:B
解析过程:多项式的第一项依次是a,a2,a3,a4,…,an,第二项依次是b,-b3,b5,-b7,…,(-1)n+1b2n-1,所以第10个式子即当n=10时,代入得到an+(-1)n+1b2n-1=a10-b19。故选B。
2. 答案:D
解析过程:思路分析:
考点解剖:考查了规律型:数字的变化,此题属于规律性题目.解答此题的关键是根据题目中的已知条件找出规律,按照此规律再进行计算即可.注意 · = ﹣ .
解题思路:根据题目中第1次倒出 升水,第2次倒出水量是 升的 ,第3次倒出水量是 升的 ,第4次倒出水量是 升的 …第10次倒出水量是 升的 …,可知按照这种倒水的方法,这1升水经10次后还有1﹣ ﹣ × ﹣ × ﹣ × … × 升水.
解答过程:
解:∵1﹣ ﹣ × ﹣ × ﹣ × …﹣ ×
=1﹣ ﹣ + ﹣ + ﹣ + …﹣ +
= .
故按此按照这种倒水的方法,这1升水经10次后还有 升水.
故选D.
规律总结:根据 对式子进行化简,然后进行计算.
3. 答案:B
解析过程:
4. 答案:D
解析过程:
5. 答案:D
解析过程:分析:根据题目提供的变化规律,找到点的坐标的变化规律并按此规律求得P2011(1,-1)的值即可.
解:P1(1,-1)=(0,2),P2(1,-1)=(2,-2)
P3(1,-1)=(0,4),P4(1,-1)=(4,-4)
P5(1,-1)=(0,8),P6(1,-1)=(8,-8)
…
当n为奇数时,Pn(1,-1)=(0, ),
∴P2011(1,-1)应该等于(0,21006).
故选D.
6. 答案:A
解析过程:n=7,第一次:3×7+1=22,第二次:22× =11,第三次:3×11+1=34,第四次:34× =17,第五次:17×3+1=52,第六次:52× × =13,第七次:13×3+1=40,第八次:40× × × =5,第九次:5×3+1=16,第十次:16× =1,第十一次:1×3+1=4,第十二次:4× =1,…,从第11次开始,4、1两个数字依次不断循环出现。(2014-10)÷2=1002,数7经过2014次的“N运算”得到的结果是1。故选A。
7. 答案:D
解析过程:思路分析:
观察每个正方形中的四个数之间的规律,可知每个放个右上角的数都是偶数:4.6.8.10…;左下角的数也是偶数:2,4,6,8…;右下角的数=左下角的数×右上角的数-左上角的数.
解答过程:
观察图形可知,第四个正方形左下角的数是8,右上角的数是10,
所以m的值是8×10-6=74.
拓展提升:
解此类题要认真观察、分析、探究数字的排列规律.
8. 答案:D
解析过程:第1次, ×81=27,第2次, ×27=9,第3次, ×9=3,第4次, ×3=1,第5次,1+2=3,第6次, ×3=1,…,依次类推,偶数次运算输出的结果是1,奇数次运算输出的结果是3,因为2014是偶数,所以第2014次输出的结果为1,故选D。
9. 答案:B
解析过程:思路分析:
①根据图形可知,房子的总面积包括卧室、卫生间、厨房及客厅的面积,因为四部分为矩形,分别找出各矩形的长和宽,根据矩形的面积公式计算即可;
②把x与y的值代入第一问中求得的总面积中,算出房子的总面积,然后根据地砖的单价即可求出铺地砖的总费用.
解答过程:
解:①设地面的总面积为S,由题意可知:S=3×(2+2)+2y+3×2+6x=6x+2y+18;
②把x=4,y=1.5代入①求得的代数式得:S=24+3+18=45(m2),
所以铺地砖的总费用为45×80=3600(元).
答:用含x、y的整式表示的地面总面积为S=6x+2y+18,铺地砖的总费用为3600元.
拓展提升:
此类问题属于列代数式及代数式求值问题,解题时注意审清题意列出符合条件的代数式,对代数式进行去括号,合并同类项,将代数式化为最简式,然后把值代入即可.
10. 答案:D
解析过程:思路分析:
n条直线两两相交需画出图形找到最多交点个数的规律,而最少可知只有1个交点才保证两两相交.
解答过程:
解:如图:2条直线相交最多有1个交点;
3条直线相交最多有1+2个交点;
4条直线相交最多有1+2+3个交点;
5条直线相交最多有1+2+3+4个交点;
6条直线相交最多有1+2+3+4+5个交点;
…
n条直线相交有1+2+3+5+…+(n-1)= 个交点.
所以a= ,而b=1,即a+b= +1.
拓展提升:
为满足两两相交,交点最多,则每条直线都和其它直线相交,此时每条直线上有n-1个交点,一共有n条直线,但任意两条直线的交点在计数时都算了两次,所以n条直线两两相交最多有 个交点.
11. 答案:A
解析过程:如下所示,开始时的和为30,第1次操作后的和为30+7,第2次操作后的和为30+7+7,…,第100次操作后的和为30+7×100=730。
12. 答案:D
二 填空题
13. 答案:55
解析过程:分析:根据斐波那契数列的特点:数列从第三项开始,每一项都等于前两项之和,可知:上第8个台阶应有13+21=34种方法,上第9个台阶应有21+34=55种方法.
解:由题意,可得:第8个台阶有13+21=34种上法,因此上这9级台阶共有21+34=55种方法.
14. 答案:-32x6
解析过程:思路分析:
考点解剖:此题考查的知识点是单项式,确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.分别找出单项式的系数和次数的规律也是解决此类问题的关键.
解题思路:符号的规律:n为奇数时,单项式为正号,n为偶数时,符号为负号;系数的绝对值的规律:第n个对应的系数的绝对值是2n-1.指数的规律:第n个对应的指数是n.
解答过程:
解:根据分析的规律,得:
第六个位置的整式为:-26x6=-32x6.
故答案为:-32x6.
规律总结:寻找结论与序号之间的统一规律,把结论用含有序号的式子表示出来是解决规律探究问题的关键.一般地,解题要关注:(1)观察式与数的特征(或图形的结论);(2)通过对简单、特殊情况的观察,再推广到一般情况.规律探究的注意点:(1)遵循类推原则,项找通项的变化规律;(2)遵循有序原则,从特殊开始,从简单开始,先连续找几个,发现规律,再验证、运用规律.
15. 答案:-1
解析过程:∵ ,
∴ ,
∴ ,
∴ .
本题采用的是整体代入法,利用等式的基本性质,把含字母的项的值化简出来,再整体代入求值.但如果没有理解题目含义,则可能出现先解 这个一元二次方程,再把求出来的解代回到代数式 中再计算求值的情况,那就非常麻烦了.
16. 答案:﹣3或
解析过程:根据ab<0得出两种情况:①当a>0,b<0时,②当a<0,b>0时,去掉绝对值符号,即可得出答案.
解:∵有理数a,b满足ab<0,
∴a>0,b<0或a<0,b>0,
①当a>0,b<0时,
∵|a|>|b|,
∴b﹣a<0,
∵2(a+b)=|b﹣a|,
∴2a+2b=a﹣b,
a=﹣3b;
=﹣3;
②当a<0,b>0时,
∵|a|>|b|,
∴b﹣a>0,
∵2(a+b)=|b﹣a|,
∴2a+2b=b﹣a,
3a=﹣b;
=
故答案为:﹣3或 .
点评:本题考查了绝对值,有理数的运算法则的应用,能求出符合的所有情况是解此题的关键.
17. 答案:3
解析过程:把x=1代入2ax3+3bx+4=5,进行变形,然后利用整体代入法求值.
因为当x=1时,代数式2ax3+3bx+4的值是5,
所以2a+3b+4=5,即2a+3b=1.
当x=-1时,2ax3+3bx+4=-2a-3b+4=-(2a+3b)+4=-1+4=3.
18. 答案:
解析过程:
19. 答案:420
解析过程:第一行第一列的数字为1,第二行第一列的数字为4=22,第三行第一列的数字为9=32,……第20行第一列的数字为202=400,则第一行第21列的数字为401,第二行第21列的数字为402……第20行第21列的数字为420.本题为规律探究题,通过数表,寻找数字间的规律并运用这一规律解决问题.
规律探究题一直是中考的热点,解决这类问题,要注意横向、纵向分别探究其规律,由特殊到一般,再由一般回到特殊.
20. 答案:a+8b
解析过程:用9个这样的图形的总长减去拼接时的重叠部分,即可得到拼出来的图形的总长度.
解:由图可得,拼出来的图形的总长度=9a﹣8(a﹣b)=a+8b.
本题主要考查了利用轴对称设计图案,利用轴对称设计图案关键是要熟悉轴对称的性质,利用轴对称的作图方法来作图,通过变换对称轴来得到不同的图案.
21. 答案:5x+3
解析过程:
22. 答案:
解析过程:∵a1=- ,
a2= ,
a3= ,
a4= ,
…
∴数列以 , ,4三个数依次不断循环,
∵2015÷3=672……2,
∴a2015=a2= .
故答案为: .
23. 答案:-6
解析过程:所谓“关于a,b的多项式”的意思是指把这个多项式中的a,b看成字母而把其他的字母看成常数,首先进行化简:
原式= ,
因为其中不含ab项,故 ,即 。
24. 答案:-252
解析过程:因为
=[ ]+[ ]+…+[ ]
=-1008b=-1008× =-252
25. 答案:(2.9a+1.9b),67500
解析过程:
三 解答题
26. 答案:
解析过程:原式=
把 代入上式,得原式
27. 答案:-1
解析过程:把 看成一个整体,利用换元法求解。
设 ,
则
因为 ,所以 ,
于是原式
28. 答案:5mn-6(m+n),-27
解析过程:思路导航:先化简整理,使其含有m+n和mn,再代入求值.
2[mn+(-3m)]-3(2n-mn)
=(2mn-6m)-(6n-3mn)
=2mn-6m-6n+3mn
=5mn-6(m+n).
当m+n=2,mn=-3时,
上式=5×(-3)-6×2=-27.
点评:化简求值是整式加减中的常见题型,解答这类问题时,注意根据题目特点,恰当选取计算方法和步骤.本题已知中给出的是m+n和mn的值,因此,在化简时应将m+n和mn分别看成一个整体.
29. 答案:(1)-2;(2)
解析过程:思路导航:只要求出a、b、c的值代入上面的式子,再按照有理数混合运算法则进行运算即可.在求a、b、c的值时,注意到绝对值非负,二次方非负,它们的和为0,只有各加数为0,故问题得到解决.
答案:因为(a+1)2≥0,(b-2)2≥0,︱c-1︱≥0,
又因为(a+1)2+(b-2)2+︱c-1︱=0,
所以a+1=0,b-2=0,c-1=0,
所以a=-1,b=2,c=1。
当a=-1,b=2,c=1时,
(1)a2+ab-c=(-1)2+(-1)×2-1=-2。
(2) = = = 。
点评:在运算中经常运用以下几个关系:a,b互为相反数 a+b=0;a,b互为倒数 ab=1;︱a︱≥0,a2≥0。
30. 答案:(1) ;(2)
解析过程:解答过程:
解:∵当 时,代数式 的值为17,
∴将 代入,得 .
整理,得 . ①
(1)∵关于y的方程 的解为y=2,
∴把y=2代入以上方程,得 .
整理,得 . ②
由①,②得
②-①,得 .
系数化为1,得 .
把 代入①,解得 .
∴原方程组的解为
此时 .
31. 答案:题意可得 ∴
解析过程:合并同类项含有x的系数为0
题意可得 ∴
32. 答案:(1)把x=0代入代数式,得到c=-1 2分
(2)把x=1代入代数式,得到a+b+3+c=-1∴a+b+c=-4
(3)把x=3代入代数式,得到35a+33b+3×3+c=9
35a+33b=1.
当x=-3时,原式=(-3)5a+(-3)3b+3×(-3)+c=-(35a+33b)-9-1
=-1-9-1=-11.
(4)由(2)题得35a+33b=-9即27a+3b=-1
又5a=3b,所以27a+5a=-1
∴
则
∴
∴a+b>c.
解析过程:
33. 答案:
解析过程:思路导航:当用一般的方法不易展开运算,采用“特殊值”法往往会取得意想不到的效果。
解:令 ,则有
令 ,则有
两式相加得:
∴ 。
点评:“特殊值”一般首先考虑 这样的数。
34. 答案:﹣8
解析过程:把M与N代入M﹣2N中,去括号合并得到最简结果,将x与y的值代入计算即可求出值.
解:∵M=2x2﹣5xy+6y2,N=3y2﹣4xy+2x2,
∴M﹣2N=2x2﹣5xy+6y2﹣6y2+8xy﹣4x2=﹣2x2+3xy,
当x=﹣1,y=2时,原式=﹣2﹣6=﹣8.
点评:此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.
35. 答案:
解析过程:由题意得,b-2=0,ab-2=0,解得a=1,b=2,所以 + = + = + + = 。
36. 答案:(1)5,1、4、6、4、1;(2)n+1,2n
解析过程:(1)根据题意知,(a+b)4展开后共有5项,各项系数分别为1、(1+3)、(3+3)、(3+1)、1,即:1、4、6、4、1;(2)(a+b)n展开后共有n+1项,当a=b=1时,(a+b)n=2n,即系数和为2n。
37. 答案:(1)-420;(2)4;(3)11
解析过程:(1)由题意知:a=-2,b=3
原式=18ab2-2-7a2b-2+2ab2+4+2a2b
=20ab2-5a2b
当a=-2,b=3时,
原式=20×(-2)×9-5×(-2)2×3
=-420
(2)由已知2A= +x2-x-1
A=2x2-2x+2
所以当A=2x2-2x+2, 时
A-2b=2x2-2x+2-2(x2-x-1)
=4
(3)n=-(a+b)+b-3+a-3c-3+3c
=-6
∴当n=-6时,
原式=1.5×(-6)+20
=11
38. 答案:(1)计时制每月收费:4.2x(元);包月制每月收费:50+1.2x(元);(2)采用包月制比较合算
解析过程:思路导航:计时制0.05元/分,所以0.05×60元/时,即3元/时,通信费0.02元/分,即1.2元/时,所以第一种收费方式实为4.2元/时,如果用户每月上网x小时,则第一种收费方式总共收费4.2x元,第二种收费方式总共收费(50+1.2x)元。
答案:(1)计时制每月收费:0.05×60x+0.02×60x=3x+1.2x=4.2x(元);
包月制每月收费:50+0.02×60x=(50+1.2x)(元)。
(2)把x=20分别代入代数式4.2x和50+1.2x,得
4.2x=4.2×20=84(元),50+1.2x=50+1.2×20=74(元)。
因为84>74,所以一个月内上网的时间为20个小时时,采用包月制比较合算。
点评:生活中一些事情由于受多个因素的制约,需要人们进行决策。为了给决策者提供科学依据,需要我们对相关信息进行整理、加工。本题就是通过计算代数式的值的大小并作出比较给我们的判断提供依据的。
39. 答案:(1)10,11.3,19.8;(2)2.4x+0.6;(3)39元
解析过程:(1)10,11.3,19.8
(2)10+1.3×(5-3)+(x-5)×2.4
=2.4x+0.6
(3)因为不足1千米的按1千米计算,所以当路程为15.4千米时,x=16
2.4x+0.6
=2.4×16+0.6
=38.4+0.6
=39
答:若某人乘坐了15.4千米的路程,他需准备39元车费。
40. 答案:(1)8000;(2)9000;(3)(40-10x)(200+100x);(4)当x=2时,该商场每天获利8000元,当x=3时,商场每天获利5000元;(5)每套降低10元销售,可使每天获利最多
解析过程:分析:依据利润=每件的获利×件数,即可解决前5问,此题(1)至(5)体现了解答此题的思维过程,每一小题都很简单,解答完前四步,就自然得出第(5)步结论.
解:根据题意得:
∵依据利润=每件的获利×件数,
∴(1)(290-250)×200=8000(元),
(2)(280-250)×(200+100)=9000(元),
(3)(40-10x)(200+100x),
(4)当x=2时,利润为(40-10×2)(200+100×2)=8000(元),
当x=3时,利润为(40-10×3)(200+100×3)=5000(元),
(5)由题意可知0≤x≤4,x为正整数,
当x=0时,上式=(40-10×0)(200+100×0)=8000(元),
当x=1时,上式=(40-10×1)(200+100×1)=9000(元),
当x=4时,上式=(40-10×4)(200+100×4)=0(元),
所以每套降低10元销售时获利最多,作为商场的经理应以每套280元的价格销售.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
