江西省赣州市十六县(市)十七校2021-2022学年高二上学期期中联考数学(理)试题(Word版含答案)
文档属性
| 名称 | 江西省赣州市十六县(市)十七校2021-2022学年高二上学期期中联考数学(理)试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 660.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 14:32:37 | ||
图片预览



文档简介
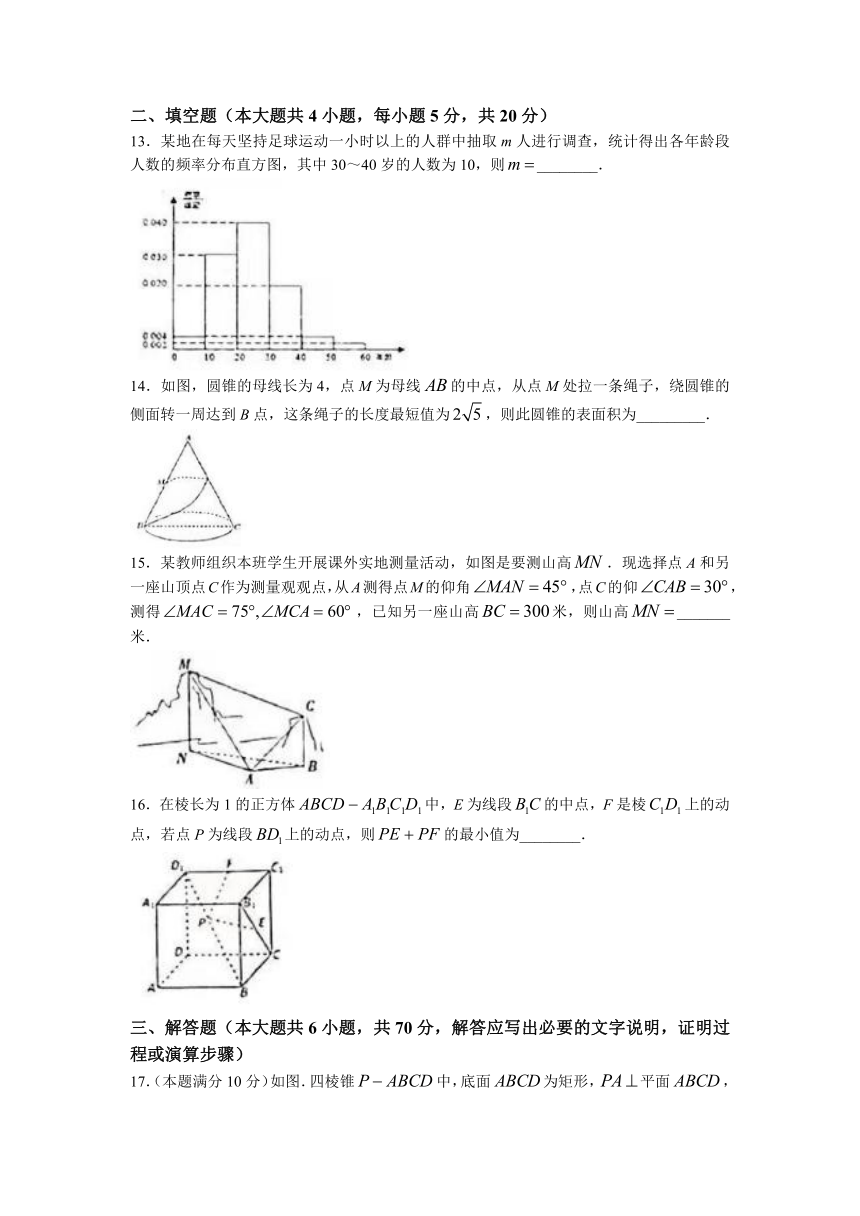
2021-2022学年第一学期州市十六县(市)十七校期中联考
高二数学(理科)试题
考试时间:120分钟 试卷满分:150分
第Ⅰ卷(选择题共60分)
一、选择题(本大题共12小题,每小题5分,共60分)
1.过点且垂直于的直线方程为( )
A. B. C. D.
2.某校高二年级为选拔参加数学竞赛的学生组织了一次考试,最后选出13名男生和7名女生,这20名学生的考试成绩如茎叶图所示(单位:分),学校规定:成绩不低于130分的人到A班培训,低于130分的人到B班培训,如果用分层抽样的方法从到A班的人和到B班的人中共选取5人,则5人中A班的有( )
A.1人 B.2人 C.3人 D.4人
3.多面体的三视图如图,它们都是斜边长为的等腰直角三角形,则多面体最长的棱长为( )
A. B. C. D.
4.如图,长方体的棱和的中点分别为E,F,,则异面直线与所成角的正切值为( )
A. B. C. D.
5.设向量.若,则与的夹角为( )
A. B. C. D.
6.设是空间中的一个平面,l,m,n是三条不同的直线,则( )
A.若,,,,则 B.若,则
C.若,则 D.若,则
7.一组数据中的第一个数据都乘以2,再减去80,得到一组新数所,若求得新的数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( )
A.40.6,1.1 B.48.8,4.4 C.81.2,44.4 D.78.8,75.6
8.如图所示,若该程序输出结果为,则判断框内应填入的条件是( )
A. B. C. D.
9.已知直线和圆,则直线l被圆C截得的弦长的最小值为( )
A.10 B.5 C. D.
10.在的条件下,目标函数的最大值为10,则的最小值是( )
A. B. C. D.
11.在三棱锥中,若该三棱锥的体积为,则三棱锥外球的体积为( )
A. B. C. D.
12.在正方体中,点P在线段上运动,则下列判断正确的个数是( )
①三棱锥的体积不变;②平面;
③平面平面;④与所成角的范围是.
A.4个 B.3个 C.2个 D.1个
第Ⅱ卷(非选择题共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13.某地在每天坚持足球运动一小时以上的人群中抽取m人进行调查,统计得出各年龄段人数的频率分布直方图,其中30~40岁的人数为10,则________.
14.如图,圆锥的母线长为4,点M为母线的中点,从点M处拉一条绳子,绕圆锥的侧面转一周达到B点,这条绳子的长度最短值为,则此圆锥的表面积为_________.
15.某教师组织本班学生开展课外实地测量活动,如图是要测山高.现选择点A和另一座山顶点C作为测量观观点,从A测得点M的仰角,点C的仰,测得,已知另一座山高米,则山高_______米.
16.在棱长为1的正方体中,E为线段的中点,F是棱上的动点,若点P为线段上的动点,则的最小值为________.
三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明,证明过程或演算步骤)
17.(本题满分10分)如图.四棱锥中,底面为矩形,平面,设E为的中点.
(1)证明:平面:
(2)设异面直线与所成角为,,求三棱锥的体积.
18.(本题满分12分)某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数x(份)与收入y(元)之间有如下的对应数据:
外卖分数x(份) 2 4 5 6 8
收入y(元) 30 40 60 50 70
(1)画出散点图;
(2)请根据以上数据用最小二乘法原理求出收入y关于份数x的线性回归方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考方式:线性回归方程系数公式;②参考数据:.
19.(本题满分1分)已知平面向量,函数.
(1)求的单调增区间:
(2)在锐角中,a,b,c分别是内角A,B,C所对的边,若,求周长的取值范围.
20.(本题满分12分)各项均为正数的数列满,且是的等差中项.
(1)求数列的通项公式;
(2)若且,求使成立的正整数n的最小值.
21.(本题满分12分)如图,三棱柱中,侧面为菱形,的中点为O,且平面.
(1)证明:;
(2)若,求二面角的余弦值.
22.(本题满分12分)已知圆C经过两点,圆心在直线上.
(1)求圆C的标准方程;
(2)若圆C与y轴相交于A,B两点(A在B上方).直线与圆C交于M,N两点,直线,相交于点T.请问点T是否在定直线上?若是,求出该直线方程;若不是,说明理由.
2021-2022学年第一学期赣州市十六县(市)十七校期中联考
高二数学(理科)参考答案
1.C 2.B 3.B 4.A 5.D 6.B 7.A 8.C 9.C 10.D 11.D 12.B
13.50 14. 15. 16.
16.作出E关于直线的对称点,过作的垂线,交于P,交与F,过作,交于G,连接.画出图像如下图所示,由于,故为最短的距离.在三角形中,设,则,而,
故,
所以,
所以.
17.(1)连接交于F,F为中点,连接. 1分
在三角形中,E为的中点,∴, 2分
∵平面平面,∴平面. 5分
(2)∵,∴异面直线与所成角的角为, 6分
∴. 7分
∴ 10分
18.(1)作出散点图如下图所示: 2分
(2), 4分
已知.由公式,
可求, 8分
因此线性回归方程为. 9分
(3)时,, 11分
即外卖份数为12份时,收入大约为95.5元. 12分
19.(1) 1分
, 3分
令,得:,
∴的单调递增区间为:; 5分
(2)由(1)可得,,那么,可得:, 6分
∵,根据正弦定理,可得, 7分
那么的周长
, 9分
∵是锐角三角形,∴,则, 10分
则, 11分
那么周长, 12分
20.(1), 1分
因为数列各项均为正数,故,所以是以公比为2的等比数列, 2分
又是的等差中项,故 ,3分
即, 4分
故. 5分
(2), 6分
故…①,所以…②,②-①得 7分
, 10分
要,即,故使成立的正整数n的最小值为5. 12分
21.(1)连接∵四边形为菱形,∴,且,∵平面平面,∴ 2分
∵与平面,∴平面, 4分
∵平面,∴. 5分
(2)作,垂足为D,连接,∵四边形为菱形,,∴为等边三角形 又,∴,∴∵平面平面,∴又平面,∴平面, 8分
∵平面,∴,∴二面角的平面角为, 10分
∵,O为中点,∴,
∴,∴,
∴二面角的余弦值为 12分
22.依题意可设圆心,
则,解, 2分
故,圆C的半径,圆C的标准方程为. 4分
(2)设,由(1)可知,, 5分
联立方程组,消去x并化简得, 6分
所以, 7分
直线的方程为,①直线的方程为,② 8分
由①②知 11分
由,化简得,故点T在定直线上. 12分
高二数学(理科)试题
考试时间:120分钟 试卷满分:150分
第Ⅰ卷(选择题共60分)
一、选择题(本大题共12小题,每小题5分,共60分)
1.过点且垂直于的直线方程为( )
A. B. C. D.
2.某校高二年级为选拔参加数学竞赛的学生组织了一次考试,最后选出13名男生和7名女生,这20名学生的考试成绩如茎叶图所示(单位:分),学校规定:成绩不低于130分的人到A班培训,低于130分的人到B班培训,如果用分层抽样的方法从到A班的人和到B班的人中共选取5人,则5人中A班的有( )
A.1人 B.2人 C.3人 D.4人
3.多面体的三视图如图,它们都是斜边长为的等腰直角三角形,则多面体最长的棱长为( )
A. B. C. D.
4.如图,长方体的棱和的中点分别为E,F,,则异面直线与所成角的正切值为( )
A. B. C. D.
5.设向量.若,则与的夹角为( )
A. B. C. D.
6.设是空间中的一个平面,l,m,n是三条不同的直线,则( )
A.若,,,,则 B.若,则
C.若,则 D.若,则
7.一组数据中的第一个数据都乘以2,再减去80,得到一组新数所,若求得新的数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( )
A.40.6,1.1 B.48.8,4.4 C.81.2,44.4 D.78.8,75.6
8.如图所示,若该程序输出结果为,则判断框内应填入的条件是( )
A. B. C. D.
9.已知直线和圆,则直线l被圆C截得的弦长的最小值为( )
A.10 B.5 C. D.
10.在的条件下,目标函数的最大值为10,则的最小值是( )
A. B. C. D.
11.在三棱锥中,若该三棱锥的体积为,则三棱锥外球的体积为( )
A. B. C. D.
12.在正方体中,点P在线段上运动,则下列判断正确的个数是( )
①三棱锥的体积不变;②平面;
③平面平面;④与所成角的范围是.
A.4个 B.3个 C.2个 D.1个
第Ⅱ卷(非选择题共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13.某地在每天坚持足球运动一小时以上的人群中抽取m人进行调查,统计得出各年龄段人数的频率分布直方图,其中30~40岁的人数为10,则________.
14.如图,圆锥的母线长为4,点M为母线的中点,从点M处拉一条绳子,绕圆锥的侧面转一周达到B点,这条绳子的长度最短值为,则此圆锥的表面积为_________.
15.某教师组织本班学生开展课外实地测量活动,如图是要测山高.现选择点A和另一座山顶点C作为测量观观点,从A测得点M的仰角,点C的仰,测得,已知另一座山高米,则山高_______米.
16.在棱长为1的正方体中,E为线段的中点,F是棱上的动点,若点P为线段上的动点,则的最小值为________.
三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明,证明过程或演算步骤)
17.(本题满分10分)如图.四棱锥中,底面为矩形,平面,设E为的中点.
(1)证明:平面:
(2)设异面直线与所成角为,,求三棱锥的体积.
18.(本题满分12分)某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数x(份)与收入y(元)之间有如下的对应数据:
外卖分数x(份) 2 4 5 6 8
收入y(元) 30 40 60 50 70
(1)画出散点图;
(2)请根据以上数据用最小二乘法原理求出收入y关于份数x的线性回归方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考方式:线性回归方程系数公式;②参考数据:.
19.(本题满分1分)已知平面向量,函数.
(1)求的单调增区间:
(2)在锐角中,a,b,c分别是内角A,B,C所对的边,若,求周长的取值范围.
20.(本题满分12分)各项均为正数的数列满,且是的等差中项.
(1)求数列的通项公式;
(2)若且,求使成立的正整数n的最小值.
21.(本题满分12分)如图,三棱柱中,侧面为菱形,的中点为O,且平面.
(1)证明:;
(2)若,求二面角的余弦值.
22.(本题满分12分)已知圆C经过两点,圆心在直线上.
(1)求圆C的标准方程;
(2)若圆C与y轴相交于A,B两点(A在B上方).直线与圆C交于M,N两点,直线,相交于点T.请问点T是否在定直线上?若是,求出该直线方程;若不是,说明理由.
2021-2022学年第一学期赣州市十六县(市)十七校期中联考
高二数学(理科)参考答案
1.C 2.B 3.B 4.A 5.D 6.B 7.A 8.C 9.C 10.D 11.D 12.B
13.50 14. 15. 16.
16.作出E关于直线的对称点,过作的垂线,交于P,交与F,过作,交于G,连接.画出图像如下图所示,由于,故为最短的距离.在三角形中,设,则,而,
故,
所以,
所以.
17.(1)连接交于F,F为中点,连接. 1分
在三角形中,E为的中点,∴, 2分
∵平面平面,∴平面. 5分
(2)∵,∴异面直线与所成角的角为, 6分
∴. 7分
∴ 10分
18.(1)作出散点图如下图所示: 2分
(2), 4分
已知.由公式,
可求, 8分
因此线性回归方程为. 9分
(3)时,, 11分
即外卖份数为12份时,收入大约为95.5元. 12分
19.(1) 1分
, 3分
令,得:,
∴的单调递增区间为:; 5分
(2)由(1)可得,,那么,可得:, 6分
∵,根据正弦定理,可得, 7分
那么的周长
, 9分
∵是锐角三角形,∴,则, 10分
则, 11分
那么周长, 12分
20.(1), 1分
因为数列各项均为正数,故,所以是以公比为2的等比数列, 2分
又是的等差中项,故 ,3分
即, 4分
故. 5分
(2), 6分
故…①,所以…②,②-①得 7分
, 10分
要,即,故使成立的正整数n的最小值为5. 12分
21.(1)连接∵四边形为菱形,∴,且,∵平面平面,∴ 2分
∵与平面,∴平面, 4分
∵平面,∴. 5分
(2)作,垂足为D,连接,∵四边形为菱形,,∴为等边三角形 又,∴,∴∵平面平面,∴又平面,∴平面, 8分
∵平面,∴,∴二面角的平面角为, 10分
∵,O为中点,∴,
∴,∴,
∴二面角的余弦值为 12分
22.依题意可设圆心,
则,解, 2分
故,圆C的半径,圆C的标准方程为. 4分
(2)设,由(1)可知,, 5分
联立方程组,消去x并化简得, 6分
所以, 7分
直线的方程为,①直线的方程为,② 8分
由①②知 11分
由,化简得,故点T在定直线上. 12分
同课章节目录
