2021—2022学年华东师大版数学九年级下册 27.2.2直线与圆的位置关系(共23张)
文档属性
| 名称 | 2021—2022学年华东师大版数学九年级下册 27.2.2直线与圆的位置关系(共23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-13 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
直
线
与
圆
的位置关系
初中数学华东师范大学出版社九年级下册
27.2
复
习
提
问
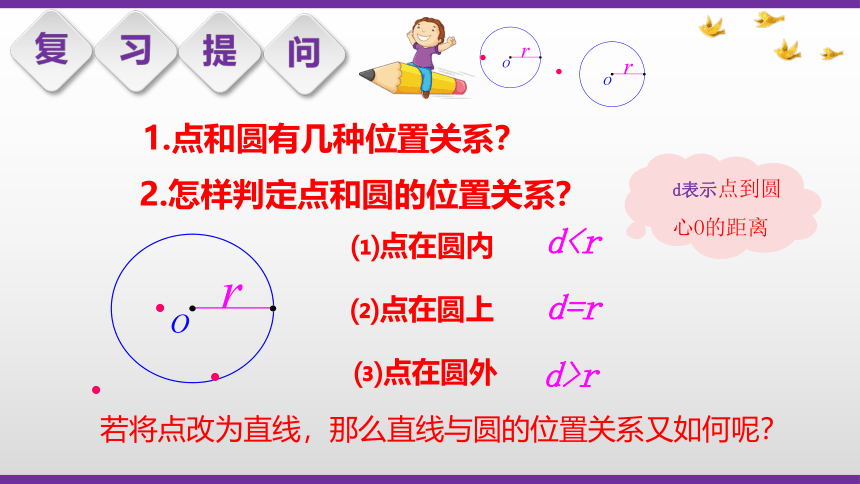
2.怎样判定点和圆的位置关系?
1.点和圆有几种位置关系?
⑴点在圆内
⑵点在圆上
⑶点在圆外
dd=r
d>r
·
·
·
·
·
d表示点到圆心O的距离
若将点改为直线,那么直线与圆的位置关系又如何呢?
一.
情 景 引 入
探 索 新 知
观察与思考
在太阳升起过程中,太阳和海平面会有那些的位置关系?
1、如果我们把太阳看作一个圆,海平面看作一条直线,请同学们利用手中的工具再现太阳升起的整个过程。(在纸上画一个圆,把你手中的笔看作一条直线,在纸上移动笔)
探究思考
3、你分类的依据是什么?
2、再现过程中,你认为直线与圆的位置关系可以分为哪几类?请在白纸上画出图形。
探 索 新 知
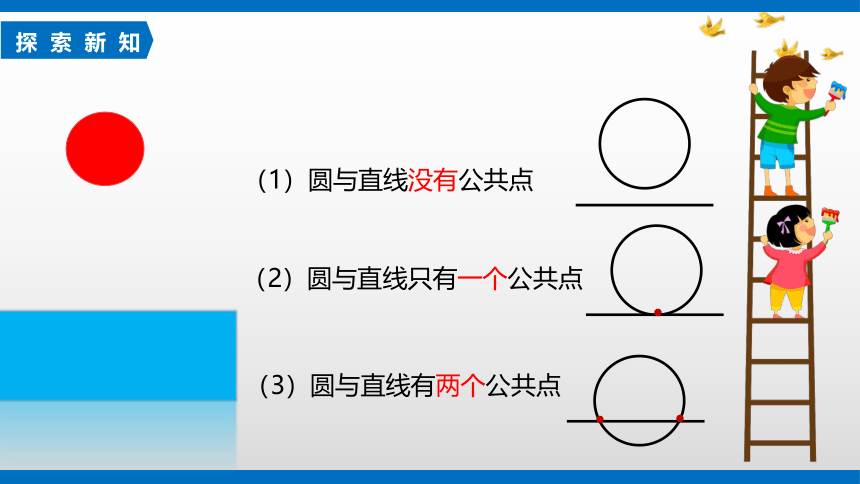
(3)圆与直线有两个公共点
·
·
(2)圆与直线只有一个公共点
·
(1)圆与直线没有公共点
探 索 新 知
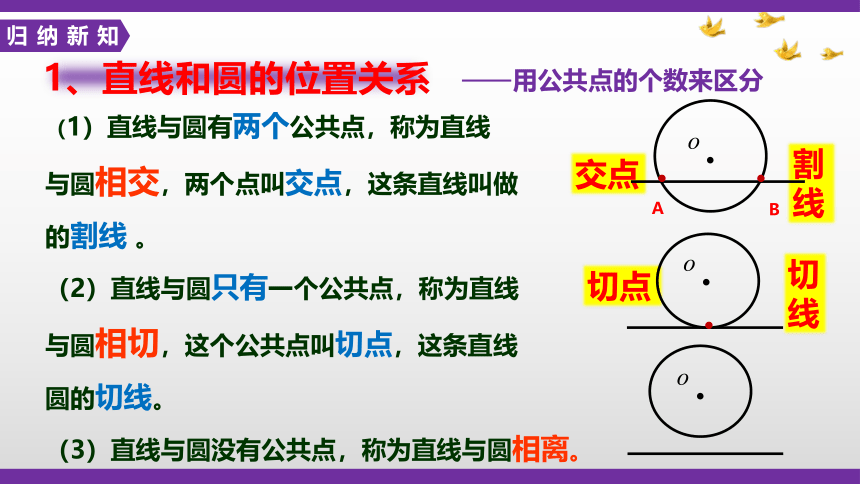
1、直线和圆的位置关系
用公共点的个数来区分
(1)直线与圆有两个公共点,称为直线
与圆相交,两个点叫交点,这条直线叫做
的割线 。
(2)直线与圆只有一个公共点,称为直线
与圆相切,这个公共点叫切点,这条直线
圆的切线。
(3)直线与圆没有公共点,称为直线与圆相离。
交点
割线
切
线
切点
A
B
·
·
·o
·
·o
·o
归纳新知
请列举出生活中有关直线和圆的位置关系的实例。
生活实例
新知巩固
练一练
下列说法是否正确,不正确的请改正。
① 若C为⊙O内一点, 则直线CO与⊙O相交。( )
② 直线和圆有一个公共点,直线与圆相切。 ( )
③ 直线与圆最多有两个公共点。( )
④ 若A、B是⊙O外两点, 则直线AB与⊙O相离。( )
√
√
×
√
新知巩固
我指你答
·o
·o
·o
·o
·o
探索新知
除了用公共点的个数来区分直线与圆的位置关系外,能否像点和圆的位置关系一样,用数量关系的方法来判断直线与圆的位置关系?
思考
?
小 组 合 作 探 究
2、直线和圆的位置关系
数量特征
:圆心到直线的距离 :圆的半径
·o
·o
·o
·o
相 交
相 切
相 离
d < r
d = r
d > r
由圆心到直线的距离d和圆半径r间的数量关系可以判定直线与圆的位置关系,反过来
思考:由直线与圆的位置关系可以得到d与r间的数量关系吗?
动画观察
2、直线和圆的位置关系
数量特征
思考:由直线与圆的位置关系可以得到d与r间的数量关系吗?
画一画
依据题目条件画出直线 ,并回答相关问题:
如图,⊙O的半径为2cm,设d为圆心到直线的距离,
(1)当d=3cm时,则⊙O与直线的位置关系是_____.
(2)当d=2cm时,则⊙O与直线的位置关系是_____.
(3)当d=1cm时,则⊙O与直线的位置关系是_____.
·o
=2cm
自 主 探 究
2、直线和圆的位置关系
数量特征
做一做
依据题目条件画出直线 ,并回答相关问题:
·
·
·
d=3cm 相离
d=2cm 相切
d=1cm 相交
自 主 探 究
=2cm
方 法 归 纳
第二种判定方法:数量法
①直线与圆相离 d > r
②直线与圆相切 d = r
③直线与圆相交 d < r
第一种判定方法:(根据公共点的个数)定义法
(1)圆与直线没有公共点 相离
(2)圆与直线只有一个公共点 相切
(3)圆与直线有两个公共点 相交
直线和圆的位置关系的判定方法
例2 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm, 以C为圆心、 r为半径作圆.
(1)当r满足____________时, ⊙C与直线AB相离;
(2)当r满足____________时, ⊙C与直线AB相切;
(3)当r满足____________时, ⊙C与AB相交.
例 题 讲 解
变式:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm, 以C为圆心、 r 为半径作圆. 当r满足__________________ 时, ⊙C与斜边AB只有一个公共点.
训 练 做 学
1.已知⊙O的半径为5cm, 点O到直线a的距离为3cm, 则⊙O与直线a的位置关系是_____,直线a与⊙O的公共 点个数是_______.
2.已知⊙O的直径是4cm, 点O到直线a的距离是2cm, 则⊙O与直线a的位置关系是______, 直线a与⊙O的公共 点个数是_______.
3.已知⊙O的半径为5cm,圆心O与直线AB的距离为 d, 根据下列条件填写d的范围:
(1)若AB和⊙O相离,则 ;
(2)若AB和⊙O相切, 则 ;
(3)若AB和⊙O相交, 则 .
基础训练
已知Rt△ABC的斜边AB=6cm,直角边 AC=3cm。
2、若圆心C,半径分别为2cm、4cm的两个圆和直线AB有怎样的位置关系?半径多长时,直线AB与⊙C相切?
A
B
C
D
提高训练
训 练 做 学
1、若圆心为A,半径分别为2cm、4cm的两个圆与直线BC有怎样的位置关系?半径多长时,BC与⊙A相切?
课 堂 小 结
说一说,本节课你有哪些收获?
图 形
公共点个数
公共点名称
直线名称
直线与圆的 位置关系
圆心到直线距离d与半径r的关系
2
0
1
交 点
切 点
割 线
切 线
相 交
相 切
相 离
dd =r
d >r
O
E
F
N
d
r
O
D
d
r
N
O
r
A
N
d
课 堂 小 结
知识要点
第二种判定方法:数量法
第一种判定方法:(根据公共点的个数)定义法
①直线与圆相离 d> r
②直线与圆相切 d= r
③直线与圆相交 d< r
课 堂 小 结
判定方法
作 业 布 置
必做题:在△ABC中, ∠A=45°,AC=4,以C为圆心、 r为 半径的圆与直线AB有怎样的位置关系?说明理由。
(1)r=2; (2)r=; (3)r=3
C
A
B
AC= 4
思考题:直线m上一点A到圆心O的距离等于⊙O的半径, 则 直线m与⊙O的位置关系是 .
感
谢
倾
听
直
线
与
圆
的位置关系
初中数学华东师范大学出版社九年级下册
27.2
复
习
提
问
2.怎样判定点和圆的位置关系?
1.点和圆有几种位置关系?
⑴点在圆内
⑵点在圆上
⑶点在圆外
d
d>r
·
·
·
·
·
d表示点到圆心O的距离
若将点改为直线,那么直线与圆的位置关系又如何呢?
一.
情 景 引 入
探 索 新 知
观察与思考
在太阳升起过程中,太阳和海平面会有那些的位置关系?
1、如果我们把太阳看作一个圆,海平面看作一条直线,请同学们利用手中的工具再现太阳升起的整个过程。(在纸上画一个圆,把你手中的笔看作一条直线,在纸上移动笔)
探究思考
3、你分类的依据是什么?
2、再现过程中,你认为直线与圆的位置关系可以分为哪几类?请在白纸上画出图形。
探 索 新 知
(3)圆与直线有两个公共点
·
·
(2)圆与直线只有一个公共点
·
(1)圆与直线没有公共点
探 索 新 知
1、直线和圆的位置关系
用公共点的个数来区分
(1)直线与圆有两个公共点,称为直线
与圆相交,两个点叫交点,这条直线叫做
的割线 。
(2)直线与圆只有一个公共点,称为直线
与圆相切,这个公共点叫切点,这条直线
圆的切线。
(3)直线与圆没有公共点,称为直线与圆相离。
交点
割线
切
线
切点
A
B
·
·
·o
·
·o
·o
归纳新知
请列举出生活中有关直线和圆的位置关系的实例。
生活实例
新知巩固
练一练
下列说法是否正确,不正确的请改正。
① 若C为⊙O内一点, 则直线CO与⊙O相交。( )
② 直线和圆有一个公共点,直线与圆相切。 ( )
③ 直线与圆最多有两个公共点。( )
④ 若A、B是⊙O外两点, 则直线AB与⊙O相离。( )
√
√
×
√
新知巩固
我指你答
·o
·o
·o
·o
·o
探索新知
除了用公共点的个数来区分直线与圆的位置关系外,能否像点和圆的位置关系一样,用数量关系的方法来判断直线与圆的位置关系?
思考
?
小 组 合 作 探 究
2、直线和圆的位置关系
数量特征
:圆心到直线的距离 :圆的半径
·o
·o
·o
·o
相 交
相 切
相 离
d < r
d = r
d > r
由圆心到直线的距离d和圆半径r间的数量关系可以判定直线与圆的位置关系,反过来
思考:由直线与圆的位置关系可以得到d与r间的数量关系吗?
动画观察
2、直线和圆的位置关系
数量特征
思考:由直线与圆的位置关系可以得到d与r间的数量关系吗?
画一画
依据题目条件画出直线 ,并回答相关问题:
如图,⊙O的半径为2cm,设d为圆心到直线的距离,
(1)当d=3cm时,则⊙O与直线的位置关系是_____.
(2)当d=2cm时,则⊙O与直线的位置关系是_____.
(3)当d=1cm时,则⊙O与直线的位置关系是_____.
·o
=2cm
自 主 探 究
2、直线和圆的位置关系
数量特征
做一做
依据题目条件画出直线 ,并回答相关问题:
·
·
·
d=3cm 相离
d=2cm 相切
d=1cm 相交
自 主 探 究
=2cm
方 法 归 纳
第二种判定方法:数量法
①直线与圆相离 d > r
②直线与圆相切 d = r
③直线与圆相交 d < r
第一种判定方法:(根据公共点的个数)定义法
(1)圆与直线没有公共点 相离
(2)圆与直线只有一个公共点 相切
(3)圆与直线有两个公共点 相交
直线和圆的位置关系的判定方法
例2 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm, 以C为圆心、 r为半径作圆.
(1)当r满足____________时, ⊙C与直线AB相离;
(2)当r满足____________时, ⊙C与直线AB相切;
(3)当r满足____________时, ⊙C与AB相交.
例 题 讲 解
变式:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm, 以C为圆心、 r 为半径作圆. 当r满足__________________ 时, ⊙C与斜边AB只有一个公共点.
训 练 做 学
1.已知⊙O的半径为5cm, 点O到直线a的距离为3cm, 则⊙O与直线a的位置关系是_____,直线a与⊙O的公共 点个数是_______.
2.已知⊙O的直径是4cm, 点O到直线a的距离是2cm, 则⊙O与直线a的位置关系是______, 直线a与⊙O的公共 点个数是_______.
3.已知⊙O的半径为5cm,圆心O与直线AB的距离为 d, 根据下列条件填写d的范围:
(1)若AB和⊙O相离,则 ;
(2)若AB和⊙O相切, 则 ;
(3)若AB和⊙O相交, 则 .
基础训练
已知Rt△ABC的斜边AB=6cm,直角边 AC=3cm。
2、若圆心C,半径分别为2cm、4cm的两个圆和直线AB有怎样的位置关系?半径多长时,直线AB与⊙C相切?
A
B
C
D
提高训练
训 练 做 学
1、若圆心为A,半径分别为2cm、4cm的两个圆与直线BC有怎样的位置关系?半径多长时,BC与⊙A相切?
课 堂 小 结
说一说,本节课你有哪些收获?
图 形
公共点个数
公共点名称
直线名称
直线与圆的 位置关系
圆心到直线距离d与半径r的关系
2
0
1
交 点
切 点
割 线
切 线
相 交
相 切
相 离
d
d >r
O
E
F
N
d
r
O
D
d
r
N
O
r
A
N
d
课 堂 小 结
知识要点
第二种判定方法:数量法
第一种判定方法:(根据公共点的个数)定义法
①直线与圆相离 d> r
②直线与圆相切 d= r
③直线与圆相交 d< r
课 堂 小 结
判定方法
作 业 布 置
必做题:在△ABC中, ∠A=45°,AC=4,以C为圆心、 r为 半径的圆与直线AB有怎样的位置关系?说明理由。
(1)r=2; (2)r=; (3)r=3
C
A
B
AC= 4
思考题:直线m上一点A到圆心O的距离等于⊙O的半径, 则 直线m与⊙O的位置关系是 .
感
谢
倾
听
