2021-2022学年人教版七年级数学上册4.1.2 从不同方向看立体图形 课时训练(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册4.1.2 从不同方向看立体图形 课时训练(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 293.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-13 00:00:00 | ||
图片预览


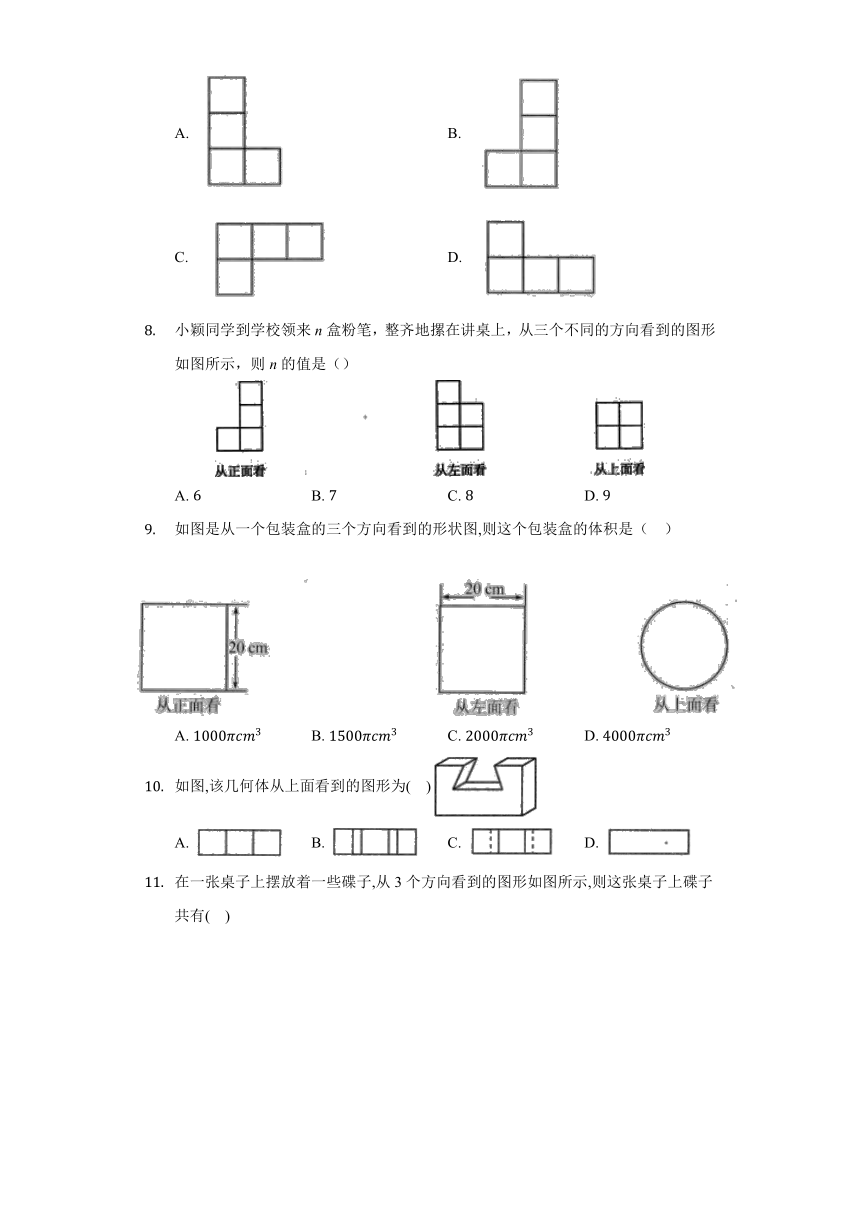
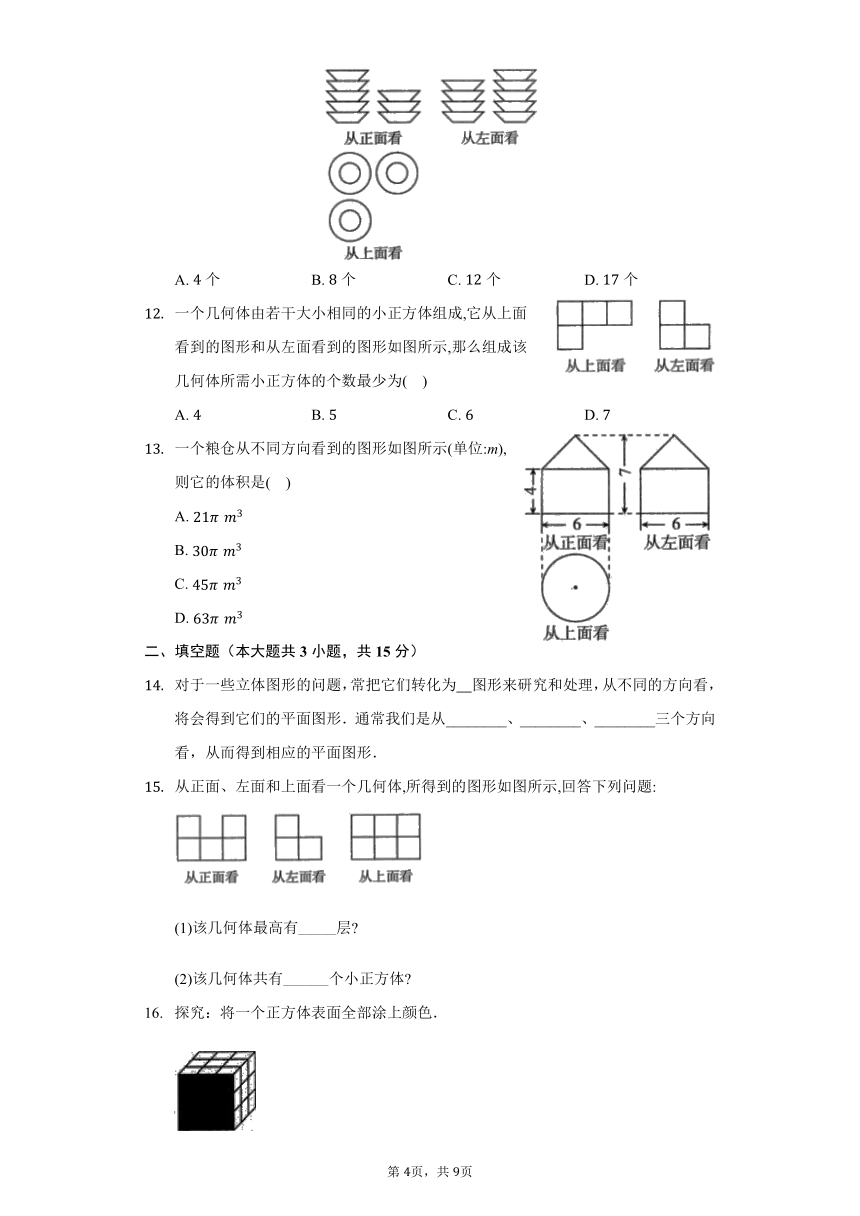

文档简介
4.1.2 从不同方向看立体图形课时训练
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共13小题,共39分)
如图是某几何体从上面看得到的图形,该几何体可能是( )
A. 圆柱
B. 圆锥
C. 球
D. 正方体
下列四个几何体的俯视图中与众不同的是( )
A. B.
C. D.
如图,空心圆柱的左视图是( )
A. B.
C. D.
一个几何体从三个方向看得到的图形如图所示,则这个几何体是( )
A. 三棱锥 B. 三棱柱 C. 圆柱 D. 长方体
如图所示的立体图形,从上面看到的图形是( )
A. B.
C. D.
下面四个几何体中,从左面看到的图形是四边形的几何体的个数共有( )
A. 个 B. 个 C. 个 D. 个
由7个大小相同的小正方体组合成一个几何体,其从上往下看得到的平面图形如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则从左面看得到的平面图形是( )
A. B.
C. D.
小颖同学到学校领来n盒粉笔,整齐地摞在讲桌上,从三个不同的方向看到的图形如图所示,则n的值是()
A. B. C. D.
如图是从一个包装盒的三个方向看到的形状图,则这个包装盒的体积是( )
A. B. C. D.
如图,该几何体从上面看到的图形为( )
A. B. C. D.
在一张桌子上摆放着一些碟子,从3个方向看到的图形如图所示,则这张桌子上碟子共有( )
A. 个 B. 个 C. 个 D. 个
一个几何体由若干大小相同的小正方体组成,它从上面看到的图形和从左面看到的图形如图所示,那么组成该几何体所需小正方体的个数最少为( )
A. B. C. D.
一个粮仓从不同方向看到的图形如图所示(单位:m),则它的体积是( )
A.
B.
C.
D.
二、填空题(本大题共3小题,共15分)
对于一些立体图形的问题,常把它们转化为 图形来研究和处理,从不同的方向看,将会得到它们的平面图形.通常我们是从________、________、________三个方向看,从而得到相应的平面图形.
从正面、左面和上面看一个几何体,所得到的图形如图所示,回答下列问题:
(1)该几何体最高有_____层
(2)该几何体共有______个小正方体
探究:将一个正方体表面全部涂上颜色.
(1)把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体,我们把仅有i个面涂色的小正方体的个数记为xi,那么x3=________,x2=________,x1=________,x0=________;
(2)如果把正方体的棱四等分,同样沿等分线把正方体切开,得到64个小正方体,那么x3=________,x2=________,x1=________,x0=________;
(3)如果把正方体的棱n等分(n≥3),然后沿等分线把正方体切开,得到n3个小正方体,那么x3=________,x2=________,x1=________,x0=________.
三、解答题(本大题共3小题,共46分)
如图,小红,小明,小芳三人站在不同的位置给一个立体图形照相,哪幅图是他们照到的 填一填.
如图是由8个相同的小立方块搭成的几何体,已知它的左视图如下,请画出它的主视图和俯视图.
主视图:
左视图:
俯视图:
如图是从一个几何体的正面和上面看到的图形,求该几何体的体积.(取3.14)
参考答案
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】B
9.【答案】C
10.【答案】C
11.【答案】C
12.【答案】B
13.【答案】C
14.【答案】平面;正面;上面;左面
15.【答案】解:(1)该几何体最高有2层;
(2)该几何体共有8个小正方体.
16.【答案】(1)8;12;6;1
(2)8;24;24;8
(3)8;12(n-2);6(n-2)2;(n-2)3
17.【答案】解:小明照到的是
小红照到的是
小芳照到的是
18.【答案】解:如图所示:
19.【答案】解:该几何体由圆柱和长方体组成,所以它的体积就是长方体的体积加圆柱的体积.
长方体的体积为253040=30000(),
圆柱的体积为π32=10048(),
所以该几何体的体积=长方体的体积+圆柱的体积=30000+10048=40048().
第8页,共8页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共13小题,共39分)
如图是某几何体从上面看得到的图形,该几何体可能是( )
A. 圆柱
B. 圆锥
C. 球
D. 正方体
下列四个几何体的俯视图中与众不同的是( )
A. B.
C. D.
如图,空心圆柱的左视图是( )
A. B.
C. D.
一个几何体从三个方向看得到的图形如图所示,则这个几何体是( )
A. 三棱锥 B. 三棱柱 C. 圆柱 D. 长方体
如图所示的立体图形,从上面看到的图形是( )
A. B.
C. D.
下面四个几何体中,从左面看到的图形是四边形的几何体的个数共有( )
A. 个 B. 个 C. 个 D. 个
由7个大小相同的小正方体组合成一个几何体,其从上往下看得到的平面图形如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则从左面看得到的平面图形是( )
A. B.
C. D.
小颖同学到学校领来n盒粉笔,整齐地摞在讲桌上,从三个不同的方向看到的图形如图所示,则n的值是()
A. B. C. D.
如图是从一个包装盒的三个方向看到的形状图,则这个包装盒的体积是( )
A. B. C. D.
如图,该几何体从上面看到的图形为( )
A. B. C. D.
在一张桌子上摆放着一些碟子,从3个方向看到的图形如图所示,则这张桌子上碟子共有( )
A. 个 B. 个 C. 个 D. 个
一个几何体由若干大小相同的小正方体组成,它从上面看到的图形和从左面看到的图形如图所示,那么组成该几何体所需小正方体的个数最少为( )
A. B. C. D.
一个粮仓从不同方向看到的图形如图所示(单位:m),则它的体积是( )
A.
B.
C.
D.
二、填空题(本大题共3小题,共15分)
对于一些立体图形的问题,常把它们转化为 图形来研究和处理,从不同的方向看,将会得到它们的平面图形.通常我们是从________、________、________三个方向看,从而得到相应的平面图形.
从正面、左面和上面看一个几何体,所得到的图形如图所示,回答下列问题:
(1)该几何体最高有_____层
(2)该几何体共有______个小正方体
探究:将一个正方体表面全部涂上颜色.
(1)把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体,我们把仅有i个面涂色的小正方体的个数记为xi,那么x3=________,x2=________,x1=________,x0=________;
(2)如果把正方体的棱四等分,同样沿等分线把正方体切开,得到64个小正方体,那么x3=________,x2=________,x1=________,x0=________;
(3)如果把正方体的棱n等分(n≥3),然后沿等分线把正方体切开,得到n3个小正方体,那么x3=________,x2=________,x1=________,x0=________.
三、解答题(本大题共3小题,共46分)
如图,小红,小明,小芳三人站在不同的位置给一个立体图形照相,哪幅图是他们照到的 填一填.
如图是由8个相同的小立方块搭成的几何体,已知它的左视图如下,请画出它的主视图和俯视图.
主视图:
左视图:
俯视图:
如图是从一个几何体的正面和上面看到的图形,求该几何体的体积.(取3.14)
参考答案
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】B
9.【答案】C
10.【答案】C
11.【答案】C
12.【答案】B
13.【答案】C
14.【答案】平面;正面;上面;左面
15.【答案】解:(1)该几何体最高有2层;
(2)该几何体共有8个小正方体.
16.【答案】(1)8;12;6;1
(2)8;24;24;8
(3)8;12(n-2);6(n-2)2;(n-2)3
17.【答案】解:小明照到的是
小红照到的是
小芳照到的是
18.【答案】解:如图所示:
19.【答案】解:该几何体由圆柱和长方体组成,所以它的体积就是长方体的体积加圆柱的体积.
长方体的体积为253040=30000(),
圆柱的体积为π32=10048(),
所以该几何体的体积=长方体的体积+圆柱的体积=30000+10048=40048().
第8页,共8页
