24.2 点和圆、直线与圆的位置关系 同步分层作业(含解析)
文档属性
| 名称 | 24.2 点和圆、直线与圆的位置关系 同步分层作业(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-13 21:27:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2021年九年级上册数学分层作业
---点和圆、直线与圆的位置关系
一.选择题(共7小题)
1.如图,点A在半径为3的⊙O内,OA=,P为⊙O上一点,延长PO、PA交⊙O于M、N.当MN取最大值时,PA的长等于( )
A. B. C. D.
2.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.① B.② C.③ D.④
3.如图,⊙O是△ABC的外接圆,∠CAB=30°,∠ACB=105°,CD⊥AB于点D且CD=2,则⊙O的半径为( )
A.2 B.4 C.4 D.4
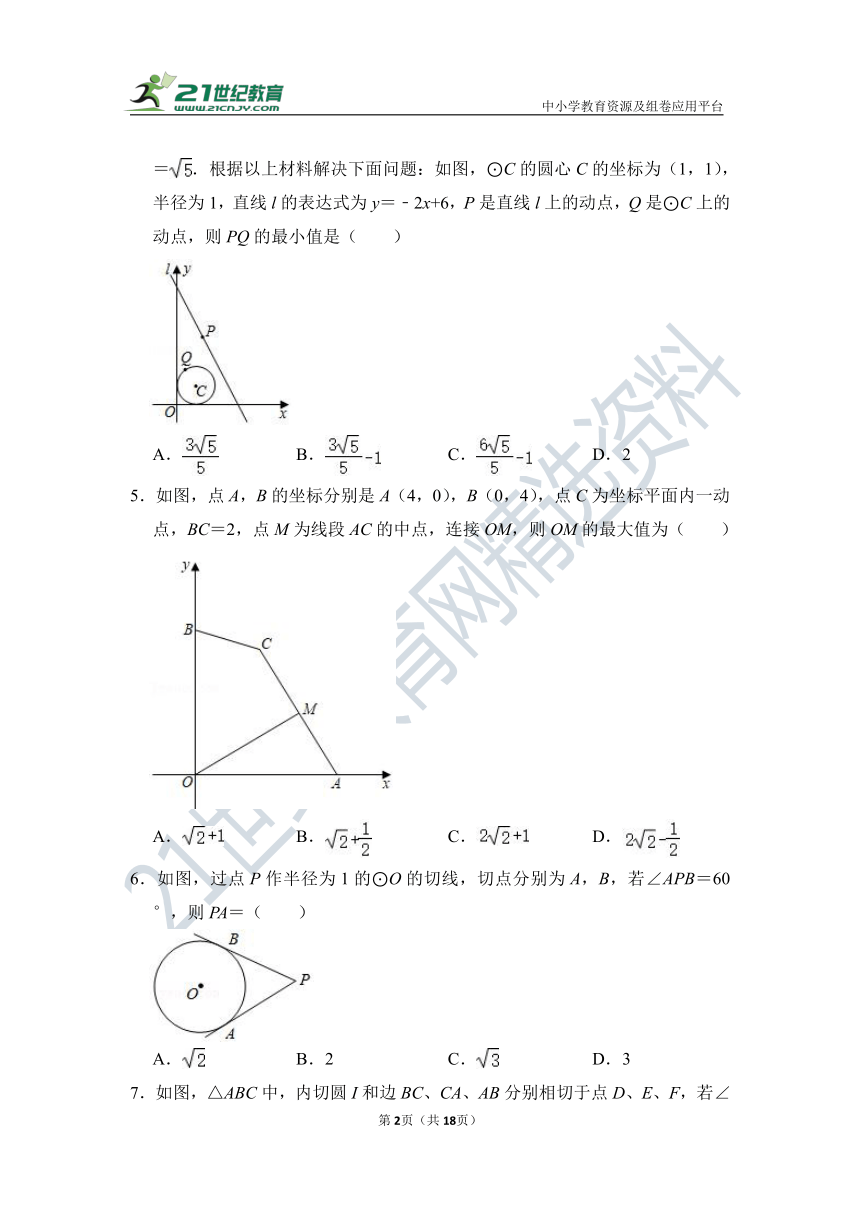
4.已知点P(x0,y0)和直线y=kx+b,求点P到直线y=kx+b的距离d可用公式计算.例如:点(0,1)到直线y=2x+6的距离d==.根据以上材料解决下面问题:如图,⊙C的圆心C的坐标为(1,1),半径为1,直线l的表达式为y=﹣2x+6,P是直线l上的动点,Q是⊙C上的动点,则PQ的最小值是( )
A. B. C. D.2
5.如图,点A,B的坐标分别是A(4,0),B(0,4),点C为坐标平面内一动点,BC=2,点M为线段AC的中点,连接OM,则OM的最大值为( )
A. B. C. D.
6.如图,过点P作半径为1的⊙O的切线,切点分别为A,B,若∠APB=60°,则PA=( )
A. B.2 C. D.3
7.如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠B=60°,∠C=70°,则∠EDF的度数是( )
A.60° B.130° C.50° D.65°
二.填空题(共5小题)
8.一个已知点P到圆周上的最长距离是7,最短距离是3,则此圆的半径是 .
9.如图,正方形ABCD的边长为4,点E是AB边上一个动点,点F是CD边上一个动点,且AE=CF,过点B作BG⊥EF于点G,连接AG,则AG长的最小值是 .
10.已知⊙O的半径为5cm,A为线段OB的中点,当OB=9cm时,点A在⊙O .
11.平面直角坐标系内的三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3), 确定一个圆,(填“能”或“不能”).
12.锐角△ABC,其外接圆圆心为O,AB、AC上的高交于H,若O、H、B、C在同一圆周上,则∠BAC= .
三.解答题(共3小题)
13.如图,直角三角形ABC中,∠ABC=90°,D为AB上一点,以BD为直径作⊙O,CD与⊙O交于点E,延长AE与BC交于点F,且CF=BF.
(1)求证:AF与⊙O相切;
(2)若AB=8,BC=12,求⊙O半径.
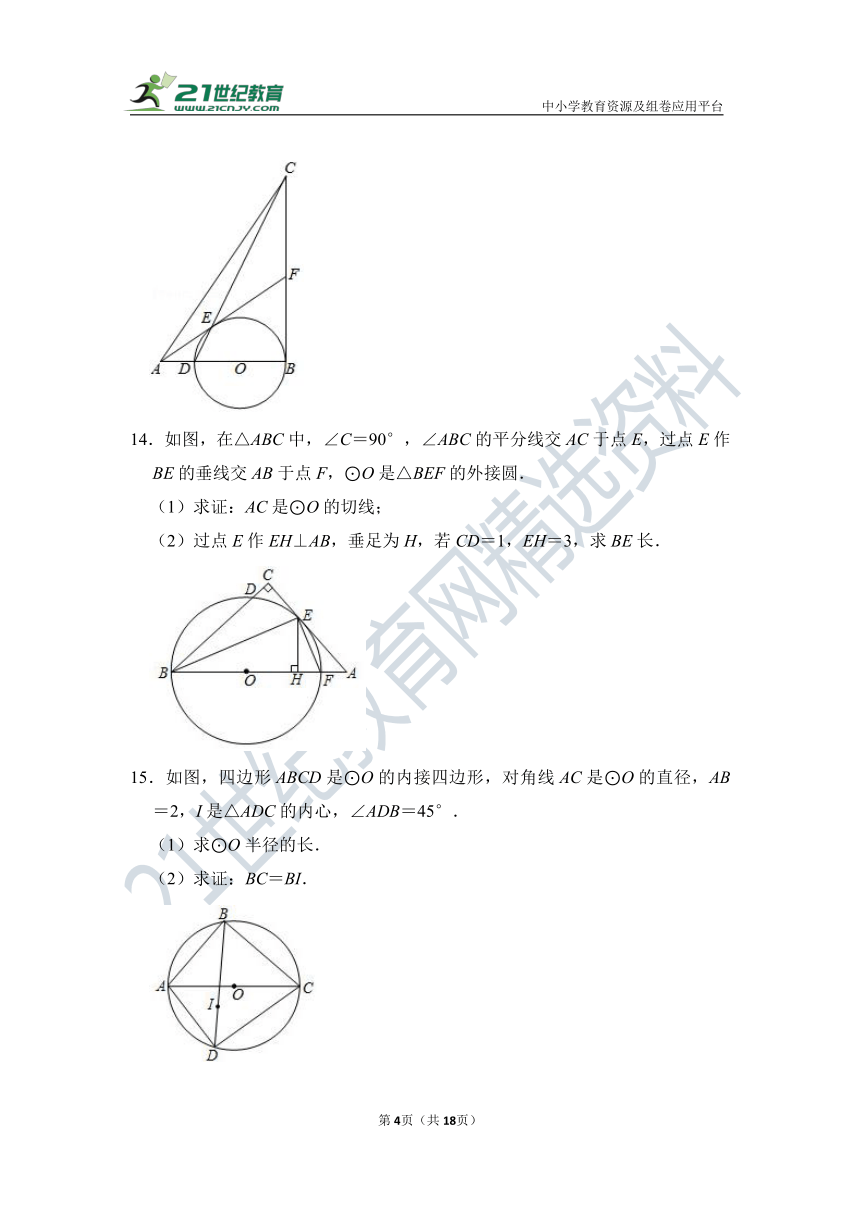
14.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,若CD=1,EH=3,求BE长.
15.如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,I是△ADC的内心,∠ADB=45°.
(1)求⊙O半径的长.
(2)求证:BC=BI.
2021年九年级上册数学分层作业---点和圆、直线与圆的位置关系
参考答案与试题解析
一.选择题(共7小题)
1.如图,点A在半径为3的⊙O内,OA=,P为⊙O上一点,延长PO、PA交⊙O于M、N.当MN取最大值时,PA的长等于( )
A. B. C. D.
【解答】解:当OA⊥PN时,MN的值最大,
在Rt△POA中,由勾股定理得,
PA===,
故选:C.
2.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.① B.② C.③ D.④
【解答】解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
3.如图,⊙O是△ABC的外接圆,∠CAB=30°,∠ACB=105°,CD⊥AB于点D且CD=2,则⊙O的半径为( )
A.2 B.4 C.4 D.4
【解答】解:如图,连接OA,OC,
∵CD⊥AB,
∴∠ADC=90°,
∵∠CAB=30°,CD=2,
∴AC=2CD=4,
∵∠ACB=105°,∠ACD=60°,
∴∠CBA=45°,
∵∠COA=2∠CBA=2×45°=90°,
在Rt△AOC中,由勾股定理得:AC2=OA2+OC2,
∵OA=OC,
∴OA=AC=4,
∴⊙O的半径为4,
故选:B.
4.已知点P(x0,y0)和直线y=kx+b,求点P到直线y=kx+b的距离d可用公式计算.例如:点(0,1)到直线y=2x+6的距离d==.根据以上材料解决下面问题:如图,⊙C的圆心C的坐标为(1,1),半径为1,直线l的表达式为y=﹣2x+6,P是直线l上的动点,Q是⊙C上的动点,则PQ的最小值是( )
A. B. C. D.2
【解答】解:过点C作CP⊥直线l,交圆C于Q点,此时PQ的值最小,
根据点到直线的距离公式可知:点C(1,1)到直线l的距离d==,
∵⊙C的半径为1,
∴PQ=﹣1,
故选:B.
5.如图,点A,B的坐标分别是A(4,0),B(0,4),点C为坐标平面内一动点,BC=2,点M为线段AC的中点,连接OM,则OM的最大值为( )
A. B. C. D.
【解答】解:如图,∵点C为坐标平面内一点,BC=2,
∴C在⊙B上,且半径为2,
取OD=OA=4,连接CD,
∵AM=CM,OD=OA,
∴OM是△ACD的中位线,
∴OM=CD,
当OM最大时,即CD最大,而D,B,C三点共线时,当C在DB的延长线上时,OM最大,
∵OB=OD=4,∠BOD=90°,
∴BD=4,
∴CD=4+2,
∴OM=CD=2+1,即OM的最大值为2+1;
故选:C.
6.如图,过点P作半径为1的⊙O的切线,切点分别为A,B,若∠APB=60°,则PA=( )
A. B.2 C. D.3
【解答】解:连接OA,OB,OP,
∵PA,PB是⊙O的切线,
∴PA⊥OA,∠APO=∠BPO,
∵∠APB=60°,
∴∠APO=30°,
∵OA=1,
∴PA=OA=.
故选:C.
7.如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠B=60°,∠C=70°,则∠EDF的度数是( )
A.60° B.130° C.50° D.65°
【解答】解:连接IF,IE,
∵∠B=60°,∠C=70°,
∴∠A=180°﹣60°﹣70°=50°
∵内切圆I与边BC、CA、AB分别相切于点D、E、F,
∴IF⊥AB,IE⊥AC,
∵∠A=50°,
∴∠FIE=130°,
∴∠EDF===65°.
故选:D.
二.填空题(共5小题)
8.一个已知点P到圆周上的最长距离是7,最短距离是3,则此圆的半径是 2或5 .
【解答】解:①当点在圆外时,
∵圆外一点和圆周的最短距离为3,最长距离为7,
∴圆的直径为7﹣3=4,
∴该圆的半径是2;
②当点在圆内时,
∵点到圆周的最短距离为3,最长距离为7,
∴圆的直径=7+3=10,
∴圆的半径为5,
故答案为2或5.
9.如图,正方形ABCD的边长为4,点E是AB边上一个动点,点F是CD边上一个动点,且AE=CF,过点B作BG⊥EF于点G,连接AG,则AG长的最小值是 ﹣ .
【解答】解:设正方形的中心为O,可证EF经过O点.
连接OB,取OB中点M,连接 MA,MG,则MA,MG为定长,过点M作MH⊥AB于H.则MH=BH=1,AH=3,
由勾股定理可得MA=,MG=OB=,
∵AG≥AM﹣MG=﹣,
当A,M,G三点共线时,AG最小=﹣,
故答案为:﹣.
10.已知⊙O的半径为5cm,A为线段OB的中点,当OB=9cm时,点A在⊙O 内 .
【解答】解:A为线段OB的中点,当OB=9cm时,得OA=OB=4.5(cm),
∵r=5cm,
∴d<r,
∴点A与⊙O的位置关系是点A在圆O内,
故答案为:内.
11.平面直角坐标系内的三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3), 不能 确定一个圆,(填“能”或“不能”).
【解答】解:∵B(0,﹣3)、C(2,﹣3),A(1,﹣3),
∴点A、B、C共线,
∴三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3)不能确定一个圆.
故答案为:不能.
12.锐角△ABC,其外接圆圆心为O,AB、AC上的高交于H,若O、H、B、C在同一圆周上,则∠BAC= 60° .
【解答】解:如图,连接OB,OC,
∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
∴∠BAC+∠DHE=360°﹣∠ADC﹣∠AEB=180°,
∵O、H、B、C在同一圆周上,
∴∠BOC=∠BHC=∠DHE,
∴∠BAC+∠BOC=180°,
∵∠BOC=2∠BAC,
∴∠BAC+∠BOC=3∠BAC=180°,
∴∠BAC=60°,
故答案为:60°.
三.解答题(共3小题)
13.如图,直角三角形ABC中,∠ABC=90°,D为AB上一点,以BD为直径作⊙O,CD与⊙O交于点E,延长AE与BC交于点F,且CF=BF.
(1)求证:AF与⊙O相切;
(2)若AB=8,BC=12,求⊙O半径.
【解答】解:(1)如图,连接OE,BE,
∵BD为⊙O的直径,
∴∠BED=90°,
∴∠BEC=90°,
∵CF=FB,
∴EF=CB=FB,
∴∠FEB=∠FBE,
∵OE=OB,
∴∠OEB=∠OBE,
∵∠OBE+∠FBE=∠OBF=90°,
∴∠OEB+∠FEB=∠OEF=90°,
∵OE是⊙O的半径,
∴AF与⊙O相切;
(2)∵AB=8,BC=12,
∴EF=FB=CB=6,
∴AF===10,
∴AE=AF﹣EF=10﹣6=4,
∵OE=OB,
∴OA=AB﹣OB=8﹣OE,
∵AE2+OE2=OA2,
∴42+OE2=(8﹣OE)2,
解得OE=3.
∴⊙O半径为3.
14.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,若CD=1,EH=3,求BE长.
【解答】解:(1)证明:
连接OE,
∵BE平分∠ABC,
∴∠CBE=∠ABE
又OB=OE,∠ABE=∠BEO,
∴∠CBE=∠BEO
∴OE∥BC
又∠C=90°
即AC⊥BC.
∴OE⊥AC,
即AC是⊙O的切线;
(2)连接DE,
∵AE平分∠ABC,AC⊥BC、EH⊥AB
∴CE=EH,DE=EF,
∴Rt△CDE≌Rt△HFE(HL),
∴CD=HF,
∵CD=1,
∴HF=1
∵OH=3,
∵OE2=OH2+HE2,
∴OE2=(OE﹣1)2+32
解得:0E=5,
∴BH=9
∴.
15.如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,I是△ADC的内心,∠ADB=45°.
(1)求⊙O半径的长.
(2)求证:BC=BI.
【解答】解:(1)∵AC是⊙的直径,
∴∠ADC=90°=∠ABC,
又∠ADB=45°,
∴∠ADB=∠BDC=45°,
∴,
∴AB=BC
∵AB=2,
∴
∴⊙O的半径为;
(2)连接AI,
∵I是△ADC的内心.
∴∠DAI=∠CAI,
∠AIB=∠DAI+∠ADI,
∠BAI=∠BAC+∠CAI,
∵∠BAC=∠ADI,
∴∠BAI=∠AIB,
∴AB=BI,
即BC=BI.
第1页(共1页)
2021年九年级上册数学分层作业
---点和圆、直线与圆的位置关系
一.选择题(共7小题)
1.如图,点A在半径为3的⊙O内,OA=,P为⊙O上一点,延长PO、PA交⊙O于M、N.当MN取最大值时,PA的长等于( )
A. B. C. D.
2.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.① B.② C.③ D.④
3.如图,⊙O是△ABC的外接圆,∠CAB=30°,∠ACB=105°,CD⊥AB于点D且CD=2,则⊙O的半径为( )
A.2 B.4 C.4 D.4
4.已知点P(x0,y0)和直线y=kx+b,求点P到直线y=kx+b的距离d可用公式计算.例如:点(0,1)到直线y=2x+6的距离d==.根据以上材料解决下面问题:如图,⊙C的圆心C的坐标为(1,1),半径为1,直线l的表达式为y=﹣2x+6,P是直线l上的动点,Q是⊙C上的动点,则PQ的最小值是( )
A. B. C. D.2
5.如图,点A,B的坐标分别是A(4,0),B(0,4),点C为坐标平面内一动点,BC=2,点M为线段AC的中点,连接OM,则OM的最大值为( )
A. B. C. D.
6.如图,过点P作半径为1的⊙O的切线,切点分别为A,B,若∠APB=60°,则PA=( )
A. B.2 C. D.3
7.如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠B=60°,∠C=70°,则∠EDF的度数是( )
A.60° B.130° C.50° D.65°
二.填空题(共5小题)
8.一个已知点P到圆周上的最长距离是7,最短距离是3,则此圆的半径是 .
9.如图,正方形ABCD的边长为4,点E是AB边上一个动点,点F是CD边上一个动点,且AE=CF,过点B作BG⊥EF于点G,连接AG,则AG长的最小值是 .
10.已知⊙O的半径为5cm,A为线段OB的中点,当OB=9cm时,点A在⊙O .
11.平面直角坐标系内的三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3), 确定一个圆,(填“能”或“不能”).
12.锐角△ABC,其外接圆圆心为O,AB、AC上的高交于H,若O、H、B、C在同一圆周上,则∠BAC= .
三.解答题(共3小题)
13.如图,直角三角形ABC中,∠ABC=90°,D为AB上一点,以BD为直径作⊙O,CD与⊙O交于点E,延长AE与BC交于点F,且CF=BF.
(1)求证:AF与⊙O相切;
(2)若AB=8,BC=12,求⊙O半径.
14.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,若CD=1,EH=3,求BE长.
15.如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,I是△ADC的内心,∠ADB=45°.
(1)求⊙O半径的长.
(2)求证:BC=BI.
2021年九年级上册数学分层作业---点和圆、直线与圆的位置关系
参考答案与试题解析
一.选择题(共7小题)
1.如图,点A在半径为3的⊙O内,OA=,P为⊙O上一点,延长PO、PA交⊙O于M、N.当MN取最大值时,PA的长等于( )
A. B. C. D.
【解答】解:当OA⊥PN时,MN的值最大,
在Rt△POA中,由勾股定理得,
PA===,
故选:C.
2.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.① B.② C.③ D.④
【解答】解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
3.如图,⊙O是△ABC的外接圆,∠CAB=30°,∠ACB=105°,CD⊥AB于点D且CD=2,则⊙O的半径为( )
A.2 B.4 C.4 D.4
【解答】解:如图,连接OA,OC,
∵CD⊥AB,
∴∠ADC=90°,
∵∠CAB=30°,CD=2,
∴AC=2CD=4,
∵∠ACB=105°,∠ACD=60°,
∴∠CBA=45°,
∵∠COA=2∠CBA=2×45°=90°,
在Rt△AOC中,由勾股定理得:AC2=OA2+OC2,
∵OA=OC,
∴OA=AC=4,
∴⊙O的半径为4,
故选:B.
4.已知点P(x0,y0)和直线y=kx+b,求点P到直线y=kx+b的距离d可用公式计算.例如:点(0,1)到直线y=2x+6的距离d==.根据以上材料解决下面问题:如图,⊙C的圆心C的坐标为(1,1),半径为1,直线l的表达式为y=﹣2x+6,P是直线l上的动点,Q是⊙C上的动点,则PQ的最小值是( )
A. B. C. D.2
【解答】解:过点C作CP⊥直线l,交圆C于Q点,此时PQ的值最小,
根据点到直线的距离公式可知:点C(1,1)到直线l的距离d==,
∵⊙C的半径为1,
∴PQ=﹣1,
故选:B.
5.如图,点A,B的坐标分别是A(4,0),B(0,4),点C为坐标平面内一动点,BC=2,点M为线段AC的中点,连接OM,则OM的最大值为( )
A. B. C. D.
【解答】解:如图,∵点C为坐标平面内一点,BC=2,
∴C在⊙B上,且半径为2,
取OD=OA=4,连接CD,
∵AM=CM,OD=OA,
∴OM是△ACD的中位线,
∴OM=CD,
当OM最大时,即CD最大,而D,B,C三点共线时,当C在DB的延长线上时,OM最大,
∵OB=OD=4,∠BOD=90°,
∴BD=4,
∴CD=4+2,
∴OM=CD=2+1,即OM的最大值为2+1;
故选:C.
6.如图,过点P作半径为1的⊙O的切线,切点分别为A,B,若∠APB=60°,则PA=( )
A. B.2 C. D.3
【解答】解:连接OA,OB,OP,
∵PA,PB是⊙O的切线,
∴PA⊥OA,∠APO=∠BPO,
∵∠APB=60°,
∴∠APO=30°,
∵OA=1,
∴PA=OA=.
故选:C.
7.如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠B=60°,∠C=70°,则∠EDF的度数是( )
A.60° B.130° C.50° D.65°
【解答】解:连接IF,IE,
∵∠B=60°,∠C=70°,
∴∠A=180°﹣60°﹣70°=50°
∵内切圆I与边BC、CA、AB分别相切于点D、E、F,
∴IF⊥AB,IE⊥AC,
∵∠A=50°,
∴∠FIE=130°,
∴∠EDF===65°.
故选:D.
二.填空题(共5小题)
8.一个已知点P到圆周上的最长距离是7,最短距离是3,则此圆的半径是 2或5 .
【解答】解:①当点在圆外时,
∵圆外一点和圆周的最短距离为3,最长距离为7,
∴圆的直径为7﹣3=4,
∴该圆的半径是2;
②当点在圆内时,
∵点到圆周的最短距离为3,最长距离为7,
∴圆的直径=7+3=10,
∴圆的半径为5,
故答案为2或5.
9.如图,正方形ABCD的边长为4,点E是AB边上一个动点,点F是CD边上一个动点,且AE=CF,过点B作BG⊥EF于点G,连接AG,则AG长的最小值是 ﹣ .
【解答】解:设正方形的中心为O,可证EF经过O点.
连接OB,取OB中点M,连接 MA,MG,则MA,MG为定长,过点M作MH⊥AB于H.则MH=BH=1,AH=3,
由勾股定理可得MA=,MG=OB=,
∵AG≥AM﹣MG=﹣,
当A,M,G三点共线时,AG最小=﹣,
故答案为:﹣.
10.已知⊙O的半径为5cm,A为线段OB的中点,当OB=9cm时,点A在⊙O 内 .
【解答】解:A为线段OB的中点,当OB=9cm时,得OA=OB=4.5(cm),
∵r=5cm,
∴d<r,
∴点A与⊙O的位置关系是点A在圆O内,
故答案为:内.
11.平面直角坐标系内的三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3), 不能 确定一个圆,(填“能”或“不能”).
【解答】解:∵B(0,﹣3)、C(2,﹣3),A(1,﹣3),
∴点A、B、C共线,
∴三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3)不能确定一个圆.
故答案为:不能.
12.锐角△ABC,其外接圆圆心为O,AB、AC上的高交于H,若O、H、B、C在同一圆周上,则∠BAC= 60° .
【解答】解:如图,连接OB,OC,
∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
∴∠BAC+∠DHE=360°﹣∠ADC﹣∠AEB=180°,
∵O、H、B、C在同一圆周上,
∴∠BOC=∠BHC=∠DHE,
∴∠BAC+∠BOC=180°,
∵∠BOC=2∠BAC,
∴∠BAC+∠BOC=3∠BAC=180°,
∴∠BAC=60°,
故答案为:60°.
三.解答题(共3小题)
13.如图,直角三角形ABC中,∠ABC=90°,D为AB上一点,以BD为直径作⊙O,CD与⊙O交于点E,延长AE与BC交于点F,且CF=BF.
(1)求证:AF与⊙O相切;
(2)若AB=8,BC=12,求⊙O半径.
【解答】解:(1)如图,连接OE,BE,
∵BD为⊙O的直径,
∴∠BED=90°,
∴∠BEC=90°,
∵CF=FB,
∴EF=CB=FB,
∴∠FEB=∠FBE,
∵OE=OB,
∴∠OEB=∠OBE,
∵∠OBE+∠FBE=∠OBF=90°,
∴∠OEB+∠FEB=∠OEF=90°,
∵OE是⊙O的半径,
∴AF与⊙O相切;
(2)∵AB=8,BC=12,
∴EF=FB=CB=6,
∴AF===10,
∴AE=AF﹣EF=10﹣6=4,
∵OE=OB,
∴OA=AB﹣OB=8﹣OE,
∵AE2+OE2=OA2,
∴42+OE2=(8﹣OE)2,
解得OE=3.
∴⊙O半径为3.
14.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,若CD=1,EH=3,求BE长.
【解答】解:(1)证明:
连接OE,
∵BE平分∠ABC,
∴∠CBE=∠ABE
又OB=OE,∠ABE=∠BEO,
∴∠CBE=∠BEO
∴OE∥BC
又∠C=90°
即AC⊥BC.
∴OE⊥AC,
即AC是⊙O的切线;
(2)连接DE,
∵AE平分∠ABC,AC⊥BC、EH⊥AB
∴CE=EH,DE=EF,
∴Rt△CDE≌Rt△HFE(HL),
∴CD=HF,
∵CD=1,
∴HF=1
∵OH=3,
∵OE2=OH2+HE2,
∴OE2=(OE﹣1)2+32
解得:0E=5,
∴BH=9
∴.
15.如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,I是△ADC的内心,∠ADB=45°.
(1)求⊙O半径的长.
(2)求证:BC=BI.
【解答】解:(1)∵AC是⊙的直径,
∴∠ADC=90°=∠ABC,
又∠ADB=45°,
∴∠ADB=∠BDC=45°,
∴,
∴AB=BC
∵AB=2,
∴
∴⊙O的半径为;
(2)连接AI,
∵I是△ADC的内心.
∴∠DAI=∠CAI,
∠AIB=∠DAI+∠ADI,
∠BAI=∠BAC+∠CAI,
∵∠BAC=∠ADI,
∴∠BAI=∠AIB,
∴AB=BI,
即BC=BI.
第1页(共1页)
同课章节目录
