3.1匀变速直线运动的规律同步练习题(Word版含答案)
文档属性
| 名称 | 3.1匀变速直线运动的规律同步练习题(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 94.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-12 19:56:29 | ||
图片预览




文档简介
3.1匀变速直线运动的规律同步练习题2021-2022学年鲁科版高中必修一物理
一、单选题
一质点沿轴正方向做直线运动,通过坐标原点时开始计时,图像如图,则
A. 质点做匀速直线运动,速度为
B. 质点做匀加速直线运动,加速度为
C. 质点在末速度为
D. 质点在第内的位移为
一辆汽车遇到前方有障碍物开始刹车,刹车后的第内和第内位移大小依次为和。则下列分析正确的是
A. 汽车开始刹车时的初速度为
B. 刹车过程持续的时间为
C. 刹车最后的初速度为
D. 刹车后内的位移是
物体以初速度做匀减速直线运动,第内通过的位移为,第内通过的位移为,又经过位移物体的速度减小为,则下列说法中不正确的是
A. 加速度的大小为
B. 初速度的大小为
C. 位移的大小为
D. 位移内的平均速度大小为
如图所示,物体从点由静止开始做匀加速直线运动,途经、、三点,其中,。若物体通过和这两段位移的时间相等,则、两点之间的距离等于
A. B. C. D.
关于匀变速直线运动的公式,有下面几种说法,正确的是
A. 由公式可知,做匀变速直线运动的物体,其加速度的大小与物体运动的速度改变量成正比,与速度改变量所对应的时间成反比
B. 由公式可知,做匀变速直线运动的物体,其加速度的大小与物体运动的速度平方的改变量成正比,与物体运动的位移成反比
C. 由公式可知,做初速度为零的匀变速直线运动的物体,其位移的大小与物体运动的时间的平方成正比
D. 由公式可知,做匀变速直线运动的物体,若加速度,则物体做加速运动,若加速度,则物体做减速运动
物体从静止开始做匀加速直线运动,已知第内与第内的位移之差是,则可知
A. 物体运动的加速度大小为
B. 第末的速度大小为
C. 第内的位移大小为
D. 物体在前内的平均速度大小为
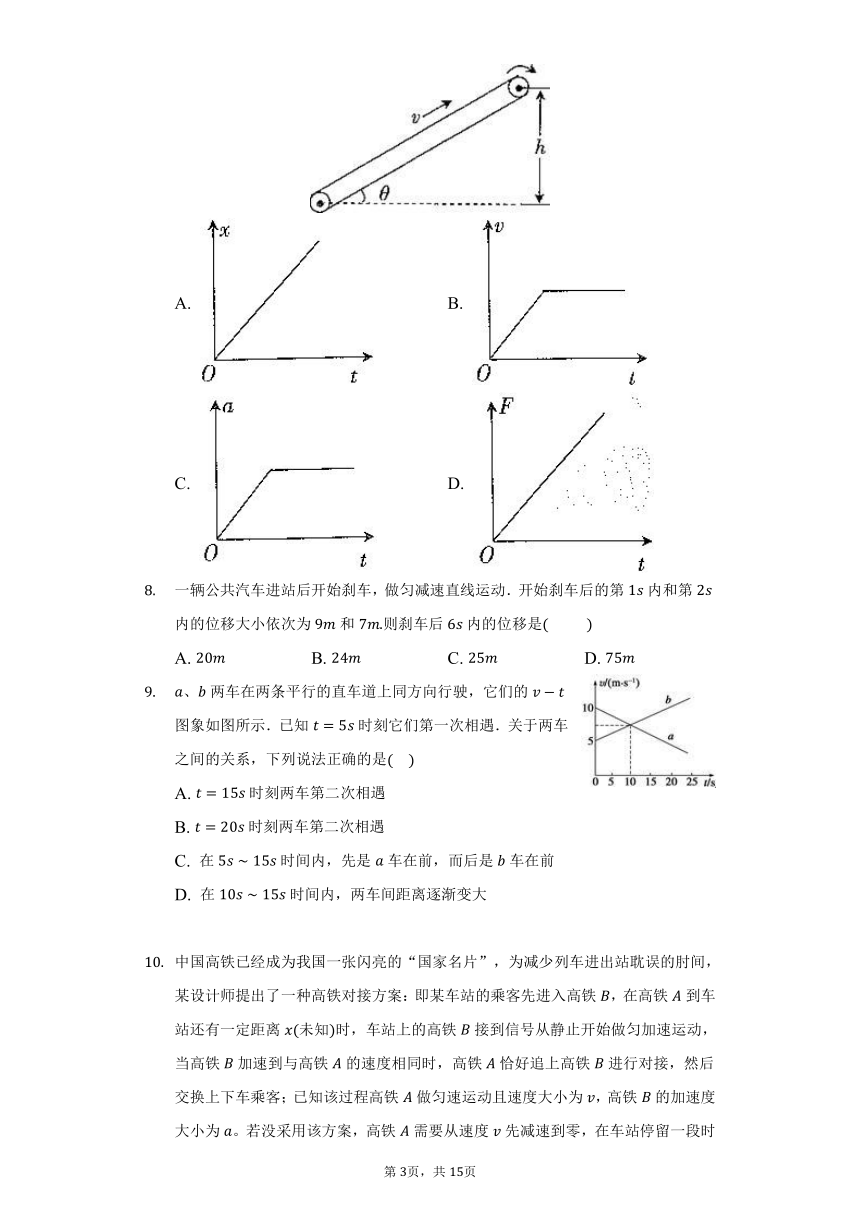
如图所示,传送带与水平面间的夹角,在电动机的带动下始终保持的速率沿顺时针方向运行。现把一工件可视为质点轻轻放在传送带的底端,工件被传送到的高度处。已知工件与传送带间的动摩擦因数,重力加速度,则工件在传送带上运动的整个过程中,其位移、速度、加速度、所受合力随时间变化的图象正确的是
A. B.
C. D.
一辆公共汽车进站后开始刹车,做匀减速直线运动.开始刹车后的第内和第内的位移大小依次为和则刹车后内的位移是
A. B. C. D.
、两车在两条平行的直车道上同方向行驶,它们的图象如图所示.已知时刻它们第一次相遇.关于两车之间的关系,下列说法正确的是
A. 时刻两车第二次相遇
B. 时刻两车第二次相遇
C. 在时间内,先是车在前,而后是车在前
D. 在时间内,两车间距离逐渐变大
中国高铁已经成为我国一张闪亮的“国家名片”,为减少列车进出站耽误的肘间,某设计师提出了一种高铁对接方案:即某车站的乘客先进入高铁,在高铁到车站还有一定距离未知时,车站上的高铁接到信号从静止开始做匀加速运动,当高铁加速到与高铁的速度相同时,高铁恰好追上高铁进行对接,然后交换上下车乘客;已知该过程高铁做匀速运动且速度大小为,高铁的加速度大小为。若没采用该方案,高铁需要从速度先减速到零,在车站停留一段时间,再加速到与原来相同的速度,此时高铁进站和出站的加速度大小都为。如果将高铁视为质点,则下列说法正确的是
A.
B.
C. 利用高铁对接方案每站节约的时间为
D. 利用高铁对接方案每站节约的时间为
二、填空题
I.一物体沿正东方向以的速度匀速运动,又以的速度向北匀速运动,则这内物体的平均速度的大小是________,平均速率的大小是________。如图所示,Ⅰ和Ⅱ分别是甲乙两物体的图象,则甲物体的速度_____,乙物体的速度________,在时,甲、乙两物体相距________。
一滑块由静止开始,从斜面顶端匀加速下滑,第末的速度是求:
前内的位移为____________;
第内的位移为_____________。
小球自某一高度自由落下,它落地时的速度与落到一半高度时的速度之比是__________
如图,两光滑斜面在处连接,小球由处静止释放,经过、两点时速度大小分别为和,设球经过点前后的速度大小不变,则球在、段的加速度大小之比为________,球由运动到的过程中平均速率为________.
一个物体从点由静止开始以加速度做匀加速直线运动,经过时间后到达点,此时将物体的加速度反向,加速度的大小从换为,再经过时间后物体又回到了点,则与的大小之比为:________
三、实验题
打点计时器接在的交流电源上时,每隔______打一个点.做匀变速直线运动的小车拖动纸带穿过打点计时器,纸带上记录的点如图,、、、、为个计数点,相邻两计数点间有个点没标出.已知纸带与点相近的一端跟小车相连,由此可知,小车的加速度大小为_______结果保留三位有效数字,方向与小车运动方向________填“相同”或“相反”;打下点时,小车的瞬时速度为_______计算结果保留三位有效数字.
某次实验打点计时器使用的交流电的频率为,纸带的记录如图所示,图中点为纸带的第一个点,接下来的前几个点模糊,因此从点开始每打五个点取一个计数点:
推测纸带的运动是加速运动还是减速运动?
________________________________________________________________________.
在打出、这两点的时间间隔中,纸带运动的平均速度是________.
点的瞬时速度为________.
答案和解析
1.【答案】
【解析】
【分析】
本题考查了匀变速直线运动的图像;本题的关键要写出解析式,采用比对的方法求出加速度和初速度,明了物体的运动情况后,再由运动学公式研究图象的信息。
【解答】
由图得:;根据匀变速运动的位移公式,得:,则质点的加速度为,初速度为,则知质点的加速度不变,做匀加速直线运动,故AB错误;
质点做匀加速直线运动,在末速度为:。质点在第内的位移为:,故C错误,D正确。
故选D。
2.【答案】
【解析】
【分析】
汽车刹车做匀减速直线运动,根据位移差公式求出加速度大小,由位移与时间的关系求出初速度,计算出刹车过程持续的时间,由速度和位移的关系求解刹车最后的初速度,结合实际刹车的时间,求刹车内的位移。
【解答】
A.汽车刹车做匀减速直线运动,由得,根据位移与时间的关系,得,故A错误;
B.汽车刹车过程持续的时间,故B错误;
C.刹车最后的末速度为,由得,刹车最后的初速度,故C错误;
D.刹车过程持续,刹车后内的位移即为刹车过程的位移,由得,,故D正确。
故选D。
3.【答案】
【解析】
【分析】根据得到物体的加速度;由位移和时间的关系得到物体的初速度;由速度和时间的关系得到第末的速度,由速度和位移的关系得到,进而得到内的平均速度。
把握匀变速直线运动规律的应用时解题的关键。
【解答】
A.根据得, ,A正确;
B.根据,得,B错误;
第末的速度,则 ,位移内的平均速度大小,、D正确.
4.【答案】
【解析】
【分析】
根据平均速度与中间时刻的速度的关系得到点的速度,根据得到加速度,由速度和时间的关系得到点的速度,由位移时间关系求出、之间的距离。
灵活运用匀变速直线运动规律是解题的关键。
【解答】
设物体通过、所用时间均为,则点的速度为,根据得:,则有:,根据速度位移公式得,、两点之间的距离为 ,故A正确。
5.【答案】
【解析】
【分析】
正确理解匀变速直线运动速度公式和运动特征。
物理公式不同于数学公式,不满足物理情景的公式转换,仅满足数学关系式时并不能满足物理关系,所以在公式判断转换上要根据公式包含的物理情景一起分析。
【解答】
A.物体做匀变速直线运动,加速度保持不变,根据,其为加速度的定义式,不能说加速度的大小与物体运动的速度改变量成正比,与速度改变量所对应的时间成反比,故A错误;
B.物体做匀变速直线运动,加速度保持不变,故B错误;
C.因为匀变速直线运动的加速度保持不变,故根据可知,做初速度为零的匀变速直线运动的物体,其位移的大小与物体运动的时间的平方成正比正确;
D.物体做加速运动还是减速运动根据物体运动的速度方向与加速度方向是否相同决定,同向为加速反向为减速,由公式可知,做匀变速直线运动的物体,取初速度方向为正方向,则若加速度,则物体做加速运动,若加速度,则物体做减速运动;因本题中没有注明速度方向为正,仅根据加速度的方向判断加速还是减速是错误的。
故选C。
6.【答案】
【解析】
【分析】
本题考查了匀变速直线运动的速度与时间的关系、匀变速直线运动的位移与时间的关系、平均速度和中间时刻速度公式、位移差公式的相关知识,试题难度一般
【解答】
A.根据可得物体的加速度,A错误;
B.第末的速度,B正确;
C.第内的位移,C错误;
D.物体在前内的位移,则物体在前内的平均速度,D错误.
7.【答案】
【解析】
【分析】
本题的关键是要正确分析工件的受力情况,来判断运动情况,由牛顿第二定律和运动学公式结合分析。分析工件的受力情况,物体受到重力、支持力、和沿斜面向上的摩擦力作用,合力沿斜面向上,物体加速运动,由牛顿第二定律求出加速度。由速度公式求出速度达到与传送带相同的时间,并求出物体通过的位移。当物体与传送带共速时,分析下滑力与最大静摩擦力的关系,判断物体的运动情况,再分析图象的形状。
【解答】
A.在匀加速阶段,由,知图象为抛物线,故A错误;
B.对工件,据牛顿第二定律得:得:,工件速度由加速到所用的时间,在这段时间内工件的位移,传送带的长度,说明物体与传送带共速时还没有到达顶端。因为,所以共速后物体随传送带匀速运动,因此工作先做初速度为零的匀加速直线运动,后做匀速直线运动,故B正确;
C.加速度先不变后为零,故C错误;
D.合外力先不变后为零,故D错误。
故选B。
8.【答案】
【解析】
【分析】
本题是刹车问题,主要考查匀变速直线运动规律的综合运用。开始刹车后的第内和第内位移大小依次为和,根据匀减速直线运动的位移时间公式列出两个方程,求出初速度和加速度.但刹车问题要注意刹车的时间,然后把所给的时间跟刹车时间进行比较,如果所给时间小于刹车时间,则公式里的时间就用所给时间,若所给时间大于刹车时间,说明在此时间之前车已经静止,那只能用刹车时间进行计算。
【解答】
设汽车的初速度为,加速度为根据匀变速直线运动的推论有,得
第内的位移:,代入数据解得:
汽车从刹车到停止所需的时间:
则汽车刹车后内的位移等于内的位移:,故C正确。
故选C。
9.【答案】
【解析】
【分析】
由图象可知做匀减速运动,做匀加速运动,相遇说明在同一时刻两车在同一位置.根据图象与坐标轴围成的面积表示运动的位移,分析两车各个时刻的位置情况即可求解。
本题要能根据图象去分析物体的运动过程,关键要抓住图线和时间轴围成的面积表示物体通过的位移,根据速度的大小关系,分析两车间距的变化,知道速度相等时,间距最大。
【解答】
由图可知,做匀减速运动,做匀加速运动;由题意时两物体相遇,说明开始时在后面,时两物体的位置相同;到内车速度仍大于车,故在前;时间内,的速度大于的速度,但由于开始时落在了的后面,故还将在的后面,时追上了故时两物体再次相遇;故 A正确,BC错误;
D.时刻两车第一次相遇,在的时间内,的速度大于的速度,两车间距逐渐变小,故D错误。
故选A。
10.【答案】
【解析】
【分析】
根据速度时间公式求出高铁加速到高铁的速度相同所用的时间,根据匀速运动求出高铁和运动的位移,根据位移关系求出高铁距离车站的位移;
根据速度位移公式求出运动的位移,再根据速度时间公式求出两段距离高铁运动的时间,如果这段距离高铁不减速求出对应的时间,即可求出利用高铁对接方案每站节约的时间。
本题主要考查了运动学的应用,难度一般,基础题。
【解答】
高铁加速到高铁的速度相同所用的时间,时间内高铁运动的位移,高铁运动的位移,高铁距离车站,故AB错误;
由得高铁减速和加速运动的位移相同,为,这两段距离高铁运动的时间,而如果这段距离高铁不减速,高铁运动的时间,利用高铁对接方案节约时间,故C错误,D正确。
故选D。
11.【答案】I、;;
、;;;
、;
、。
【解析】
【分析】
求出内的位移,根据平均速度等于位移与时间的比值求解平均速度,根据平均速率等于路程与时间的比值求解平均速率。
本题要理解平均速度和平均速率的区别,平均速度等于位移与时间的比值,平均速率等于路程与时间的比值。
【解答】
向东的位移
向北的位移
内的总位移
所以内物体的平均速度的大小
内的总路程
内物体的平均速率
故答案为:;;
【分析】
在位移时间图象中,倾斜的直线表示物体做匀速直线运动,斜率表示速度。
本题关键要掌握两种图象斜率的意义,要能根据形状判断物体的运动性质,读出有用信息,注意位移时间图象和速度时间图象的区别,不能张冠李戴。
【解答】
在位移时间图象中,图线的斜率表示速度
则甲物体的速度
乙物体的速度
在时,甲、乙两物体相距
故答案为:;;;
【分析】
根据速度公式求解加速度,根据位移公式求解位移。
本题关键掌握匀变速直线运动的运动公式,灵活选择公式求解,注意明确前、第所指的时间段。
【解答】
滑块的加速度
前内的位移
前内的位移
前内的位移
所以第内的位移为
故答案为:;;
【分析】
小球自由下落,做自由落体运动,自由落体运动是初速度为零、加速度为的匀加速直线运动,根据位移速度关系式分析求解。
本题关键知道自由落体运动的规律。
【解答】
设自由下落的高度为,落地速度为,落到高度一半时的速度为
根据位移速度关系式有:,得
,得
所以
故答案为:。
12.【答案】;
【解析】
【分析】本题考查了匀变速直线运动的速度与位移的关系、平均速度和中间时刻速度公式的相关知识,试题难度一般。
根据速度位移关系求出加速度的大小,即可求出加速度大小的比值;结合平均速度的推论公式即可分析。
【解答】小球在段和段均做匀加速直线运动,根据,可得两个过程中加速度大小分别为,,可得加速度大小之比设两个阶段的路程均为,则有,,可得从运动到的过程中平均速率.
13.【答案】:
【解析】
【分析】
根据速度公式求出加速速度,根据位移公式求出加速与减速位移;结合题设即可求出。
熟悉匀变速直线运动规律是解题的关键。
【解答】
匀加速过程的末速度
匀加速的位移
匀减速过程返回:
由题有:
联立式,可解得:::
14.【答案】;;相反;
【解析】
【分析】
要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用,要注意单位的换算,及有效数字的保留。
根据匀变速直线运动的推论公式可以求出加速度的大小,根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出纸带上到的时间中点的速度大小,然后根据可以求出打下点时小车的瞬时速度大小。
【解答】
解:每相邻两个计数点之间都有个点未画出,因此计数点之间的时间为;
根据运动学公式推论采用逐差法得出:
;
方向与小车运动方向相反;
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,
有到点时间中点的速度为:
从计数点“”到“”的时间中点到“”的时间为:,根据公式得,点的速度为:
。
故答案为:;;相反;。
15.【答案】 加速运动
【解析】
【分析】本题主要考察用打点计时器测速度,通过计算得出物体速度和加速度。
知道相邻的计数点之间的时间间隔相等,根据纸带上相邻点的距离间隔判断小车的运动情况。
应用平均速度公式求出平均速度。
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上时小车的瞬时速度大小。
【解答】
从点开始相邻计数点间的时间间隔为,每隔纸带运动的位移分别是、、、、,间距逐渐增加,说明纸带做加速运动。
、间纸带运动的平均速度为 .
点的瞬时速度可以用段的平均速度表示,故 .
第2页,共2页
第1页,共1页
一、单选题
一质点沿轴正方向做直线运动,通过坐标原点时开始计时,图像如图,则
A. 质点做匀速直线运动,速度为
B. 质点做匀加速直线运动,加速度为
C. 质点在末速度为
D. 质点在第内的位移为
一辆汽车遇到前方有障碍物开始刹车,刹车后的第内和第内位移大小依次为和。则下列分析正确的是
A. 汽车开始刹车时的初速度为
B. 刹车过程持续的时间为
C. 刹车最后的初速度为
D. 刹车后内的位移是
物体以初速度做匀减速直线运动,第内通过的位移为,第内通过的位移为,又经过位移物体的速度减小为,则下列说法中不正确的是
A. 加速度的大小为
B. 初速度的大小为
C. 位移的大小为
D. 位移内的平均速度大小为
如图所示,物体从点由静止开始做匀加速直线运动,途经、、三点,其中,。若物体通过和这两段位移的时间相等,则、两点之间的距离等于
A. B. C. D.
关于匀变速直线运动的公式,有下面几种说法,正确的是
A. 由公式可知,做匀变速直线运动的物体,其加速度的大小与物体运动的速度改变量成正比,与速度改变量所对应的时间成反比
B. 由公式可知,做匀变速直线运动的物体,其加速度的大小与物体运动的速度平方的改变量成正比,与物体运动的位移成反比
C. 由公式可知,做初速度为零的匀变速直线运动的物体,其位移的大小与物体运动的时间的平方成正比
D. 由公式可知,做匀变速直线运动的物体,若加速度,则物体做加速运动,若加速度,则物体做减速运动
物体从静止开始做匀加速直线运动,已知第内与第内的位移之差是,则可知
A. 物体运动的加速度大小为
B. 第末的速度大小为
C. 第内的位移大小为
D. 物体在前内的平均速度大小为
如图所示,传送带与水平面间的夹角,在电动机的带动下始终保持的速率沿顺时针方向运行。现把一工件可视为质点轻轻放在传送带的底端,工件被传送到的高度处。已知工件与传送带间的动摩擦因数,重力加速度,则工件在传送带上运动的整个过程中,其位移、速度、加速度、所受合力随时间变化的图象正确的是
A. B.
C. D.
一辆公共汽车进站后开始刹车,做匀减速直线运动.开始刹车后的第内和第内的位移大小依次为和则刹车后内的位移是
A. B. C. D.
、两车在两条平行的直车道上同方向行驶,它们的图象如图所示.已知时刻它们第一次相遇.关于两车之间的关系,下列说法正确的是
A. 时刻两车第二次相遇
B. 时刻两车第二次相遇
C. 在时间内,先是车在前,而后是车在前
D. 在时间内,两车间距离逐渐变大
中国高铁已经成为我国一张闪亮的“国家名片”,为减少列车进出站耽误的肘间,某设计师提出了一种高铁对接方案:即某车站的乘客先进入高铁,在高铁到车站还有一定距离未知时,车站上的高铁接到信号从静止开始做匀加速运动,当高铁加速到与高铁的速度相同时,高铁恰好追上高铁进行对接,然后交换上下车乘客;已知该过程高铁做匀速运动且速度大小为,高铁的加速度大小为。若没采用该方案,高铁需要从速度先减速到零,在车站停留一段时间,再加速到与原来相同的速度,此时高铁进站和出站的加速度大小都为。如果将高铁视为质点,则下列说法正确的是
A.
B.
C. 利用高铁对接方案每站节约的时间为
D. 利用高铁对接方案每站节约的时间为
二、填空题
I.一物体沿正东方向以的速度匀速运动,又以的速度向北匀速运动,则这内物体的平均速度的大小是________,平均速率的大小是________。如图所示,Ⅰ和Ⅱ分别是甲乙两物体的图象,则甲物体的速度_____,乙物体的速度________,在时,甲、乙两物体相距________。
一滑块由静止开始,从斜面顶端匀加速下滑,第末的速度是求:
前内的位移为____________;
第内的位移为_____________。
小球自某一高度自由落下,它落地时的速度与落到一半高度时的速度之比是__________
如图,两光滑斜面在处连接,小球由处静止释放,经过、两点时速度大小分别为和,设球经过点前后的速度大小不变,则球在、段的加速度大小之比为________,球由运动到的过程中平均速率为________.
一个物体从点由静止开始以加速度做匀加速直线运动,经过时间后到达点,此时将物体的加速度反向,加速度的大小从换为,再经过时间后物体又回到了点,则与的大小之比为:________
三、实验题
打点计时器接在的交流电源上时,每隔______打一个点.做匀变速直线运动的小车拖动纸带穿过打点计时器,纸带上记录的点如图,、、、、为个计数点,相邻两计数点间有个点没标出.已知纸带与点相近的一端跟小车相连,由此可知,小车的加速度大小为_______结果保留三位有效数字,方向与小车运动方向________填“相同”或“相反”;打下点时,小车的瞬时速度为_______计算结果保留三位有效数字.
某次实验打点计时器使用的交流电的频率为,纸带的记录如图所示,图中点为纸带的第一个点,接下来的前几个点模糊,因此从点开始每打五个点取一个计数点:
推测纸带的运动是加速运动还是减速运动?
________________________________________________________________________.
在打出、这两点的时间间隔中,纸带运动的平均速度是________.
点的瞬时速度为________.
答案和解析
1.【答案】
【解析】
【分析】
本题考查了匀变速直线运动的图像;本题的关键要写出解析式,采用比对的方法求出加速度和初速度,明了物体的运动情况后,再由运动学公式研究图象的信息。
【解答】
由图得:;根据匀变速运动的位移公式,得:,则质点的加速度为,初速度为,则知质点的加速度不变,做匀加速直线运动,故AB错误;
质点做匀加速直线运动,在末速度为:。质点在第内的位移为:,故C错误,D正确。
故选D。
2.【答案】
【解析】
【分析】
汽车刹车做匀减速直线运动,根据位移差公式求出加速度大小,由位移与时间的关系求出初速度,计算出刹车过程持续的时间,由速度和位移的关系求解刹车最后的初速度,结合实际刹车的时间,求刹车内的位移。
【解答】
A.汽车刹车做匀减速直线运动,由得,根据位移与时间的关系,得,故A错误;
B.汽车刹车过程持续的时间,故B错误;
C.刹车最后的末速度为,由得,刹车最后的初速度,故C错误;
D.刹车过程持续,刹车后内的位移即为刹车过程的位移,由得,,故D正确。
故选D。
3.【答案】
【解析】
【分析】根据得到物体的加速度;由位移和时间的关系得到物体的初速度;由速度和时间的关系得到第末的速度,由速度和位移的关系得到,进而得到内的平均速度。
把握匀变速直线运动规律的应用时解题的关键。
【解答】
A.根据得, ,A正确;
B.根据,得,B错误;
第末的速度,则 ,位移内的平均速度大小,、D正确.
4.【答案】
【解析】
【分析】
根据平均速度与中间时刻的速度的关系得到点的速度,根据得到加速度,由速度和时间的关系得到点的速度,由位移时间关系求出、之间的距离。
灵活运用匀变速直线运动规律是解题的关键。
【解答】
设物体通过、所用时间均为,则点的速度为,根据得:,则有:,根据速度位移公式得,、两点之间的距离为 ,故A正确。
5.【答案】
【解析】
【分析】
正确理解匀变速直线运动速度公式和运动特征。
物理公式不同于数学公式,不满足物理情景的公式转换,仅满足数学关系式时并不能满足物理关系,所以在公式判断转换上要根据公式包含的物理情景一起分析。
【解答】
A.物体做匀变速直线运动,加速度保持不变,根据,其为加速度的定义式,不能说加速度的大小与物体运动的速度改变量成正比,与速度改变量所对应的时间成反比,故A错误;
B.物体做匀变速直线运动,加速度保持不变,故B错误;
C.因为匀变速直线运动的加速度保持不变,故根据可知,做初速度为零的匀变速直线运动的物体,其位移的大小与物体运动的时间的平方成正比正确;
D.物体做加速运动还是减速运动根据物体运动的速度方向与加速度方向是否相同决定,同向为加速反向为减速,由公式可知,做匀变速直线运动的物体,取初速度方向为正方向,则若加速度,则物体做加速运动,若加速度,则物体做减速运动;因本题中没有注明速度方向为正,仅根据加速度的方向判断加速还是减速是错误的。
故选C。
6.【答案】
【解析】
【分析】
本题考查了匀变速直线运动的速度与时间的关系、匀变速直线运动的位移与时间的关系、平均速度和中间时刻速度公式、位移差公式的相关知识,试题难度一般
【解答】
A.根据可得物体的加速度,A错误;
B.第末的速度,B正确;
C.第内的位移,C错误;
D.物体在前内的位移,则物体在前内的平均速度,D错误.
7.【答案】
【解析】
【分析】
本题的关键是要正确分析工件的受力情况,来判断运动情况,由牛顿第二定律和运动学公式结合分析。分析工件的受力情况,物体受到重力、支持力、和沿斜面向上的摩擦力作用,合力沿斜面向上,物体加速运动,由牛顿第二定律求出加速度。由速度公式求出速度达到与传送带相同的时间,并求出物体通过的位移。当物体与传送带共速时,分析下滑力与最大静摩擦力的关系,判断物体的运动情况,再分析图象的形状。
【解答】
A.在匀加速阶段,由,知图象为抛物线,故A错误;
B.对工件,据牛顿第二定律得:得:,工件速度由加速到所用的时间,在这段时间内工件的位移,传送带的长度,说明物体与传送带共速时还没有到达顶端。因为,所以共速后物体随传送带匀速运动,因此工作先做初速度为零的匀加速直线运动,后做匀速直线运动,故B正确;
C.加速度先不变后为零,故C错误;
D.合外力先不变后为零,故D错误。
故选B。
8.【答案】
【解析】
【分析】
本题是刹车问题,主要考查匀变速直线运动规律的综合运用。开始刹车后的第内和第内位移大小依次为和,根据匀减速直线运动的位移时间公式列出两个方程,求出初速度和加速度.但刹车问题要注意刹车的时间,然后把所给的时间跟刹车时间进行比较,如果所给时间小于刹车时间,则公式里的时间就用所给时间,若所给时间大于刹车时间,说明在此时间之前车已经静止,那只能用刹车时间进行计算。
【解答】
设汽车的初速度为,加速度为根据匀变速直线运动的推论有,得
第内的位移:,代入数据解得:
汽车从刹车到停止所需的时间:
则汽车刹车后内的位移等于内的位移:,故C正确。
故选C。
9.【答案】
【解析】
【分析】
由图象可知做匀减速运动,做匀加速运动,相遇说明在同一时刻两车在同一位置.根据图象与坐标轴围成的面积表示运动的位移,分析两车各个时刻的位置情况即可求解。
本题要能根据图象去分析物体的运动过程,关键要抓住图线和时间轴围成的面积表示物体通过的位移,根据速度的大小关系,分析两车间距的变化,知道速度相等时,间距最大。
【解答】
由图可知,做匀减速运动,做匀加速运动;由题意时两物体相遇,说明开始时在后面,时两物体的位置相同;到内车速度仍大于车,故在前;时间内,的速度大于的速度,但由于开始时落在了的后面,故还将在的后面,时追上了故时两物体再次相遇;故 A正确,BC错误;
D.时刻两车第一次相遇,在的时间内,的速度大于的速度,两车间距逐渐变小,故D错误。
故选A。
10.【答案】
【解析】
【分析】
根据速度时间公式求出高铁加速到高铁的速度相同所用的时间,根据匀速运动求出高铁和运动的位移,根据位移关系求出高铁距离车站的位移;
根据速度位移公式求出运动的位移,再根据速度时间公式求出两段距离高铁运动的时间,如果这段距离高铁不减速求出对应的时间,即可求出利用高铁对接方案每站节约的时间。
本题主要考查了运动学的应用,难度一般,基础题。
【解答】
高铁加速到高铁的速度相同所用的时间,时间内高铁运动的位移,高铁运动的位移,高铁距离车站,故AB错误;
由得高铁减速和加速运动的位移相同,为,这两段距离高铁运动的时间,而如果这段距离高铁不减速,高铁运动的时间,利用高铁对接方案节约时间,故C错误,D正确。
故选D。
11.【答案】I、;;
、;;;
、;
、。
【解析】
【分析】
求出内的位移,根据平均速度等于位移与时间的比值求解平均速度,根据平均速率等于路程与时间的比值求解平均速率。
本题要理解平均速度和平均速率的区别,平均速度等于位移与时间的比值,平均速率等于路程与时间的比值。
【解答】
向东的位移
向北的位移
内的总位移
所以内物体的平均速度的大小
内的总路程
内物体的平均速率
故答案为:;;
【分析】
在位移时间图象中,倾斜的直线表示物体做匀速直线运动,斜率表示速度。
本题关键要掌握两种图象斜率的意义,要能根据形状判断物体的运动性质,读出有用信息,注意位移时间图象和速度时间图象的区别,不能张冠李戴。
【解答】
在位移时间图象中,图线的斜率表示速度
则甲物体的速度
乙物体的速度
在时,甲、乙两物体相距
故答案为:;;;
【分析】
根据速度公式求解加速度,根据位移公式求解位移。
本题关键掌握匀变速直线运动的运动公式,灵活选择公式求解,注意明确前、第所指的时间段。
【解答】
滑块的加速度
前内的位移
前内的位移
前内的位移
所以第内的位移为
故答案为:;;
【分析】
小球自由下落,做自由落体运动,自由落体运动是初速度为零、加速度为的匀加速直线运动,根据位移速度关系式分析求解。
本题关键知道自由落体运动的规律。
【解答】
设自由下落的高度为,落地速度为,落到高度一半时的速度为
根据位移速度关系式有:,得
,得
所以
故答案为:。
12.【答案】;
【解析】
【分析】本题考查了匀变速直线运动的速度与位移的关系、平均速度和中间时刻速度公式的相关知识,试题难度一般。
根据速度位移关系求出加速度的大小,即可求出加速度大小的比值;结合平均速度的推论公式即可分析。
【解答】小球在段和段均做匀加速直线运动,根据,可得两个过程中加速度大小分别为,,可得加速度大小之比设两个阶段的路程均为,则有,,可得从运动到的过程中平均速率.
13.【答案】:
【解析】
【分析】
根据速度公式求出加速速度,根据位移公式求出加速与减速位移;结合题设即可求出。
熟悉匀变速直线运动规律是解题的关键。
【解答】
匀加速过程的末速度
匀加速的位移
匀减速过程返回:
由题有:
联立式,可解得:::
14.【答案】;;相反;
【解析】
【分析】
要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用,要注意单位的换算,及有效数字的保留。
根据匀变速直线运动的推论公式可以求出加速度的大小,根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出纸带上到的时间中点的速度大小,然后根据可以求出打下点时小车的瞬时速度大小。
【解答】
解:每相邻两个计数点之间都有个点未画出,因此计数点之间的时间为;
根据运动学公式推论采用逐差法得出:
;
方向与小车运动方向相反;
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,
有到点时间中点的速度为:
从计数点“”到“”的时间中点到“”的时间为:,根据公式得,点的速度为:
。
故答案为:;;相反;。
15.【答案】 加速运动
【解析】
【分析】本题主要考察用打点计时器测速度,通过计算得出物体速度和加速度。
知道相邻的计数点之间的时间间隔相等,根据纸带上相邻点的距离间隔判断小车的运动情况。
应用平均速度公式求出平均速度。
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上时小车的瞬时速度大小。
【解答】
从点开始相邻计数点间的时间间隔为,每隔纸带运动的位移分别是、、、、,间距逐渐增加,说明纸带做加速运动。
、间纸带运动的平均速度为 .
点的瞬时速度可以用段的平均速度表示,故 .
第2页,共2页
第1页,共1页
同课章节目录
- 第1章 绪论
- 物理学与自然规律
- 物理学与社会发展
- 怎样学习物理学
- 高中物理教材特点
- 第2章 运动的描述
- 导入 认识运动
- 第1节 运动、空间和时间
- 第2节 质点和位移
- 第3节 速度和加速度
- 第3章 匀变速直线运动的研究
- 导入 速度的变化
- 第1节 匀变速直线运动的规律
- 第2节 匀变速直线运动的实验探究
- 第3节 匀变速直线运动实例-自由落体运动
- 第4章 相互作用
- 导入 奇特的力现象
- 第1节 重力与重心
- 第2节 形变与弹力
- 第3节 摩擦力
- 第5章 力与平衡
- 导入 感悟平衡之美
- 第1节 力的合成
- 第2节 力的分解
- 第3节 力的平衡
- 第4节 平衡条件的应用
- 第6章 力与运动
- 导入 跨越时空的对话
- 第1节 牛顿第一定律
- 第2节 牛顿第二定律
- 第3节 牛顿第三定律
- 第4节 超重与失重
- 本章复习与测试
