人教版八年级上册数学 13.4最短路径问题 专题训练(word版含答案)
文档属性
| 名称 | 人教版八年级上册数学 13.4最短路径问题 专题训练(word版含答案) | 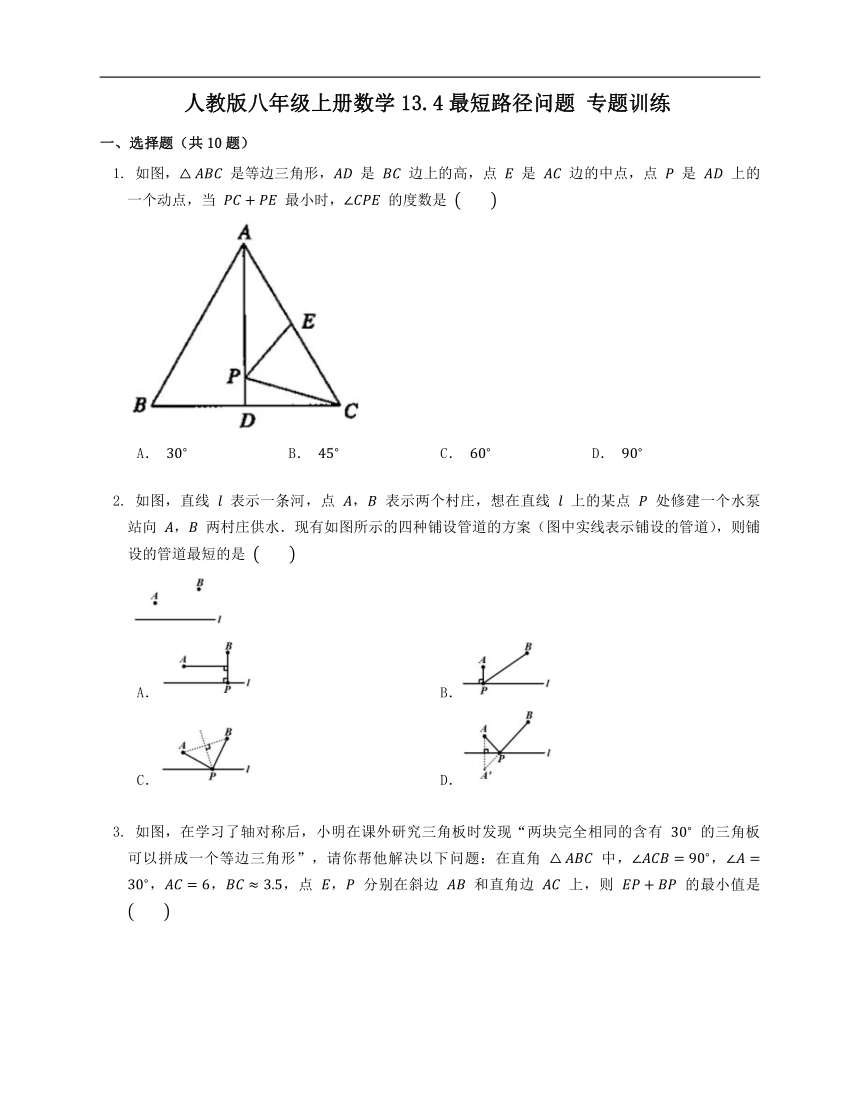 | |
| 格式 | zip | ||
| 文件大小 | 240.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-13 22:20:09 | ||
图片预览



文档简介
人教版八年级上册数学13.4最短路径问题 专题训练
一、选择题(共10题)
如图, 是等边三角形, 是 边上的高,点 是 边的中点,点 是 上的一个动点,当 最小时, 的度数是
A. B. C. D.
如图,直线 表示一条河,点 , 表示两个村庄,想在直线 上的某点 处修建一个水泵站向 , 两村庄供水.现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设的管道最短的是
A. B.
C. D.
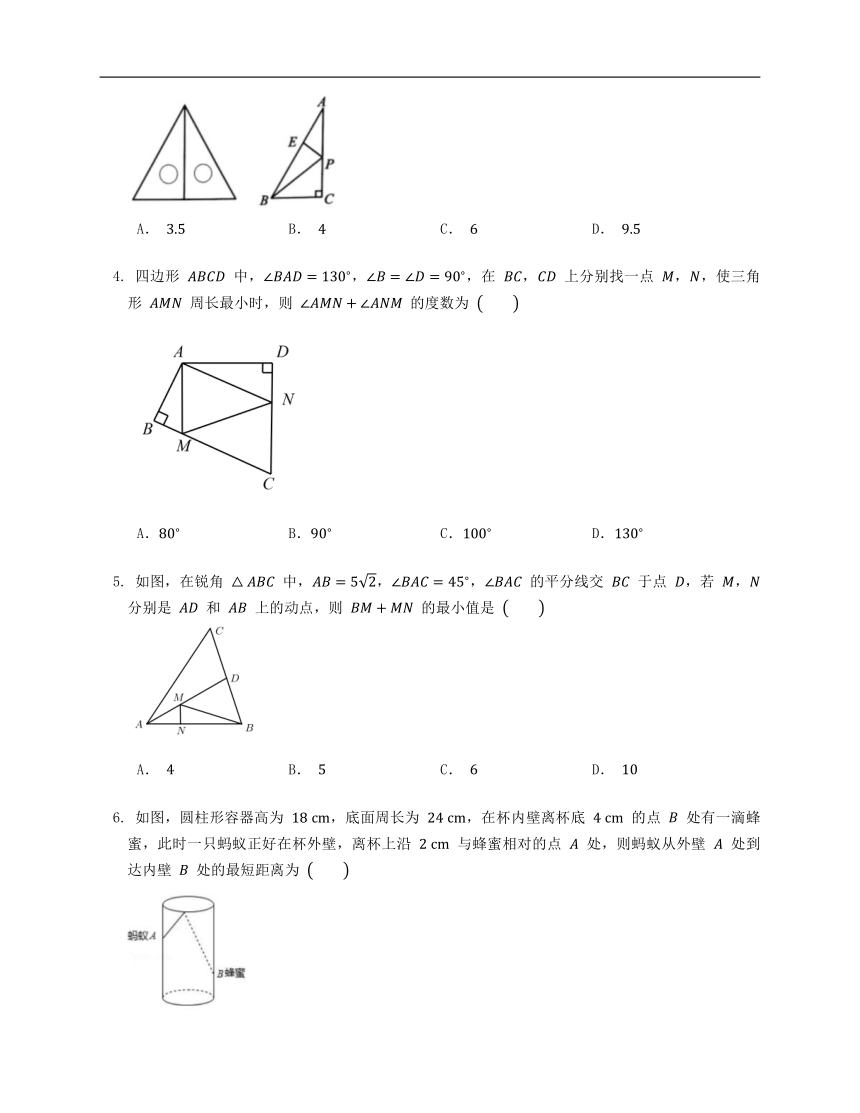
如图,在学习了轴对称后,小明在课外研究三角板时发现“两块完全相同的含有 的三角板可以拼成一个等边三角形”,请你帮他解决以下问题:在直角 中,,,,,点 , 分别在斜边 和直角边 上,则 的最小值是
A. B. C. D.
四边形 中,,,在 , 上分别找一点 ,,使三角形 周长最小时,则 的度数为
A. B. C. D.
如图,在锐角 中,,, 的平分线交 于点 ,若 , 分别是 和 上的动点,则 的最小值是
A. B. C. D.
如图,圆柱形容器高为 ,底面周长为 ,在杯内壁离杯底 的点 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿 与蜂蜜相对的点 处,则蚂蚁从外壁 处到达内壁 处的最短距离为
A. B. C. D.
如图,点 是 内任意一点,且 ,点 和点 分别是射线 和射线 上的动点,当 周长取最小值时,则 的度数为
A. B. C. D.
如图,已知 的大小为 , 是 内部的一个定点,且 ,点 , 分别是 , 上的动点,若 周长的最小值等于 ,则
A. B. C. D.
如图,点 为 内一点,分别作点 关于 , 的对称点 ,,连接 , 交 于 ,交 于 ,若 ,则 周长为
A. B. C. D.
如图,在直角坐标系中,点 , 的坐标分别为 和 ,点 是 轴上的一个动点,且 ,, 三点不在同一条直线上,当 的周长最小时,点 的坐标是
A. B. C. D.
二、填空题(共8题)
如图,等腰三角形 的底边 长为 ,面积是 ,腰 的垂直平分线 分别交 , 边于 , 点,若点 为 边的中点,点 为线段 上一动点,则 周长的最小值为 .
如图,在四边形 中,,,在边 , 上分别找一点 ,,使 的周长最小,此时 .
已知,等腰 中,, 是高 上任一点, 是腰 上任一点,腰 ,,,那么线段 的最小值是 .
如图,若 , 为 内一定点, 上有一个点 , 上有一个点 ,当 的周长取最小值时,则 的度数是 .
如图,等边 的周长为 , 为 边上的中线,动点 , 分别在线段 , 上运动,连接 ,,当 长为 时,线段 的和为最小.
如图,在 中,,, 的垂直平分线交 于点 ,交 于点 ,在直线 上存在一点 ,使 ,, 三点构成的 的周长最小,则 的周长最小值为 .
如图,在河流的同岸有 , 两个村庄,要在河岸 上确定相距 米的两点 ,(点 在点 的右边),使得 的和最小.用作图的方式来确定点 ,并说明确定点 的步骤是 .
如图,在 中,,,,.点 是 上一动点,则 的最小值为 .
三、解答题(共4题)
如图,已知 ,,.
(1) 在图中画出 关于 轴对称的 .
(2) 的面积 ; 边上的高 .
(3) 在 轴上有一点 ,使 最小,此时 的最小值 .
尺规作图:在直线 上作出一点 ,使 最短,要求:不写作法,保留作图痕迹,标注点 .
已知 和 , 两点,求作一点 ,使 到 两边的距离相等,且使点 到 , 两点的距离和最小.
(1) 保留作图痕迹.
(2) 写出每步作图的依据.
已知 与 关于 轴对称,点 ,, 的对称点分别是 ,,.
(1) 在图中画出 ;
(2) 写出点 ,, 的坐标;
(3) 在 轴上有一点 ,且 的值最小,画出点 ,并保留作图痕迹.
答案
一、选择题(共10题)
1. 【答案】C
2. 【答案】D
3. 【答案】C
4. 【答案】C
5. 【答案】B
6. 【答案】D
7. 【答案】B
8. 【答案】A
9. 【答案】C
10. 【答案】D
二、填空题(共8题)
11. 【答案】
12. 【答案】
13. 【答案】
14. 【答案】
15. 【答案】
16. 【答案】
17. 【答案】如图:点 即为所求.
①如图,作 ,且 .
②过 向 垂线交于点 并延长,使 ,
③连接 ,交点为点 .
④点 向左作 ,,则点 确定.
18. 【答案】
三、解答题(共4题)
19. 【答案】
(1) 所作图形如下图所示:
(2) ;
(3)
20. 【答案】如图,点 为所作.
21. 【答案】
(1)
(2) ①作 的平分线 ,
②作 关于 的对称点 ,
③连接 交 于 ,点 为所求作的点.
22. 【答案】
(1) 如图所示, 即为所求.
(2) 点 ,, 的坐标分别为 ,,.
(3) 如图所示,连接 ,交 轴于 ,连接 ,则 ,
故 的最小值等于 的长,
点 即为所求.
一、选择题(共10题)
如图, 是等边三角形, 是 边上的高,点 是 边的中点,点 是 上的一个动点,当 最小时, 的度数是
A. B. C. D.
如图,直线 表示一条河,点 , 表示两个村庄,想在直线 上的某点 处修建一个水泵站向 , 两村庄供水.现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设的管道最短的是
A. B.
C. D.
如图,在学习了轴对称后,小明在课外研究三角板时发现“两块完全相同的含有 的三角板可以拼成一个等边三角形”,请你帮他解决以下问题:在直角 中,,,,,点 , 分别在斜边 和直角边 上,则 的最小值是
A. B. C. D.
四边形 中,,,在 , 上分别找一点 ,,使三角形 周长最小时,则 的度数为
A. B. C. D.
如图,在锐角 中,,, 的平分线交 于点 ,若 , 分别是 和 上的动点,则 的最小值是
A. B. C. D.
如图,圆柱形容器高为 ,底面周长为 ,在杯内壁离杯底 的点 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿 与蜂蜜相对的点 处,则蚂蚁从外壁 处到达内壁 处的最短距离为
A. B. C. D.
如图,点 是 内任意一点,且 ,点 和点 分别是射线 和射线 上的动点,当 周长取最小值时,则 的度数为
A. B. C. D.
如图,已知 的大小为 , 是 内部的一个定点,且 ,点 , 分别是 , 上的动点,若 周长的最小值等于 ,则
A. B. C. D.
如图,点 为 内一点,分别作点 关于 , 的对称点 ,,连接 , 交 于 ,交 于 ,若 ,则 周长为
A. B. C. D.
如图,在直角坐标系中,点 , 的坐标分别为 和 ,点 是 轴上的一个动点,且 ,, 三点不在同一条直线上,当 的周长最小时,点 的坐标是
A. B. C. D.
二、填空题(共8题)
如图,等腰三角形 的底边 长为 ,面积是 ,腰 的垂直平分线 分别交 , 边于 , 点,若点 为 边的中点,点 为线段 上一动点,则 周长的最小值为 .
如图,在四边形 中,,,在边 , 上分别找一点 ,,使 的周长最小,此时 .
已知,等腰 中,, 是高 上任一点, 是腰 上任一点,腰 ,,,那么线段 的最小值是 .
如图,若 , 为 内一定点, 上有一个点 , 上有一个点 ,当 的周长取最小值时,则 的度数是 .
如图,等边 的周长为 , 为 边上的中线,动点 , 分别在线段 , 上运动,连接 ,,当 长为 时,线段 的和为最小.
如图,在 中,,, 的垂直平分线交 于点 ,交 于点 ,在直线 上存在一点 ,使 ,, 三点构成的 的周长最小,则 的周长最小值为 .
如图,在河流的同岸有 , 两个村庄,要在河岸 上确定相距 米的两点 ,(点 在点 的右边),使得 的和最小.用作图的方式来确定点 ,并说明确定点 的步骤是 .
如图,在 中,,,,.点 是 上一动点,则 的最小值为 .
三、解答题(共4题)
如图,已知 ,,.
(1) 在图中画出 关于 轴对称的 .
(2) 的面积 ; 边上的高 .
(3) 在 轴上有一点 ,使 最小,此时 的最小值 .
尺规作图:在直线 上作出一点 ,使 最短,要求:不写作法,保留作图痕迹,标注点 .
已知 和 , 两点,求作一点 ,使 到 两边的距离相等,且使点 到 , 两点的距离和最小.
(1) 保留作图痕迹.
(2) 写出每步作图的依据.
已知 与 关于 轴对称,点 ,, 的对称点分别是 ,,.
(1) 在图中画出 ;
(2) 写出点 ,, 的坐标;
(3) 在 轴上有一点 ,且 的值最小,画出点 ,并保留作图痕迹.
答案
一、选择题(共10题)
1. 【答案】C
2. 【答案】D
3. 【答案】C
4. 【答案】C
5. 【答案】B
6. 【答案】D
7. 【答案】B
8. 【答案】A
9. 【答案】C
10. 【答案】D
二、填空题(共8题)
11. 【答案】
12. 【答案】
13. 【答案】
14. 【答案】
15. 【答案】
16. 【答案】
17. 【答案】如图:点 即为所求.
①如图,作 ,且 .
②过 向 垂线交于点 并延长,使 ,
③连接 ,交点为点 .
④点 向左作 ,,则点 确定.
18. 【答案】
三、解答题(共4题)
19. 【答案】
(1) 所作图形如下图所示:
(2) ;
(3)
20. 【答案】如图,点 为所作.
21. 【答案】
(1)
(2) ①作 的平分线 ,
②作 关于 的对称点 ,
③连接 交 于 ,点 为所求作的点.
22. 【答案】
(1) 如图所示, 即为所求.
(2) 点 ,, 的坐标分别为 ,,.
(3) 如图所示,连接 ,交 轴于 ,连接 ,则 ,
故 的最小值等于 的长,
点 即为所求.
