2021-2022学年人教版数学九年级上册22.1.2二次函数y=ax?的图象与性质 课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册22.1.2二次函数y=ax?的图象与性质 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 186.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-13 11:04:58 | ||
图片预览





文档简介
(共18张PPT)
21.1.2二次函数 图象和性质
目录
01
教学目标
02
知识点框架
03
例题练习
04
作业布置
教学目标
掌握二次函数 图象和性质并熟练应用
01
知识点框架
02
知识点框架
请各位同学回想一下用什么方法来画函数图象?
。
用描点法画函数图象的步骤:
1.列表
2.描点
3.连线
知识点框架
画二次函数y=x 和y=-x 的图象
列表:
x … -3 -2 -1 0 1 2 3 …
y=x … …
y=-x … …
知识点框架
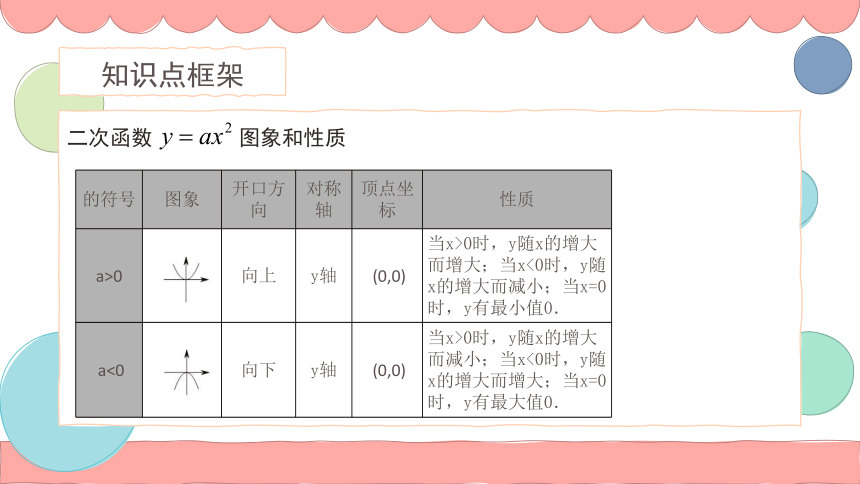
二次函数 图象和性质
的符号 图象 开口方向 对称轴 顶点坐标 性质
a>0 向上 y轴 (0,0) 当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小;当x=0时,y有最小值0.
a<0 向下 y轴 (0,0) 当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大;当x=0时,y有最大值0.
例题练习
03
例题
例1.当ab>0时,y=ax 与y=ax+b的图象大致是( )
例2.二次函数y=(k+1)x2的图象如图,则k的取值范围为________.
例题
例3. 的顶点坐标是( ),对称轴是________,开口向________;
例4.下列各点:(-1,2),(-1,-2),(-2,-4),(-2,4),其中在二次函数y=-2x 的图象上的是____.
例5.抛物线y=2x ,y=-2x ,y= x 的共同性质是( )
A.开口向上 B.对称轴是y轴
C.都有最高点 D.y随x的增大而增大
例题
例6.关于函数y=3x 的性质表述正确的一项是( )
A.无论x为任何实数,y的值总为正
B.当x值增大时,y的值也增大
C.它的图象关于y轴对称
D.它的图象在第一、三象限内
例7.已知点(-1,y ),(2,y ),(-3,y )都在函数y=x 的图象上,则( )
A.yC.y 练习
1.在如图所示网格内建立恰当直角坐标系后,画出函数y=2x 和y=- x 的图象,并根据图象回答下列问题(设小方格的边长为1):
(1)说出这两个函数图象的开口方向,对称轴和顶点坐标;
(2)抛物线y=2x ,当x______时,抛物线上的点都在x轴
的上方,它的顶点是图象的最______点;
(3)函数y=- x ,对于一切x的值,总有函数y______0;
当x______时,y有最______值是______.
练习
2.写出图象经过点(-1,1)的一个二次函数解析式是_____________.
3.已知二次函数y=(m-2)x 的图象开口向下,则m的取值范围是_______
4.下列各点:(-1,2),(-1,-2),(-2,-4),(-2,4),其中在二次函数y=-2x 的图象上的是________________.
5.已知二次函数y=ax 的图象经过点A(-1,- ).
(1)求这个二次函数的解析式并画出其图象;
(2)请说出这个二次函数的顶点坐标、对称轴.
作业布置
04
作业布置
1.已知二次函数y=ax 的图象经过点A(-1,- ).
(1)求这个二次函数的解析式并画出其图象;
(2)请说出这个二次函数的顶点坐标、对称轴.
作业布置
2.下列四个二次函数:①y=x2,②y=-2x2,③y=x2,④y=3x2,其中抛物线开口从大到小的排列顺序是_____________
3.二次函数y=-6x2,当x1>x2>0时,y1与y2的大小关系为____________.
4.分别求出符合下列条件的抛物线y=ax 的解析式:
(1)经过点(-3,2);
(2)与y=x2开口大小相同,方向相反.
作业布置
5.已知二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A、B两点,如图所示,其中A(-1,-1),求△OAB的面积.
下节课见!
21.1.2二次函数 图象和性质
目录
01
教学目标
02
知识点框架
03
例题练习
04
作业布置
教学目标
掌握二次函数 图象和性质并熟练应用
01
知识点框架
02
知识点框架
请各位同学回想一下用什么方法来画函数图象?
。
用描点法画函数图象的步骤:
1.列表
2.描点
3.连线
知识点框架
画二次函数y=x 和y=-x 的图象
列表:
x … -3 -2 -1 0 1 2 3 …
y=x … …
y=-x … …
知识点框架
二次函数 图象和性质
的符号 图象 开口方向 对称轴 顶点坐标 性质
a>0 向上 y轴 (0,0) 当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小;当x=0时,y有最小值0.
a<0 向下 y轴 (0,0) 当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大;当x=0时,y有最大值0.
例题练习
03
例题
例1.当ab>0时,y=ax 与y=ax+b的图象大致是( )
例2.二次函数y=(k+1)x2的图象如图,则k的取值范围为________.
例题
例3. 的顶点坐标是( ),对称轴是________,开口向________;
例4.下列各点:(-1,2),(-1,-2),(-2,-4),(-2,4),其中在二次函数y=-2x 的图象上的是____.
例5.抛物线y=2x ,y=-2x ,y= x 的共同性质是( )
A.开口向上 B.对称轴是y轴
C.都有最高点 D.y随x的增大而增大
例题
例6.关于函数y=3x 的性质表述正确的一项是( )
A.无论x为任何实数,y的值总为正
B.当x值增大时,y的值也增大
C.它的图象关于y轴对称
D.它的图象在第一、三象限内
例7.已知点(-1,y ),(2,y ),(-3,y )都在函数y=x 的图象上,则( )
A.y
1.在如图所示网格内建立恰当直角坐标系后,画出函数y=2x 和y=- x 的图象,并根据图象回答下列问题(设小方格的边长为1):
(1)说出这两个函数图象的开口方向,对称轴和顶点坐标;
(2)抛物线y=2x ,当x______时,抛物线上的点都在x轴
的上方,它的顶点是图象的最______点;
(3)函数y=- x ,对于一切x的值,总有函数y______0;
当x______时,y有最______值是______.
练习
2.写出图象经过点(-1,1)的一个二次函数解析式是_____________.
3.已知二次函数y=(m-2)x 的图象开口向下,则m的取值范围是_______
4.下列各点:(-1,2),(-1,-2),(-2,-4),(-2,4),其中在二次函数y=-2x 的图象上的是________________.
5.已知二次函数y=ax 的图象经过点A(-1,- ).
(1)求这个二次函数的解析式并画出其图象;
(2)请说出这个二次函数的顶点坐标、对称轴.
作业布置
04
作业布置
1.已知二次函数y=ax 的图象经过点A(-1,- ).
(1)求这个二次函数的解析式并画出其图象;
(2)请说出这个二次函数的顶点坐标、对称轴.
作业布置
2.下列四个二次函数:①y=x2,②y=-2x2,③y=x2,④y=3x2,其中抛物线开口从大到小的排列顺序是_____________
3.二次函数y=-6x2,当x1>x2>0时,y1与y2的大小关系为____________.
4.分别求出符合下列条件的抛物线y=ax 的解析式:
(1)经过点(-3,2);
(2)与y=x2开口大小相同,方向相反.
作业布置
5.已知二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A、B两点,如图所示,其中A(-1,-1),求△OAB的面积.
下节课见!
同课章节目录
