2021—2022学年人教版九年级数学上册第21章 一元二次方程 同步训练(word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学上册第21章 一元二次方程 同步训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 316.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 00:00:00 | ||
图片预览




文档简介
第21章《一元二次方程》同步训练
2021—2022学年人教版九年级数学上册
一、单选题
1.关于x的一元二次方程(a﹣5)x2﹣4x﹣1=0有实数根,则a满足( )
A.a≥1 B.a>1且a≠5 C.a≥1且a≠5 D.a≠5
2.用配方法解方程,下列配方正确的是( )
A. B. C. D.
3.已知,则代数式的值是( )
A. B. C. D.
4.如果关于x的一元二次方程ax2+x﹣1=0有实数根,则a的取值范围是( )
A.a>﹣ B.a≥﹣ C.a≥﹣且a≠0 D.a>且a≠0
5.小刚在解关于x的方程时,只抄对了,,解出其中一个根是.他核对时发现所抄的c比原方程的c值小2.则原方程的根的情况是( )
A.不存在实数根 B.有两个不相等的实数根 C.有一个根是x=-1 D.有两个相等的实数根
6.某市从2018年开始大力发展旅游产业.据统计,该市2018年旅游收入约为2亿元.预计2020年旅游收入约达到2.88亿元,设该市旅游收入的年平均增长率为x,下面所列方程正确的是( )
A.2(1+x)2=2.88 B.2x2=2.88 C.2(1+x%)2=2.88 D.2(1+x)+2(1+x)2=2.88
7.已知方程x2-x+2m=0有两个实数根,则的化简结果是( )
A.m-1 B.m+1 C.1-m D.±(m-1)
8.若|x2﹣4x+4|与互为相反数,则x+y的值为( )
A.3 B.4 C.6 D.9
9.共享单车为市民出行带来了方便,某单车公司第一个月投放1000辆单车,计划第三个月投放单车数量比第一个月多440辆.设该公司第二、三两个月投放单车数量的月平均增长率为x,则所列方程正确的为( )
A.1000(1+x)2=1000+440 B.1000(1+x)2=440
C.440(1+x)2=1000 D.1000(1+2x)=1000+440
10.目前以等为代表的战略性新兴产业蓬勃发展.某市2019年底有用户2万户,计划到2021年底全市用户数累计达到8.72万户.设全市用户数年平均增长率为,则值为( )
A. B. C. D.
11.已知一元二次方程(a+1)x2﹣ax+a2﹣a﹣2=0的一个根与方程(a+1)x2+ax﹣a2+a+2=0的一个根互为相反数,那么(a+1)x2+ax﹣a2+a+2=0的根是( )
A.0,﹣ B.0, C.﹣1,2 D.1,﹣2
12.若,是方程的两个不相等的实数根,则代数式的值是( )
A. B. C. D.
二、填空题
13.若x1,x2是一元二次方程x2+10x﹣1=0的两个根,则(x1+1)(x2+1)的值是__.
14.若关于的一元二次方程有两个不相等的实数根,则的取值范围是______.
15.某服装店经销一种品牌服装,平均每天可销售20件,每件赢利44元,经市场预测发现:在每件降价不超过10元的情况下,若每件降价1元,则每天可多销售5件,若该专卖店要使该品牌服装每天的赢利为1600元,则每件应降价_________元.
16.用换元法解方程﹣=1,设y=,那么原方程可以化为关于y的整式方程为_____.
17.如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,则AB的长度是 m(可利用的围墙长度超过6m).
三、解答题
18.按要求解方程.
(1)(直接开方法)
(2)(公式法)
(3)(因式分解)
(4)(配方法)
19.已知关于x的一元二次方程(m为常数).
(1)求证:不论m为何值,该方程总有两个不相等的实数根;
(2)若该方程一个根为3,求m的值.
20.阅读下面的材料:
我们可以用配方法求一个二次三项式的最大值或最小值,例如:求代数式的最小值.方法如下:
∵,由,得;
∴代数式的最小值是4.
(1)仿照上述方法求代数式的最小值.
(2)代数式有最大值还是最小值?请用配方法求出这个最值.
21.如图等腰直角三角形ABC中,AB=BC=8,点P从点A开始以每秒2个单位长度的速度沿AB边向点B运动,过点P作PR∥BC、PQ∥AC分别交AC、BC于R、Q.问:
(1)平行四边形PQCR面积能否为7?如果能,请求出P点运动所需要的时间;如不能,请说明理由;
(2)平行四边形PQCR面积能否为16?能为20吗?如果能,请求分别出P点运动所需要的时间;如不能,请说明理由.
22.已知:关于x的方程,
(1)求证:无论k取任何实数值,方程总有实数根;
(2)若等腰三角形ABC的一边长a=1,两个边长b,c恰好是这个方程的两个根,求△ABC的周长.
23.如图,在中,,,.
(1)点从点开始沿边向以的速度移动,点从点开始沿边向点以的速度移动.如果点,分别从,同时出发,经过几秒,的面积等于?
(2)点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动.如果点,分别从,同时出发,线段能否将分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
(3)若点沿线段方向从点出发以的速度向点移动,点沿射线方向从点出发以的速度移动,,同时出发,问几秒后,的面积为?
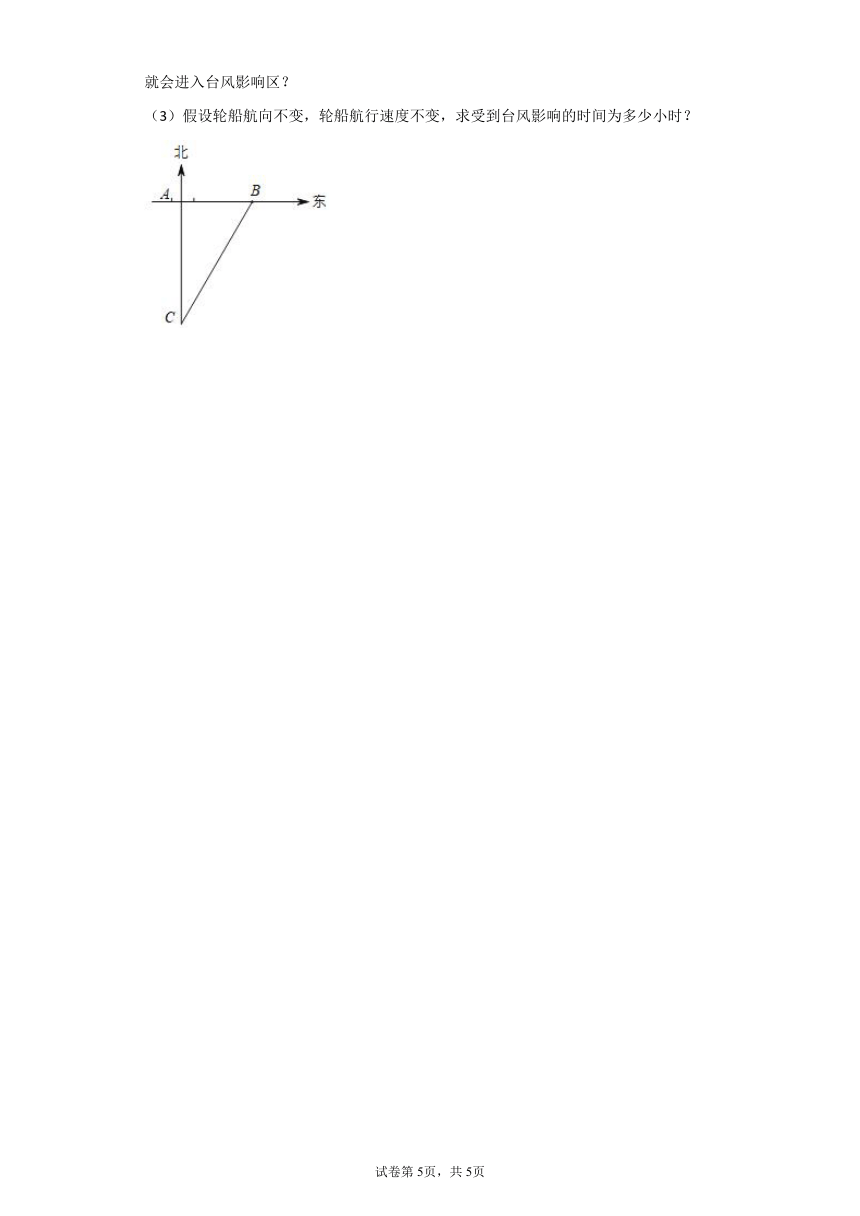
24.如图,一艘轮船以30km/h的速度沿既定航线由南向北航行,途中接到台风警报,某台风中心正以10km/h的速度由东向西移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离AB=300km.
(1)如果这艘船不改变航向,那么它会不会进入台风影响区?
(2)如果你认为这艘轮船会进入台风影响区,那么从接到警报开始,经过多长时间它就会进入台风影响区?
(3)假设轮船航向不变,轮船航行速度不变,求受到台风影响的时间为多少小时?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
2.A
3.D
4.C
5.A
6.A
7.C
8.A
9.A
10.C
11.A
12.A
13.-10
14.且
15.4
16.y2+y﹣2=0
17.1或2
18.
解:(1)
(2)
(3)
或
(4)
19.解:(1)原方程可化为.
因为a1,,,
所以.
所以不论m为何值,该方程总有两个不相等的实数根.
(2)因为一个根为3,将x3代入,得
.
解这个方程,得,.
所以m的值为3或1.
20.
解:(1)∵,由,
得 ;
∴代数式的最小值是;
(2),
∵,
∴,
∴代数式有最大值,最大值为32.
21.
解:(1)设动点P从A点出发移动x个单位时,□PQCR的面积等于7,依题意有:
×82﹣x2﹣(8﹣x)2=7,
解得:x1=1,x2=7.
故运动时间是或秒.
答:当动点P从A点出发移动或秒时,□PQCR的面积等于7.
(2)由题意得:
×82﹣x2﹣(8﹣x)2=16,
解得:x1=x2=4,
此时运动时间为:=2(秒),
×82﹣x2﹣(8﹣x)2=20,
此方程无解.
所以当动点P从A点出发移动2秒时,□PQCR的面积等于16.不存在□PQCR的面积等于20.
22.
(1)∵判别式△=[-(k+2)] -4×2k=k -4k+4=(k-2) ≥0,
∴无论k取任何实数值,方程总有实数根.
(2)当a=1为底边时,则b=c,
∴△=(k-2) =0,
解得:k=2,
∴方程为x2-4x+4=0,
解得:x1=x2=2,即b=c=2,
∵1、2、2可以构成三角形,
∴△ABC的周长为:1+2+2=5.
当a=1为一腰时,则方程有一个根为1,
∴1-(k+2)+2k=0,
解得:k=1,
∴方程为x2-3x+2=0,
解得:x1=1,x2=2,
∵1+1=2,
∴1、1、2不能构成三角形,
综上所述:△ABC的周长为5.
23.
解:(1)设经过秒,的面积等于,依题意有
,
解得,,
经检验,,均符合题意.
答:经过2秒或4秒,的面积等于.
(2)设经过秒,线段将分成面积相等的两部分,依题意有
,
化简可得.
∵.∴此方程无实数根.
∴线段不能将分成面积相等的两部分.
(3)当点在线段上,点在线段上时,
设经过秒,的面积为.
依题意有,
解得(舍去),,
∴;
当点在线段上,点在线段的延长线上时,
设经过秒,的面积为.
依题意有,,
解得.
经检验,符合题意.
综上所述,经过秒或5秒,的面积为.
24.
解:(1)如图易知AB′=300﹣10t,AC′=400﹣30t,
当B′C′=200时,将受到台风影响,
根据勾股定理可得:(300﹣10t)2+(400﹣30t)2=2002,
整理得到:t2﹣30t+210=0,
解得t=15±,
由此可知,如果这艘船不改变航向,那么它会进入台风影响区.
(2)由(1)可知经过(15﹣)h就会进入台风影响区;
(3)由(1)可知受到台风影响的时间为:15+﹣(15﹣)=2 h.
答案第1页,共2页
答案第1页,共2页
2021—2022学年人教版九年级数学上册
一、单选题
1.关于x的一元二次方程(a﹣5)x2﹣4x﹣1=0有实数根,则a满足( )
A.a≥1 B.a>1且a≠5 C.a≥1且a≠5 D.a≠5
2.用配方法解方程,下列配方正确的是( )
A. B. C. D.
3.已知,则代数式的值是( )
A. B. C. D.
4.如果关于x的一元二次方程ax2+x﹣1=0有实数根,则a的取值范围是( )
A.a>﹣ B.a≥﹣ C.a≥﹣且a≠0 D.a>且a≠0
5.小刚在解关于x的方程时,只抄对了,,解出其中一个根是.他核对时发现所抄的c比原方程的c值小2.则原方程的根的情况是( )
A.不存在实数根 B.有两个不相等的实数根 C.有一个根是x=-1 D.有两个相等的实数根
6.某市从2018年开始大力发展旅游产业.据统计,该市2018年旅游收入约为2亿元.预计2020年旅游收入约达到2.88亿元,设该市旅游收入的年平均增长率为x,下面所列方程正确的是( )
A.2(1+x)2=2.88 B.2x2=2.88 C.2(1+x%)2=2.88 D.2(1+x)+2(1+x)2=2.88
7.已知方程x2-x+2m=0有两个实数根,则的化简结果是( )
A.m-1 B.m+1 C.1-m D.±(m-1)
8.若|x2﹣4x+4|与互为相反数,则x+y的值为( )
A.3 B.4 C.6 D.9
9.共享单车为市民出行带来了方便,某单车公司第一个月投放1000辆单车,计划第三个月投放单车数量比第一个月多440辆.设该公司第二、三两个月投放单车数量的月平均增长率为x,则所列方程正确的为( )
A.1000(1+x)2=1000+440 B.1000(1+x)2=440
C.440(1+x)2=1000 D.1000(1+2x)=1000+440
10.目前以等为代表的战略性新兴产业蓬勃发展.某市2019年底有用户2万户,计划到2021年底全市用户数累计达到8.72万户.设全市用户数年平均增长率为,则值为( )
A. B. C. D.
11.已知一元二次方程(a+1)x2﹣ax+a2﹣a﹣2=0的一个根与方程(a+1)x2+ax﹣a2+a+2=0的一个根互为相反数,那么(a+1)x2+ax﹣a2+a+2=0的根是( )
A.0,﹣ B.0, C.﹣1,2 D.1,﹣2
12.若,是方程的两个不相等的实数根,则代数式的值是( )
A. B. C. D.
二、填空题
13.若x1,x2是一元二次方程x2+10x﹣1=0的两个根,则(x1+1)(x2+1)的值是__.
14.若关于的一元二次方程有两个不相等的实数根,则的取值范围是______.
15.某服装店经销一种品牌服装,平均每天可销售20件,每件赢利44元,经市场预测发现:在每件降价不超过10元的情况下,若每件降价1元,则每天可多销售5件,若该专卖店要使该品牌服装每天的赢利为1600元,则每件应降价_________元.
16.用换元法解方程﹣=1,设y=,那么原方程可以化为关于y的整式方程为_____.
17.如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,则AB的长度是 m(可利用的围墙长度超过6m).
三、解答题
18.按要求解方程.
(1)(直接开方法)
(2)(公式法)
(3)(因式分解)
(4)(配方法)
19.已知关于x的一元二次方程(m为常数).
(1)求证:不论m为何值,该方程总有两个不相等的实数根;
(2)若该方程一个根为3,求m的值.
20.阅读下面的材料:
我们可以用配方法求一个二次三项式的最大值或最小值,例如:求代数式的最小值.方法如下:
∵,由,得;
∴代数式的最小值是4.
(1)仿照上述方法求代数式的最小值.
(2)代数式有最大值还是最小值?请用配方法求出这个最值.
21.如图等腰直角三角形ABC中,AB=BC=8,点P从点A开始以每秒2个单位长度的速度沿AB边向点B运动,过点P作PR∥BC、PQ∥AC分别交AC、BC于R、Q.问:
(1)平行四边形PQCR面积能否为7?如果能,请求出P点运动所需要的时间;如不能,请说明理由;
(2)平行四边形PQCR面积能否为16?能为20吗?如果能,请求分别出P点运动所需要的时间;如不能,请说明理由.
22.已知:关于x的方程,
(1)求证:无论k取任何实数值,方程总有实数根;
(2)若等腰三角形ABC的一边长a=1,两个边长b,c恰好是这个方程的两个根,求△ABC的周长.
23.如图,在中,,,.
(1)点从点开始沿边向以的速度移动,点从点开始沿边向点以的速度移动.如果点,分别从,同时出发,经过几秒,的面积等于?
(2)点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动.如果点,分别从,同时出发,线段能否将分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
(3)若点沿线段方向从点出发以的速度向点移动,点沿射线方向从点出发以的速度移动,,同时出发,问几秒后,的面积为?
24.如图,一艘轮船以30km/h的速度沿既定航线由南向北航行,途中接到台风警报,某台风中心正以10km/h的速度由东向西移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离AB=300km.
(1)如果这艘船不改变航向,那么它会不会进入台风影响区?
(2)如果你认为这艘轮船会进入台风影响区,那么从接到警报开始,经过多长时间它就会进入台风影响区?
(3)假设轮船航向不变,轮船航行速度不变,求受到台风影响的时间为多少小时?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
2.A
3.D
4.C
5.A
6.A
7.C
8.A
9.A
10.C
11.A
12.A
13.-10
14.且
15.4
16.y2+y﹣2=0
17.1或2
18.
解:(1)
(2)
(3)
或
(4)
19.解:(1)原方程可化为.
因为a1,,,
所以.
所以不论m为何值,该方程总有两个不相等的实数根.
(2)因为一个根为3,将x3代入,得
.
解这个方程,得,.
所以m的值为3或1.
20.
解:(1)∵,由,
得 ;
∴代数式的最小值是;
(2),
∵,
∴,
∴代数式有最大值,最大值为32.
21.
解:(1)设动点P从A点出发移动x个单位时,□PQCR的面积等于7,依题意有:
×82﹣x2﹣(8﹣x)2=7,
解得:x1=1,x2=7.
故运动时间是或秒.
答:当动点P从A点出发移动或秒时,□PQCR的面积等于7.
(2)由题意得:
×82﹣x2﹣(8﹣x)2=16,
解得:x1=x2=4,
此时运动时间为:=2(秒),
×82﹣x2﹣(8﹣x)2=20,
此方程无解.
所以当动点P从A点出发移动2秒时,□PQCR的面积等于16.不存在□PQCR的面积等于20.
22.
(1)∵判别式△=[-(k+2)] -4×2k=k -4k+4=(k-2) ≥0,
∴无论k取任何实数值,方程总有实数根.
(2)当a=1为底边时,则b=c,
∴△=(k-2) =0,
解得:k=2,
∴方程为x2-4x+4=0,
解得:x1=x2=2,即b=c=2,
∵1、2、2可以构成三角形,
∴△ABC的周长为:1+2+2=5.
当a=1为一腰时,则方程有一个根为1,
∴1-(k+2)+2k=0,
解得:k=1,
∴方程为x2-3x+2=0,
解得:x1=1,x2=2,
∵1+1=2,
∴1、1、2不能构成三角形,
综上所述:△ABC的周长为5.
23.
解:(1)设经过秒,的面积等于,依题意有
,
解得,,
经检验,,均符合题意.
答:经过2秒或4秒,的面积等于.
(2)设经过秒,线段将分成面积相等的两部分,依题意有
,
化简可得.
∵.∴此方程无实数根.
∴线段不能将分成面积相等的两部分.
(3)当点在线段上,点在线段上时,
设经过秒,的面积为.
依题意有,
解得(舍去),,
∴;
当点在线段上,点在线段的延长线上时,
设经过秒,的面积为.
依题意有,,
解得.
经检验,符合题意.
综上所述,经过秒或5秒,的面积为.
24.
解:(1)如图易知AB′=300﹣10t,AC′=400﹣30t,
当B′C′=200时,将受到台风影响,
根据勾股定理可得:(300﹣10t)2+(400﹣30t)2=2002,
整理得到:t2﹣30t+210=0,
解得t=15±,
由此可知,如果这艘船不改变航向,那么它会进入台风影响区.
(2)由(1)可知经过(15﹣)h就会进入台风影响区;
(3)由(1)可知受到台风影响的时间为:15+﹣(15﹣)=2 h.
答案第1页,共2页
答案第1页,共2页
同课章节目录
