四川省双流市棠中外语学校2013届高三9月月考数学(理)试题
文档属性
| 名称 | 四川省双流市棠中外语学校2013届高三9月月考数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 473.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-21 19:50:15 | ||
图片预览




文档简介
双流市棠中外语学校2013届高三9月月考
数学(理)试题
一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.已知,为集合的非空真子集,且,不相等,若,则 ( A ).
A. B. C. D.
2.若展开式各项系数和为256,设 为虚数单位,复数的运算结果为( B )
A.4 B.-4 C.2 D.-2
3.一个几何体的三视图如图所示,则该几何体的体积为( A )
A.12 B.11 C. D.
4.如图所示的方格纸中有定点,则( C )
A. B. C. D.
5.如图,长方形的四个顶点为,曲线经过点.现将一质点随机投入长方形中,则质点落在图中阴影区域的概率是( C )
A. B. C. D.
6.已知:命题:“是的充分必要条件”;
命题:“”.则下列命题正确的是( B )
A.命题“∧”是真命题 B.命题“(┐)∧”是真命题
C.命题“∧(┐)”是真命题 D.命题“(┐)∧(┐)”是真命题
7.若数列的前n项和为,则下列命题:
(1)若数列是递增数列,则数列也是递增数列;
(2)数列是递增数列的充要条件是数列的各项均为正数;
(3)若是等差数列(公差),则的充要条件是
(4)若是等比数列,则的充要条件是
其中,正确命题的个数是( B )
A.0个 B.1个 C.2个 D.3个
8.两二面角的的两个半平面分别垂直,则这两个二面角的大小关系是( D )
A.一定相等 B.一定互补 C.一定相等或互补 D.以上都不对
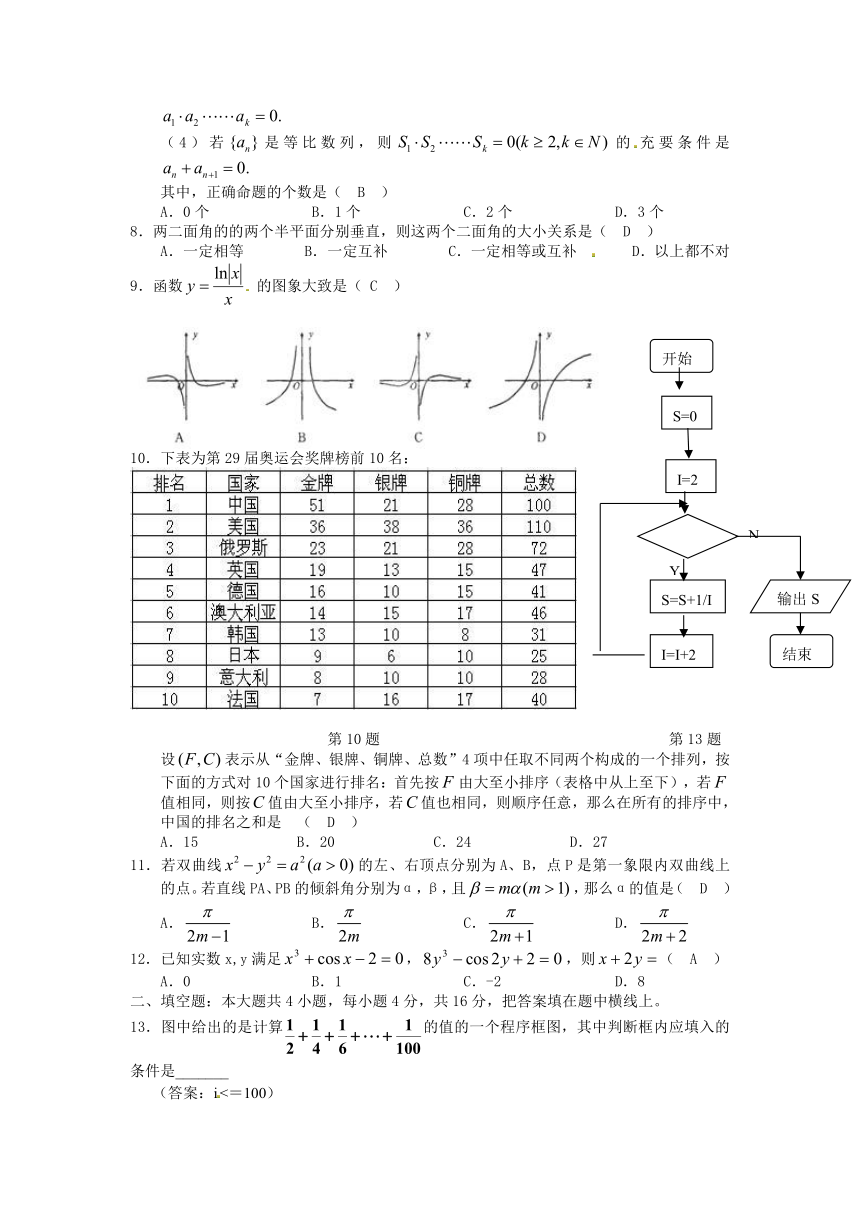
9.函数 的图象大致是( C )
10.下表为第29届奥运会奖牌榜前10名:
第10题 第13题
设表示从“金牌、银牌、铜牌、总数”4项中任取不同两个构成的一个排列,按下面的方式对10个国家进行排名:首先按由大至小排序(表格中从上至下),若值相同,则按值由大至小排序,若值也相同,则顺序任意,那么在所有的排序中,中国的排名之和是 ( D )
A.15 B.20 C.24 D.27
11.若双曲线的左、右顶点分别为A、B,点P是第一象限内双曲线上的点。若直线PA、PB的倾斜角分别为α,β,且,那么α的值是( D )
A. B. C. D.
12.已知实数x,y满足,,则( A )
A.0 B.1 C.-2 D.8
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13.图中给出的是计算的值的一个程序框图,其中判断框内应填入的条件是_______
(答案:i<=100)
14.在极坐标系中,点M到曲线ρcos=2上的点的距离的最小值为_______(答案:2)
15.已知,,,。
根据以上等式,可猜想出的一般结论是 ;
(答案: ,)
16.设的内角所对的边为;则下列命题正确的是
①若;则 ②若;则 ③若;则
④若;则 ⑤若;则
(答案:①②⑤)
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
已知函数.
(Ⅰ)求的最小正周期;
(Ⅱ)若将的图象向右平移个单位,得到函数的图象,求函数在区间上的最大值和最小值.
18.(本小题满分12分)在今年伦敦奥运会期间,来自美国和英国的共计6名志愿者被随机地平均分配到跳水、篮球、体操这三个岗位服务,且跳水岗位至少有一名美国志愿者的概率是.
(Ⅰ)求6名志愿者中来自美国、英国的各几人;
(Ⅱ)求篮球岗位恰好美国人、英国人各一人的概率。
(Ⅲ)设随机变量为在体操岗位服务的美国志愿者的个数,求的分布列及期望
解:(Ⅰ)记至少一名美国志愿者被分到跳水岗位为事件,则的对立事件为“没有美国志愿者被分到跳水岗位”,设有美国人个,,那么,解得,即来自美国的2人,来自英国的4人。 (4分)
(Ⅱ)记篮球岗位恰好美国人、英国人各有一人为事件,那么,
所以篮球岗位恰好美国人、英国人各一人的概率是. (8分)
(3)的所有可能值为0,1,2,
,,,故有分布列:
0 1 2
P
(10分)
从而(人)。 (12分)
19.(本小题满分12分)如图,是圆的直径,点在圆上,,交于点,平面,,.
(Ⅰ)证明:;
(Ⅱ)求平面与平面所成的锐二面角的余弦值.
(Ⅱ)延长交于,连,过作,连结.
由(1)知平面,平面,
.
而,平面.
平面,
,
为平面与平面所成的
二面角的平面角. ……………………8分
在中,,,
.
由,得.
.
又,
,则. ………………………………11分
是等腰直角三角形,.
平面与平面所成的锐二面角的余弦值为. ………………………12分
(法二)(Ⅰ)同法一,得. ………………………3分
如图,以为坐标原点,垂直于、、所在的直线为轴建立空间直角坐标系.
由已知条件得,
. ………4分
由,
得, . ……………6分
(Ⅱ)由(1)知.
设平面的法向量为,
由 得,
令得,, …………………………9分
由已知平面,所以取面的法向量为,
设平面与平面所成的锐二面角为,
则, …………………………11分
平面与平面所成的锐二面角的余弦值为. ……………………12分
20.(本小题满分12分)
(本小题满分12分)已知数列和满足:
, 其中为实数,为正整数.
(Ⅰ)对任意实数,证明数列不是等比数列;
(Ⅱ)对于给定的实数,试求数列的前项和;
(Ⅲ)设,是否存在实数,使得对任意正整数,都有成立 若存在,求的取值范围;若不存在,说明理由.
.解:(Ⅰ)证明:假设存在一个实数,使{}是等比数列,
则有,
即矛盾.
所以{}不是等比数列. …………………………4分
(Ⅱ)因为
又,所以
当,,此时
当时,, ,
此时,数列{}是以为首项,为公比的等比数列.
∴ …………………………8分
21.(本小题满分12分)直线与椭圆交于,两点,已知,,若且椭圆的离心率,又椭圆经过点,为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线过椭圆的焦点(为半焦距),求直线的斜率的值;
(Ⅲ)试问:的面积是否为定值?如果是,请给予证明;如果不是,请说明理由。
解析:
(Ⅰ)∵ …………………2分
∴
∴椭圆的方程为 ………………3分
(Ⅱ)依题意,设的方程为
由
显然
………………5分
由已知得:
解得 ……………………6分
22.(本小题满分14分)
已知函数.
(Ⅰ)当时,如果函数仅有一个零点,求实数的取值范围;
(Ⅱ)当时,试比较与1的大小;
(Ⅲ)求证:.
解:(Ⅰ)当时,,定义域是,
, 令,得或. …2分
当或时,,当时,,
函数在、上单调递增,在上单调递减. ……………4分
的极大值是,极小值是.
当时,; 当时,,
当仅有一个零点时,的取值范围是或.……………5分
(Ⅲ)(法一)根据(2)的结论,当时,,即.
令,则有, . ……………12分
, . ……………14分
(法二)当时,.
,,即时命题成立. ………………………………10分
设当时,命题成立,即 .
时,.
根据(Ⅱ)的结论,当时,,即.
令,则有,
则有,即时命题也成立.……………13分
因此,由数学归纳法可知不等式成立. ………………………………14分
(法三)如图,根据定积分的定义,
得.……11分
,
. ………………………………12分
,
又,,
.
. …………………………………14分
开始
S=0
I=2
S=S+1/I
I=I+2
N
输出S
结束
Y
A
B
C
E
F
M
O
H
G
A
B
C
E
F
M
O
x
y
z
A
B
C
E
F
M
O
1 2 3
4 5 6 n-1 n
…
数学(理)试题
一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.已知,为集合的非空真子集,且,不相等,若,则 ( A ).
A. B. C. D.
2.若展开式各项系数和为256,设 为虚数单位,复数的运算结果为( B )
A.4 B.-4 C.2 D.-2
3.一个几何体的三视图如图所示,则该几何体的体积为( A )
A.12 B.11 C. D.
4.如图所示的方格纸中有定点,则( C )
A. B. C. D.
5.如图,长方形的四个顶点为,曲线经过点.现将一质点随机投入长方形中,则质点落在图中阴影区域的概率是( C )
A. B. C. D.
6.已知:命题:“是的充分必要条件”;
命题:“”.则下列命题正确的是( B )
A.命题“∧”是真命题 B.命题“(┐)∧”是真命题
C.命题“∧(┐)”是真命题 D.命题“(┐)∧(┐)”是真命题
7.若数列的前n项和为,则下列命题:
(1)若数列是递增数列,则数列也是递增数列;
(2)数列是递增数列的充要条件是数列的各项均为正数;
(3)若是等差数列(公差),则的充要条件是
(4)若是等比数列,则的充要条件是
其中,正确命题的个数是( B )
A.0个 B.1个 C.2个 D.3个
8.两二面角的的两个半平面分别垂直,则这两个二面角的大小关系是( D )
A.一定相等 B.一定互补 C.一定相等或互补 D.以上都不对
9.函数 的图象大致是( C )
10.下表为第29届奥运会奖牌榜前10名:
第10题 第13题
设表示从“金牌、银牌、铜牌、总数”4项中任取不同两个构成的一个排列,按下面的方式对10个国家进行排名:首先按由大至小排序(表格中从上至下),若值相同,则按值由大至小排序,若值也相同,则顺序任意,那么在所有的排序中,中国的排名之和是 ( D )
A.15 B.20 C.24 D.27
11.若双曲线的左、右顶点分别为A、B,点P是第一象限内双曲线上的点。若直线PA、PB的倾斜角分别为α,β,且,那么α的值是( D )
A. B. C. D.
12.已知实数x,y满足,,则( A )
A.0 B.1 C.-2 D.8
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13.图中给出的是计算的值的一个程序框图,其中判断框内应填入的条件是_______
(答案:i<=100)
14.在极坐标系中,点M到曲线ρcos=2上的点的距离的最小值为_______(答案:2)
15.已知,,,。
根据以上等式,可猜想出的一般结论是 ;
(答案: ,)
16.设的内角所对的边为;则下列命题正确的是
①若;则 ②若;则 ③若;则
④若;则 ⑤若;则
(答案:①②⑤)
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
已知函数.
(Ⅰ)求的最小正周期;
(Ⅱ)若将的图象向右平移个单位,得到函数的图象,求函数在区间上的最大值和最小值.
18.(本小题满分12分)在今年伦敦奥运会期间,来自美国和英国的共计6名志愿者被随机地平均分配到跳水、篮球、体操这三个岗位服务,且跳水岗位至少有一名美国志愿者的概率是.
(Ⅰ)求6名志愿者中来自美国、英国的各几人;
(Ⅱ)求篮球岗位恰好美国人、英国人各一人的概率。
(Ⅲ)设随机变量为在体操岗位服务的美国志愿者的个数,求的分布列及期望
解:(Ⅰ)记至少一名美国志愿者被分到跳水岗位为事件,则的对立事件为“没有美国志愿者被分到跳水岗位”,设有美国人个,,那么,解得,即来自美国的2人,来自英国的4人。 (4分)
(Ⅱ)记篮球岗位恰好美国人、英国人各有一人为事件,那么,
所以篮球岗位恰好美国人、英国人各一人的概率是. (8分)
(3)的所有可能值为0,1,2,
,,,故有分布列:
0 1 2
P
(10分)
从而(人)。 (12分)
19.(本小题满分12分)如图,是圆的直径,点在圆上,,交于点,平面,,.
(Ⅰ)证明:;
(Ⅱ)求平面与平面所成的锐二面角的余弦值.
(Ⅱ)延长交于,连,过作,连结.
由(1)知平面,平面,
.
而,平面.
平面,
,
为平面与平面所成的
二面角的平面角. ……………………8分
在中,,,
.
由,得.
.
又,
,则. ………………………………11分
是等腰直角三角形,.
平面与平面所成的锐二面角的余弦值为. ………………………12分
(法二)(Ⅰ)同法一,得. ………………………3分
如图,以为坐标原点,垂直于、、所在的直线为轴建立空间直角坐标系.
由已知条件得,
. ………4分
由,
得, . ……………6分
(Ⅱ)由(1)知.
设平面的法向量为,
由 得,
令得,, …………………………9分
由已知平面,所以取面的法向量为,
设平面与平面所成的锐二面角为,
则, …………………………11分
平面与平面所成的锐二面角的余弦值为. ……………………12分
20.(本小题满分12分)
(本小题满分12分)已知数列和满足:
, 其中为实数,为正整数.
(Ⅰ)对任意实数,证明数列不是等比数列;
(Ⅱ)对于给定的实数,试求数列的前项和;
(Ⅲ)设,是否存在实数,使得对任意正整数,都有成立 若存在,求的取值范围;若不存在,说明理由.
.解:(Ⅰ)证明:假设存在一个实数,使{}是等比数列,
则有,
即矛盾.
所以{}不是等比数列. …………………………4分
(Ⅱ)因为
又,所以
当,,此时
当时,, ,
此时,数列{}是以为首项,为公比的等比数列.
∴ …………………………8分
21.(本小题满分12分)直线与椭圆交于,两点,已知,,若且椭圆的离心率,又椭圆经过点,为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线过椭圆的焦点(为半焦距),求直线的斜率的值;
(Ⅲ)试问:的面积是否为定值?如果是,请给予证明;如果不是,请说明理由。
解析:
(Ⅰ)∵ …………………2分
∴
∴椭圆的方程为 ………………3分
(Ⅱ)依题意,设的方程为
由
显然
………………5分
由已知得:
解得 ……………………6分
22.(本小题满分14分)
已知函数.
(Ⅰ)当时,如果函数仅有一个零点,求实数的取值范围;
(Ⅱ)当时,试比较与1的大小;
(Ⅲ)求证:.
解:(Ⅰ)当时,,定义域是,
, 令,得或. …2分
当或时,,当时,,
函数在、上单调递增,在上单调递减. ……………4分
的极大值是,极小值是.
当时,; 当时,,
当仅有一个零点时,的取值范围是或.……………5分
(Ⅲ)(法一)根据(2)的结论,当时,,即.
令,则有, . ……………12分
, . ……………14分
(法二)当时,.
,,即时命题成立. ………………………………10分
设当时,命题成立,即 .
时,.
根据(Ⅱ)的结论,当时,,即.
令,则有,
则有,即时命题也成立.……………13分
因此,由数学归纳法可知不等式成立. ………………………………14分
(法三)如图,根据定积分的定义,
得.……11分
,
. ………………………………12分
,
又,,
.
. …………………………………14分
开始
S=0
I=2
S=S+1/I
I=I+2
N
输出S
结束
Y
A
B
C
E
F
M
O
H
G
A
B
C
E
F
M
O
x
y
z
A
B
C
E
F
M
O
1 2 3
4 5 6 n-1 n
…
同课章节目录
