人教版九年级上册数学第二十二章 二次函数22.3实际问题与二次函数应用题压轴专题训练 (word版含答案)
文档属性
| 名称 | 人教版九年级上册数学第二十二章 二次函数22.3实际问题与二次函数应用题压轴专题训练 (word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 129.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 10:14:48 | ||
图片预览




文档简介
人教版九年级上册数学22.3实际问题与二次函数 应用题专题训练
某公司经销一种绿茶,每千克成本为 元.市场调查发现,在一段时间内,销售量 (千克)随销售单价 (元/千克)的变化而变化,具体关系式为:.设这种绿茶在这段时间内的销售利润为 (元),解答下列问题:
(1) 求 与 的关系式;
(2) 当 取何值时, 的值最大?
(3) 如果物价部门规定这种绿茶的销售单价不得高于 元/千克,公司想要在这段时间内获得 元的销售利润,销售单价应定为多少元?
如图,在足够大的空地上有一段长为 米的旧墙 ,某人利用旧墙和木栏围成一个矩形菜园 ,其中 ,已知矩形菜园的一边靠墙,另三边一共用了 米木栏.
(1) 若 ,所围成的矩形菜园的面积为 平方米,求所利用旧墙 的长;
(2) 求矩形菜园 面积的最大值.
某商场购进一种每件价格为 元的新商品,在商场试销发现:销售单价 (元/件)与每天销售量 (件)之间满足如图所示的关系:
(1) 求出 与 之间的函数关系式;
(2) 如果商店销售这种商品,每天要获得 元利润,那么每件商品的销售价应定为多少元?
(3) 写出每天的利润 与销售单价 之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
某商店经销一种双肩包,已知这种双肩包的成本价为每个 元,市场调查发现,这种双肩包每天的销售量 (单位:个)与销售单价 (单位:元)有如下关系:.
设这种双肩包每天的销售利润为 元.
(1) 求 与 之间的函数表达式;
(2) 这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3) 如果物价部门规定这种双肩包的销售单价不高于 元,该商店销售这种双肩包每天要获得 元的销售利润,销售单价应定为多少元?
某商店经销一种双肩包,已知这种双肩包的成本价为每个 元.市场调查发现,这种双肩包每天的销售量 (单位:个)与销售单价 (单位:元)有如下关系:().
设这种双肩包每天的销售利润为 元.
(1) 求 与 之间的函数表达式;
(2) 这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3) 如果物价部门规定这种双肩包的销售单价不高于 元,该商店销售这种双肩包每天要获得 元的销售利润,销售单价应定为多少元?
某商场试销售一种成本为每件 元的服装,规定试销售期间单价不低于成本单价,且获利不得高于 ,经试销发现,销售量 (件)与销售单价 (元)符合一次函数 的关系,且当 时,; 时,.
(1) 求一次函数关系式并写出 的取值范围;
(2) 若该商场获得利润为 ,试写出 与销售单价 之间的函数关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
某商店经营一种小商品,进价为 元,据市场调查,销售单价是 元时平均每天销售量是 件,而销售价每降低一元,平均每天就可以多售出 件.
(1) 假定每件商品降低 元,商店每天销售这种小商品的利润 元,请写出 与 之间的函数关系.(注:销售利润 销售收入 购进成本)
(2) 当每件小商品降低多少元时,该商店每天能获利 元?
(3) 每件小商品销售价为多少时,商店每天销售这种小商品的利润最大?最大利润是多少?
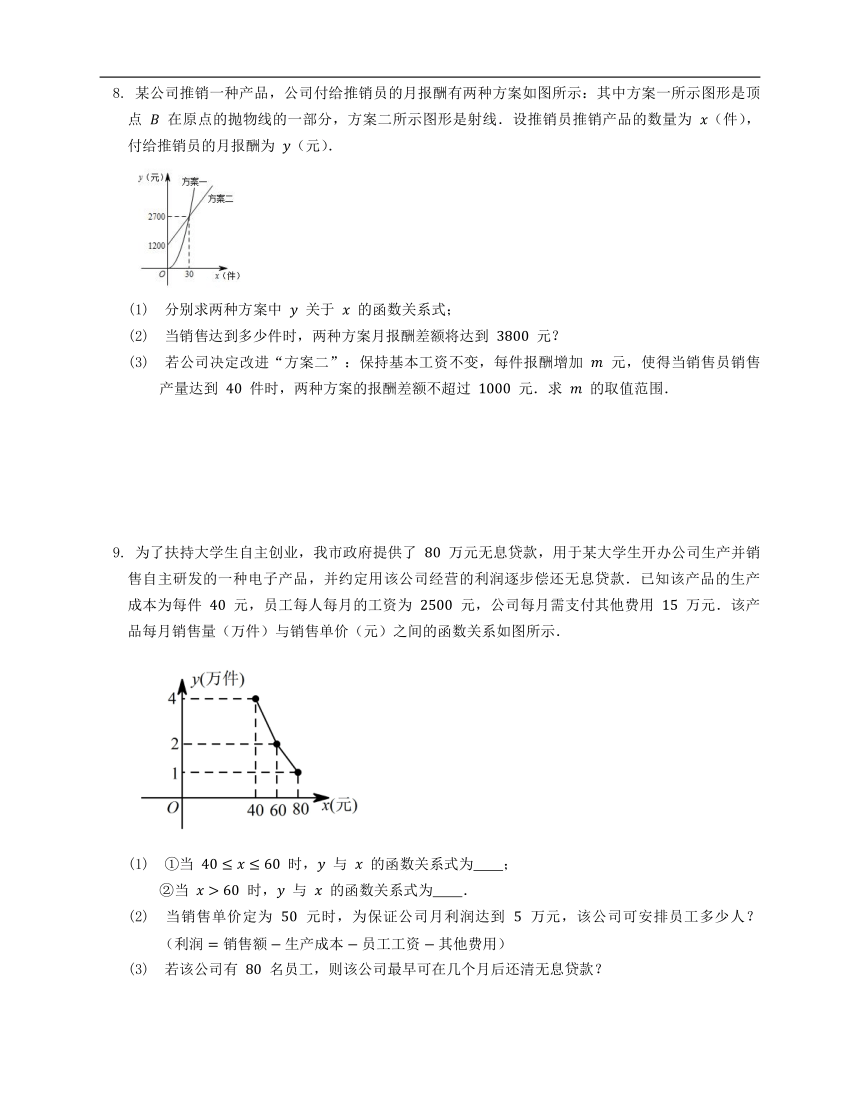
某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点 在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为 (件),付给推销员的月报酬为 (元).
(1) 分别求两种方案中 关于 的函数关系式;
(2) 当销售达到多少件时,两种方案月报酬差额将达到 元?
(3) 若公司决定改进“方案二”:保持基本工资不变,每件报酬增加 元,使得当销售员销售产量达到 件时,两种方案的报酬差额不超过 元.求 的取值范围.
为了扶持大学生自主创业,我市政府提供了 万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件 元,员工每人每月的工资为 元,公司每月需支付其他费用 万元.该产品每月销售量(万件)与销售单价(元)之间的函数关系如图所示.
(1) ①当 时, 与 的函数关系式为 ;
②当 时, 与 的函数关系式为 .
(2) 当销售单价定为 元时,为保证公司月利润达到 万元,该公司可安排员工多少人?()
(3) 若该公司有 名员工,则该公司最早可在几个月后还清无息贷款?
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润 (万元)与时间 (月)之间的关系(即前 个月的利润总和 与 之间的关系).根据图象提供的信息,解答下列问题:
(1) 求累积利润 (万元)与时间 (月)之间的函数关系式.
(2) 求截止到几月末公司累积利润可达 万元.
(3) 求第 个月公司所获利润是多少万元?
如图是某隧道截面示意图,它是由抛物线和长方形构成,已知 米, 米,抛物线顶点 到地面 的垂直距离为 米,以 所在直线为 轴,以 所在直线为 轴建立直角坐标系.
(1) 求抛物线的解析式;
(2) 由于隧道较长,需要在抛物线型拱壁上需要安装两排灯,使它们到地面的高度相同,如果灯离地面的高度不超过 米,那么两排灯的水平距离最小是多少米?
(3) 一辆特殊货运汽车载着一个长方体集装箱,集装箱宽为 ,最高处与地面距离为 ,隧道内设双向行车道,双向行车道间隔距离为 ,交通部门规定,车载货物顶部距离隧道壁的竖直距离不少于 ,才能安全通行,问这辆特殊货车能否安全通过隧道?
青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间比淡季上涨 ,下表是去年该酒店豪华间某两天的相关记录:
(1) 该酒店豪华间有多少间?旺季每间价格为多少元?
(2) 今年旺季来临,豪华间的间数不变.经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加 元,每天未入住房间数增加 间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
某商店经销一种健身球,已知这种健身球的成本价为每个 元,市场调查发现,该种健身球每天的销售量 (个)与销售单价 (元)有如下关系: , 设这种健身球每天的销售利润为 元.
(1) 求 与 之间的函数关系式;
(2) 该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3) 如果物价部门规定这种健身球的销售单价不高于 元,该商店销售这种健身球每天要获得 元的销售利润,销售单价应定为多少元?
某商店销售面向中考生的计数跳绳,每根成本为 元,销售的前 天内的日销售量 (根)与时间 (天)的关系如表.前 天每天的价格 (元/件)与时间 (天)的函数关系式为:( 且 为整数).
(1) 认真分析表中的数据,用所学过的知识确定 (件)与 (天)之间是满足一次函数的关系还是二次函数的关系?并利用这些数据求 (件)与 (天)之间得函数关系式;
(2) 请计算 天中哪一天的日销售利润最大,最大日销售利润是多少?
某网店准备销售某种品牌的笔筒,成本为 元/件,试营销阶段发现:当销售单价是 元时,每天的销售量为 件,销售单价每上涨 元,每天的销售量就减少 件.
(1) 写出销售量 (件)与销售单价 (元)之间的函数关系式;
(2) 该笔筒销售单价定为多少元时,每天获取的利润最大,最大利润是多少?
(3) 该网店店主热心公益事业,决定从该笔筒每天的销售利润中拿出 元捐给希望工程,为了保证捐款后销售该笔筒每天剩余利润不低于 元,试确定该笔筒销售单价的范围.
某商场要经营一种新上市的文具,进价为 .试营销阶段发现:当销售单价是 元时,每天的销售量为 件;销售单价每上涨 元,每天的销售量就减少 件.
(1) 写出商场销售这种文具,每天所得的销售利润 (元)与销售单价 (元)之间的函数表达式.
(2) 求销售单价为多少元时,该文具每天的销售利润最大.
(3) 商场的营销部结合上述情况,提出了 两种营销方案:
方案 :该文具的销售单价高于进价且不超过 元;
方案 :每天销售量不少于 件,且每件文具的利润至少为 元.
请比较哪种方案的最大利润更高,并说明理由.
某商品交易会上,一商人将每件进价为 元的纪念品,按每件 元出售,每天可售出 件.他想采用提高售价的办法来增加利润,经试验,发现这种纪念品每件提价 元,每天的销售量会减少 件.
(1) 当售价定为多少元时,每天的利润为 元?
(2) 写出每天所得的利润 (元)与售价 (元 件)之间的函数关系式,每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?()
小明大学毕业回家乡创业,第一期培植盆景与花卉各 盆.售后统计,盆景的平均每盆利润是 元,花卉的平均每盆利润是 元.调研发现:①盆景每增加 盆,盆景的平均每盆利润减少 元;每减少 盆,盆景的平均每盆利润增加 元;②花卉的平均每盆利润始终不变.小明计划第二期培植盆景与花卉共 盆,设培植的盆景比第一期增加 盆,第二期盆景与花卉售完后的利润分别为 ,(单位:元).
(1) 用含 的代数式分别表示 ,.
(2) 当 取何值时,第二期培植的盆景与花卉售完后获得的总利润 最大,最大总利润是多少?
一名大学生利用“互联网 ”自主创业,销售一种产品,这种产品的成本价为 元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于 元/件,市场调查发现,该产品每天的销售量 (件)与 (元/件)之间的函数关系如图所示.
(1) 求 与 之间的函数关系式,并写出自变量 的取值范围;
(2) 求每天的销售利润 (元)与销售单价 (元/件)之间的函数关系式,并求出每天销售价为多少元时,每天的销售利润最大?最大利润是多少?
某商场将进价为 元的冰箱以 元售出,平均每天能售出 台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低 元,平均每天就能多售出 台.
(1) 假设每台冰箱降价 元,商场每天销售这种冰箱的利润是 元,请写出 与 之间的函数表达式.(不要求写自变量的取值范围)
(2) 商场要想在这种冰箱销售中每天盈利 元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3) 每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
答案
一、解答题(共20题)
1. 【答案】
(1)
与 的关系式为 .
(2)
当 时, 的值最大.
(3) 当 时,可得方程 .
解这个方程,得 ,.
根据题意, 不合题意应舍去.
当销售单价为 元时,可获得销售利润 元.
2. 【答案】
(1) 设 ,则 ,
根据题意得解得当 时,,不合题意舍去;
当 时,,
答: 的长为 .
(2) 设 ,
,
当 时,则 时, 的最大值为 ;
当 时,则当 时, 随 的增大而增大,当 时, 的最大值为 ,
综上所述,当 时, 的最大值为 ;当 时, 的最大值为 .
3. 【答案】
(1) 设 与 之间的函数关系式为 ,
由所给函数图象可知:
解得:
故 与 的函数关系式为 .
(2) 根据题意,得:整理,得:解得:或答:每件商品的销售价应定为 元或 元.
(3) ,
,
当 时,,
售价定为 元/件时,每天最大利润 元.
4. 【答案】
(1)
与 之间的函数表达式为 .
(2) 根据题意得,.
,当 时, 有最大值,最大值是 .
即这种双肩包销售单价定为 元时,每天的销售利润最大,最大利润是 元.
(3) 当 时,,解得 ,.
,
不符合题意,舍去.
故该商店销售这种双肩包每天要获得 元的销售利润,销售单价应定为 元.
5. 【答案】
(1)
与 之间的函数表达式为 .
(2) 根据题意得, 当 时, 有最大值,最大值是 .
即这种双肩包销售单价定为 元时,每天的销售利润最大,最大利润是 元.
(3) 当 时,解得,
不符合题意,舍去,
故该商品销售这种双肩包每天要获得 元的销售利润,销售单价应定为 元.
6. 【答案】
(1) .
(2) .
当售价定为 元时,获得最大利润 元.
7. 【答案】
(1) .
(2) 根据题意得 ,
整理得 ,解得 ,.
答:当每件小商品降低 元或 元时,该商店每天能获利 元.
(3) ,
,
当 时, 有最大值,最大值为 .
答:每件小商品销售价为 元时,商店每天销售这种小商品的利润最大,最大利润是 元.
8. 【答案】
(1) 设 ,把 代入得,,解得 .
.
设 ,把 代入得,,解得 .
.
(2) 由题意得,.
解得 ,(舍去).
答:当销售达到 件时,按现行方案月报酬差额达到 元.
(3) 当销售员销售产量达到 件时,
方案一的月报酬为 .
方案二的月报酬为 .
由题意得
解得 .
9. 【答案】
(1) ① ;②
(2) 设安排 名员工,当单价定为 元时,销售量为 万件,所以
(3) 当 时,利润
所以 时,(万元);
当 时,利润
所以 时,(万元).
所以要尽早还清贷款,只有当单价 元时,获得最大月利润 万元,
设该公司 个月后还清贷款,则 .
所以 ,即 为所求.
10. 【答案】
(1) 由图象可知: 与 函数图象的顶点坐标为 ,过点 ,
设: 与 间的函数关系为 .
将点 代入,得:,
与 之间的函数关系式为:.
(2) 令 ,
得:,
解得 ,(舍去).
截止到 月末公司累积利润可达 万元.
(3) 令 ,,
令 ,.
第 个月所获利润为 万元.
11. 【答案】
(1) 根据题意,顶点 的坐标为 ,点 的坐标为 ,
设抛物线的解析式为 ,
把点 代入得:,
解得:,
即所求抛物线的解析式为:.
(2) 由图象可知,高度越高,两排等间的距离越近,
把 代入 得:,
解得:,,
所求最小距离为:,
答:两排灯的水平距离最小是 米.
(3) 根据题意,当 时,
,
能安全通过隧道,
答:这辆特殊货车能安全通过隧道.
12. 【答案】
(1) 设有 间豪华间,由题可得解得经检验 是原方程的根,且符合题意.
则:(元/间).
答:该酒店豪华间有 间,旺季每间价格为 元.
(2) 设上涨 元,日总收入为 ,则 ,
因为 ,
所以抛物线开口向下,
所以当 时,(元).
答:该酒店豪华间价格上涨 元时,豪华间日总收入最高,为 元.
13. 【答案】
(1) 根据题意可得:
与 之间的函数关系为 .
(2) 根据题意可得:
,
当 时, 有最大值, 最大值为 .
答:销售单价定为 元时,每天销售利润最大,最大销售利润 元.
(3) 当 时,可得方程解得 ,
不符合题意,应舍去.
答:该商店销售这种健身球每天想要获得 元的销售利润,销售单价定为 元.
14. 【答案】
(1) 由表格中数据可知,当时间 每增加 天,日销售量相应减少 件,
与 满足一次函数关系.
设 ,将 , 代入,
得: 解得:
与 的函数关系为 .
(2) 设日销售利润为 ,
则 ,
当 时, 有最大值,最大值为 元.
答:第 天时,销售利润最大,最大利润为 元.
15. 【答案】
(1) .
(2) 设每天的利润为 ,
,
,
当时 , 的最大值为 ,
答:该笔筒销售单价定为 元时,每月获取的利润最大,最大利润是 元;
(3) 捐款后销售利润为 ,
则 ,
当 时,,解得 ,,
该笔筒销售单价的范围为 .
16. 【答案】
(1) ,
与 之间的函数表达式是 .
(2)
,
有最大值,当 时,.
当销售单价为 元时,该文具每天的销售利润最大.
(3) 方案 :由题意可知 .
,对称轴是 ,
抛物线开口向下,在对称轴左侧 随 的增大而增大,
当 时, 取最大值.
(元).
方案 :由题意得 ,
,
解得 .
在对称轴右侧 随 的增大而减小,
当 时, 取最大值.
(元),
,
方案 的最大利润更高.
17. 【答案】
(1) 设售价定为 元时,每天的利润为 元,根据题意得:解得:答:售价定为 元或 元时,每天的利润为 元.
(2) 根据题意得:,
即 ,,
故当 时, 元,
答:售价为 元时,利润最大,最大利润是 元.
18. 【答案】
(1) 设培植的盆景比第一期增加 盆,
则第二期盆景有 盆,花卉有 盆.
根据题意,得:
.
.
(2) 根据题意,得:
对称轴 ,
,且 为整数.
当 时, 取得最大值,最大值为 .
答:当 时,第二期培植的盆景与花卉售完后获得的总利润 最大,最大总利润是 元.
19. 【答案】
(1) 设 与 的函数解析式为 ,
由题意得: 解得:
与 的函数解析式为 .
(2) .
,
当 时, 随 的增大而增大.
当 时, 最大,最大利润为 元.
当销售价为 元时,每天的销售利润最大,最大利润为 元.
20. 【答案】
(1) 根据题意,得 ,
即 .
(2) 由题意,得 .
整理,得 .
解这个方程,得 ,.
要使百姓得到实惠,取 .
每台冰箱应降价 元.
(3) 对于 ,
当 时,
.
每台冰箱的售价降价 元时,商场的利润最大,最大利润是 元.
某公司经销一种绿茶,每千克成本为 元.市场调查发现,在一段时间内,销售量 (千克)随销售单价 (元/千克)的变化而变化,具体关系式为:.设这种绿茶在这段时间内的销售利润为 (元),解答下列问题:
(1) 求 与 的关系式;
(2) 当 取何值时, 的值最大?
(3) 如果物价部门规定这种绿茶的销售单价不得高于 元/千克,公司想要在这段时间内获得 元的销售利润,销售单价应定为多少元?
如图,在足够大的空地上有一段长为 米的旧墙 ,某人利用旧墙和木栏围成一个矩形菜园 ,其中 ,已知矩形菜园的一边靠墙,另三边一共用了 米木栏.
(1) 若 ,所围成的矩形菜园的面积为 平方米,求所利用旧墙 的长;
(2) 求矩形菜园 面积的最大值.
某商场购进一种每件价格为 元的新商品,在商场试销发现:销售单价 (元/件)与每天销售量 (件)之间满足如图所示的关系:
(1) 求出 与 之间的函数关系式;
(2) 如果商店销售这种商品,每天要获得 元利润,那么每件商品的销售价应定为多少元?
(3) 写出每天的利润 与销售单价 之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
某商店经销一种双肩包,已知这种双肩包的成本价为每个 元,市场调查发现,这种双肩包每天的销售量 (单位:个)与销售单价 (单位:元)有如下关系:.
设这种双肩包每天的销售利润为 元.
(1) 求 与 之间的函数表达式;
(2) 这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3) 如果物价部门规定这种双肩包的销售单价不高于 元,该商店销售这种双肩包每天要获得 元的销售利润,销售单价应定为多少元?
某商店经销一种双肩包,已知这种双肩包的成本价为每个 元.市场调查发现,这种双肩包每天的销售量 (单位:个)与销售单价 (单位:元)有如下关系:().
设这种双肩包每天的销售利润为 元.
(1) 求 与 之间的函数表达式;
(2) 这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3) 如果物价部门规定这种双肩包的销售单价不高于 元,该商店销售这种双肩包每天要获得 元的销售利润,销售单价应定为多少元?
某商场试销售一种成本为每件 元的服装,规定试销售期间单价不低于成本单价,且获利不得高于 ,经试销发现,销售量 (件)与销售单价 (元)符合一次函数 的关系,且当 时,; 时,.
(1) 求一次函数关系式并写出 的取值范围;
(2) 若该商场获得利润为 ,试写出 与销售单价 之间的函数关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
某商店经营一种小商品,进价为 元,据市场调查,销售单价是 元时平均每天销售量是 件,而销售价每降低一元,平均每天就可以多售出 件.
(1) 假定每件商品降低 元,商店每天销售这种小商品的利润 元,请写出 与 之间的函数关系.(注:销售利润 销售收入 购进成本)
(2) 当每件小商品降低多少元时,该商店每天能获利 元?
(3) 每件小商品销售价为多少时,商店每天销售这种小商品的利润最大?最大利润是多少?
某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点 在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为 (件),付给推销员的月报酬为 (元).
(1) 分别求两种方案中 关于 的函数关系式;
(2) 当销售达到多少件时,两种方案月报酬差额将达到 元?
(3) 若公司决定改进“方案二”:保持基本工资不变,每件报酬增加 元,使得当销售员销售产量达到 件时,两种方案的报酬差额不超过 元.求 的取值范围.
为了扶持大学生自主创业,我市政府提供了 万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件 元,员工每人每月的工资为 元,公司每月需支付其他费用 万元.该产品每月销售量(万件)与销售单价(元)之间的函数关系如图所示.
(1) ①当 时, 与 的函数关系式为 ;
②当 时, 与 的函数关系式为 .
(2) 当销售单价定为 元时,为保证公司月利润达到 万元,该公司可安排员工多少人?()
(3) 若该公司有 名员工,则该公司最早可在几个月后还清无息贷款?
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润 (万元)与时间 (月)之间的关系(即前 个月的利润总和 与 之间的关系).根据图象提供的信息,解答下列问题:
(1) 求累积利润 (万元)与时间 (月)之间的函数关系式.
(2) 求截止到几月末公司累积利润可达 万元.
(3) 求第 个月公司所获利润是多少万元?
如图是某隧道截面示意图,它是由抛物线和长方形构成,已知 米, 米,抛物线顶点 到地面 的垂直距离为 米,以 所在直线为 轴,以 所在直线为 轴建立直角坐标系.
(1) 求抛物线的解析式;
(2) 由于隧道较长,需要在抛物线型拱壁上需要安装两排灯,使它们到地面的高度相同,如果灯离地面的高度不超过 米,那么两排灯的水平距离最小是多少米?
(3) 一辆特殊货运汽车载着一个长方体集装箱,集装箱宽为 ,最高处与地面距离为 ,隧道内设双向行车道,双向行车道间隔距离为 ,交通部门规定,车载货物顶部距离隧道壁的竖直距离不少于 ,才能安全通行,问这辆特殊货车能否安全通过隧道?
青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间比淡季上涨 ,下表是去年该酒店豪华间某两天的相关记录:
(1) 该酒店豪华间有多少间?旺季每间价格为多少元?
(2) 今年旺季来临,豪华间的间数不变.经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加 元,每天未入住房间数增加 间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
某商店经销一种健身球,已知这种健身球的成本价为每个 元,市场调查发现,该种健身球每天的销售量 (个)与销售单价 (元)有如下关系: , 设这种健身球每天的销售利润为 元.
(1) 求 与 之间的函数关系式;
(2) 该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3) 如果物价部门规定这种健身球的销售单价不高于 元,该商店销售这种健身球每天要获得 元的销售利润,销售单价应定为多少元?
某商店销售面向中考生的计数跳绳,每根成本为 元,销售的前 天内的日销售量 (根)与时间 (天)的关系如表.前 天每天的价格 (元/件)与时间 (天)的函数关系式为:( 且 为整数).
(1) 认真分析表中的数据,用所学过的知识确定 (件)与 (天)之间是满足一次函数的关系还是二次函数的关系?并利用这些数据求 (件)与 (天)之间得函数关系式;
(2) 请计算 天中哪一天的日销售利润最大,最大日销售利润是多少?
某网店准备销售某种品牌的笔筒,成本为 元/件,试营销阶段发现:当销售单价是 元时,每天的销售量为 件,销售单价每上涨 元,每天的销售量就减少 件.
(1) 写出销售量 (件)与销售单价 (元)之间的函数关系式;
(2) 该笔筒销售单价定为多少元时,每天获取的利润最大,最大利润是多少?
(3) 该网店店主热心公益事业,决定从该笔筒每天的销售利润中拿出 元捐给希望工程,为了保证捐款后销售该笔筒每天剩余利润不低于 元,试确定该笔筒销售单价的范围.
某商场要经营一种新上市的文具,进价为 .试营销阶段发现:当销售单价是 元时,每天的销售量为 件;销售单价每上涨 元,每天的销售量就减少 件.
(1) 写出商场销售这种文具,每天所得的销售利润 (元)与销售单价 (元)之间的函数表达式.
(2) 求销售单价为多少元时,该文具每天的销售利润最大.
(3) 商场的营销部结合上述情况,提出了 两种营销方案:
方案 :该文具的销售单价高于进价且不超过 元;
方案 :每天销售量不少于 件,且每件文具的利润至少为 元.
请比较哪种方案的最大利润更高,并说明理由.
某商品交易会上,一商人将每件进价为 元的纪念品,按每件 元出售,每天可售出 件.他想采用提高售价的办法来增加利润,经试验,发现这种纪念品每件提价 元,每天的销售量会减少 件.
(1) 当售价定为多少元时,每天的利润为 元?
(2) 写出每天所得的利润 (元)与售价 (元 件)之间的函数关系式,每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?()
小明大学毕业回家乡创业,第一期培植盆景与花卉各 盆.售后统计,盆景的平均每盆利润是 元,花卉的平均每盆利润是 元.调研发现:①盆景每增加 盆,盆景的平均每盆利润减少 元;每减少 盆,盆景的平均每盆利润增加 元;②花卉的平均每盆利润始终不变.小明计划第二期培植盆景与花卉共 盆,设培植的盆景比第一期增加 盆,第二期盆景与花卉售完后的利润分别为 ,(单位:元).
(1) 用含 的代数式分别表示 ,.
(2) 当 取何值时,第二期培植的盆景与花卉售完后获得的总利润 最大,最大总利润是多少?
一名大学生利用“互联网 ”自主创业,销售一种产品,这种产品的成本价为 元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于 元/件,市场调查发现,该产品每天的销售量 (件)与 (元/件)之间的函数关系如图所示.
(1) 求 与 之间的函数关系式,并写出自变量 的取值范围;
(2) 求每天的销售利润 (元)与销售单价 (元/件)之间的函数关系式,并求出每天销售价为多少元时,每天的销售利润最大?最大利润是多少?
某商场将进价为 元的冰箱以 元售出,平均每天能售出 台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低 元,平均每天就能多售出 台.
(1) 假设每台冰箱降价 元,商场每天销售这种冰箱的利润是 元,请写出 与 之间的函数表达式.(不要求写自变量的取值范围)
(2) 商场要想在这种冰箱销售中每天盈利 元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3) 每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
答案
一、解答题(共20题)
1. 【答案】
(1)
与 的关系式为 .
(2)
当 时, 的值最大.
(3) 当 时,可得方程 .
解这个方程,得 ,.
根据题意, 不合题意应舍去.
当销售单价为 元时,可获得销售利润 元.
2. 【答案】
(1) 设 ,则 ,
根据题意得解得当 时,,不合题意舍去;
当 时,,
答: 的长为 .
(2) 设 ,
,
当 时,则 时, 的最大值为 ;
当 时,则当 时, 随 的增大而增大,当 时, 的最大值为 ,
综上所述,当 时, 的最大值为 ;当 时, 的最大值为 .
3. 【答案】
(1) 设 与 之间的函数关系式为 ,
由所给函数图象可知:
解得:
故 与 的函数关系式为 .
(2) 根据题意,得:整理,得:解得:或答:每件商品的销售价应定为 元或 元.
(3) ,
,
当 时,,
售价定为 元/件时,每天最大利润 元.
4. 【答案】
(1)
与 之间的函数表达式为 .
(2) 根据题意得,.
,当 时, 有最大值,最大值是 .
即这种双肩包销售单价定为 元时,每天的销售利润最大,最大利润是 元.
(3) 当 时,,解得 ,.
,
不符合题意,舍去.
故该商店销售这种双肩包每天要获得 元的销售利润,销售单价应定为 元.
5. 【答案】
(1)
与 之间的函数表达式为 .
(2) 根据题意得, 当 时, 有最大值,最大值是 .
即这种双肩包销售单价定为 元时,每天的销售利润最大,最大利润是 元.
(3) 当 时,解得,
不符合题意,舍去,
故该商品销售这种双肩包每天要获得 元的销售利润,销售单价应定为 元.
6. 【答案】
(1) .
(2) .
当售价定为 元时,获得最大利润 元.
7. 【答案】
(1) .
(2) 根据题意得 ,
整理得 ,解得 ,.
答:当每件小商品降低 元或 元时,该商店每天能获利 元.
(3) ,
,
当 时, 有最大值,最大值为 .
答:每件小商品销售价为 元时,商店每天销售这种小商品的利润最大,最大利润是 元.
8. 【答案】
(1) 设 ,把 代入得,,解得 .
.
设 ,把 代入得,,解得 .
.
(2) 由题意得,.
解得 ,(舍去).
答:当销售达到 件时,按现行方案月报酬差额达到 元.
(3) 当销售员销售产量达到 件时,
方案一的月报酬为 .
方案二的月报酬为 .
由题意得
解得 .
9. 【答案】
(1) ① ;②
(2) 设安排 名员工,当单价定为 元时,销售量为 万件,所以
(3) 当 时,利润
所以 时,(万元);
当 时,利润
所以 时,(万元).
所以要尽早还清贷款,只有当单价 元时,获得最大月利润 万元,
设该公司 个月后还清贷款,则 .
所以 ,即 为所求.
10. 【答案】
(1) 由图象可知: 与 函数图象的顶点坐标为 ,过点 ,
设: 与 间的函数关系为 .
将点 代入,得:,
与 之间的函数关系式为:.
(2) 令 ,
得:,
解得 ,(舍去).
截止到 月末公司累积利润可达 万元.
(3) 令 ,,
令 ,.
第 个月所获利润为 万元.
11. 【答案】
(1) 根据题意,顶点 的坐标为 ,点 的坐标为 ,
设抛物线的解析式为 ,
把点 代入得:,
解得:,
即所求抛物线的解析式为:.
(2) 由图象可知,高度越高,两排等间的距离越近,
把 代入 得:,
解得:,,
所求最小距离为:,
答:两排灯的水平距离最小是 米.
(3) 根据题意,当 时,
,
能安全通过隧道,
答:这辆特殊货车能安全通过隧道.
12. 【答案】
(1) 设有 间豪华间,由题可得解得经检验 是原方程的根,且符合题意.
则:(元/间).
答:该酒店豪华间有 间,旺季每间价格为 元.
(2) 设上涨 元,日总收入为 ,则 ,
因为 ,
所以抛物线开口向下,
所以当 时,(元).
答:该酒店豪华间价格上涨 元时,豪华间日总收入最高,为 元.
13. 【答案】
(1) 根据题意可得:
与 之间的函数关系为 .
(2) 根据题意可得:
,
当 时, 有最大值, 最大值为 .
答:销售单价定为 元时,每天销售利润最大,最大销售利润 元.
(3) 当 时,可得方程解得 ,
不符合题意,应舍去.
答:该商店销售这种健身球每天想要获得 元的销售利润,销售单价定为 元.
14. 【答案】
(1) 由表格中数据可知,当时间 每增加 天,日销售量相应减少 件,
与 满足一次函数关系.
设 ,将 , 代入,
得: 解得:
与 的函数关系为 .
(2) 设日销售利润为 ,
则 ,
当 时, 有最大值,最大值为 元.
答:第 天时,销售利润最大,最大利润为 元.
15. 【答案】
(1) .
(2) 设每天的利润为 ,
,
,
当时 , 的最大值为 ,
答:该笔筒销售单价定为 元时,每月获取的利润最大,最大利润是 元;
(3) 捐款后销售利润为 ,
则 ,
当 时,,解得 ,,
该笔筒销售单价的范围为 .
16. 【答案】
(1) ,
与 之间的函数表达式是 .
(2)
,
有最大值,当 时,.
当销售单价为 元时,该文具每天的销售利润最大.
(3) 方案 :由题意可知 .
,对称轴是 ,
抛物线开口向下,在对称轴左侧 随 的增大而增大,
当 时, 取最大值.
(元).
方案 :由题意得 ,
,
解得 .
在对称轴右侧 随 的增大而减小,
当 时, 取最大值.
(元),
,
方案 的最大利润更高.
17. 【答案】
(1) 设售价定为 元时,每天的利润为 元,根据题意得:解得:答:售价定为 元或 元时,每天的利润为 元.
(2) 根据题意得:,
即 ,,
故当 时, 元,
答:售价为 元时,利润最大,最大利润是 元.
18. 【答案】
(1) 设培植的盆景比第一期增加 盆,
则第二期盆景有 盆,花卉有 盆.
根据题意,得:
.
.
(2) 根据题意,得:
对称轴 ,
,且 为整数.
当 时, 取得最大值,最大值为 .
答:当 时,第二期培植的盆景与花卉售完后获得的总利润 最大,最大总利润是 元.
19. 【答案】
(1) 设 与 的函数解析式为 ,
由题意得: 解得:
与 的函数解析式为 .
(2) .
,
当 时, 随 的增大而增大.
当 时, 最大,最大利润为 元.
当销售价为 元时,每天的销售利润最大,最大利润为 元.
20. 【答案】
(1) 根据题意,得 ,
即 .
(2) 由题意,得 .
整理,得 .
解这个方程,得 ,.
要使百姓得到实惠,取 .
每台冰箱应降价 元.
(3) 对于 ,
当 时,
.
每台冰箱的售价降价 元时,商场的利润最大,最大利润是 元.
同课章节目录
