人教版九年级上册数学第二十二章 二次函数22.3实际问题与二次函数期末压轴应用题专题训练 (word版含答案)
文档属性
| 名称 | 人教版九年级上册数学第二十二章 二次函数22.3实际问题与二次函数期末压轴应用题专题训练 (word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 258.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 10:13:39 | ||
图片预览




文档简介
人教版九年级上册数学22.3实际问题与二次函数 应用题专题训练
某商场购进一种每件价格为 元的新商品,在商场试销时发现:销售单价 (元/件)与每天销售量 (件)之间满足如图所示的关系.
(1) 求出 与 之间的函数关系式.
(2) 写出每天的利润 与销售单价 之间的函数关系式,并求出售价定为多少时,每天获得的利润最大,最大利润是多少?
某公司投入研发费用 万元( 万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量 销售量),第一年该产品正式投产后,生产成本为 元/件.此产品年销售量 (万件)与售价 (元/件)之间满足函数关系式 .
(1) 求这种产品第一年的利润 (万元)与售价 (元/件)满足的函数关系式;
(2) 该产品第一年的利润为 万元,那么该产品第一年的售价是多少?
(3) 第二年,该公司将第一年的利润 万元( 万元只计入第二年成本)再次投入研发,使产品的生产成本降为 元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过 万件.请计算该公司第二年的利润 至少为多少万元.
在平面直角坐标系中, 为原点,有抛物线 过点 ,矩形 的边 在线段 上(点 在点 的左边),点 , 在抛物线上(点 在点 的左边),设 ,当 时,.
(1) 求抛物线的函数表达式.
(2) 当 为何值时,矩形 的周长有最大值?最大值是多少?
(3) 保持 时的矩形 不动,向右平移抛物线,当平移后的抛物线与矩形的边有两个交点 ,,且直线 平分矩形的面积时,求抛物线平移的距离.
某网商经销一种畅销玩具,每件进价为 元,每月销量 (件)与销售单价 (元)之间的函数关系如图中线段 所示.
(1) 写出每月销量 (件)与销售单价 (元)之间的函数关系式(含 的取值范围) .
(2) 当销售单价为多少元时,该网商每月经销这种玩具能够获得最大销售利润?最大销售利润是多少?(销售利润 售价 进价)
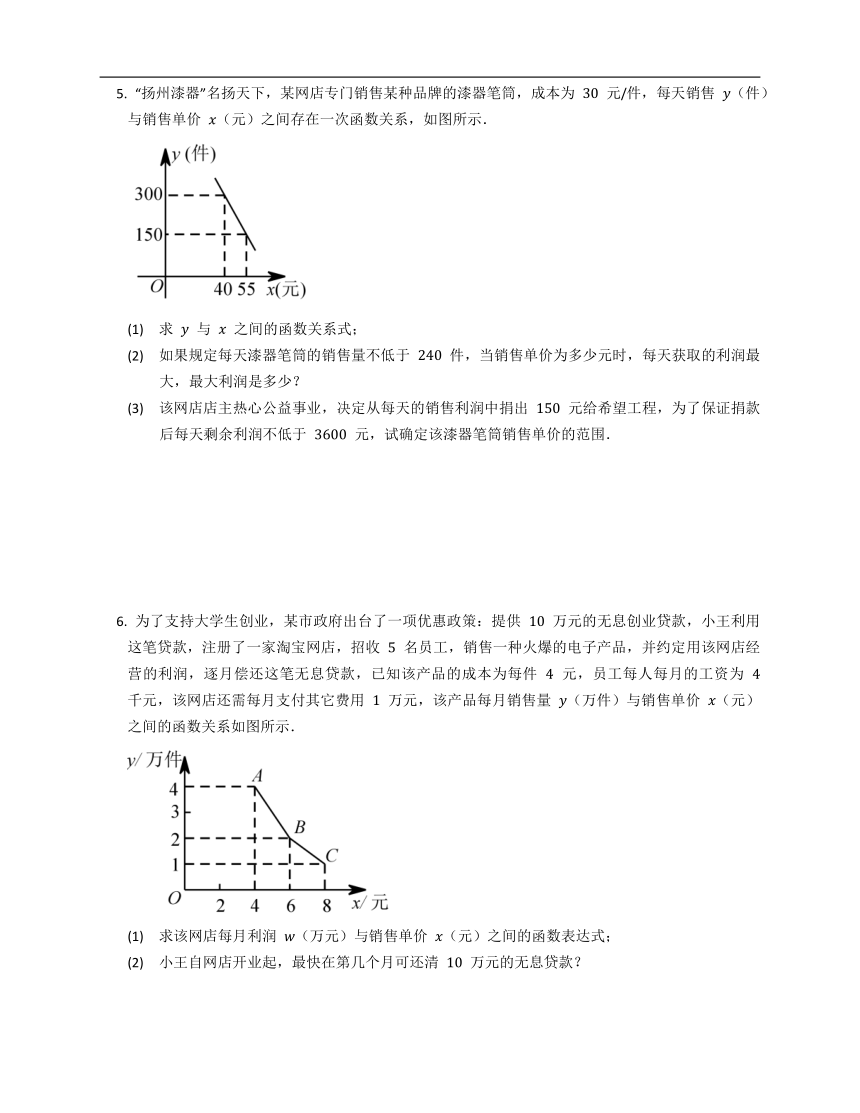
“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为 元/件,每天销售 (件)与销售单价 (元)之间存在一次函数关系,如图所示.
(1) 求 与 之间的函数关系式;
(2) 如果规定每天漆器笔筒的销售量不低于 件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3) 该网店店主热心公益事业,决定从每天的销售利润中捐出 元给希望工程,为了保证捐款后每天剩余利润不低于 元,试确定该漆器笔筒销售单价的范围.
为了支持大学生创业,某市政府出台了一项优惠政策:提供 万元的无息创业贷款,小王利用这笔贷款,注册了一家淘宝网店,招收 名员工,销售一种火爆的电子产品,并约定用该网店经营的利润,逐月偿还这笔无息贷款,已知该产品的成本为每件 元,员工每人每月的工资为 千元,该网店还需每月支付其它费用 万元,该产品每月销售量 (万件)与销售单价 (元)之间的函数关系如图所示.
(1) 求该网店每月利润 (万元)与销售单价 (元)之间的函数表达式;
(2) 小王自网店开业起,最快在第几个月可还清 万元的无息贷款?
甲经销商库存有 套 品牌服装,每套进价 元,每套售价 元,一年内可卖完.现市场上流行 品牌服装,每套进价 元,每套售价 元,但一年内只允许经销商一次性订购 品牌服装,一年内 品牌服装销售无积压.因甲经销商无流动资金,只有低价转让 品牌服装,用转让来的资金购进 品牌服装,并销售.经与乙经销商协商,甲、乙双方达成转让协议,转让价格 (元/套)与转让数量 (套)之间的函数关系式为 .若甲经销商转让 套 品牌服装,一年内所获总利润为 (元).
(1) 求转让后剩余的 品牌服装的销售款 (元)与 (套)之间的函数关系式;
(2) 求 品牌服装的销售款 (元)与 (套)之间的函数关系式;
(3) 求 (元)与 (套)之间的函数关系式,并求 的最大值.
某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资 万元用于该产品的广告促销,已知该产品的本地销售量 (万台)与本地的广告费用 (万元)之间的函数关系满足 .该产品的外地销售量 (万台)与外地广告费用 (万元)之间的函数关系可用如图所示的抛物线和线段 来表示.其中点 为抛物线的顶点.
(1) 结合图象,求出 (万台)与外地广告费用 (万元)之间的函数关系式;
(2) 求该产品的销售总量 (万台)与本地广告费用 (万元)之间的函数关系式;
(3) 如何安排广告费用才能使销售总量最大?
为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件 元,出厂价为每件 元,每月销售量 (件)与销售单价 (元)之间的关系近似满足一次函数:.
(1) 李明在开始创业的第一个月将销售单价定为 元,那么政府这个月为他承担的总差价为多少元?
(2) 设李明获得的利润为 (元),当销售单价定为多少元时,每月可获得最大利润?
(3) 物价部门规定,这种节能灯的销售单价不得高于 元.如果李明想要每月获得的利润不低于 元,那么政府为他承担的总差价最少为多少元?
某商店进了一批服装,每件成本 元,如果按每件 元出售,可销售 件,如果每件提价 元出售,其销量将减少 件.
(1) 求售价为 元时的销售量及销售利润;
(2) 求销售利润 (元)与售价 (元)之间的函数关系,并求售价为多少元时获得最大利润;
(3) 如果商店销售这批服装想获利 元,那么这批服装的定价是多少元?
年 月国际风筝节在婺源县举办,王大伯决定销售一批风筝,经市场调硏:蝙蝠型风筝进价每个为 元,当售价每个为 元时,每天销售量为 个,若售价每提高 元,销售量就会减少 个,请回答下列问题:
(1) 用函数解析式表示蝙蝠型风筝每天销售量 (个)与售价 (元)之间的函数关系 .
(2) 王大伯为了让利给顾客,并同时每天获得 元利润,售价应定为多少?
为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是 元.超市规定每盒售价不得少于 元.根据以往销售经验发现:当售价定为每盒 元时,每天可以卖出 盒,每盒售价每提高 元,每天要少卖出 盒.
(1) 试求出每天的销售量 (盒)与每盒售价 (元)之间的函数关系式.
(2) 当每盒售价定为多少元时,每天销售的利润 (元)最大?最大利润是多少?
(3) 为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于 元.如果超市想要每天获得不低于 元的利润,那么超市每天至少销售粽子多少盒?
如图,隧道的截面由抛物线和长方形构成,长方形的长是 ,宽是 .按照图中所示的直角坐标系,抛物线可以用 表示,且抛物线的点 到墙面 的水平距离为 时,到地面 的距离为 .
(1) 求该抛物线的函数关系式,并计算出拱顶 到地面 的距离;
(2) 一辆货运汽车载一长方体集装箱后高为 ,宽为 ,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3) 在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过 ,那么两排灯的水平距离最小是多少米?
“天天乐”商场销售一种进价为 元/台的台灯,经调查发现,该台灯每天的销售量 (台)与销售单价 (元)满足 ,设销售这种台灯每天的利润为 (元).
(1) 求 与 之间的函数关系式;
(2) 当销售单价定为多少元时,每天的利润最大?最大利润是多少?
(3) 在保证销售量尽可能大的前提下,该商场每天还想获得 元的利润,应该将销售单价定为多少元?
某商场销售一种进价为 元/台的台灯,经调查发现,该台灯每天的销售量 (台),销售单价 (元)满足 ,设销售这种台灯每天的利润为 (元).
(1) 求 与 之间的函数关系式;
(2) 当销售单价定为多少元时.每天的利润最大?最大利润多少?
(3) 在保证销售量尽可能大的前提下.该商场每天还想获得 元的利润,应将销售单价定位为多少元?
某饭店推出一种早点套餐,试销一段时间后发现,每份套餐的成本为 元,若每份售价不超过 元,每天可销售 份;若每份售价超过 元,每提高 元,每天的销售量就减少 份,该店每天固定支出费用为 元(不含套餐成本).为了便于结算,每份套餐的售价取整数,设每份套餐的售价为 元,该店日销售利润为 元.(日销售利润 每天的销售额 套餐成本 每天固定支出)
(1) 求 与 的函数关系式并写出自变量的取值范围.
(2) 该店要想获得最大日销售利润,又要吸引顾客,使每天销售量较大,按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少元?
某企业接到一批粽子生产任务,按要求在 天内完成,约定这批粽子的出厂价为每只 元,为按时完成任务,该企业招收了新工人,设新工人李明第 天生产的粽子数量为 只, 满足下列关系式:.
(1) 李明第几天生产的粽子数量为 只?
(2) 如图,设第 天每只粽子的成本是 元. 与 之间的关系可用图中的函数图象来刻画.若李明第 天创造的利润为 元,求 与 之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?
某商品的进价为每件 元,售价为每件 元,每个月可卖出 件;如果每件商品的售价每上涨 元,则每个月少卖 件(每件售价不能高于 元).设每件商品的售价上涨 元( 为正整数),每个月的销售利润为 元.
(1) 求 与 的函数关系式并直接写出自变量 的取值范围.
(2) 每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3) 每件商品的售价定为多少元时,每个月的利润恰为 元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于 元?
一名大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价为 元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于 元/件,市场调查发现,该产品每天的销售量 (件)与 (元/件)之间的函数关系如图所示.
(1) 求 与 之间的函数关系式,并写出自变量 的取值范围.
(2) 求每天的销售利润 (元)与销售单价 (元/件)之间的函数关系式,并求出每天销售价为多少元时,每天的销售利润最大?最大利润是多少?
某食品厂生产一种半成品食材,成本为 元/千克,每天的产量 (百千克)与销售价格 (元/千克)满足函数关系式 .从市场反馈的信息发现,该食材每天的市场需求量 (百千克)与销售价格 (元/千克)满足一次函数关系,部分数据如表:
已知按物价部门规定销售价格 不低于 元/千克且不高于 元/千克.
(1) 直接写出 与 的函数关系式,并注明自变量 的取值范围;
(2) 当每天的产量小于或等于市场需求量时,这种食材能全部售出;当每天的产量大于市场需求量时,只能售出市场需求的量,而剩余的食材由于保质期短作废弃处理.
①当每天的食材能全部售出时,求 的取值范围;
②求厂家每天获得的利润 (百元)与销售价格 的函数关系式;
(3) 在()的条件下,当 为多少时, 有最大值,并求出最大利润.
答案
一、解答题
1. 【答案】
(1) 设 与 之间的函数关系式 ,
根据题意得 解得
所以 与 之间的函数关系式 .
(2)
而 ,
所以当 时, 有最大值 .
答:售价定位 元时,每天获得的利润最大,最大利润是 元.
2. 【答案】
(1) .
(2) 由题意:解得:答:该产品第一年的售价是 元.
(3) 由题意:,
,
时, 有最小值,最小值 (万元),
答:该公司第二年的利润 至少为 万元.
3. 【答案】
(1) 由题意设抛物线表达式 ,
当 时,,
,
,
,
.
(2) 由抛物线对称性可得 ,
,
当 时,,
,
当 时,矩形 周长有最大值 .
(3) 当 时,点 ,,,,
设矩形 的对角线交点为 ,则 ,
易得当点 , (设 在 下方)分别落在线段 , 上,且直线 过点 时,直线 平分矩形 的面积,
,
线段 平移后得到线段 ,连接 ,则线段 的中点 平移后对应点是 ,连接 .
在 中, 是中位线,
.
故抛物线向右平移的距离为 个单位长度.
4. 【答案】
(1)
(2) 设销售利润为 元,
,
当 时, 取得最大值,.
答:当销售单价为 元时,最大销售利润为 .
5. 【答案】
(1) 略.
(2) 略.
(3) 略.
6. 【答案】
(1) 设直线 的函数表达式为 ,
代入 ,,得 解得
直线 的函数表达式为 .
设直线 的函数表达式为 ,
代入 ,,得 解得
直线 的函数表达式为 .
又 工资及其他费用为 万元,
当 时,
,即 ;
当 时,
,即 .
(2) 当 时,,
当 时, 取得最大值 ;
当 时,,
当 时, 取得最大值 ,
,即第 个月可以还清全部贷款.
7. 【答案】
(1) 甲经销商库存有 套 品牌服装,每套售价 元,转让 套给乙,
.
(2) 转让价格 (元/套)与转让数量 (套)之间的函数关系式 , 品牌服装,每套进价 元,
转让后可以订购 品牌服装 套,
.
(3) 由(1),(2)知,,,
,
当 时, 有最大值,最大值为 元.
8. 【答案】
(1) 由函数图象可知,
当 时,函数图象为抛物线的一部分,
设解析式为 ,
把 代入解析式得,;
当 时,;
与 之间的函数关系式为 .
(2) 本地广告费用为 万元,
外地广告费用为 万元.
时,
;
时,
,
时,
.
(3) 时, 随 的增大而增大.
时, 万台在该区间内最大.
时,,在该区间内 随 增大而增大,
时, 取最大值 万台.
时,,在区间内 随 增大而降低.
当 时,,此时销售总量最大.
外地广告费用为 万元,本地广告费用 万元.
9. 【答案】
(1) 当 时,,(元),
答:政府这个月为他承担的总差价为 元.
(2) 依题意得,
,
当 时, 有最大值 .
答:当销售单价定为 元时,每月可获得最大利润 元.
(3) 由题意得:,
解得:,.
,抛物线开口向下,
结合图象可知:当 时,.
又 ,
当 时,.
设政府每个月为他承担的总差价为 元,
.
,
随 的增大而减小,
当 时, 有最小值 .
答:销售单价定为 元时,政府每个月为他承担的总差价最少为 元.
10. 【答案】
(1) 销售量为 : (件) .
销售利润为: (元).
(2)
所以当销售价为 元时获得最大利润为 元.
(3) 当 时, .
解得 , , 即定价为 元或 元时这批服装可获利 元.
11. 【答案】
(1) 根据题意得:整理得:
(2) 根据题意得:整理得:解得:为让利给顾客,售价应定 元.
答:售价应定 元.
12. 【答案】
(1) 由题意得,.
(2) ,
,,
当 时,,
即当每盒售价定为 元时,每天销售的利润 (元)最大,最大利润是 元.
(3) 由题意,得 ,解得 ,,
抛物线 的开口向下,
当 时,每天销售粽子的利润不低于 元的利润,
又 ,
,
在 中,,
随 的增大而减小,
当 时,,
即超市每天至少销售粽子 盒.
13. 【答案】
(1) 根据题意得 ,,
把 , 代入 得
解得
所以抛物线解析式为 ,
则 ,
所以 ,
所以拱顶 到地面 的距离为 ;
(2) 由题意得货运汽车最外侧与地面 的交点为 或 ,
当 或 时,,
所以这辆货车能安全通过;
(3) 令 ,则 ,解得 ,,
则 ,
所以两排灯的水平距离最小是 .
14. 【答案】
(1) ;
(2) 当 元时,最大利润 元.
(3) 当 时,既能保证销售量最大,又可以每天获得 元的利润.
15. 【答案】
(1)
(2)
当 元时,最大利润 元.
(3) 由题意得,,
即:,
解得:,,
又销售量 随单价 的增大而减小,
所以当 时,既能保证销售量大,又可以每天获得 元的利润.
16. 【答案】
(1) .
(2) 当 时,,
当 时, 元,
当 时,,
当 时,,
当 时,,
要吸引顾客,使每天销售量较大,又要有较高的日纯收入,
每份套餐的售价应定为 元,日纯收入为 元.
17. 【答案】
(1) ,
当 时,,
,
,,
李明第 天生产的粽子数量为 只.
(2) 由图象可得:当 时,,
当 时,设 ,
把点 , 代入得
.
① 时,,
当 时,(元).
② 时,,
,
当 时, 取最大,
为整数,
当 时,(元),
,
综上,第 或 天时,利润最大,为 元,
.
18. 【答案】
(1) (,且 为整数).
(2) 当售价定为每件 或 元,每个月的利润最大,最大的月利润是 元.
(3) 根据题意,得 ,
整理,得 ,解这个方程,得 ,.
当 时,;当 时,.
因此,当每件商品的售价定为 元或 元时,每个月的利润恰为 元.
当 ,且 为整数时,每个月的利润不低于 元.
19. 【答案】
(1) 设 与 的函数解析式为 ,
由题意得:
解得:
与 的函数解析式为 .
(2)
,
当 时, 随 的增大而增大,
当 时, 最大,最大利润为 元,
当销售价为 元时,每天的销售利润最大,最大利润为 元.
20. 【答案】
(1) ,其中 .
(2) ①当每天的半成品食材能全部售出时,有 ,
即 ,解得 ,又 ,
此时 .
②由①可知,当 时,
,
当 时,
即有 .
(3) 当 时, 的对称轴为 ,
当 时,除 的增大而增大,
时有最大值,,
当 时,,
,,
时取最大值,即此时 有最大利润 百元.
某商场购进一种每件价格为 元的新商品,在商场试销时发现:销售单价 (元/件)与每天销售量 (件)之间满足如图所示的关系.
(1) 求出 与 之间的函数关系式.
(2) 写出每天的利润 与销售单价 之间的函数关系式,并求出售价定为多少时,每天获得的利润最大,最大利润是多少?
某公司投入研发费用 万元( 万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量 销售量),第一年该产品正式投产后,生产成本为 元/件.此产品年销售量 (万件)与售价 (元/件)之间满足函数关系式 .
(1) 求这种产品第一年的利润 (万元)与售价 (元/件)满足的函数关系式;
(2) 该产品第一年的利润为 万元,那么该产品第一年的售价是多少?
(3) 第二年,该公司将第一年的利润 万元( 万元只计入第二年成本)再次投入研发,使产品的生产成本降为 元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过 万件.请计算该公司第二年的利润 至少为多少万元.
在平面直角坐标系中, 为原点,有抛物线 过点 ,矩形 的边 在线段 上(点 在点 的左边),点 , 在抛物线上(点 在点 的左边),设 ,当 时,.
(1) 求抛物线的函数表达式.
(2) 当 为何值时,矩形 的周长有最大值?最大值是多少?
(3) 保持 时的矩形 不动,向右平移抛物线,当平移后的抛物线与矩形的边有两个交点 ,,且直线 平分矩形的面积时,求抛物线平移的距离.
某网商经销一种畅销玩具,每件进价为 元,每月销量 (件)与销售单价 (元)之间的函数关系如图中线段 所示.
(1) 写出每月销量 (件)与销售单价 (元)之间的函数关系式(含 的取值范围) .
(2) 当销售单价为多少元时,该网商每月经销这种玩具能够获得最大销售利润?最大销售利润是多少?(销售利润 售价 进价)
“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为 元/件,每天销售 (件)与销售单价 (元)之间存在一次函数关系,如图所示.
(1) 求 与 之间的函数关系式;
(2) 如果规定每天漆器笔筒的销售量不低于 件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3) 该网店店主热心公益事业,决定从每天的销售利润中捐出 元给希望工程,为了保证捐款后每天剩余利润不低于 元,试确定该漆器笔筒销售单价的范围.
为了支持大学生创业,某市政府出台了一项优惠政策:提供 万元的无息创业贷款,小王利用这笔贷款,注册了一家淘宝网店,招收 名员工,销售一种火爆的电子产品,并约定用该网店经营的利润,逐月偿还这笔无息贷款,已知该产品的成本为每件 元,员工每人每月的工资为 千元,该网店还需每月支付其它费用 万元,该产品每月销售量 (万件)与销售单价 (元)之间的函数关系如图所示.
(1) 求该网店每月利润 (万元)与销售单价 (元)之间的函数表达式;
(2) 小王自网店开业起,最快在第几个月可还清 万元的无息贷款?
甲经销商库存有 套 品牌服装,每套进价 元,每套售价 元,一年内可卖完.现市场上流行 品牌服装,每套进价 元,每套售价 元,但一年内只允许经销商一次性订购 品牌服装,一年内 品牌服装销售无积压.因甲经销商无流动资金,只有低价转让 品牌服装,用转让来的资金购进 品牌服装,并销售.经与乙经销商协商,甲、乙双方达成转让协议,转让价格 (元/套)与转让数量 (套)之间的函数关系式为 .若甲经销商转让 套 品牌服装,一年内所获总利润为 (元).
(1) 求转让后剩余的 品牌服装的销售款 (元)与 (套)之间的函数关系式;
(2) 求 品牌服装的销售款 (元)与 (套)之间的函数关系式;
(3) 求 (元)与 (套)之间的函数关系式,并求 的最大值.
某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资 万元用于该产品的广告促销,已知该产品的本地销售量 (万台)与本地的广告费用 (万元)之间的函数关系满足 .该产品的外地销售量 (万台)与外地广告费用 (万元)之间的函数关系可用如图所示的抛物线和线段 来表示.其中点 为抛物线的顶点.
(1) 结合图象,求出 (万台)与外地广告费用 (万元)之间的函数关系式;
(2) 求该产品的销售总量 (万台)与本地广告费用 (万元)之间的函数关系式;
(3) 如何安排广告费用才能使销售总量最大?
为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件 元,出厂价为每件 元,每月销售量 (件)与销售单价 (元)之间的关系近似满足一次函数:.
(1) 李明在开始创业的第一个月将销售单价定为 元,那么政府这个月为他承担的总差价为多少元?
(2) 设李明获得的利润为 (元),当销售单价定为多少元时,每月可获得最大利润?
(3) 物价部门规定,这种节能灯的销售单价不得高于 元.如果李明想要每月获得的利润不低于 元,那么政府为他承担的总差价最少为多少元?
某商店进了一批服装,每件成本 元,如果按每件 元出售,可销售 件,如果每件提价 元出售,其销量将减少 件.
(1) 求售价为 元时的销售量及销售利润;
(2) 求销售利润 (元)与售价 (元)之间的函数关系,并求售价为多少元时获得最大利润;
(3) 如果商店销售这批服装想获利 元,那么这批服装的定价是多少元?
年 月国际风筝节在婺源县举办,王大伯决定销售一批风筝,经市场调硏:蝙蝠型风筝进价每个为 元,当售价每个为 元时,每天销售量为 个,若售价每提高 元,销售量就会减少 个,请回答下列问题:
(1) 用函数解析式表示蝙蝠型风筝每天销售量 (个)与售价 (元)之间的函数关系 .
(2) 王大伯为了让利给顾客,并同时每天获得 元利润,售价应定为多少?
为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是 元.超市规定每盒售价不得少于 元.根据以往销售经验发现:当售价定为每盒 元时,每天可以卖出 盒,每盒售价每提高 元,每天要少卖出 盒.
(1) 试求出每天的销售量 (盒)与每盒售价 (元)之间的函数关系式.
(2) 当每盒售价定为多少元时,每天销售的利润 (元)最大?最大利润是多少?
(3) 为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于 元.如果超市想要每天获得不低于 元的利润,那么超市每天至少销售粽子多少盒?
如图,隧道的截面由抛物线和长方形构成,长方形的长是 ,宽是 .按照图中所示的直角坐标系,抛物线可以用 表示,且抛物线的点 到墙面 的水平距离为 时,到地面 的距离为 .
(1) 求该抛物线的函数关系式,并计算出拱顶 到地面 的距离;
(2) 一辆货运汽车载一长方体集装箱后高为 ,宽为 ,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3) 在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过 ,那么两排灯的水平距离最小是多少米?
“天天乐”商场销售一种进价为 元/台的台灯,经调查发现,该台灯每天的销售量 (台)与销售单价 (元)满足 ,设销售这种台灯每天的利润为 (元).
(1) 求 与 之间的函数关系式;
(2) 当销售单价定为多少元时,每天的利润最大?最大利润是多少?
(3) 在保证销售量尽可能大的前提下,该商场每天还想获得 元的利润,应该将销售单价定为多少元?
某商场销售一种进价为 元/台的台灯,经调查发现,该台灯每天的销售量 (台),销售单价 (元)满足 ,设销售这种台灯每天的利润为 (元).
(1) 求 与 之间的函数关系式;
(2) 当销售单价定为多少元时.每天的利润最大?最大利润多少?
(3) 在保证销售量尽可能大的前提下.该商场每天还想获得 元的利润,应将销售单价定位为多少元?
某饭店推出一种早点套餐,试销一段时间后发现,每份套餐的成本为 元,若每份售价不超过 元,每天可销售 份;若每份售价超过 元,每提高 元,每天的销售量就减少 份,该店每天固定支出费用为 元(不含套餐成本).为了便于结算,每份套餐的售价取整数,设每份套餐的售价为 元,该店日销售利润为 元.(日销售利润 每天的销售额 套餐成本 每天固定支出)
(1) 求 与 的函数关系式并写出自变量的取值范围.
(2) 该店要想获得最大日销售利润,又要吸引顾客,使每天销售量较大,按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少元?
某企业接到一批粽子生产任务,按要求在 天内完成,约定这批粽子的出厂价为每只 元,为按时完成任务,该企业招收了新工人,设新工人李明第 天生产的粽子数量为 只, 满足下列关系式:.
(1) 李明第几天生产的粽子数量为 只?
(2) 如图,设第 天每只粽子的成本是 元. 与 之间的关系可用图中的函数图象来刻画.若李明第 天创造的利润为 元,求 与 之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?
某商品的进价为每件 元,售价为每件 元,每个月可卖出 件;如果每件商品的售价每上涨 元,则每个月少卖 件(每件售价不能高于 元).设每件商品的售价上涨 元( 为正整数),每个月的销售利润为 元.
(1) 求 与 的函数关系式并直接写出自变量 的取值范围.
(2) 每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3) 每件商品的售价定为多少元时,每个月的利润恰为 元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于 元?
一名大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价为 元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于 元/件,市场调查发现,该产品每天的销售量 (件)与 (元/件)之间的函数关系如图所示.
(1) 求 与 之间的函数关系式,并写出自变量 的取值范围.
(2) 求每天的销售利润 (元)与销售单价 (元/件)之间的函数关系式,并求出每天销售价为多少元时,每天的销售利润最大?最大利润是多少?
某食品厂生产一种半成品食材,成本为 元/千克,每天的产量 (百千克)与销售价格 (元/千克)满足函数关系式 .从市场反馈的信息发现,该食材每天的市场需求量 (百千克)与销售价格 (元/千克)满足一次函数关系,部分数据如表:
已知按物价部门规定销售价格 不低于 元/千克且不高于 元/千克.
(1) 直接写出 与 的函数关系式,并注明自变量 的取值范围;
(2) 当每天的产量小于或等于市场需求量时,这种食材能全部售出;当每天的产量大于市场需求量时,只能售出市场需求的量,而剩余的食材由于保质期短作废弃处理.
①当每天的食材能全部售出时,求 的取值范围;
②求厂家每天获得的利润 (百元)与销售价格 的函数关系式;
(3) 在()的条件下,当 为多少时, 有最大值,并求出最大利润.
答案
一、解答题
1. 【答案】
(1) 设 与 之间的函数关系式 ,
根据题意得 解得
所以 与 之间的函数关系式 .
(2)
而 ,
所以当 时, 有最大值 .
答:售价定位 元时,每天获得的利润最大,最大利润是 元.
2. 【答案】
(1) .
(2) 由题意:解得:答:该产品第一年的售价是 元.
(3) 由题意:,
,
时, 有最小值,最小值 (万元),
答:该公司第二年的利润 至少为 万元.
3. 【答案】
(1) 由题意设抛物线表达式 ,
当 时,,
,
,
,
.
(2) 由抛物线对称性可得 ,
,
当 时,,
,
当 时,矩形 周长有最大值 .
(3) 当 时,点 ,,,,
设矩形 的对角线交点为 ,则 ,
易得当点 , (设 在 下方)分别落在线段 , 上,且直线 过点 时,直线 平分矩形 的面积,
,
线段 平移后得到线段 ,连接 ,则线段 的中点 平移后对应点是 ,连接 .
在 中, 是中位线,
.
故抛物线向右平移的距离为 个单位长度.
4. 【答案】
(1)
(2) 设销售利润为 元,
,
当 时, 取得最大值,.
答:当销售单价为 元时,最大销售利润为 .
5. 【答案】
(1) 略.
(2) 略.
(3) 略.
6. 【答案】
(1) 设直线 的函数表达式为 ,
代入 ,,得 解得
直线 的函数表达式为 .
设直线 的函数表达式为 ,
代入 ,,得 解得
直线 的函数表达式为 .
又 工资及其他费用为 万元,
当 时,
,即 ;
当 时,
,即 .
(2) 当 时,,
当 时, 取得最大值 ;
当 时,,
当 时, 取得最大值 ,
,即第 个月可以还清全部贷款.
7. 【答案】
(1) 甲经销商库存有 套 品牌服装,每套售价 元,转让 套给乙,
.
(2) 转让价格 (元/套)与转让数量 (套)之间的函数关系式 , 品牌服装,每套进价 元,
转让后可以订购 品牌服装 套,
.
(3) 由(1),(2)知,,,
,
当 时, 有最大值,最大值为 元.
8. 【答案】
(1) 由函数图象可知,
当 时,函数图象为抛物线的一部分,
设解析式为 ,
把 代入解析式得,;
当 时,;
与 之间的函数关系式为 .
(2) 本地广告费用为 万元,
外地广告费用为 万元.
时,
;
时,
,
时,
.
(3) 时, 随 的增大而增大.
时, 万台在该区间内最大.
时,,在该区间内 随 增大而增大,
时, 取最大值 万台.
时,,在区间内 随 增大而降低.
当 时,,此时销售总量最大.
外地广告费用为 万元,本地广告费用 万元.
9. 【答案】
(1) 当 时,,(元),
答:政府这个月为他承担的总差价为 元.
(2) 依题意得,
,
当 时, 有最大值 .
答:当销售单价定为 元时,每月可获得最大利润 元.
(3) 由题意得:,
解得:,.
,抛物线开口向下,
结合图象可知:当 时,.
又 ,
当 时,.
设政府每个月为他承担的总差价为 元,
.
,
随 的增大而减小,
当 时, 有最小值 .
答:销售单价定为 元时,政府每个月为他承担的总差价最少为 元.
10. 【答案】
(1) 销售量为 : (件) .
销售利润为: (元).
(2)
所以当销售价为 元时获得最大利润为 元.
(3) 当 时, .
解得 , , 即定价为 元或 元时这批服装可获利 元.
11. 【答案】
(1) 根据题意得:整理得:
(2) 根据题意得:整理得:解得:为让利给顾客,售价应定 元.
答:售价应定 元.
12. 【答案】
(1) 由题意得,.
(2) ,
,,
当 时,,
即当每盒售价定为 元时,每天销售的利润 (元)最大,最大利润是 元.
(3) 由题意,得 ,解得 ,,
抛物线 的开口向下,
当 时,每天销售粽子的利润不低于 元的利润,
又 ,
,
在 中,,
随 的增大而减小,
当 时,,
即超市每天至少销售粽子 盒.
13. 【答案】
(1) 根据题意得 ,,
把 , 代入 得
解得
所以抛物线解析式为 ,
则 ,
所以 ,
所以拱顶 到地面 的距离为 ;
(2) 由题意得货运汽车最外侧与地面 的交点为 或 ,
当 或 时,,
所以这辆货车能安全通过;
(3) 令 ,则 ,解得 ,,
则 ,
所以两排灯的水平距离最小是 .
14. 【答案】
(1) ;
(2) 当 元时,最大利润 元.
(3) 当 时,既能保证销售量最大,又可以每天获得 元的利润.
15. 【答案】
(1)
(2)
当 元时,最大利润 元.
(3) 由题意得,,
即:,
解得:,,
又销售量 随单价 的增大而减小,
所以当 时,既能保证销售量大,又可以每天获得 元的利润.
16. 【答案】
(1) .
(2) 当 时,,
当 时, 元,
当 时,,
当 时,,
当 时,,
要吸引顾客,使每天销售量较大,又要有较高的日纯收入,
每份套餐的售价应定为 元,日纯收入为 元.
17. 【答案】
(1) ,
当 时,,
,
,,
李明第 天生产的粽子数量为 只.
(2) 由图象可得:当 时,,
当 时,设 ,
把点 , 代入得
.
① 时,,
当 时,(元).
② 时,,
,
当 时, 取最大,
为整数,
当 时,(元),
,
综上,第 或 天时,利润最大,为 元,
.
18. 【答案】
(1) (,且 为整数).
(2) 当售价定为每件 或 元,每个月的利润最大,最大的月利润是 元.
(3) 根据题意,得 ,
整理,得 ,解这个方程,得 ,.
当 时,;当 时,.
因此,当每件商品的售价定为 元或 元时,每个月的利润恰为 元.
当 ,且 为整数时,每个月的利润不低于 元.
19. 【答案】
(1) 设 与 的函数解析式为 ,
由题意得:
解得:
与 的函数解析式为 .
(2)
,
当 时, 随 的增大而增大,
当 时, 最大,最大利润为 元,
当销售价为 元时,每天的销售利润最大,最大利润为 元.
20. 【答案】
(1) ,其中 .
(2) ①当每天的半成品食材能全部售出时,有 ,
即 ,解得 ,又 ,
此时 .
②由①可知,当 时,
,
当 时,
即有 .
(3) 当 时, 的对称轴为 ,
当 时,除 的增大而增大,
时有最大值,,
当 时,,
,,
时取最大值,即此时 有最大利润 百元.
同课章节目录
