人教版九年级上册数学二十四章24.1.2垂径定理的应用训练(word版含答案)
文档属性
| 名称 | 人教版九年级上册数学二十四章24.1.2垂径定理的应用训练(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 260.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 00:00:00 | ||
图片预览



文档简介
人教版九年级上册数学二十四章垂径定理的应用训练
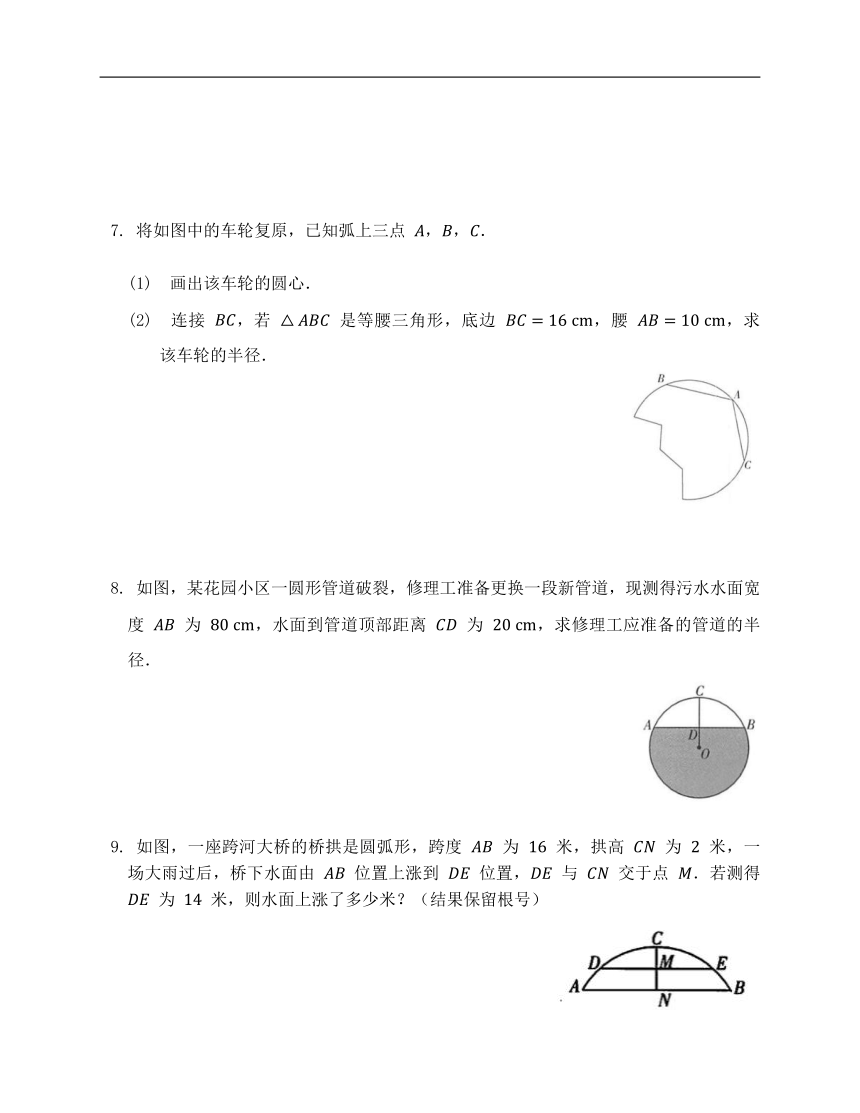
如图:水平放置的圆柱形排水管道内,水面的宽度 ,水面的最大深度为 ,求排水管道截面圆形的半径.
如图,在一座圆弧形拱桥,它的跨度 为 ,拱高 为 ,当洪水泛滥到跨度只有 时,就要采取紧急措施,若某次洪水中,拱顶离水面只有 ,即 时,试通过计算说明是否需要采取紧急措施.
中国的拱桥始建于东汉中后期,已有一千八百余年的历史,如图,一座拱桥在水面上方部分是 ,拱桥在水面上的跨度 为 米,拱桥 与水面的最大距离为 米.
(1) 用直尺和圆规作出 所在圆的圆心 ;
(2) 求拱桥 所在圆的半径.
在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图, 为 的直径,弦 于点 , 寸, 寸,求直径 的长.
请你解答这个问题.
如图,某窗户由矩形和弓形组成,已知弓形的跨度 ,弓高 .现计划安装玻璃,请帮工程师求出弧 所在圆 的半径 .
一些不便于直接测量的圆形孔道的直径可以用如下方法测量.如图,把一个直径为 的小钢球紧贴在孔道边缘,测得钢球顶端离孔道外端的距离为 .求这个孔道的直径 .
将如图中的车轮复原,已知弧上三点 ,,.
(1) 画出该车轮的圆心.
(2) 连接 ,若 是等腰三角形,底边 ,腰 ,求该车轮的半径.
如图,某花园小区一圆形管道破裂,修理工准备更换一段新管道,现测得污水水面宽度 为 ,水面到管道顶部距离 为 ,求修理工应准备的管道的半径.
如图,一座跨河大桥的桥拱是圆弧形,跨度 为 米,拱高 为 米,一场大雨过后,桥下水面由 位置上涨到 位置, 与 交于点 .若测得 为 米,则水面上涨了多少米?(结果保留根号)
如图,两条公路 和 在点 处交汇,.在点 处有一栋居民楼,,如果公路上的汽车行驶时,周围 以内会受噪音影响,那么一汽车在公路 上沿 的方向行驶时,居民楼是否会受到影响?如果这辆汽车的速度是每小时 ,居民楼受影响的时间约为多少?(,精确到 )
筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图①,点 表示筒车的一个盛水桶.如图②,当筒车工作时,盛水桶的运行路径是以轴心 为圆心, 为半径的圆,且圆心在水面上方.若圆被水面截得的弦 长为 ,求筒车工作时,盛水桶在水面以下的最大深度.
一件轮廓为圆形的文物出土后只留下了一块残片,文物学家希望能把此文物进行复原,因此把残片抽象成了一个弓形,如图,经过测量得到弓形高 米,,请你帮助文物学家完成下面两项工作:
(1) 作出此文物轮廓圆心 的位置(尺规作图,保留作图痕迹,不写作法);
(2) 求出弓形所在圆的半径.
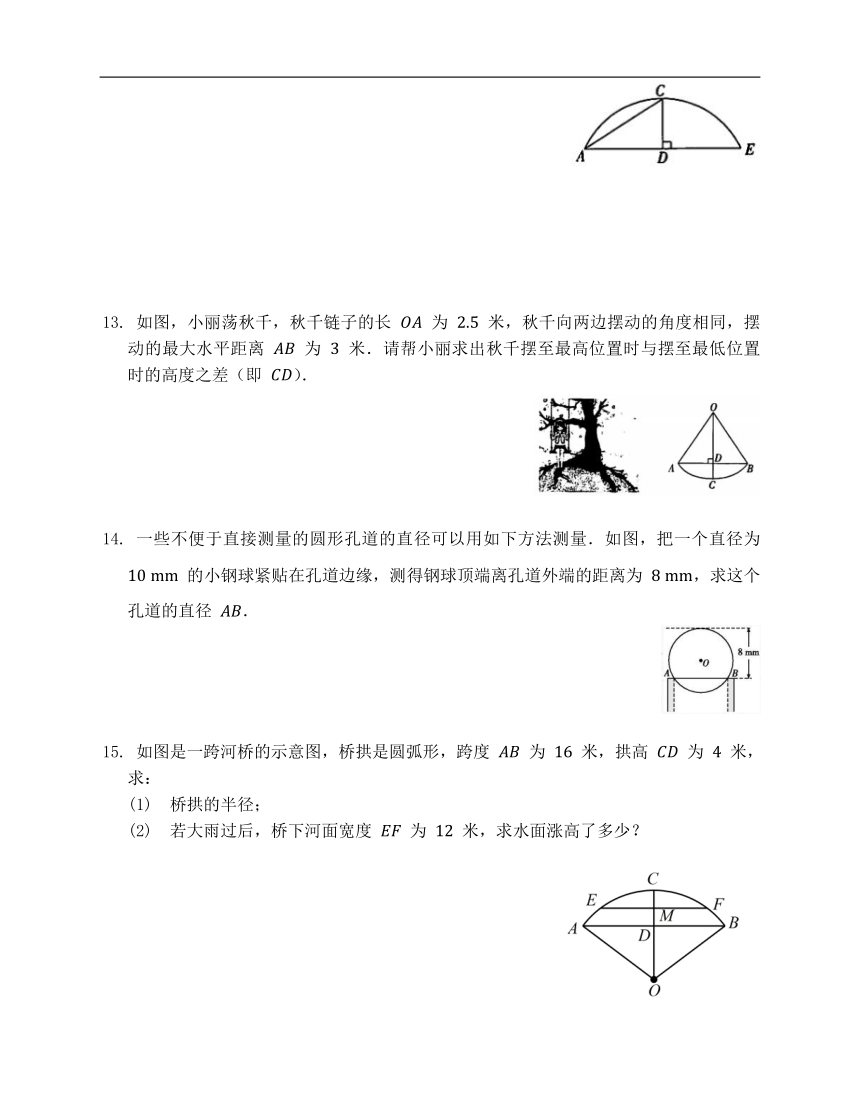
如图,小丽荡秋千,秋千链子的长 为 米,秋千向两边摆动的角度相同,摆动的最大水平距离 为 米.请帮小丽求出秋千摆至最高位置时与摆至最低位置时的高度之差(即 ).
一些不便于直接测量的圆形孔道的直径可以用如下方法测量.如图,把一个直径为 的小钢球紧贴在孔道边缘,测得钢球顶端离孔道外端的距离为 ,求这个孔道的直径 .
如图是一跨河桥的示意图,桥拱是圆弧形,跨度 为 米,拱高 为 米,求:
(1) 桥拱的半径;
(2) 若大雨过后,桥下河面宽度 为 米,求水面涨高了多少?
“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”.这是《九章算术》中的问题,用数学语言可表述为:如图, 为 的直径,弦 于点 , 寸, 寸,求直径 的长.
如图是一个半圆形桥洞截面示意图,圆心为 ,直径 是河底线,弦 是水位线,,且 于点 .已测得 .
(1) 求半径 ;
(2) 根据需要,水面要以每小时 的速度下降,则经过多长时间才能将水排干?
如图, 城气象台测得台风中心在 城正西方向 的 处,以 的速度向北偏东 的 方向移动,距台风中心 的范围内将受到台风影响.
(1) 城是否受到这次台风的影响?为什么?
(2) 若 城受到台风影响,那么 城遭受这次台风影响的时间有多长?
如图,某地有一圆弧形拱桥,桥下水面宽为 ,拱顶高出水面 .现有一艘宽 、船舱顶部为长方形并高出水面 的货船要经过这里,此货船能顺利通过这座拱桥吗?
如图,圆柱形水管内原有积水的水平面宽 ,水深 .若水面上升 ,则此时水面宽 为多少?
答案
一、解答题
1. 【答案】 .
2. 【答案】设圆弧所在圆的圆心为 ,连接 ,.
设半径为 米,则 ,
由垂径定理可知 ,,
米,
米,且 米,
在 中,由勾股定理可得 ,
即 ,解得 ,
(米),
在 中,
由勾股定理可得 (米),
米 米,
不需要采取紧急措施.
3. 【答案】
(1) 如图所示,点 即为所求;
(2) 如图,取 的中点 ,连接 交 于点 ,连接 ,
则 ,且 ,
由题意得,,
设圆的半径为 ,
在 中,,
即 ,
解得 .
即拱桥 所在圆的半径为 .
4. 【答案】如图所示,连接 .
弦 , 为圆 的直径,
为 的中点,
又 寸,
寸,
设 寸,则 寸, 寸,
由勾股定理得:,
即 ,解得:,
寸,即直径 的长为 寸.
5. 【答案】 弓形的跨度 ,
,
,
所在圆 的半径为 ,弓形的高 ,
,,
在 中,,
即 ,解得 .
答: 所在圆 的半径为 .
6. 【答案】如图,过点 作 ,交 于点 ,交 于点 ,连接 .
由题意可知,,.
.
.
.
答:这个孔道的直径为 .
7. 【答案】
(1) 如图 ,分别作弦 和 的垂直平分线,它们交于点 ,则交点 即为所求作的圆心.
(2) 如图 ,连接 ,, 与 交于点 ,
由题意知 ,
,则 垂直平分 .
,
.
在 中,,
.
设该车轮的半径为 ,在 中,,
,解得 ,
该车轮的半径为 .
8. 【答案】如答图,连接 .
由题意得 ,,,,
.
设 ,
则 .
在 中,,
即 .
解得 .
修理工应准备的管道的半径为 .
9. 【答案】如图,延长 至点 ,使得 ,则点 即为圆心,连接 .
由题意,得 ,
.
同理可得 .
设圆弧形拱桥所在圆的半径为 米,
则 米.
在 中,,
即 .
解得 .
在 中,,
.
.
答:水面上涨了 米.
10. 【答案】过点 作 于点 .
,
,即居民楼受影响.
以 为圆心, 为半径的 与 交于点 ,,
则线段 为居民楼受影响的路段.
在 中,
.
于点 ,
.
汽车速度为 ,即 ,
.
居民楼受噪音影响的时间约为 .
11. 【答案】如图,作 于 ,交 于点 ,
则 .
,
.
在 中,,
.
.
筒车工作时,盛水桶在水面以下的最大深度为 .
12. 【答案】
(1) 如图所示,点 即为所求作的点.
(2) 如图,连接 .
在 中,,
米,,
米.
答:此弓形所在圆的半径为 米
13. 【答案】 ,
米.
由勾股定理得 米.
米.
秋千摆至最高位置时与摆至最低位置时的高度之差为 米.
14. 【答案】连接 ,过点 作 于点 ,则 .
因为钢珠的直径是 ,
所以钢珠的半径是 .
因为钢珠顶端离零件表面的距离为 ,
所以 .
在 中,
因为 ,
所以 .
则这个孔道的直径 为 .
15. 【答案】
(1) 已知桥拱的跨度 (米),拱高 (米),
(米).
利用勾股定理可得 ,
解得 (米).
故桥拱的半径为 米.
(2) 如图,当河水上涨到 位置时,
(米),,
,
(米).
连接 ,
则 (米),
(米).
又 (米),
(米),即水面涨高了 米.
16. 【答案】连接 ,如图所示.
设直径 的长为 ,则半径 ,
为 的直径,弦 于 , 寸,
寸,
连接 ,则 寸,
根据勾股定理得 ,
解得 ,
直径 的长为 (寸).
17. 【答案】
(1) 于点 ,,
.
在 中,
,
,
故半径 为 .
(2) ,
(小时).
故经过 小时才能将水排干.
18. 【答案】
(1) 城会受到这次台风的影响.
理由:过点 作 ,垂足为 ,
在 中,因为 ,
所以 .
又因为台风影响范围半径为 ,
所以 市会受到这次台风的影响.
(2) .
19. 【答案】用 表示桥拱, 所在圆的圆心为 ,半径为 ,经过圆心 作弦 的垂线 ,点 为垂足,与 相交于点 .根据垂径定理, 是 的中点, 是 的中点, 就是拱高.
由题设得 ,,,
,
.
在 中,由勾股定理,得 .
即 ,解得 .
在 中,由勾股定理,得 ,
,
此货船能顺利通过这座拱桥.
20. 【答案】连接 ,,
因为由题意知:,,,,
所以 ,
在 中,由勾股定理得:,
,
解得:,
则 ,
因为在 中,由勾股定理得:,
所以 ,
所以 ,
因为 , 过圆心 ,
所以 .
如图:水平放置的圆柱形排水管道内,水面的宽度 ,水面的最大深度为 ,求排水管道截面圆形的半径.
如图,在一座圆弧形拱桥,它的跨度 为 ,拱高 为 ,当洪水泛滥到跨度只有 时,就要采取紧急措施,若某次洪水中,拱顶离水面只有 ,即 时,试通过计算说明是否需要采取紧急措施.
中国的拱桥始建于东汉中后期,已有一千八百余年的历史,如图,一座拱桥在水面上方部分是 ,拱桥在水面上的跨度 为 米,拱桥 与水面的最大距离为 米.
(1) 用直尺和圆规作出 所在圆的圆心 ;
(2) 求拱桥 所在圆的半径.
在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图, 为 的直径,弦 于点 , 寸, 寸,求直径 的长.
请你解答这个问题.
如图,某窗户由矩形和弓形组成,已知弓形的跨度 ,弓高 .现计划安装玻璃,请帮工程师求出弧 所在圆 的半径 .
一些不便于直接测量的圆形孔道的直径可以用如下方法测量.如图,把一个直径为 的小钢球紧贴在孔道边缘,测得钢球顶端离孔道外端的距离为 .求这个孔道的直径 .
将如图中的车轮复原,已知弧上三点 ,,.
(1) 画出该车轮的圆心.
(2) 连接 ,若 是等腰三角形,底边 ,腰 ,求该车轮的半径.
如图,某花园小区一圆形管道破裂,修理工准备更换一段新管道,现测得污水水面宽度 为 ,水面到管道顶部距离 为 ,求修理工应准备的管道的半径.
如图,一座跨河大桥的桥拱是圆弧形,跨度 为 米,拱高 为 米,一场大雨过后,桥下水面由 位置上涨到 位置, 与 交于点 .若测得 为 米,则水面上涨了多少米?(结果保留根号)
如图,两条公路 和 在点 处交汇,.在点 处有一栋居民楼,,如果公路上的汽车行驶时,周围 以内会受噪音影响,那么一汽车在公路 上沿 的方向行驶时,居民楼是否会受到影响?如果这辆汽车的速度是每小时 ,居民楼受影响的时间约为多少?(,精确到 )
筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图①,点 表示筒车的一个盛水桶.如图②,当筒车工作时,盛水桶的运行路径是以轴心 为圆心, 为半径的圆,且圆心在水面上方.若圆被水面截得的弦 长为 ,求筒车工作时,盛水桶在水面以下的最大深度.
一件轮廓为圆形的文物出土后只留下了一块残片,文物学家希望能把此文物进行复原,因此把残片抽象成了一个弓形,如图,经过测量得到弓形高 米,,请你帮助文物学家完成下面两项工作:
(1) 作出此文物轮廓圆心 的位置(尺规作图,保留作图痕迹,不写作法);
(2) 求出弓形所在圆的半径.
如图,小丽荡秋千,秋千链子的长 为 米,秋千向两边摆动的角度相同,摆动的最大水平距离 为 米.请帮小丽求出秋千摆至最高位置时与摆至最低位置时的高度之差(即 ).
一些不便于直接测量的圆形孔道的直径可以用如下方法测量.如图,把一个直径为 的小钢球紧贴在孔道边缘,测得钢球顶端离孔道外端的距离为 ,求这个孔道的直径 .
如图是一跨河桥的示意图,桥拱是圆弧形,跨度 为 米,拱高 为 米,求:
(1) 桥拱的半径;
(2) 若大雨过后,桥下河面宽度 为 米,求水面涨高了多少?
“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”.这是《九章算术》中的问题,用数学语言可表述为:如图, 为 的直径,弦 于点 , 寸, 寸,求直径 的长.
如图是一个半圆形桥洞截面示意图,圆心为 ,直径 是河底线,弦 是水位线,,且 于点 .已测得 .
(1) 求半径 ;
(2) 根据需要,水面要以每小时 的速度下降,则经过多长时间才能将水排干?
如图, 城气象台测得台风中心在 城正西方向 的 处,以 的速度向北偏东 的 方向移动,距台风中心 的范围内将受到台风影响.
(1) 城是否受到这次台风的影响?为什么?
(2) 若 城受到台风影响,那么 城遭受这次台风影响的时间有多长?
如图,某地有一圆弧形拱桥,桥下水面宽为 ,拱顶高出水面 .现有一艘宽 、船舱顶部为长方形并高出水面 的货船要经过这里,此货船能顺利通过这座拱桥吗?
如图,圆柱形水管内原有积水的水平面宽 ,水深 .若水面上升 ,则此时水面宽 为多少?
答案
一、解答题
1. 【答案】 .
2. 【答案】设圆弧所在圆的圆心为 ,连接 ,.
设半径为 米,则 ,
由垂径定理可知 ,,
米,
米,且 米,
在 中,由勾股定理可得 ,
即 ,解得 ,
(米),
在 中,
由勾股定理可得 (米),
米 米,
不需要采取紧急措施.
3. 【答案】
(1) 如图所示,点 即为所求;
(2) 如图,取 的中点 ,连接 交 于点 ,连接 ,
则 ,且 ,
由题意得,,
设圆的半径为 ,
在 中,,
即 ,
解得 .
即拱桥 所在圆的半径为 .
4. 【答案】如图所示,连接 .
弦 , 为圆 的直径,
为 的中点,
又 寸,
寸,
设 寸,则 寸, 寸,
由勾股定理得:,
即 ,解得:,
寸,即直径 的长为 寸.
5. 【答案】 弓形的跨度 ,
,
,
所在圆 的半径为 ,弓形的高 ,
,,
在 中,,
即 ,解得 .
答: 所在圆 的半径为 .
6. 【答案】如图,过点 作 ,交 于点 ,交 于点 ,连接 .
由题意可知,,.
.
.
.
答:这个孔道的直径为 .
7. 【答案】
(1) 如图 ,分别作弦 和 的垂直平分线,它们交于点 ,则交点 即为所求作的圆心.
(2) 如图 ,连接 ,, 与 交于点 ,
由题意知 ,
,则 垂直平分 .
,
.
在 中,,
.
设该车轮的半径为 ,在 中,,
,解得 ,
该车轮的半径为 .
8. 【答案】如答图,连接 .
由题意得 ,,,,
.
设 ,
则 .
在 中,,
即 .
解得 .
修理工应准备的管道的半径为 .
9. 【答案】如图,延长 至点 ,使得 ,则点 即为圆心,连接 .
由题意,得 ,
.
同理可得 .
设圆弧形拱桥所在圆的半径为 米,
则 米.
在 中,,
即 .
解得 .
在 中,,
.
.
答:水面上涨了 米.
10. 【答案】过点 作 于点 .
,
,即居民楼受影响.
以 为圆心, 为半径的 与 交于点 ,,
则线段 为居民楼受影响的路段.
在 中,
.
于点 ,
.
汽车速度为 ,即 ,
.
居民楼受噪音影响的时间约为 .
11. 【答案】如图,作 于 ,交 于点 ,
则 .
,
.
在 中,,
.
.
筒车工作时,盛水桶在水面以下的最大深度为 .
12. 【答案】
(1) 如图所示,点 即为所求作的点.
(2) 如图,连接 .
在 中,,
米,,
米.
答:此弓形所在圆的半径为 米
13. 【答案】 ,
米.
由勾股定理得 米.
米.
秋千摆至最高位置时与摆至最低位置时的高度之差为 米.
14. 【答案】连接 ,过点 作 于点 ,则 .
因为钢珠的直径是 ,
所以钢珠的半径是 .
因为钢珠顶端离零件表面的距离为 ,
所以 .
在 中,
因为 ,
所以 .
则这个孔道的直径 为 .
15. 【答案】
(1) 已知桥拱的跨度 (米),拱高 (米),
(米).
利用勾股定理可得 ,
解得 (米).
故桥拱的半径为 米.
(2) 如图,当河水上涨到 位置时,
(米),,
,
(米).
连接 ,
则 (米),
(米).
又 (米),
(米),即水面涨高了 米.
16. 【答案】连接 ,如图所示.
设直径 的长为 ,则半径 ,
为 的直径,弦 于 , 寸,
寸,
连接 ,则 寸,
根据勾股定理得 ,
解得 ,
直径 的长为 (寸).
17. 【答案】
(1) 于点 ,,
.
在 中,
,
,
故半径 为 .
(2) ,
(小时).
故经过 小时才能将水排干.
18. 【答案】
(1) 城会受到这次台风的影响.
理由:过点 作 ,垂足为 ,
在 中,因为 ,
所以 .
又因为台风影响范围半径为 ,
所以 市会受到这次台风的影响.
(2) .
19. 【答案】用 表示桥拱, 所在圆的圆心为 ,半径为 ,经过圆心 作弦 的垂线 ,点 为垂足,与 相交于点 .根据垂径定理, 是 的中点, 是 的中点, 就是拱高.
由题设得 ,,,
,
.
在 中,由勾股定理,得 .
即 ,解得 .
在 中,由勾股定理,得 ,
,
此货船能顺利通过这座拱桥.
20. 【答案】连接 ,,
因为由题意知:,,,,
所以 ,
在 中,由勾股定理得:,
,
解得:,
则 ,
因为在 中,由勾股定理得:,
所以 ,
所以 ,
因为 , 过圆心 ,
所以 .
同课章节目录
