分类思想在坐标系中的应用

(共12张PPT)
分类思想在坐标系中的应用
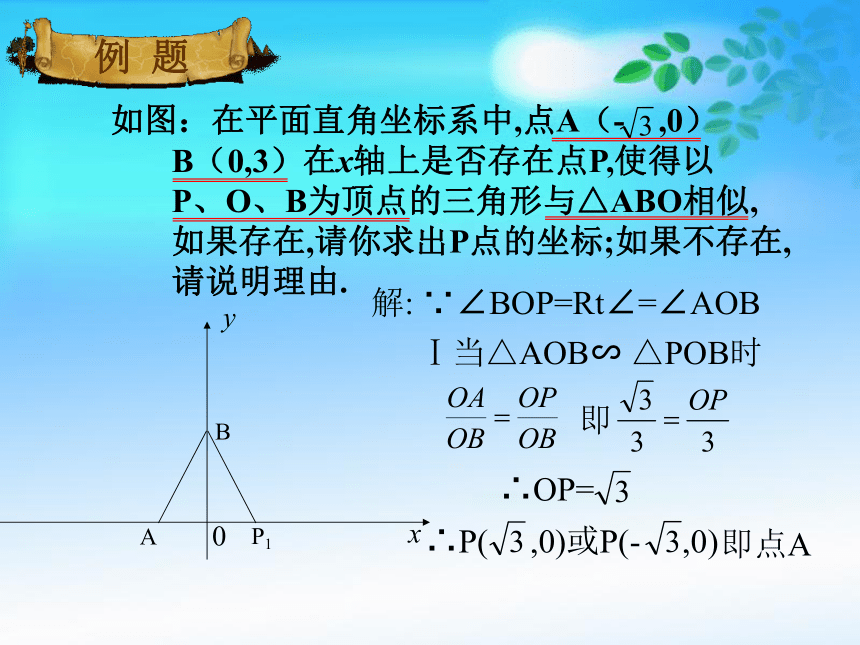
如图：在平面直角坐标系中,点A（- ,0） B（0,3）在x轴上是否存在点P,使得以 P、O、B为顶点的三角形与△ABO相似, 如果存在,请你求出P点的坐标;如果不存在, 请说明理由.
y
x
A
0
B
P1
解: ∵∠BOP=Rt∠=∠AOB
Ⅰ当△AOB∽ △POB时
即
∴P( ,0)或P(- ,0)
∴OP=
即点A
例 题
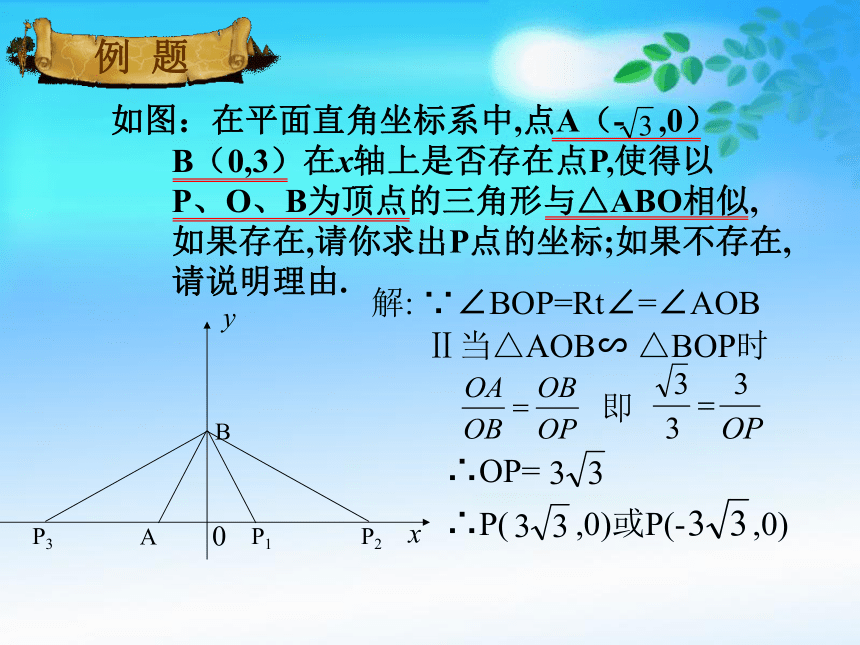
如图：在平面直角坐标系中,点A（- ,0） B（0,3）在x轴上是否存在点P,使得以 P、O、B为顶点的三角形与△ABO相似, 如果存在,请你求出P点的坐标;如果不存在, 请说明理由.
y
x
A
0
B
P1
P2
P3
Ⅱ当△AOB∽ △BOP时
∴OP=
即
解: ∵∠BOP=Rt∠=∠AOB
∴P( ,0)或P(- ,0)
例 题
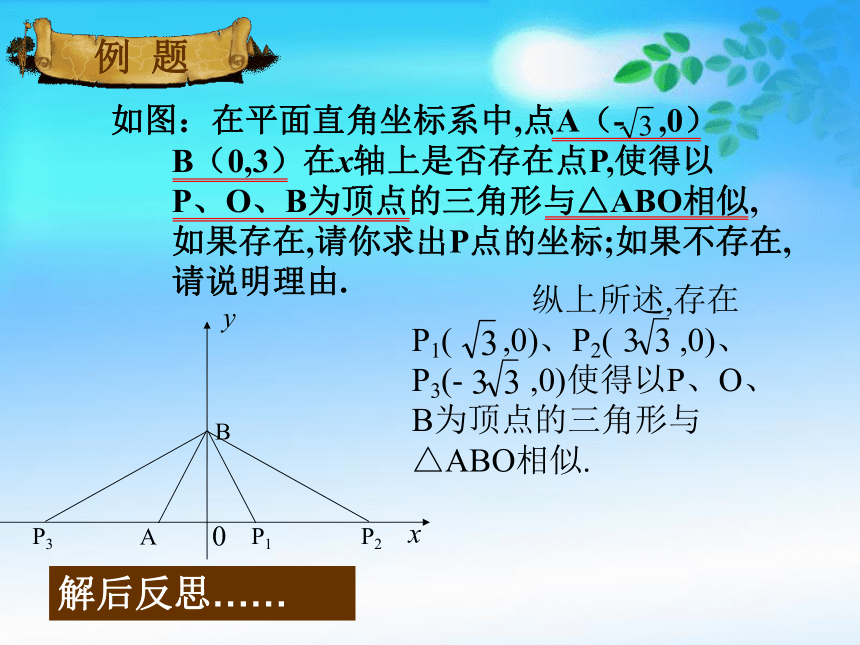
如图：在平面直角坐标系中,点A（- ,0） B（0,3）在x轴上是否存在点P,使得以 P、O、B为顶点的三角形与△ABO相似, 如果存在,请你求出P点的坐标;如果不存在, 请说明理由.
y
x
A
0
B
P1
P2
P3
纵上所述,存在P1( ,0)、P2( ,0)、P3(- ,0)使得以P、O、B为顶点的三角形与△ABO相似.
解后反思……
例 题
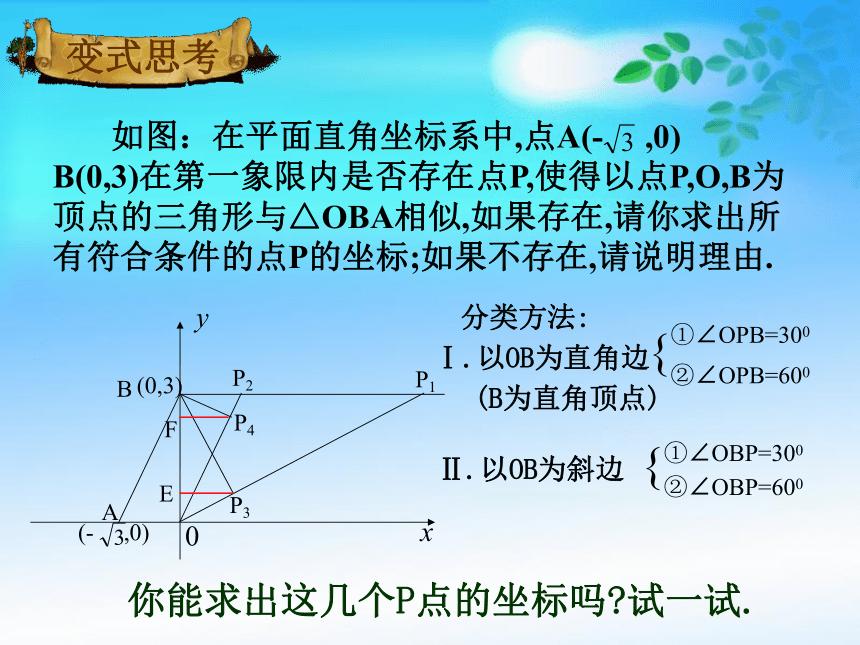
如图：在平面直角坐标系中,点A(- ,0)
B(0,3)在第一象限内是否存在点P,使得以点P,O,B为顶点的三角形与△OBA相似,如果存在,请你求出所有符合条件的点P的坐标;如果不存在,请说明理由.
(0,3)
(- ,0)
y
x
A
0
B
分类方法:
Ⅰ.以OB为直角边
(B为直角顶点)
Ⅱ.以OB为斜边
①∠OBP=300
②∠OBP=600
①∠OPB=300
②∠OPB=600
P1
P2
P3
P4
{
{
你能求出这几个P点的坐标吗 试一试.
E
F
变式思考
如图,点A（-4,0）B（0,3）试在x轴上确定点P,使△PAB为等腰三角形.你能求出这样的点P的坐标吗 与同伴合作试一试.
y
x
A(-4,0)
0
B(0,3)
合作探究
1.分类讨论
2.点的坐标 线段的长(数形结合)
确定分类标准
不重不漏
回顾 小结
㈠写一篇学习体会(字数不限)
㈡1.已知x轴上有点A(-2,0)，B(4,0)点P为直线y= x+2上的一点,它的横坐标为m,当m为何值时, △ABP为直角三角形.
2.如图,在平面直角坐标系中,Rt△ABC斜边AB在x轴上,顶点C在y轴的负半轴上,tg∠ABC= ,点P在线段OC上,且PO，PC的长（PO(1)求P点坐标; (2)求AP的长;
(3)在x轴上是否存在点Q,使以
点A、C、P、Q为顶点的四
边形是梯形 若存在,请直接
写出直线PQ的解析式;若不
存在,请说明理由.
A
B
C
O
x
y
作 业
谢 谢 指 导 ！
如图：点M是直线y=2x+3上的动点,过点M作MN垂直x轴于点N,问:y轴上是否存在点P,使得以M,N,P为顶点的三角形为等腰直角三角形.如果存在,请你求出相应的点P和点M的坐标;如果不存在,请说明理由.
y=2x+3
y
x
0
M
N
合作 探究
如图：在坐标平面内是否存在点P,使△PAB 与△AOB相似,若存在,请说出这样的P点共有几个？若不存在,请说明理由.
合作探究
(0,3)
(- ,0)
y
x
A
0
B
分类方法:
Ⅰ.以AB为直角边
Ⅱ.以AB为斜边
① B为直角顶点
② A为直角顶点
{