2021-2022学年湘教版九年级数学上册4.4解直角三角形的应用 解答专题训练(word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版九年级数学上册4.4解直角三角形的应用 解答专题训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 688.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 00:00:00 | ||
图片预览


文档简介
2021-2022学年湘教版九年级数学上册《4.4解直角三角形的应用》解答专题训练(附答案)
1.某校数学兴趣小组学完“三角函数的应用”后,在校园内利用三角尺测量教学楼AB的高度,如图,小明同学站在点D处,将含45°角三角尺的一条直角边水平放置,此时三角尺的倾斜边刚好落在视线CA上,沿教学楼向前走8米到达点F处,将含30°角三角尺的短直角边水平放置,此时三角尺的斜边也刚好落在视线EA上,已知小明眼睛到地面的距离为1.6米,求教学楼AB的高度.(点D,F,B在同一水平线上,结果保留根号)
2.如图,小明在笔直的河岸MN上的点A处,以正对岸明显的标志点O为参照点,设计出测量河宽OA的方案,绘制了相应的示意图,并用测角仪、卷尺及标杆测得一些数据如下:
(1)请你结合示意图,简述选择标志点O为参照点之后的测量过程;
(2)按照方案,求河宽OA.(参考数据:tan75°≈,tan56°≈)
3.水坝的横截面是梯形ABCD,现测得坝顶DC=4m,坡面AD的坡度i为1:1,坡面BC的坡角β为60°,坝高3m,(≈1.732)求:
(1)坝底AB的长(精确到0.1);
(2)水利部门为了加固水坝,在保持坝顶CD不变的情况下降低AD的坡度(如图),使新坡面DE的坡度i为1:,原水坝底部正前方2.5m处有一千年古树,此加固工程对古树是否有影响?请说明理由.
4.如图,平地上两栋建筑物AB和CD相距30m,在建筑物AB的顶部测得建筑物CD底部的俯角为26.6°,测得建筑物CD顶部的仰角为45°.求建筑物CD的高度.(参考数据:sin16.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50)
5.图①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图,托板长AB=115mm,支撑板长CD=70mm,板AB固定在支撑板顶点C处,且CB=35mm,托板AB可绕点C转动,支撑板CD可绕点D转动.
(1)当∠CDE=60°时,
①求点C到直线DE的距离(计算结果保留根号);
②若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);
(2)为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在直线DE上即可,则CD旋转的角度为 .(直接写出结果)
(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,≈1.7)
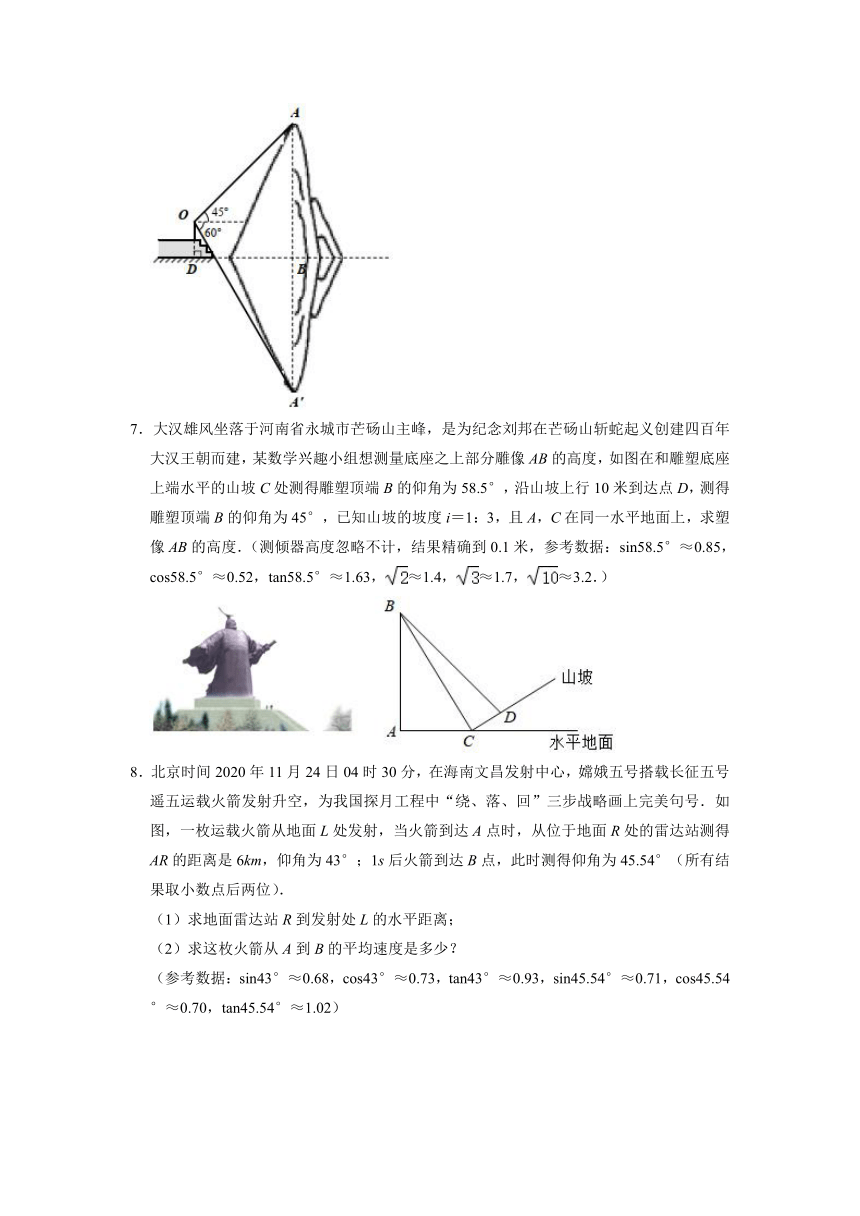
6.小宸想利用测量知识测算湖中小山的高度.他站在湖边看台上,清晰地看到小山倒映在平静的湖水中,如图所示,他在点O处测得小山顶端的仰角为45°,小山顶端A在水中倒影A′的俯角为60°.已知:点O到湖面的距离OD=3m,OD⊥DB,AB⊥DB,A、B、A′三点共线,A'B=AB,求小山的高度AB.(光线的折射忽略不计;结果保留根号)
7.大汉雄风坐落于河南省永城市芒砀山主峰,是为纪念刘邦在芒砀山斩蛇起义创建四百年大汉王朝而建,某数学兴趣小组想测量底座之上部分雕像AB的高度,如图在和雕塑底座上端水平的山坡C处测得雕塑顶端B的仰角为58.5°,沿山坡上行10米到达点D,测得雕塑顶端B的仰角为45°,已知山坡的坡度i=1:3,且A,C在同一水平地面上,求塑像AB的高度.(测倾器高度忽略不计,结果精确到0.1米,参考数据:sin58.5°≈0.85,cos58.5°≈0.52,tan58.5°≈1.63,≈1.4,≈1.7,≈3.2.)
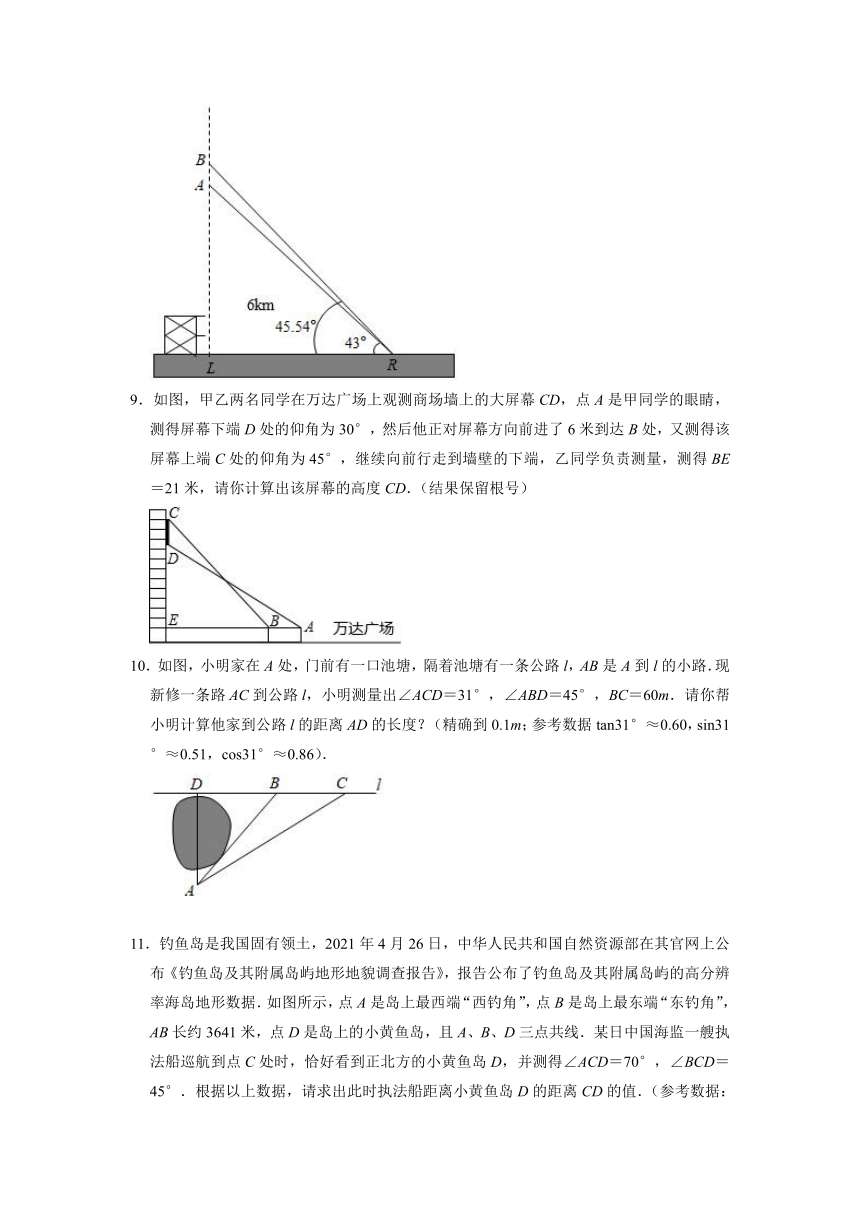
8.北京时间2020年11月24日04时30分,在海南文昌发射中心,嫦娥五号搭载长征五号遥五运载火箭发射升空,为我国探月工程中“绕、落、回”三步战略画上完美句号.如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站测得AR的距离是6km,仰角为43°;1s后火箭到达B点,此时测得仰角为45.54°(所有结果取小数点后两位).
(1)求地面雷达站R到发射处L的水平距离;
(2)求这枚火箭从A到B的平均速度是多少?
(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93,sin45.54°≈0.71,cos45.54°≈0.70,tan45.54°≈1.02)
9.如图,甲乙两名同学在万达广场上观测商场墙上的大屏幕CD,点A是甲同学的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6米到达B处,又测得该屏幕上端C处的仰角为45°,继续向前行走到墙壁的下端,乙同学负责测量,测得BE=21米,请你计算出该屏幕的高度CD.(结果保留根号)
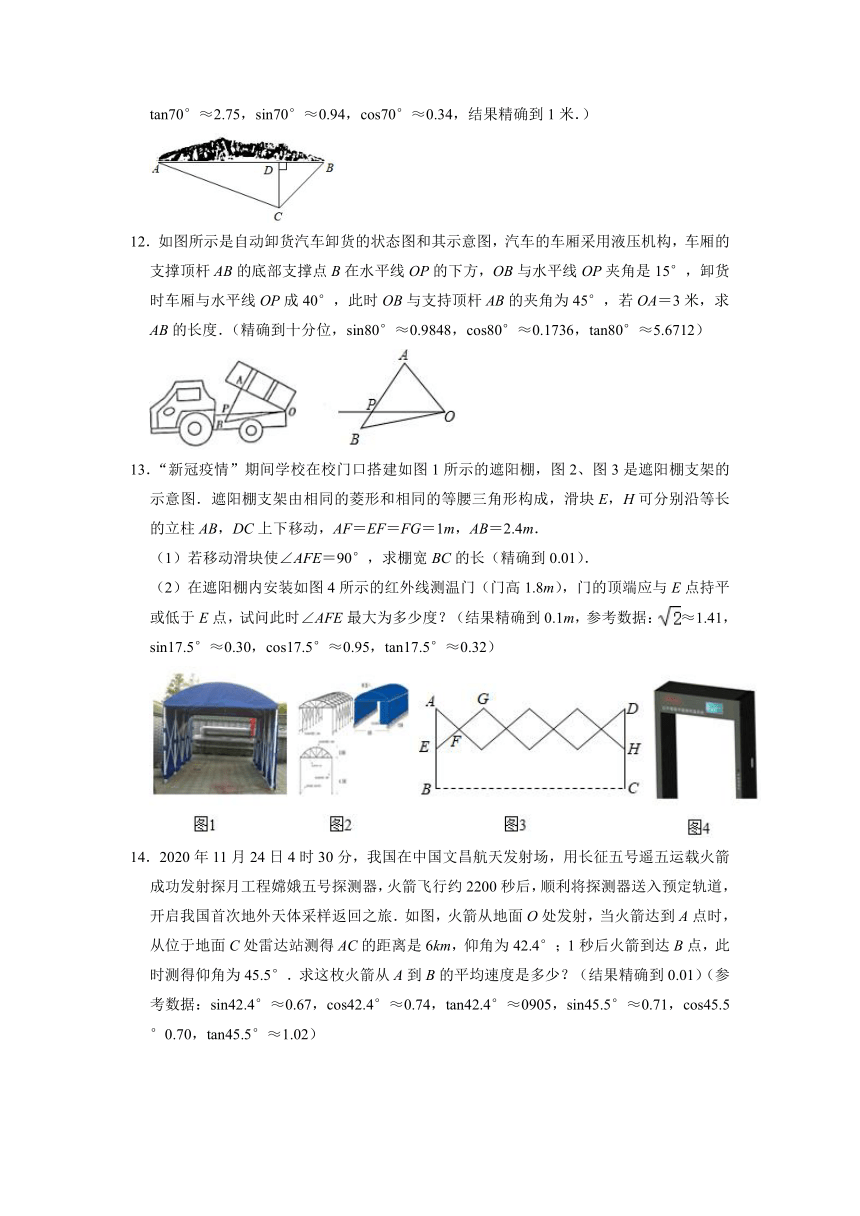
10.如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l,小明测量出∠ACD=31°,∠ABD=45°,BC=60m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
11.钓鱼岛是我国固有领土,2021年4月26日,中华人民共和国自然资源部在其官网上公布《钓鱼岛及其附属岛屿地形地貌调查报告》,报告公布了钓鱼岛及其附属岛屿的高分辨率海岛地形数据.如图所示,点A是岛上最西端“西钓角”,点B是岛上最东端“东钓角”,AB长约3641米,点D是岛上的小黄鱼岛,且A、B、D三点共线.某日中国海监一艘执法船巡航到点C处时,恰好看到正北方的小黄鱼岛D,并测得∠ACD=70°,∠BCD=45°.根据以上数据,请求出此时执法船距离小黄鱼岛D的距离CD的值.(参考数据:tan70°≈2.75,sin70°≈0.94,cos70°≈0.34,结果精确到1米.)
12.如图所示是自动卸货汽车卸货的状态图和其示意图,汽车的车厢采用液压机构,车厢的支撑顶杆AB的底部支撑点B在水平线OP的下方,OB与水平线OP夹角是15°,卸货时车厢与水平线OP成40°,此时OB与支持顶杆AB的夹角为45°,若OA=3米,求AB的长度.(精确到十分位,sin80°≈0.9848,cos80°≈0.1736,tan80°≈5.6712)
13.“新冠疫情”期间学校在校门口搭建如图1所示的遮阳棚,图2、图3是遮阳棚支架的示意图.遮阳棚支架由相同的菱形和相同的等腰三角形构成,滑块E,H可分别沿等长的立柱AB,DC上下移动,AF=EF=FG=1m,AB=2.4m.
(1)若移动滑块使∠AFE=90°,求棚宽BC的长(精确到0.01).
(2)在遮阳棚内安装如图4所示的红外线测温门(门高1.8m),门的顶端应与E点持平或低于E点,试问此时∠AFE最大为多少度?(结果精确到0.1m,参考数据:≈1.41,sin17.5°≈0.30,cos17.5°≈0.95,tan17.5°≈0.32)
14.2020年11月24日4时30分,我国在中国文昌航天发射场,用长征五号遥五运载火箭成功发射探月工程嫦娥五号探测器,火箭飞行约2200秒后,顺利将探测器送入预定轨道,开启我国首次地外天体采样返回之旅.如图,火箭从地面O处发射,当火箭达到A点时,从位于地面C处雷达站测得AC的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.求这枚火箭从A到B的平均速度是多少?(结果精确到0.01)(参考数据:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0905,sin45.5°≈0.71,cos45.5°0.70,tan45.5°≈1.02)
15.如图,大楼AB高10米,远处有一雕像(含底座).某人在楼顶A测得雕像顶C点的仰角为30°,此人从楼底B向雕像水平方向前进2米到达点E,在E处测得C点的仰角为53°.已知雕像底座DF的高是8米,求雕像CF的高.(参考数据:sin53°=,cos53°=,tan53°=,≈1.7,计算结果精确到1m.)
16.2020年6月23日,北斗卫星最后一颗全球组网卫星发射成功.运载火箭从地面A处(忽略发射塔高度)竖直向上发射,当运载火箭到达点B处时,地面D处的雷达站测得B处仰角为37°,BD=50km.10秒后,运载火箭直线上升到达点C处,此时地面E处一观测点测得C处的仰角为56°,已知点A,D,E在同一条直线上,并且D,E两处相距15km,求运载火箭从B处到C处时的平均速度(单位:km/s).
(参考数值:sin37°≈,cos37°≈,tan37°≈,sin56°≈,cos56°≈,tan56°≈)
17.2021年3月1日,我国第一部流域保护法﹣﹣《中华人民共和国长江保护法》正式实施.作为我国经济发展的重要引擎,长期以来,生态保护为发展让路一直是长江流域生态环境保护工作的痛点,长江保护法最大的特点就是“生态优先、绿色发展”的国家战略被写入法律.已知渔政执法船某一时刻在长江流域巡航时,从A出发以30千米/时的速度向正南方向行驶,在A处观测到码头C位于船的南偏东37°,2小时候到达B处,这时观察到码头C位于船的北偏东45°方向,若此时渔政执法船返回码头C,需要多少时间?(结果精确到0.1,≈1.41,sin37°≈,cos37°≈,tan37°≈).
18.如图,在一笔直的海岸线l上有相距2km的A、B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在东北方向上,则船C到海岸线L的距离是多少km?
19.随着我国首艘自主建造航母“山东舰”的正式服役,标志者我国已进入“双航母”时代.已知“山东舰”舰长BD为315m,航母前端点E到水平甲板BD的距离DE为6m,舰岛顶端A到BD的距离是AC,经测量,∠BAC=71.6°,∠EAC==80.6°.(参考数据:sin71.6°≈0.95,cos71.6°≈0.32,tan71.6°≈3.01,sin80.6°≈0.99,cos80.6°≈0.16,tan80.6°≈6.04)
(1)若设AC=xm,用含x的代数式表示BC与CD的长度.
(2)请计算舰岛AC的高度(结果精确到1m).
20.某校数学兴趣小组实地测量两岸互相平行的一段河道的宽度.在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向东走150米到达C点,测得点B在点C的北偏西60°方向,如图.
(1)求∠ABC的度数;
(2)求这段河道的宽度.
参考答案
1.解:如图,延长CE交AB于点M,
由题意得,∠ACM=45°,∠AEM=60°,DF=CE=8米,CD=EF=BM=1.6米,
设AM=x米.
在Rt△ACM中,∠ACM=45°,
∴AM=CM=x,
在Rt△AEM中,∠AEM=60°,
∵tan∠AEM=,即tan60°=,
∴EM=,
又∵CM﹣EM=CE,
∴x﹣=8,
解得x=(4+4)米,
即AM=(4+4)米,
∴AB=AM+BM=(4+5.6)米,
答:教学楼AB的高度为(4+5.6)米.
2.解:(1)方案1:在河岸MN上的取点B,C,测量得到∠OBM=75°,∠OCM=56°,BC=31.2m.
如图,设AB=xm,
在Rt△OAB中,AB=,
在Rt△OAC中,AC=,
∵AC﹣AB=BC,
∴,
∴x≈78,
∴河宽OA为78m.
(2)方案2:在河岸MN上的取点B,C,在B处立标杆,在过点C且垂直于MN的直线上,确定点E,使得E,B,O共线,CL测量得到AB=48m,BC=16m,EC=26m.
如图,
∵∠OAB=∠ECB=90°,∠ABO=∠EBC,
∴△ABO∽△CBE,
∴,
∴,
∴OA=78,
∴河宽OA为78m.
3.解:(1)如图,过C作CF⊥AB于F,过D作DH⊥AB于H,
则四边形CDHF是矩形,
∴CD=HF=4m,DH=CF=3m,
在Rt△ADH中,坡度i=1:1=DH:AH,
∴AH=DH=3m,
在Rt△BCF中,∠B=60°,CF=3m,
∵tanB=,
∴BF===(m),
∴AB=AH+HF+FB=7+1.7≈8.7m;
即坝底AB的长约为8.7m;
(2)此加固工程对古树没有影响,理由如下:
由题意得,DH:EH=1:,
∴EH=DH=3(m),
∴AE=EH﹣AH=(3﹣3)m,
∵(3)2=27,(3+2.5)2=30.25,
∴3﹣3<2.5,
∴此加固工程对古树没有影响.
4.解:过A点作AE⊥CD于E点,
由题意得,四边形ABDE为矩形,
∵∠DAE=26.6°,BD=30m,
∴AE=BD=30m,tan26.6°=,
∴DE=tan26.6° AE=0.50×30=15m,
∵∠CAE=45°,
∴∠ACE=45°,
∴AE=EC,
∴CE=30m,
∴CD=CE+ED=30+15=45(m),
∴建筑物CD的高度是45m.
5.解:(1)①过点C作CG∥DE,过点A作AH⊥CG于H,过点C作CF⊥DE于点F,
则点C到直线DE的距离为CF,
在Rt△CDF中,
∵sin∠CDE=,
∴CF=CD sin60°=70×=35(mm).
②由图可知,点A到直线DE的距离为:AH+CF.
∵∠DCB=70°,
∴∠ACD=180°﹣∠DCB=110°,
∵CG∥DE,
∴∠GCD=∠CDE=60°.
∴∠ACH=∠ACD﹣∠DCG=50°.
在Rt△ACH中,
∵sin∠ACH=,
∴AH=AC sin∠ACH=(115﹣35)×sin50°≈80×0.8=64(mm),
∴点A到直线DE的距离为AH+CF=35+64=123.5≈124(mm).
(2)如下图所示,虚线部分为旋转后的位置,B的对应点为B′,C的对应点为C′,
则B′C′=BC=35mm,DC′=DC=70mm.
在Rt△B′C′D中,
∵tan∠B′DC′===0.5,tan26.6°≈0.5,
∴∠B′DC′=26.6°.
∴CD旋转的角度为∠CDC′=∠CDE﹣∠B′DC′=60°﹣26.6°=33.4°.
故答案为:33.4°.
6.解:过点O作OE⊥AB于点E,则BE=OD=3m,
设AE=xm,则AB=(x+3)m,A′E=(x+6)m,
∵∠AOE=45°,
∴OE=AE=xm,
∵∠A′OE=60°,
∴tan60°==,
即=,
解得x=3+3,
∴AB=3+3+3=(6+3)m.
7.解:过点 PD作 DE⊥AC 交 AC于点 E,DF⊥AB交 AB于点 F,
∵i=1:3,CD=10,
设 DE=xm,则 CE=3xm,
在 Rt△CED 中,x2+(3x)2=102,
解得:x=或x=﹣(舍),
∴DE=m,则CE=3m,
∵∠BDF=∠DBF=45°,
∴BF=DF,
设 BF=DF=m 米,则 AB=()米,AC=(m﹣3)米,
在 Rt△CAB 中,,
解得:m≈29.9,
∴AB=29.9+≈33.1(米),
答:塑像的高度约为 33.1米.
8.解:(1)在Rt△ARL中,RL=AR cos43°≈4.38(km),
(2)在Rt△ARL中,AL=AR sin43°≈4.08(km),
在Rt△BRL中,BL=RL tan45.54°≈4.468(km),
∴AB=BL﹣AL=0.388≈0.39(km),
∴速度为0.39km/s,
答:雷达站到发射处的水平距离为4.38km,这枚火箭从A到B的平均速度为0.39km/s.
9.解:在Rt△BCE中,BE=21,∠EBC=45°,
∴CE=BE=21米,
在Rt△ADE中,AE=BE+AB=21+6=27米,
∵∠EAD=30°,
∴DE=AE tan30°=9米,
∴CD=CE﹣DE=21﹣9(米).
答:该屏幕的高度CD为(21﹣9)米.
10.解:设AD=xm,
∵∠ABD=45°,
∴BD=AD=xm,
∵∠ACD=31°,BC=60m,
∴tan31°===0.60,
解得x=90.0,
∴他家到公路l的距离AD的长度约90.0m.
11.解:设CD=x米,
Rt△ACD中,tan∠ACD=,
∴AD=2.75x米,
Rt△BCD中,∠BCD=45°,
∴BD=CD=x米,
∴2.75x+x=3641,
解得x≈971,
答:执法船距离小黄鱼岛D的距离CD约为971米.
12.解:由题意得,∠ABO=45°,∠AOP=40°,∠BOP=15°,OA=3米,
过点O作OM⊥AB于M,
在△AOB中,由内角和定理可得,
∠A=180°﹣∠ABO﹣∠AOB
=180°﹣45°﹣40°﹣15°
=80°,
在Rt△AOM中,∠A=80°,OA=3米,
∴OM=OA sin80°≈3×0.9848≈2.95(米),
∴AM=OA cos80°≈3×0.1736≈0.52(米),
在Rt△BOM中,∠ABO=845°,
∴BM=OM=2.95米,
∴AB=AM+BM=2.95+0.52≈3.5(米),
答:AB的长度约为3.5米.
13.解:(1)过点F作FM⊥AB于M,
∵AF=EF=1m,∠AFE=90°,
∴∠MEF=45°,
∴MF=1×sin45°=m,
∴BC=×2+×3=4≈5.46m,
答:棚宽BC的长约为5.46m;
(2)当BE=1.8m时,AE=2.4﹣1.8=0.6m,如图,
∴ME==0.3m,EF=1m,
∴sin∠MFE==0.3,
∴∠MFE=17.5°,∠AFE=2∠MFE=35°,
答:∠AFE最大为35度.
14.解:在Rt△ACO中,AC=6km,∠ACO=42.4°,
∵cos∠ACO=,
∴OC=AC cos∠ACO=6×cos42.4°≈4.44(km),
在Rt△BCO中,OC=4.44km,∠BCO=45.5°,
∵tan∠BCO=,
∴BO=OC tan∠BCO=4.44×tan45.5°≈4.44×1.02=4.5288(km),
∵sin∠ACO=,
∴AO=ACsin∠ACO=6×sin42.4°≈4.02(km),
∴AB=BO﹣AO=4.5288﹣4.02=0.5088≈0.51(km).
∵时间为1秒,
∴这枚火箭从A到B的平均速度大约是0.51km/s,
答:这枚火箭从A到B的平均速度大约是0.51km/s.
15.解:如图,过点A作AG⊥CD于G,设CD=x,
∴四边形ABDG是矩形,
∴AG=BD,GD=AB,
∵∠CED=53°,
∴DE=,
∴AG=BD=+2,
∵∠CAG=30°,
∴CG=AG tan30°,即CD﹣GD=AG tan30°,
∴,
解得:x≈20,
∴CF=CD﹣DF=20﹣8=12(米),
答:雕像CF的高为12米.
16.解:由题意得,BD=50km,∠ADB=37°,DE=15km,∠AEC=56°,
在Rt△ABD中,
∵BD=50km,∠ADB=37°,
∴AB=sin37°×BD≈×50=30(km),AD=cos37°×BD≈×50=40(km),
∴AE=AD﹣DE=40﹣15=25(km),
在Rt△AEC中,∠AEC=56°,
∴AC=tan56°×AE≈×25=37(km),
∴BC=AC﹣AB=37﹣20≈17(km),
∴火箭的速度为17÷10≈1.7(km/s),
答:运载火箭从B处到C处时的平均速度约为1.7km/s.
17.解:过C作CD⊥AB于D,
由题意得,AB=30×2=60(千米/时),∠A=37°,∠B=45°,
设CD=BD=x,
在Rt△BCD中,∵∠B=45°,∠BDC=90°,
∴CD=BD=x,
在Rt△ACD中,∵∠A=37°,∠ADC=90°,
∴AD=≈=,
∵AD+BD=AB,
∴x+x=60,
解得:x≈25.7,
∴BC=BD=25.7×≈37.1(千米),
∵37.1÷30≈1.2(小时),
答:渔政执法船返回码头C,需要1.2小时.
18.解:过点C作CD⊥AB于点D,如图所示:
则∠CDA=90°,
设CD=xkm,
根据题意得:∠CAD=90°﹣60°=30°,∠CBD=90°﹣45°=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=xkm,
在Rt△ACD中,∠CAD=30°,
∴AC=2CD=2x(km),
∴AD=CD=x(km),
∵AD﹣BD=AB,
∴x﹣x=2,
解得:x=+1,
即CD=(+1)km,
答:船C到海岸线l的距离是(+1)km.
19.解:(1)作EH⊥AC于H,
则四边形EHCD是矩形,
在Rt△ABC中,
∵tan∠BAC=,
∴BC=AC tan71.6°=3.01xm,
在Rt△AHE中,
∵tan∠EAC=,
∴CD=EH=AH tan80.6°=6.04(x﹣6)=(6.04x﹣36.24)m;
(2)设AC=xm,
∵四边形EHCD是矩形,
∴DE=CH=6m,
∵BD=BC+CD=315m,BC=3.01xm,CD=(6.04x﹣36.24)m,
∴3.01x+6.04x﹣36.24=315,
解得:x=39,
∴舰岛AC的高度为:39m.
20.解:(1)由题意得,∠BAC=45°,∠BCA=30°,
∴∠ABC=180°﹣∠BAD﹣∠BCA=105°;
(2)如图,作BD⊥CA交CA的延长线于D,
设BD=x米,
∵∠BCA=30°,
∴CD=x(米),
∵∠BAD=45°,
∴AD=BD=x米,
∴x+x=150,
解得x=75(﹣1)≈54.8,
答:这段河的宽约为54.8米.
1.某校数学兴趣小组学完“三角函数的应用”后,在校园内利用三角尺测量教学楼AB的高度,如图,小明同学站在点D处,将含45°角三角尺的一条直角边水平放置,此时三角尺的倾斜边刚好落在视线CA上,沿教学楼向前走8米到达点F处,将含30°角三角尺的短直角边水平放置,此时三角尺的斜边也刚好落在视线EA上,已知小明眼睛到地面的距离为1.6米,求教学楼AB的高度.(点D,F,B在同一水平线上,结果保留根号)
2.如图,小明在笔直的河岸MN上的点A处,以正对岸明显的标志点O为参照点,设计出测量河宽OA的方案,绘制了相应的示意图,并用测角仪、卷尺及标杆测得一些数据如下:
(1)请你结合示意图,简述选择标志点O为参照点之后的测量过程;
(2)按照方案,求河宽OA.(参考数据:tan75°≈,tan56°≈)
3.水坝的横截面是梯形ABCD,现测得坝顶DC=4m,坡面AD的坡度i为1:1,坡面BC的坡角β为60°,坝高3m,(≈1.732)求:
(1)坝底AB的长(精确到0.1);
(2)水利部门为了加固水坝,在保持坝顶CD不变的情况下降低AD的坡度(如图),使新坡面DE的坡度i为1:,原水坝底部正前方2.5m处有一千年古树,此加固工程对古树是否有影响?请说明理由.
4.如图,平地上两栋建筑物AB和CD相距30m,在建筑物AB的顶部测得建筑物CD底部的俯角为26.6°,测得建筑物CD顶部的仰角为45°.求建筑物CD的高度.(参考数据:sin16.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50)
5.图①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图,托板长AB=115mm,支撑板长CD=70mm,板AB固定在支撑板顶点C处,且CB=35mm,托板AB可绕点C转动,支撑板CD可绕点D转动.
(1)当∠CDE=60°时,
①求点C到直线DE的距离(计算结果保留根号);
②若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);
(2)为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在直线DE上即可,则CD旋转的角度为 .(直接写出结果)
(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,≈1.7)
6.小宸想利用测量知识测算湖中小山的高度.他站在湖边看台上,清晰地看到小山倒映在平静的湖水中,如图所示,他在点O处测得小山顶端的仰角为45°,小山顶端A在水中倒影A′的俯角为60°.已知:点O到湖面的距离OD=3m,OD⊥DB,AB⊥DB,A、B、A′三点共线,A'B=AB,求小山的高度AB.(光线的折射忽略不计;结果保留根号)
7.大汉雄风坐落于河南省永城市芒砀山主峰,是为纪念刘邦在芒砀山斩蛇起义创建四百年大汉王朝而建,某数学兴趣小组想测量底座之上部分雕像AB的高度,如图在和雕塑底座上端水平的山坡C处测得雕塑顶端B的仰角为58.5°,沿山坡上行10米到达点D,测得雕塑顶端B的仰角为45°,已知山坡的坡度i=1:3,且A,C在同一水平地面上,求塑像AB的高度.(测倾器高度忽略不计,结果精确到0.1米,参考数据:sin58.5°≈0.85,cos58.5°≈0.52,tan58.5°≈1.63,≈1.4,≈1.7,≈3.2.)
8.北京时间2020年11月24日04时30分,在海南文昌发射中心,嫦娥五号搭载长征五号遥五运载火箭发射升空,为我国探月工程中“绕、落、回”三步战略画上完美句号.如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站测得AR的距离是6km,仰角为43°;1s后火箭到达B点,此时测得仰角为45.54°(所有结果取小数点后两位).
(1)求地面雷达站R到发射处L的水平距离;
(2)求这枚火箭从A到B的平均速度是多少?
(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93,sin45.54°≈0.71,cos45.54°≈0.70,tan45.54°≈1.02)
9.如图,甲乙两名同学在万达广场上观测商场墙上的大屏幕CD,点A是甲同学的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6米到达B处,又测得该屏幕上端C处的仰角为45°,继续向前行走到墙壁的下端,乙同学负责测量,测得BE=21米,请你计算出该屏幕的高度CD.(结果保留根号)
10.如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l,小明测量出∠ACD=31°,∠ABD=45°,BC=60m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
11.钓鱼岛是我国固有领土,2021年4月26日,中华人民共和国自然资源部在其官网上公布《钓鱼岛及其附属岛屿地形地貌调查报告》,报告公布了钓鱼岛及其附属岛屿的高分辨率海岛地形数据.如图所示,点A是岛上最西端“西钓角”,点B是岛上最东端“东钓角”,AB长约3641米,点D是岛上的小黄鱼岛,且A、B、D三点共线.某日中国海监一艘执法船巡航到点C处时,恰好看到正北方的小黄鱼岛D,并测得∠ACD=70°,∠BCD=45°.根据以上数据,请求出此时执法船距离小黄鱼岛D的距离CD的值.(参考数据:tan70°≈2.75,sin70°≈0.94,cos70°≈0.34,结果精确到1米.)
12.如图所示是自动卸货汽车卸货的状态图和其示意图,汽车的车厢采用液压机构,车厢的支撑顶杆AB的底部支撑点B在水平线OP的下方,OB与水平线OP夹角是15°,卸货时车厢与水平线OP成40°,此时OB与支持顶杆AB的夹角为45°,若OA=3米,求AB的长度.(精确到十分位,sin80°≈0.9848,cos80°≈0.1736,tan80°≈5.6712)
13.“新冠疫情”期间学校在校门口搭建如图1所示的遮阳棚,图2、图3是遮阳棚支架的示意图.遮阳棚支架由相同的菱形和相同的等腰三角形构成,滑块E,H可分别沿等长的立柱AB,DC上下移动,AF=EF=FG=1m,AB=2.4m.
(1)若移动滑块使∠AFE=90°,求棚宽BC的长(精确到0.01).
(2)在遮阳棚内安装如图4所示的红外线测温门(门高1.8m),门的顶端应与E点持平或低于E点,试问此时∠AFE最大为多少度?(结果精确到0.1m,参考数据:≈1.41,sin17.5°≈0.30,cos17.5°≈0.95,tan17.5°≈0.32)
14.2020年11月24日4时30分,我国在中国文昌航天发射场,用长征五号遥五运载火箭成功发射探月工程嫦娥五号探测器,火箭飞行约2200秒后,顺利将探测器送入预定轨道,开启我国首次地外天体采样返回之旅.如图,火箭从地面O处发射,当火箭达到A点时,从位于地面C处雷达站测得AC的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.求这枚火箭从A到B的平均速度是多少?(结果精确到0.01)(参考数据:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0905,sin45.5°≈0.71,cos45.5°0.70,tan45.5°≈1.02)
15.如图,大楼AB高10米,远处有一雕像(含底座).某人在楼顶A测得雕像顶C点的仰角为30°,此人从楼底B向雕像水平方向前进2米到达点E,在E处测得C点的仰角为53°.已知雕像底座DF的高是8米,求雕像CF的高.(参考数据:sin53°=,cos53°=,tan53°=,≈1.7,计算结果精确到1m.)
16.2020年6月23日,北斗卫星最后一颗全球组网卫星发射成功.运载火箭从地面A处(忽略发射塔高度)竖直向上发射,当运载火箭到达点B处时,地面D处的雷达站测得B处仰角为37°,BD=50km.10秒后,运载火箭直线上升到达点C处,此时地面E处一观测点测得C处的仰角为56°,已知点A,D,E在同一条直线上,并且D,E两处相距15km,求运载火箭从B处到C处时的平均速度(单位:km/s).
(参考数值:sin37°≈,cos37°≈,tan37°≈,sin56°≈,cos56°≈,tan56°≈)
17.2021年3月1日,我国第一部流域保护法﹣﹣《中华人民共和国长江保护法》正式实施.作为我国经济发展的重要引擎,长期以来,生态保护为发展让路一直是长江流域生态环境保护工作的痛点,长江保护法最大的特点就是“生态优先、绿色发展”的国家战略被写入法律.已知渔政执法船某一时刻在长江流域巡航时,从A出发以30千米/时的速度向正南方向行驶,在A处观测到码头C位于船的南偏东37°,2小时候到达B处,这时观察到码头C位于船的北偏东45°方向,若此时渔政执法船返回码头C,需要多少时间?(结果精确到0.1,≈1.41,sin37°≈,cos37°≈,tan37°≈).
18.如图,在一笔直的海岸线l上有相距2km的A、B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在东北方向上,则船C到海岸线L的距离是多少km?
19.随着我国首艘自主建造航母“山东舰”的正式服役,标志者我国已进入“双航母”时代.已知“山东舰”舰长BD为315m,航母前端点E到水平甲板BD的距离DE为6m,舰岛顶端A到BD的距离是AC,经测量,∠BAC=71.6°,∠EAC==80.6°.(参考数据:sin71.6°≈0.95,cos71.6°≈0.32,tan71.6°≈3.01,sin80.6°≈0.99,cos80.6°≈0.16,tan80.6°≈6.04)
(1)若设AC=xm,用含x的代数式表示BC与CD的长度.
(2)请计算舰岛AC的高度(结果精确到1m).
20.某校数学兴趣小组实地测量两岸互相平行的一段河道的宽度.在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向东走150米到达C点,测得点B在点C的北偏西60°方向,如图.
(1)求∠ABC的度数;
(2)求这段河道的宽度.
参考答案
1.解:如图,延长CE交AB于点M,
由题意得,∠ACM=45°,∠AEM=60°,DF=CE=8米,CD=EF=BM=1.6米,
设AM=x米.
在Rt△ACM中,∠ACM=45°,
∴AM=CM=x,
在Rt△AEM中,∠AEM=60°,
∵tan∠AEM=,即tan60°=,
∴EM=,
又∵CM﹣EM=CE,
∴x﹣=8,
解得x=(4+4)米,
即AM=(4+4)米,
∴AB=AM+BM=(4+5.6)米,
答:教学楼AB的高度为(4+5.6)米.
2.解:(1)方案1:在河岸MN上的取点B,C,测量得到∠OBM=75°,∠OCM=56°,BC=31.2m.
如图,设AB=xm,
在Rt△OAB中,AB=,
在Rt△OAC中,AC=,
∵AC﹣AB=BC,
∴,
∴x≈78,
∴河宽OA为78m.
(2)方案2:在河岸MN上的取点B,C,在B处立标杆,在过点C且垂直于MN的直线上,确定点E,使得E,B,O共线,CL测量得到AB=48m,BC=16m,EC=26m.
如图,
∵∠OAB=∠ECB=90°,∠ABO=∠EBC,
∴△ABO∽△CBE,
∴,
∴,
∴OA=78,
∴河宽OA为78m.
3.解:(1)如图,过C作CF⊥AB于F,过D作DH⊥AB于H,
则四边形CDHF是矩形,
∴CD=HF=4m,DH=CF=3m,
在Rt△ADH中,坡度i=1:1=DH:AH,
∴AH=DH=3m,
在Rt△BCF中,∠B=60°,CF=3m,
∵tanB=,
∴BF===(m),
∴AB=AH+HF+FB=7+1.7≈8.7m;
即坝底AB的长约为8.7m;
(2)此加固工程对古树没有影响,理由如下:
由题意得,DH:EH=1:,
∴EH=DH=3(m),
∴AE=EH﹣AH=(3﹣3)m,
∵(3)2=27,(3+2.5)2=30.25,
∴3﹣3<2.5,
∴此加固工程对古树没有影响.
4.解:过A点作AE⊥CD于E点,
由题意得,四边形ABDE为矩形,
∵∠DAE=26.6°,BD=30m,
∴AE=BD=30m,tan26.6°=,
∴DE=tan26.6° AE=0.50×30=15m,
∵∠CAE=45°,
∴∠ACE=45°,
∴AE=EC,
∴CE=30m,
∴CD=CE+ED=30+15=45(m),
∴建筑物CD的高度是45m.
5.解:(1)①过点C作CG∥DE,过点A作AH⊥CG于H,过点C作CF⊥DE于点F,
则点C到直线DE的距离为CF,
在Rt△CDF中,
∵sin∠CDE=,
∴CF=CD sin60°=70×=35(mm).
②由图可知,点A到直线DE的距离为:AH+CF.
∵∠DCB=70°,
∴∠ACD=180°﹣∠DCB=110°,
∵CG∥DE,
∴∠GCD=∠CDE=60°.
∴∠ACH=∠ACD﹣∠DCG=50°.
在Rt△ACH中,
∵sin∠ACH=,
∴AH=AC sin∠ACH=(115﹣35)×sin50°≈80×0.8=64(mm),
∴点A到直线DE的距离为AH+CF=35+64=123.5≈124(mm).
(2)如下图所示,虚线部分为旋转后的位置,B的对应点为B′,C的对应点为C′,
则B′C′=BC=35mm,DC′=DC=70mm.
在Rt△B′C′D中,
∵tan∠B′DC′===0.5,tan26.6°≈0.5,
∴∠B′DC′=26.6°.
∴CD旋转的角度为∠CDC′=∠CDE﹣∠B′DC′=60°﹣26.6°=33.4°.
故答案为:33.4°.
6.解:过点O作OE⊥AB于点E,则BE=OD=3m,
设AE=xm,则AB=(x+3)m,A′E=(x+6)m,
∵∠AOE=45°,
∴OE=AE=xm,
∵∠A′OE=60°,
∴tan60°==,
即=,
解得x=3+3,
∴AB=3+3+3=(6+3)m.
7.解:过点 PD作 DE⊥AC 交 AC于点 E,DF⊥AB交 AB于点 F,
∵i=1:3,CD=10,
设 DE=xm,则 CE=3xm,
在 Rt△CED 中,x2+(3x)2=102,
解得:x=或x=﹣(舍),
∴DE=m,则CE=3m,
∵∠BDF=∠DBF=45°,
∴BF=DF,
设 BF=DF=m 米,则 AB=()米,AC=(m﹣3)米,
在 Rt△CAB 中,,
解得:m≈29.9,
∴AB=29.9+≈33.1(米),
答:塑像的高度约为 33.1米.
8.解:(1)在Rt△ARL中,RL=AR cos43°≈4.38(km),
(2)在Rt△ARL中,AL=AR sin43°≈4.08(km),
在Rt△BRL中,BL=RL tan45.54°≈4.468(km),
∴AB=BL﹣AL=0.388≈0.39(km),
∴速度为0.39km/s,
答:雷达站到发射处的水平距离为4.38km,这枚火箭从A到B的平均速度为0.39km/s.
9.解:在Rt△BCE中,BE=21,∠EBC=45°,
∴CE=BE=21米,
在Rt△ADE中,AE=BE+AB=21+6=27米,
∵∠EAD=30°,
∴DE=AE tan30°=9米,
∴CD=CE﹣DE=21﹣9(米).
答:该屏幕的高度CD为(21﹣9)米.
10.解:设AD=xm,
∵∠ABD=45°,
∴BD=AD=xm,
∵∠ACD=31°,BC=60m,
∴tan31°===0.60,
解得x=90.0,
∴他家到公路l的距离AD的长度约90.0m.
11.解:设CD=x米,
Rt△ACD中,tan∠ACD=,
∴AD=2.75x米,
Rt△BCD中,∠BCD=45°,
∴BD=CD=x米,
∴2.75x+x=3641,
解得x≈971,
答:执法船距离小黄鱼岛D的距离CD约为971米.
12.解:由题意得,∠ABO=45°,∠AOP=40°,∠BOP=15°,OA=3米,
过点O作OM⊥AB于M,
在△AOB中,由内角和定理可得,
∠A=180°﹣∠ABO﹣∠AOB
=180°﹣45°﹣40°﹣15°
=80°,
在Rt△AOM中,∠A=80°,OA=3米,
∴OM=OA sin80°≈3×0.9848≈2.95(米),
∴AM=OA cos80°≈3×0.1736≈0.52(米),
在Rt△BOM中,∠ABO=845°,
∴BM=OM=2.95米,
∴AB=AM+BM=2.95+0.52≈3.5(米),
答:AB的长度约为3.5米.
13.解:(1)过点F作FM⊥AB于M,
∵AF=EF=1m,∠AFE=90°,
∴∠MEF=45°,
∴MF=1×sin45°=m,
∴BC=×2+×3=4≈5.46m,
答:棚宽BC的长约为5.46m;
(2)当BE=1.8m时,AE=2.4﹣1.8=0.6m,如图,
∴ME==0.3m,EF=1m,
∴sin∠MFE==0.3,
∴∠MFE=17.5°,∠AFE=2∠MFE=35°,
答:∠AFE最大为35度.
14.解:在Rt△ACO中,AC=6km,∠ACO=42.4°,
∵cos∠ACO=,
∴OC=AC cos∠ACO=6×cos42.4°≈4.44(km),
在Rt△BCO中,OC=4.44km,∠BCO=45.5°,
∵tan∠BCO=,
∴BO=OC tan∠BCO=4.44×tan45.5°≈4.44×1.02=4.5288(km),
∵sin∠ACO=,
∴AO=ACsin∠ACO=6×sin42.4°≈4.02(km),
∴AB=BO﹣AO=4.5288﹣4.02=0.5088≈0.51(km).
∵时间为1秒,
∴这枚火箭从A到B的平均速度大约是0.51km/s,
答:这枚火箭从A到B的平均速度大约是0.51km/s.
15.解:如图,过点A作AG⊥CD于G,设CD=x,
∴四边形ABDG是矩形,
∴AG=BD,GD=AB,
∵∠CED=53°,
∴DE=,
∴AG=BD=+2,
∵∠CAG=30°,
∴CG=AG tan30°,即CD﹣GD=AG tan30°,
∴,
解得:x≈20,
∴CF=CD﹣DF=20﹣8=12(米),
答:雕像CF的高为12米.
16.解:由题意得,BD=50km,∠ADB=37°,DE=15km,∠AEC=56°,
在Rt△ABD中,
∵BD=50km,∠ADB=37°,
∴AB=sin37°×BD≈×50=30(km),AD=cos37°×BD≈×50=40(km),
∴AE=AD﹣DE=40﹣15=25(km),
在Rt△AEC中,∠AEC=56°,
∴AC=tan56°×AE≈×25=37(km),
∴BC=AC﹣AB=37﹣20≈17(km),
∴火箭的速度为17÷10≈1.7(km/s),
答:运载火箭从B处到C处时的平均速度约为1.7km/s.
17.解:过C作CD⊥AB于D,
由题意得,AB=30×2=60(千米/时),∠A=37°,∠B=45°,
设CD=BD=x,
在Rt△BCD中,∵∠B=45°,∠BDC=90°,
∴CD=BD=x,
在Rt△ACD中,∵∠A=37°,∠ADC=90°,
∴AD=≈=,
∵AD+BD=AB,
∴x+x=60,
解得:x≈25.7,
∴BC=BD=25.7×≈37.1(千米),
∵37.1÷30≈1.2(小时),
答:渔政执法船返回码头C,需要1.2小时.
18.解:过点C作CD⊥AB于点D,如图所示:
则∠CDA=90°,
设CD=xkm,
根据题意得:∠CAD=90°﹣60°=30°,∠CBD=90°﹣45°=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=xkm,
在Rt△ACD中,∠CAD=30°,
∴AC=2CD=2x(km),
∴AD=CD=x(km),
∵AD﹣BD=AB,
∴x﹣x=2,
解得:x=+1,
即CD=(+1)km,
答:船C到海岸线l的距离是(+1)km.
19.解:(1)作EH⊥AC于H,
则四边形EHCD是矩形,
在Rt△ABC中,
∵tan∠BAC=,
∴BC=AC tan71.6°=3.01xm,
在Rt△AHE中,
∵tan∠EAC=,
∴CD=EH=AH tan80.6°=6.04(x﹣6)=(6.04x﹣36.24)m;
(2)设AC=xm,
∵四边形EHCD是矩形,
∴DE=CH=6m,
∵BD=BC+CD=315m,BC=3.01xm,CD=(6.04x﹣36.24)m,
∴3.01x+6.04x﹣36.24=315,
解得:x=39,
∴舰岛AC的高度为:39m.
20.解:(1)由题意得,∠BAC=45°,∠BCA=30°,
∴∠ABC=180°﹣∠BAD﹣∠BCA=105°;
(2)如图,作BD⊥CA交CA的延长线于D,
设BD=x米,
∵∠BCA=30°,
∴CD=x(米),
∵∠BAD=45°,
∴AD=BD=x米,
∴x+x=150,
解得x=75(﹣1)≈54.8,
答:这段河的宽约为54.8米.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
