24.1.2 垂直于直径的弦 同步练习题(含解析)
文档属性
| 名称 | 24.1.2 垂直于直径的弦 同步练习题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-13 20:48:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2021年九年级上册:24.1.2 垂直于直径的弦 同步练习题
一、选择题
1.上体育课时,老师在运动场上教同学们学习掷铅球,训练时,李力同学掷出的铅球在场地上砸出了一个坑口直径约为10cm,深约为2cm的小坑,则该铅球的直径约为( )
A.20cm B.19.5cm C.14.5cm D.10cm
2.“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是( )
A.12寸 B.24寸 C.13寸 D.26寸
3.如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( )
A.50m B.45m C.40m D.60m
4.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽,则水的最大深度为( )
A.8cm B.10cm C.14cm D.16cm
5.如图,在半径为的⊙O中,弦AB,CD互相垂直,垂足为点P.若AB=CD=8,则OP的长为( )
A. B.
C.4 D.2
6.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )
A.10cm B.10cm C.10cm D.8cm
7.如图,OA为⊙O的半径,弦BC⊥OA于点P.若BC=8,AP=2,则⊙O的半径长为( )
A.5 B.6 C.10 D.
8.如图,在⊙O中,半径r=5,弦AB=8,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
A.2个 B.5个 C.4个 D.3个
二、填空题
9.如图,的直径为,弦长为,点在上运动,则的最小值是____.
10.已知:如图,AB是⊙O的弦,半径OC交弦AB于点P,且AB=10cm,PB=4cm,PC=2cm,则圆心O 到AB的距离为______cm.
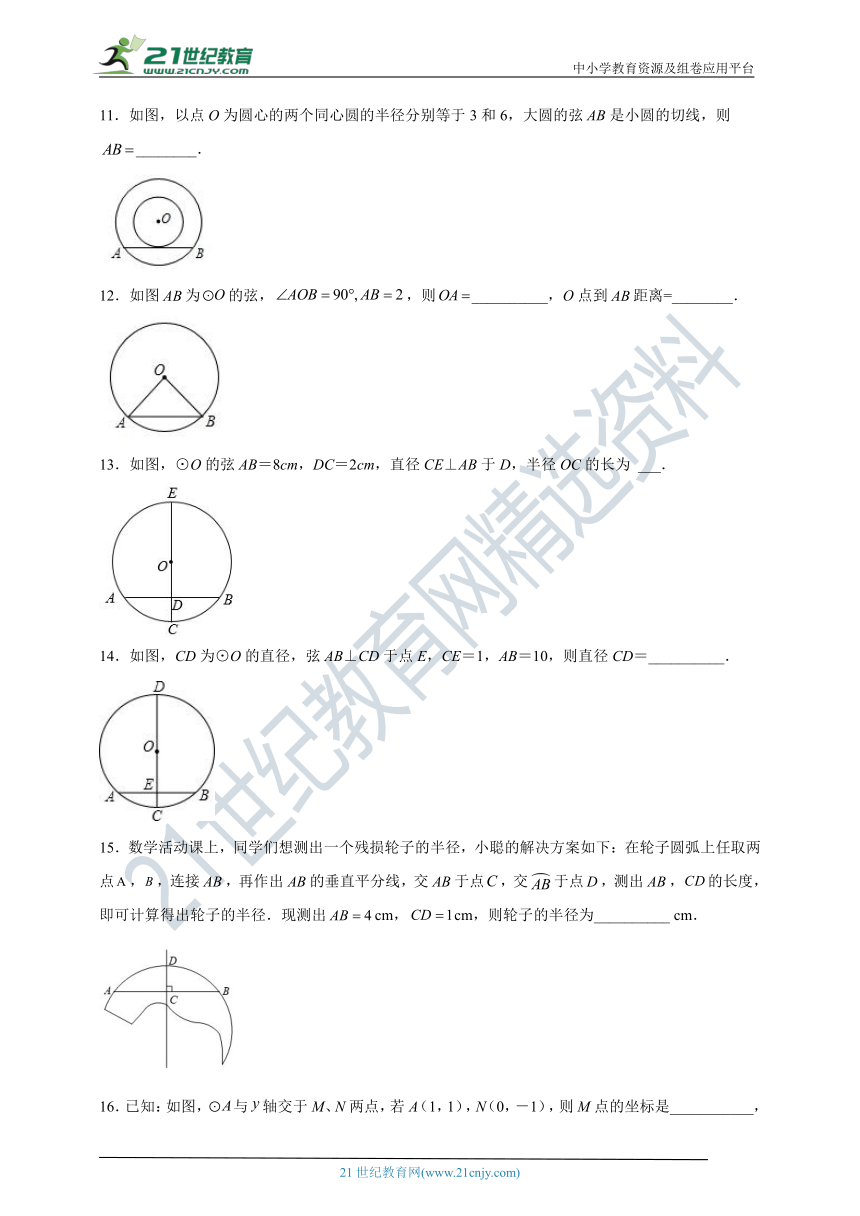
11.如图,以点O为圆心的两个同心圆的半径分别等于3和6,大圆的弦AB是小圆的切线,则________.
12.如图为的弦,,则__________,O点到距离=________.
13.如图,⊙O的弦AB=8cm,DC=2cm,直径CE⊥AB于D,半径OC的长为 ___.
14.如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,则直径CD=__________.
15.数学活动课上,同学们想测出一个残损轮子的半径,小聪的解决方案如下:在轮子圆弧上任取两点,,连接,再作出的垂直平分线,交于点,交于点,测出,的长度,即可计算得出轮子的半径.现测出cm,cm,则轮子的半径为__________ cm.
16.已知:如图,与轴交于M、N两点,若A(1,1),N(0,-1),则M点的坐标是___________,的半径是_______.
三、解答题
17.一个残破的车轮如图所示,测得它所剩圆弧两端点间的距离,弧的中点到弧所对弦的距离,如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少?(结果精确到)
18.如图,工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10cm,测得钢珠顶端离零件表面的距离为8cm,则这个小圆孔的宽口AB的长度为多少?
19.如图,CD为的直径,弦于E,如果,,求半径OC的长
20.1400多年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的跨度(即弧所对的弦长)为,拱高(即弧的中点到弦的距离)为,求桥拱所在圆的半径(结果精确到).
21.如图,为⊙的直径,弦与交于点,,.
(1)求的度数;
(2)若,求的长.
22.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,
(1)求⊙O的半径;
(2)求O到弦BC的距离.
参考答案
1.C
【分析】
根据垂径定理,构造直角三角形,小坑的直径就是圆中的弦长,小坑的深就是拱高,利用勾股定理,设出未知数,列出方程,即可求出铅球的直径.
【详解】
解:根据题意,画出图形如图所示,
由题意知,,,是半径,且,
,
设铅球的半径为,则,
在中,根据勾股定理,,
即,
解得:,
所以铅球的直径为:cm,
故选:C.
【点睛】
本题考查的是垂径定理和勾股定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为,弦长为,这条弦的弦心距为,则成立,知道这三个量中的任意两个,就可以求出另外一个.
2.D
【分析】
根据垂径定理和勾股定理求解.
【详解】
解:连接OA,如图所示,
设直径CD的长为2x,则半径OC=x,
∵CD为⊙O的直径,弦AB⊥CD于E,AB=10寸,
∴AE=BE=AB=×10=5寸,
∵OA为⊙O的半径,,则OA=x寸,
根据勾股定理得x2=52+(x-1)2,
解得x=13,
CD=2x=2×13=26(寸).
故选:D.
【点睛】
本题考查了垂径定理和勾股定理.正确的作出辅助线是解题的关键.
3.A
【分析】
设圆弧的圆心为O,过O作OC⊥AB于C,交于D,连接OA,先由垂径定理得AC=BC=AB=150,再由勾股定理求出OC=200,然后求出CD的长即可.
【详解】
解:设圆弧的圆心为O,过O作OC⊥AB于C,交于D,连接OA,如图所示:
则OA=OD=250,AC=BC=AB=150,
∴OC===200(m),
∴CD=OD﹣OC=250﹣200=50(m),
即这些钢索中最长的一根为50m,
故选:A.
【点睛】
本题考查了垂径定理和勾股定理等知识;熟练掌握垂径定理和勾股定理是解题的关键.
4.D
【分析】
连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD的长,进而可得出CD的长.
【详解】
解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,(cm),
∴CD=OC-OD=26-10=16(cm),
故选:D.
【点睛】
本题考查了垂径定理、勾股定理等知识;根据题意作出辅助线,构造出直角三角形是解答此题的关键.
5.B
【分析】
作OM⊥AB于M,ON⊥CD于N,连接OA,OC,根据垂径定理得出BM=AM=4,DN=CN=4,根据勾股定理求出OM和ON,证明四边形OMPN是正方形,即可解决问题.
【详解】
解:如图,作OM⊥AB于M,ON⊥CD于N,连接OA,OC.
∴AM=BM=4,CN=DN=4,
∵OA=OC=2,
∴OM=,
ON=,
∴OM=ON,
∵AB⊥CD,
∴∠OMP=∠ONP=∠MPN=90°,
∴四边形OMPN是矩形,
∵OM=ON,
∴四边形OMPN是正方形,
∴OP=OM=2,
故选:B.
【点睛】
本题考查了垂径定理,勾股定理,正方形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考常考题型.
6.B
【分析】
首先找到EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,设OF=x,则OM是16-x,MF=8,然后在直角三角形MOF中利用勾股定理求得OF的长即可.
【详解】
解:取EF的中点M,作MN⊥AD于点M,
根据垂径定理知球心O在MN上,连接OF,
设OF=x,则OM=16-x,MF=8,
在直角三角形OMF中,OM2+MF2=OF2,
即:(16-x)2+82=x2,
解得:x=10.
即球的半径为10cm.
故选:B.
【点睛】
本题主考查垂径定理及勾股定理的知识,正确作出辅助线构造直角三角形是解题的关键.
7.A
【分析】
连接OB,根据垂径定理和勾股定理列方程即可.
【详解】
解:如图所示,连接OB,
∵,,
∴,,
∵,
∴,
解得,,
则的半径长为,
故选A.
【点睛】
本题考查了垂径定理和勾股定理,解题关键是连接半径,构建直角三角形,列方程解决问题.
8.D
【分析】
当P为AB的中点时OP最短,利用垂径定理得到OP垂直于AB,在直角三角形AOP中,由OA与AP的长,利用勾股定理求出OP的长;当P与A或B重合时,OP最长,求出OP的范围,由OP为整数,即可得到OP所有可能的长.
【详解】
解:当P为AB的中点时,利用垂径定理得到OP⊥AB,此时OP最短,
∵AB=8,∴AP=BP=4,
在直角三角形AOP中,OA=5,AP=4,
根据勾股定理得:OP==,即OP的最小值为3;
当P与A或B重合时,OP最长,此时OP=5,
∴3≤OP<5,
则使线段OP的长度为整数,
∴OP=3,4
根据对称性可知,满足条件的点P的个数有3个
故选:D.
【点睛】
此题考查了垂径定理,以及勾股定理,熟练掌握垂径定理,以及勾股定理是解本题的关键.
9.3
【分析】
根据“点到直线的最短距离是垂线段的长度”知当OP⊥AB时,OP的值最小.连接OA,在直角三角形OAP中由勾股定理即可求得OP的长度.
【详解】
解:当OP⊥AB时,OP的值最小,
则AP′=BP′=AB=4,
如图所示,连接OA,
在Rt△OAP′中,AP′=4,OA=5,
则根据勾股定理知OP′=3,即OP的最小值为3.
【点睛】
本题考查了勾股定理、垂径定理.掌握垂线段最短是解题的关键.
10.
【分析】
过点作于,连接,由垂径定理得,则,设,在和中,由勾股定理得,解得即可,再在中利用勾股定理求出.
【详解】
解:过点作于,连接,如图所示:
则,
,
设,
在和中,
由勾股定理得:,
即,
解得:,
即半径的长为7,
在中,
,
则圆心O到AB的距离为,
故答案是:.
【点睛】
本题考查了垂径定理、勾股定理,解题的关键是熟练掌握垂径定理,由勾股定理得出方程,再求解.
11.
【分析】
连结OP、OA,如图,根据切线的性质得OP⊥AB,再根据垂径定理得到AP=BP,然后在Rt△AOP中,利用勾股定理可计算出AP=,再利用AB=2AP进行计算即可.
【详解】
解:连接OP、OA,如图,
∵大圆的弦AB是小圆的切线,点P为切点,
∴OP⊥AB,
∴AP=BP,
在Rt△AOP中,∵OP=3,OA=6,
∴AP=,
∴AB=2AP=.
故答案为.
【点睛】
本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.
12. 1
【分析】
根据圆心角、弧、弦的关系即可求解.
【详解】
解:是的弦,
,
,
在中,,
,
如图,过点O作OC⊥AB,垂足为C,
又∵∠AOB=90°,OC=AC,
∴OC=AB=1,
即:O点到距离为1,
故答案为:;1.
【点睛】
本题考查了圆心角、弧、弦的关系,本题的解题关键是用勾股定理计算出OA的长,也考查了等腰直角三角形的性质.
13.5cm
【分析】
连接OA,根据垂径定理求出AD,根据勾股定理列式计算即可.
【详解】
解:连接OA,
设⊙O的半径为Rcm,则OD=(R-2)cm,
∵OC⊥AB,
∴AD=DB=AB=4,
在Rt△OAD中,OA2=OD2+AD2,即R2=(R-2)2+42,
解得,R=5,
答:⊙O的半径为5cm.
故答案为:5cm.
【点睛】
本题考查的是垂径定理、勾股定理,掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
14.26
【分析】
连接OA,先根据垂径定理,求出AE的长,再设出圆的半径OA为x,表示出OE,根据勾股定理建立关于x的方程,求出方程的解即可得到x的值即可得到答案.
【详解】
解:连接OA,∵DE⊥AB,且AB=10,
∴AE=BE=5,
设圆O的半径OA的长为x,则OC=OD=x
∵CE=1,
∴OE=x﹣1,
在直角三角形AOC中,根据勾股定理得:
x2﹣(x﹣1)2=52,
解得:x=13,
所以CD=26.
故答案为:26.
【点睛】
此题考查了学生对垂径定理的运用与掌握,注意构建以圆的半径,弦的一半及弦心距的直角三角形是解题关键.
15.
【分析】
连接OB,在Rt△OBC中,根据勾股定理即可求得半径.
【详解】
垂直平分,
的圆心在上,
设的圆心为,连接,设
,
在中,
解得
故答案为:.
【点睛】
本题考查了垂径定理,勾股定理,掌握垂径定理是解题的关键.
16.(0,3)
【分析】
过点A作AH⊥MN,得到H点坐标,根据垂径定理得到HM=HN,故可求出M的坐标,再根据勾股定理求出半径即可.
【详解】
过点A作AH⊥MN,
∵A(1,1),N(0,-1),
∴H(0,1),HN=2
∵MN是的一条弦,AH⊥MN,
∴HM=HN=2,
∴M(0,3)
∵AH=1,HN=2
∴的半径AN=
故答案为:(0,3);.
【点睛】
此题主要考查垂径定理的运用,解题的关键是根据题意作出辅助线求解.
17.半径约为.
【分析】
设圆的半径为r,由垂径定理推论可得:∠OCA=90°,然后根据勾股定理列方程求解即可.
【详解】
解:如图,连接 由垂径定理推论可得:∠OCA=90°,
设圆的半径为r,则CO=r-0.25,AC=0.36,
OC2+AC2=AO2, 即0.362+(r-0.25)2=r2.
解得:r=0.3842≈0.384.
答:这个车轮的半径为0.384m.
【点睛】
本题考查的是垂径定理及其推论的实际应用,勾股定理的应用,解题的关键是由垂径定理的推论得到:∠OCA=90°.
18..
【分析】
过点作于点,并延长交于点,先计算出,再由,根据垂径定理得,然后根据勾股定理计算出,再利用进行计算即可.
【详解】
解:过点作于点,并延长交于点,如图,
则由题意得,
又,
,
在中,,
.
【点睛】
本题考查了垂径定理的应用:垂径定理的应用很广泛,常见的有:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.
19.13
【分析】
连接OA,设OA=r,则OE=r-1,根据垂径定理得AE=5,在中,根据勾股定理即可得.
【详解】
解:如图所示,连接OA,设OA=r,则OE=r-1,
∵弦与E,AB=10,
∴AE=5,
在中,根据勾股定理,
,
解得,
故半径OC的长为13.
【点睛】
本题考查了垂径定理,勾股定理,解题的关键是掌握垂径定理.
20..
【分析】
利用勾股定理和垂径定理解答.
【详解】
解:如图,∵,拱桥的跨度AB=37.4m,拱高CD=7.2m,
∴AD=AB=18.7m,
∴AD2=OA2 (OC CD)2,即18.72=AO2 (AO 7.2)2,
解得AO≈27.9m.即圆弧半径为27.9m.
答:桥拱所在圆的半径为27.9m.
【点睛】
本题考查了垂径定理和勾股定理,注意数形结合思想与方程思想的应用.
21.(1) ;(2).
【分析】
(1)由为⊙的直径,得出,根据圆角定理即可得到答案;
(2)连接 ,过 作 于 .构成直角三角形,进而求出,根据 角所对应的直角边等于斜边的一半,得出,再根据勾股定理求得出 的长,然后由垂径定理求出的长.
【详解】
(1)解:∵ A,D在⊙ O上, ,
,
,
∴ 在△ ACE中,.
(2)解:连接OC,过O作OH⊥CD于H.
∵ OA=OC,∠A=45°,
∴ ∠ACO=∠A=45°.
∴ ∠AOC=90°.
∵ Rt△AOC中,,AC=12,
∴ .
∵ ∠ACD=75°,
∴ .
∴ .
∴ Rt△OCH中,.
∵ OH⊥CD于H,
∴ .
【点睛】
本题主要考查了垂径定理,勾股定理等几何知识点及其应用问题;解题的关键是灵活运用垂径定理,勾股定理等几何知识点来分析,判断,解答.
22.(1)5;(2)
【分析】
(1)连接OB,设半径为r,则OE=r﹣2,构建方程即可解决问题.
(2)根据S△BCO=BC OF=OC BE,求解即可.
【详解】
解:(1)连接OB,设半径为r,则OE=r﹣2,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,
∴BE=DE=4,
在Rt△OBE中,∵OE2+BE2=OB2 ,
∴(r﹣2)2+42=r2
∴r=5
(2)∵r=5,
∴AC=10,EC=8,BE=DE=4cm,
∴BC==4(cm)
∵OF⊥BC,
∴S△BCO=BC OF=OC BE
∴4×OF=5×4,
∴OF=.
【点睛】本题考查了垂径定理和勾股定理,解题的关键是熟记垂径定理和构造△OBE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版2021年九年级上册:24.1.2 垂直于直径的弦 同步练习题
一、选择题
1.上体育课时,老师在运动场上教同学们学习掷铅球,训练时,李力同学掷出的铅球在场地上砸出了一个坑口直径约为10cm,深约为2cm的小坑,则该铅球的直径约为( )
A.20cm B.19.5cm C.14.5cm D.10cm
2.“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是( )
A.12寸 B.24寸 C.13寸 D.26寸
3.如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( )
A.50m B.45m C.40m D.60m
4.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽,则水的最大深度为( )
A.8cm B.10cm C.14cm D.16cm
5.如图,在半径为的⊙O中,弦AB,CD互相垂直,垂足为点P.若AB=CD=8,则OP的长为( )
A. B.
C.4 D.2
6.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )
A.10cm B.10cm C.10cm D.8cm
7.如图,OA为⊙O的半径,弦BC⊥OA于点P.若BC=8,AP=2,则⊙O的半径长为( )
A.5 B.6 C.10 D.
8.如图,在⊙O中,半径r=5,弦AB=8,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
A.2个 B.5个 C.4个 D.3个
二、填空题
9.如图,的直径为,弦长为,点在上运动,则的最小值是____.
10.已知:如图,AB是⊙O的弦,半径OC交弦AB于点P,且AB=10cm,PB=4cm,PC=2cm,则圆心O 到AB的距离为______cm.
11.如图,以点O为圆心的两个同心圆的半径分别等于3和6,大圆的弦AB是小圆的切线,则________.
12.如图为的弦,,则__________,O点到距离=________.
13.如图,⊙O的弦AB=8cm,DC=2cm,直径CE⊥AB于D,半径OC的长为 ___.
14.如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,则直径CD=__________.
15.数学活动课上,同学们想测出一个残损轮子的半径,小聪的解决方案如下:在轮子圆弧上任取两点,,连接,再作出的垂直平分线,交于点,交于点,测出,的长度,即可计算得出轮子的半径.现测出cm,cm,则轮子的半径为__________ cm.
16.已知:如图,与轴交于M、N两点,若A(1,1),N(0,-1),则M点的坐标是___________,的半径是_______.
三、解答题
17.一个残破的车轮如图所示,测得它所剩圆弧两端点间的距离,弧的中点到弧所对弦的距离,如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少?(结果精确到)
18.如图,工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10cm,测得钢珠顶端离零件表面的距离为8cm,则这个小圆孔的宽口AB的长度为多少?
19.如图,CD为的直径,弦于E,如果,,求半径OC的长
20.1400多年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的跨度(即弧所对的弦长)为,拱高(即弧的中点到弦的距离)为,求桥拱所在圆的半径(结果精确到).
21.如图,为⊙的直径,弦与交于点,,.
(1)求的度数;
(2)若,求的长.
22.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,
(1)求⊙O的半径;
(2)求O到弦BC的距离.
参考答案
1.C
【分析】
根据垂径定理,构造直角三角形,小坑的直径就是圆中的弦长,小坑的深就是拱高,利用勾股定理,设出未知数,列出方程,即可求出铅球的直径.
【详解】
解:根据题意,画出图形如图所示,
由题意知,,,是半径,且,
,
设铅球的半径为,则,
在中,根据勾股定理,,
即,
解得:,
所以铅球的直径为:cm,
故选:C.
【点睛】
本题考查的是垂径定理和勾股定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为,弦长为,这条弦的弦心距为,则成立,知道这三个量中的任意两个,就可以求出另外一个.
2.D
【分析】
根据垂径定理和勾股定理求解.
【详解】
解:连接OA,如图所示,
设直径CD的长为2x,则半径OC=x,
∵CD为⊙O的直径,弦AB⊥CD于E,AB=10寸,
∴AE=BE=AB=×10=5寸,
∵OA为⊙O的半径,,则OA=x寸,
根据勾股定理得x2=52+(x-1)2,
解得x=13,
CD=2x=2×13=26(寸).
故选:D.
【点睛】
本题考查了垂径定理和勾股定理.正确的作出辅助线是解题的关键.
3.A
【分析】
设圆弧的圆心为O,过O作OC⊥AB于C,交于D,连接OA,先由垂径定理得AC=BC=AB=150,再由勾股定理求出OC=200,然后求出CD的长即可.
【详解】
解:设圆弧的圆心为O,过O作OC⊥AB于C,交于D,连接OA,如图所示:
则OA=OD=250,AC=BC=AB=150,
∴OC===200(m),
∴CD=OD﹣OC=250﹣200=50(m),
即这些钢索中最长的一根为50m,
故选:A.
【点睛】
本题考查了垂径定理和勾股定理等知识;熟练掌握垂径定理和勾股定理是解题的关键.
4.D
【分析】
连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD的长,进而可得出CD的长.
【详解】
解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,(cm),
∴CD=OC-OD=26-10=16(cm),
故选:D.
【点睛】
本题考查了垂径定理、勾股定理等知识;根据题意作出辅助线,构造出直角三角形是解答此题的关键.
5.B
【分析】
作OM⊥AB于M,ON⊥CD于N,连接OA,OC,根据垂径定理得出BM=AM=4,DN=CN=4,根据勾股定理求出OM和ON,证明四边形OMPN是正方形,即可解决问题.
【详解】
解:如图,作OM⊥AB于M,ON⊥CD于N,连接OA,OC.
∴AM=BM=4,CN=DN=4,
∵OA=OC=2,
∴OM=,
ON=,
∴OM=ON,
∵AB⊥CD,
∴∠OMP=∠ONP=∠MPN=90°,
∴四边形OMPN是矩形,
∵OM=ON,
∴四边形OMPN是正方形,
∴OP=OM=2,
故选:B.
【点睛】
本题考查了垂径定理,勾股定理,正方形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考常考题型.
6.B
【分析】
首先找到EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,设OF=x,则OM是16-x,MF=8,然后在直角三角形MOF中利用勾股定理求得OF的长即可.
【详解】
解:取EF的中点M,作MN⊥AD于点M,
根据垂径定理知球心O在MN上,连接OF,
设OF=x,则OM=16-x,MF=8,
在直角三角形OMF中,OM2+MF2=OF2,
即:(16-x)2+82=x2,
解得:x=10.
即球的半径为10cm.
故选:B.
【点睛】
本题主考查垂径定理及勾股定理的知识,正确作出辅助线构造直角三角形是解题的关键.
7.A
【分析】
连接OB,根据垂径定理和勾股定理列方程即可.
【详解】
解:如图所示,连接OB,
∵,,
∴,,
∵,
∴,
解得,,
则的半径长为,
故选A.
【点睛】
本题考查了垂径定理和勾股定理,解题关键是连接半径,构建直角三角形,列方程解决问题.
8.D
【分析】
当P为AB的中点时OP最短,利用垂径定理得到OP垂直于AB,在直角三角形AOP中,由OA与AP的长,利用勾股定理求出OP的长;当P与A或B重合时,OP最长,求出OP的范围,由OP为整数,即可得到OP所有可能的长.
【详解】
解:当P为AB的中点时,利用垂径定理得到OP⊥AB,此时OP最短,
∵AB=8,∴AP=BP=4,
在直角三角形AOP中,OA=5,AP=4,
根据勾股定理得:OP==,即OP的最小值为3;
当P与A或B重合时,OP最长,此时OP=5,
∴3≤OP<5,
则使线段OP的长度为整数,
∴OP=3,4
根据对称性可知,满足条件的点P的个数有3个
故选:D.
【点睛】
此题考查了垂径定理,以及勾股定理,熟练掌握垂径定理,以及勾股定理是解本题的关键.
9.3
【分析】
根据“点到直线的最短距离是垂线段的长度”知当OP⊥AB时,OP的值最小.连接OA,在直角三角形OAP中由勾股定理即可求得OP的长度.
【详解】
解:当OP⊥AB时,OP的值最小,
则AP′=BP′=AB=4,
如图所示,连接OA,
在Rt△OAP′中,AP′=4,OA=5,
则根据勾股定理知OP′=3,即OP的最小值为3.
【点睛】
本题考查了勾股定理、垂径定理.掌握垂线段最短是解题的关键.
10.
【分析】
过点作于,连接,由垂径定理得,则,设,在和中,由勾股定理得,解得即可,再在中利用勾股定理求出.
【详解】
解:过点作于,连接,如图所示:
则,
,
设,
在和中,
由勾股定理得:,
即,
解得:,
即半径的长为7,
在中,
,
则圆心O到AB的距离为,
故答案是:.
【点睛】
本题考查了垂径定理、勾股定理,解题的关键是熟练掌握垂径定理,由勾股定理得出方程,再求解.
11.
【分析】
连结OP、OA,如图,根据切线的性质得OP⊥AB,再根据垂径定理得到AP=BP,然后在Rt△AOP中,利用勾股定理可计算出AP=,再利用AB=2AP进行计算即可.
【详解】
解:连接OP、OA,如图,
∵大圆的弦AB是小圆的切线,点P为切点,
∴OP⊥AB,
∴AP=BP,
在Rt△AOP中,∵OP=3,OA=6,
∴AP=,
∴AB=2AP=.
故答案为.
【点睛】
本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.
12. 1
【分析】
根据圆心角、弧、弦的关系即可求解.
【详解】
解:是的弦,
,
,
在中,,
,
如图,过点O作OC⊥AB,垂足为C,
又∵∠AOB=90°,OC=AC,
∴OC=AB=1,
即:O点到距离为1,
故答案为:;1.
【点睛】
本题考查了圆心角、弧、弦的关系,本题的解题关键是用勾股定理计算出OA的长,也考查了等腰直角三角形的性质.
13.5cm
【分析】
连接OA,根据垂径定理求出AD,根据勾股定理列式计算即可.
【详解】
解:连接OA,
设⊙O的半径为Rcm,则OD=(R-2)cm,
∵OC⊥AB,
∴AD=DB=AB=4,
在Rt△OAD中,OA2=OD2+AD2,即R2=(R-2)2+42,
解得,R=5,
答:⊙O的半径为5cm.
故答案为:5cm.
【点睛】
本题考查的是垂径定理、勾股定理,掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
14.26
【分析】
连接OA,先根据垂径定理,求出AE的长,再设出圆的半径OA为x,表示出OE,根据勾股定理建立关于x的方程,求出方程的解即可得到x的值即可得到答案.
【详解】
解:连接OA,∵DE⊥AB,且AB=10,
∴AE=BE=5,
设圆O的半径OA的长为x,则OC=OD=x
∵CE=1,
∴OE=x﹣1,
在直角三角形AOC中,根据勾股定理得:
x2﹣(x﹣1)2=52,
解得:x=13,
所以CD=26.
故答案为:26.
【点睛】
此题考查了学生对垂径定理的运用与掌握,注意构建以圆的半径,弦的一半及弦心距的直角三角形是解题关键.
15.
【分析】
连接OB,在Rt△OBC中,根据勾股定理即可求得半径.
【详解】
垂直平分,
的圆心在上,
设的圆心为,连接,设
,
在中,
解得
故答案为:.
【点睛】
本题考查了垂径定理,勾股定理,掌握垂径定理是解题的关键.
16.(0,3)
【分析】
过点A作AH⊥MN,得到H点坐标,根据垂径定理得到HM=HN,故可求出M的坐标,再根据勾股定理求出半径即可.
【详解】
过点A作AH⊥MN,
∵A(1,1),N(0,-1),
∴H(0,1),HN=2
∵MN是的一条弦,AH⊥MN,
∴HM=HN=2,
∴M(0,3)
∵AH=1,HN=2
∴的半径AN=
故答案为:(0,3);.
【点睛】
此题主要考查垂径定理的运用,解题的关键是根据题意作出辅助线求解.
17.半径约为.
【分析】
设圆的半径为r,由垂径定理推论可得:∠OCA=90°,然后根据勾股定理列方程求解即可.
【详解】
解:如图,连接 由垂径定理推论可得:∠OCA=90°,
设圆的半径为r,则CO=r-0.25,AC=0.36,
OC2+AC2=AO2, 即0.362+(r-0.25)2=r2.
解得:r=0.3842≈0.384.
答:这个车轮的半径为0.384m.
【点睛】
本题考查的是垂径定理及其推论的实际应用,勾股定理的应用,解题的关键是由垂径定理的推论得到:∠OCA=90°.
18..
【分析】
过点作于点,并延长交于点,先计算出,再由,根据垂径定理得,然后根据勾股定理计算出,再利用进行计算即可.
【详解】
解:过点作于点,并延长交于点,如图,
则由题意得,
又,
,
在中,,
.
【点睛】
本题考查了垂径定理的应用:垂径定理的应用很广泛,常见的有:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.
19.13
【分析】
连接OA,设OA=r,则OE=r-1,根据垂径定理得AE=5,在中,根据勾股定理即可得.
【详解】
解:如图所示,连接OA,设OA=r,则OE=r-1,
∵弦与E,AB=10,
∴AE=5,
在中,根据勾股定理,
,
解得,
故半径OC的长为13.
【点睛】
本题考查了垂径定理,勾股定理,解题的关键是掌握垂径定理.
20..
【分析】
利用勾股定理和垂径定理解答.
【详解】
解:如图,∵,拱桥的跨度AB=37.4m,拱高CD=7.2m,
∴AD=AB=18.7m,
∴AD2=OA2 (OC CD)2,即18.72=AO2 (AO 7.2)2,
解得AO≈27.9m.即圆弧半径为27.9m.
答:桥拱所在圆的半径为27.9m.
【点睛】
本题考查了垂径定理和勾股定理,注意数形结合思想与方程思想的应用.
21.(1) ;(2).
【分析】
(1)由为⊙的直径,得出,根据圆角定理即可得到答案;
(2)连接 ,过 作 于 .构成直角三角形,进而求出,根据 角所对应的直角边等于斜边的一半,得出,再根据勾股定理求得出 的长,然后由垂径定理求出的长.
【详解】
(1)解:∵ A,D在⊙ O上, ,
,
,
∴ 在△ ACE中,.
(2)解:连接OC,过O作OH⊥CD于H.
∵ OA=OC,∠A=45°,
∴ ∠ACO=∠A=45°.
∴ ∠AOC=90°.
∵ Rt△AOC中,,AC=12,
∴ .
∵ ∠ACD=75°,
∴ .
∴ .
∴ Rt△OCH中,.
∵ OH⊥CD于H,
∴ .
【点睛】
本题主要考查了垂径定理,勾股定理等几何知识点及其应用问题;解题的关键是灵活运用垂径定理,勾股定理等几何知识点来分析,判断,解答.
22.(1)5;(2)
【分析】
(1)连接OB,设半径为r,则OE=r﹣2,构建方程即可解决问题.
(2)根据S△BCO=BC OF=OC BE,求解即可.
【详解】
解:(1)连接OB,设半径为r,则OE=r﹣2,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,
∴BE=DE=4,
在Rt△OBE中,∵OE2+BE2=OB2 ,
∴(r﹣2)2+42=r2
∴r=5
(2)∵r=5,
∴AC=10,EC=8,BE=DE=4cm,
∴BC==4(cm)
∵OF⊥BC,
∴S△BCO=BC OF=OC BE
∴4×OF=5×4,
∴OF=.
【点睛】本题考查了垂径定理和勾股定理,解题的关键是熟记垂径定理和构造△OBE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
