人教版八年级上册 13.3.2等边三角形(第2课时) 教案(表格式)
文档属性
| 名称 | 人教版八年级上册 13.3.2等边三角形(第2课时) 教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 224.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-13 00:00:00 | ||
图片预览

文档简介
轴对称
13.3.2.等边三角形(第2课时)
【教材分析】
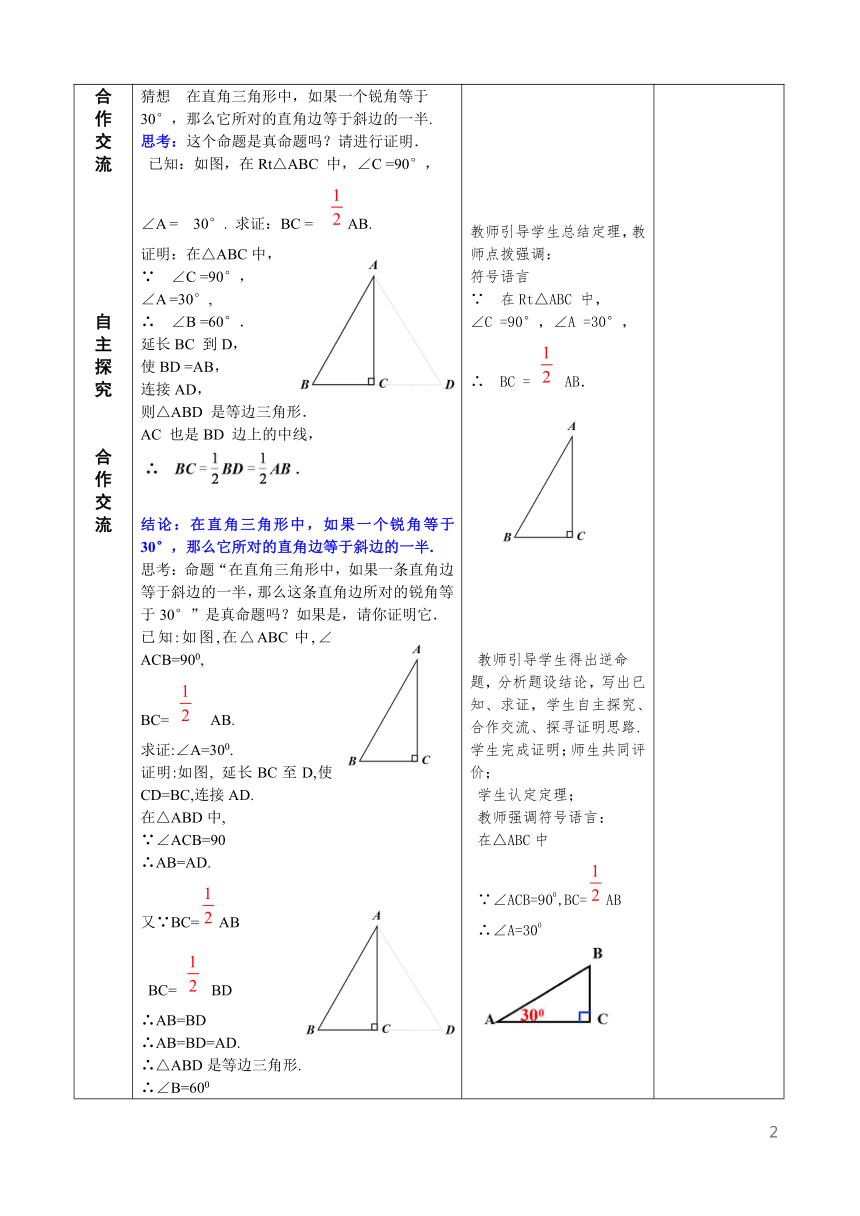
教学目标 知识技能 1.掌握有一个角为30°的直角三角形的性质.2.会用“有一个角为30o的直角三角形的性质”解决有关问题.
过程方法 经历“活动探索一直觉猜想一—推理证明”的过程.培养学生发现问题,解决问题的能力,提高学生的分析能力.
情感态度 体验数学活动中的探索创新、直觉猜想.感受数学推理的严谨性.
重点 有一个角为30o的直角三角形的性质及简单应用
难点 有一个角是30°的直角三角形性质的探索证明过程.
【教学流程】
环节 导 学 问 题 师 生 活 动 二次备课
情境引入 用两个全等的含30°角的直角三角尺,你能拼出怎样的三角形?能拼出等边三角形吗?请说说你的理由. 教师出示问题,引导学生动手拼图;细心观察,自主探究,合作交流,猜想论证
自主探究合作交流自主探究合作交流 探究一、问题 你能借助这个拼成的这个图形,找到含30°角的直角△ABC 的直角边BC 与斜边AB 之间有什么数量关系吗? 如图,△ABC是等边三角形,AC⊥BD于C,则∠BAC=30°,BC=BD=AB.猜想 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.思考:这个命题是真命题吗?请进行证明. 已知:如图,在Rt△ABC 中,∠C =90°,∠A = 30°. 求证:BC = AB.证明:在△ABC中,∵ ∠C =90°,∠A =30°, ∴ ∠B =60°.延长BC 到D,使BD =AB,连接AD,则△ABD 是等边三角形.AC 也是BD 边上的中线,结论:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.思考:命题“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°”是真命题吗?如果是,请你证明它.已知:如图,在△ABC中,∠ACB=900,BC= AB.求证:∠A=300.证明:如图, 延长BC至D,使CD=BC,连接AD.在△ABD中,∵∠ACB=90∴AB=AD.又∵BC=AB BC= BD∴AB=BD∴AB=BD=AD.∴△ABD是等边三角形.∴∠B=600∴∠A=300结论:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°例 如图是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,∠A =30°,问:立柱BC、DE 要多长?分析:观察图形可以发现在Rt△AED与Rt△ACB中,由于∠A=30°,所以DE=AD,BC=AB,又由D是AB的中点,所以DE=AB. 教师提出问题,引导学生自主探究,合作交流,猜想论证,师生共同评价,教师补救;教师引导学生总结定理,教师点拨强调:符号语言∵ 在Rt△ABC 中, ∠C =90°,∠A =30°, ∴ BC = AB. 教师引导学生得出逆命题,分析题设结论,写出已知、求证,学生自主探究、合作交流、探寻证明思路.学生完成证明;师生共同评价;学生认定定理;教师强调符号语言:在△ABC中∵∠ACB=900,BC=AB∴∠A=300教师引导学生分析:思考: 图中BC、DE 分别是哪个直角三角形的直角边?它们所对的锐角分别是多少度?
尝试应用 1.如图,在△ABC中, ∠ACB=90 ° ,∠A=30 °,CD⊥AB,AB=4.则BC = ,BD= . 1题图 2题图2.如图:在Rt△ABC中∠A=300,AB+BC=12cm 则AB=_____cm3.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm,BD=___, BE=_______ 4、已知:如图,在△ABC中,AB=AC=2a,∠ABC=∠ACB=15°,CD是腰AB上的高,求CD的长. 教师出示问题,学生自主完成,学生展示答案,师生共同评价1、2,1;2、8;3、4cm,2cm4.解:∵∠ABC=∠ACB=15°∴∠DAC=∠ABC+∠ACB =15°+15°=30° ∴CD= AC= ×2a= a.
成果展示 (1)本节课学习了哪些内容?(2)在应用含30°角的直角三角形的性质时,能解决哪些问题?需要注意哪些问题? 师引导学生归纳总结.梳理知识,并建立知识体系.
补偿提高 5.要把一块三角形的土地均匀分给甲 、 乙、丙三家农户去种植,如果∠C=90°,∠B=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来. 教师出示问题,学生自主完成,学生展示答案,师生共同评价法一:作斜边AB的垂直平分线DE交AB于D交BC于E;再连接AE即可法二:作∠BAC的平分线AE交BC于E,再作ED⊥AB于D即可
作业设计 必做题 教材第81页练习.选做题 教材第81页习题13.3第15题 学生认定作业,课下独立完成
PAGE
2
13.3.2.等边三角形(第2课时)
【教材分析】
教学目标 知识技能 1.掌握有一个角为30°的直角三角形的性质.2.会用“有一个角为30o的直角三角形的性质”解决有关问题.
过程方法 经历“活动探索一直觉猜想一—推理证明”的过程.培养学生发现问题,解决问题的能力,提高学生的分析能力.
情感态度 体验数学活动中的探索创新、直觉猜想.感受数学推理的严谨性.
重点 有一个角为30o的直角三角形的性质及简单应用
难点 有一个角是30°的直角三角形性质的探索证明过程.
【教学流程】
环节 导 学 问 题 师 生 活 动 二次备课
情境引入 用两个全等的含30°角的直角三角尺,你能拼出怎样的三角形?能拼出等边三角形吗?请说说你的理由. 教师出示问题,引导学生动手拼图;细心观察,自主探究,合作交流,猜想论证
自主探究合作交流自主探究合作交流 探究一、问题 你能借助这个拼成的这个图形,找到含30°角的直角△ABC 的直角边BC 与斜边AB 之间有什么数量关系吗? 如图,△ABC是等边三角形,AC⊥BD于C,则∠BAC=30°,BC=BD=AB.猜想 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.思考:这个命题是真命题吗?请进行证明. 已知:如图,在Rt△ABC 中,∠C =90°,∠A = 30°. 求证:BC = AB.证明:在△ABC中,∵ ∠C =90°,∠A =30°, ∴ ∠B =60°.延长BC 到D,使BD =AB,连接AD,则△ABD 是等边三角形.AC 也是BD 边上的中线,结论:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.思考:命题“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°”是真命题吗?如果是,请你证明它.已知:如图,在△ABC中,∠ACB=900,BC= AB.求证:∠A=300.证明:如图, 延长BC至D,使CD=BC,连接AD.在△ABD中,∵∠ACB=90∴AB=AD.又∵BC=AB BC= BD∴AB=BD∴AB=BD=AD.∴△ABD是等边三角形.∴∠B=600∴∠A=300结论:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°例 如图是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,∠A =30°,问:立柱BC、DE 要多长?分析:观察图形可以发现在Rt△AED与Rt△ACB中,由于∠A=30°,所以DE=AD,BC=AB,又由D是AB的中点,所以DE=AB. 教师提出问题,引导学生自主探究,合作交流,猜想论证,师生共同评价,教师补救;教师引导学生总结定理,教师点拨强调:符号语言∵ 在Rt△ABC 中, ∠C =90°,∠A =30°, ∴ BC = AB. 教师引导学生得出逆命题,分析题设结论,写出已知、求证,学生自主探究、合作交流、探寻证明思路.学生完成证明;师生共同评价;学生认定定理;教师强调符号语言:在△ABC中∵∠ACB=900,BC=AB∴∠A=300教师引导学生分析:思考: 图中BC、DE 分别是哪个直角三角形的直角边?它们所对的锐角分别是多少度?
尝试应用 1.如图,在△ABC中, ∠ACB=90 ° ,∠A=30 °,CD⊥AB,AB=4.则BC = ,BD= . 1题图 2题图2.如图:在Rt△ABC中∠A=300,AB+BC=12cm 则AB=_____cm3.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm,BD=___, BE=_______ 4、已知:如图,在△ABC中,AB=AC=2a,∠ABC=∠ACB=15°,CD是腰AB上的高,求CD的长. 教师出示问题,学生自主完成,学生展示答案,师生共同评价1、2,1;2、8;3、4cm,2cm4.解:∵∠ABC=∠ACB=15°∴∠DAC=∠ABC+∠ACB =15°+15°=30° ∴CD= AC= ×2a= a.
成果展示 (1)本节课学习了哪些内容?(2)在应用含30°角的直角三角形的性质时,能解决哪些问题?需要注意哪些问题? 师引导学生归纳总结.梳理知识,并建立知识体系.
补偿提高 5.要把一块三角形的土地均匀分给甲 、 乙、丙三家农户去种植,如果∠C=90°,∠B=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来. 教师出示问题,学生自主完成,学生展示答案,师生共同评价法一:作斜边AB的垂直平分线DE交AB于D交BC于E;再连接AE即可法二:作∠BAC的平分线AE交BC于E,再作ED⊥AB于D即可
作业设计 必做题 教材第81页练习.选做题 教材第81页习题13.3第15题 学生认定作业,课下独立完成
PAGE
2
