江西省吉安市四校2021-2022学年高二上学期期中考试数学(理)试题(Word版含答案)
文档属性
| 名称 | 江西省吉安市四校2021-2022学年高二上学期期中考试数学(理)试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 659.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-13 13:40:23 | ||
图片预览


文档简介
安福二中、泰和二中、井大附中、吉安县三中、四校联考
高二数学(理)试题(11月1日、2日)
一、选择题(每小题5分,12小题,共60分)
1.在平面直角坐标系中,直线的倾斜角是( )
A. B. C. D.
2.已知m,n是两条不同的直线,,是两个不同的平面,则下列命题正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
3.已知m,,若两条平行直线与之间的距离是,则( )
A.0 B.1 C.-2 D.-1
4.点关于直线的对称点为( )
A. B. C. D.
5.已知长方体全部棱长的和为36,表面积为5,则其体对角线的长为( )
A.4 B. C. D.
6.点与圆上任一点连线的中点轨迹方程是( )
A. B.
C. D.
7.陀螺是中国民间最早的娱乐工具之一,也称陀罗.如图,网格纸上小正方形的边长为1,粗线画出的是某个陀螺的三视图,则该陀螺的表面积为( )
A. B.
C. D.
8.已知A,B,C,D是同一球面上的四个点,其中是正三角形,平面,,则该球的体积为( )
A. B. C. D.
9.平面内与点距离为3,且与点距离为2的直线的条数为( )
A.4 B.3 C.2 D.1
10.已知两点,,若直线上至少存在三个点P,使得是直角三角形,则实数k的取值范围是( )
A. B. C. D.
11.如图,在四棱锥中,底面为正方形,且,其中E,M,N分别是,,的中点,动点P在线段上运动时,下列四个结论:
①;②;③面;④面;
其中恒成立的为( )
A.①③ B.③④ C.①④ D.②③
12.在棱长为1的正方体中,点E,F分别是棱,的中点,P是上底面内一点,若平面,则线段长度的取值范围是( )
A. B. C. D.
二、填空题(每小题5分,4小题,共20分)
13.一个三角形用斜二测画法画出来的直观图是边长为2的正三角形,则原三角形的面积是________.
14.设是空间直角坐标系中的一点,则点关于坐标平面的对称点的坐标是________.
15.已知直线与圆,则圆C上各点到l的距离的最小值为________.
16.已知三棱锥中,棱,,的中点分别是M,N,O,,,都是正三角形,则异面直线与所成角的余弦值为________.
三、解答题(第17题10分,其他每题12分,共70分)
17.已知直线和直线.
(1)当时,若,求实数a的值;
(2)若,求的最小值.
18.已知的顶点,直线的方程为,边上的高所在直线的方程为.
(1)求顶点A和B的坐标;
(2)求的外接圆的一般方程.
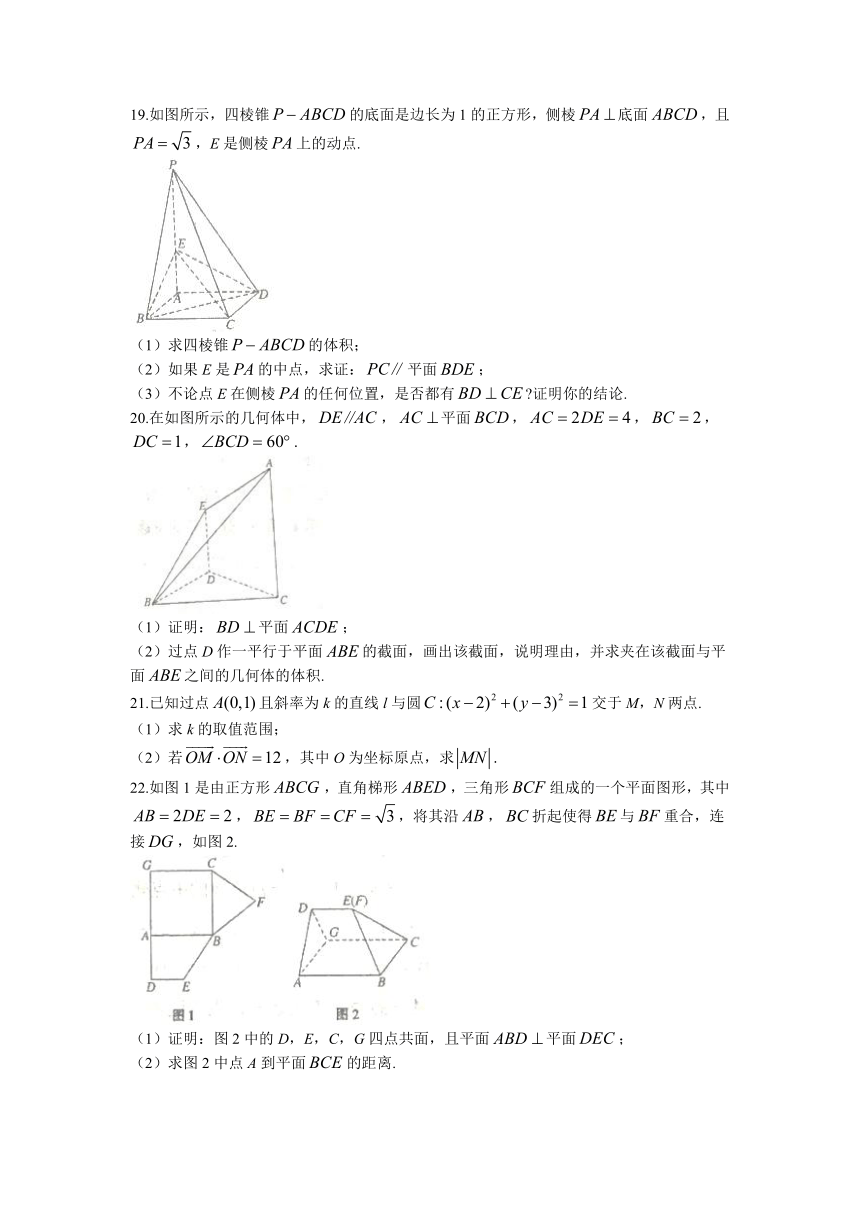
19.如图所示,四棱锥的底面是边长为1的正方形,侧棱底面,且,E是侧棱上的动点.
(1)求四棱锥的体积;
(2)如果E是的中点,求证:平面;
(3)不论点E在侧棱的任何位置,是否都有 证明你的结论.
20.在如图所示的几何体中,,平面,,,,.
(1)证明:平面;
(2)过点D作一平行于平面的截面,画出该截面,说明理由,并求夹在该截面与平面之间的几何体的体积.
21.已知过点且斜率为k的直线l与圆交于M,N两点.
(1)求k的取值范围;
(2)若,其中O为坐标原点,求.
22.如图1是由正方形,直角梯形,三角形组成的一个平面图形,其中,,将其沿,折起使得与重合,连接,如图2.
(1)证明:图2中的D,E,C,G四点共面,且平面平面;
(2)求图2中点A到平面的距离.
理科数学试题答案及评分标准
一、选择题(每题5分,12个小题,共60分)
1 2 3 4 5 6 7 8 9 10 11 12
B A C B D A C A B D C B
二、填空题(每题5分,4个小题,共20分)
13. 14. 15. 16.
三、解答题(17题10分,其他每题12分,共70分)
17:(1)因为直线和直线,,
所以,且,即,且.
若,则,整理,得,解得.
(2)若,当任一直线斜率不存在时,显然不成立,
所以,所以,所以
又因为,所以,当且仅当,即时等号成立
所以,则的最小值为2.
18.(1)由解得所以顶点.
因为,,所以设直线的方程为,
将代入,得.联立解得
所以顶点,所以顶点A和B的坐标分别为和.
(2)设的外接圆方程为,
将,和三点的坐标分别代入,
得解得
所以的外接圆的一般方程为.
19.(1)因为平面,
所以,
即四棱锥的体积为
(2)证明:如图所示,连接交于点O,连接.
因为四边形是正方形,所以O是的中点,
又E是的中点,所以,
因为平面,平面,
所以平面.
(3)不论点E在侧棱的任何位置,都有.证明如下:
因为四边形是正方形,所以,
因为底面,且平面,所以,
又,所以平面.
因为不论点E在侧棱的任何位置,都有平面,
所以不论点E在侧棱的任何位置,都有.
20.解析:(1)在中,由余弦定理得,
所以,所以为直角三角形,.
因为平面,所以.
而,所以平面.
(2)如图,取的中点,的中点,连接,,,则平面即所求.
理由如下:因为,,所以四边形为平行四边形,
所以,从而平面,
易证平面.
因为,所以平面平面.
由(1)可知,平面,平面.
,
,
所以所求几何体的体积.
21.(1)由题设,可知直线的方程为.
因为直线l与圆C交于两点,所以.
解得.
所以k的取值范围为.
(2)设,.
将代入圆的方程,整理得
.
所以,.
.
由题设可得,解得,所以l的方程为
故圆C的圆心在l上,所以.
22.解析:(1)证明:因为正方形中,,梯形中,,
所以,所以D,E,C,G四点共面.
因为,所以.因为,,
所以平面.
因为平面,所以.
在直角梯形中,,,,可求得,
同理在直角梯形中,可求得,又,
所以,由勾股定理的逆定理可知
因为,,所以平面.
因为平面,故平面平面,即平面平面.
(2)在等腰直角三角形中,边上的高为1,所以点D到平面的距离等于1.
因为与平面平行,所以点E到平面的距离,
连接,,三角形的面积,
中,边上的高为高为,
的面积.
设点A到平面的距离为,由三棱锥的体积,
得,故点A到平面的距离为.
高二数学(理)试题(11月1日、2日)
一、选择题(每小题5分,12小题,共60分)
1.在平面直角坐标系中,直线的倾斜角是( )
A. B. C. D.
2.已知m,n是两条不同的直线,,是两个不同的平面,则下列命题正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
3.已知m,,若两条平行直线与之间的距离是,则( )
A.0 B.1 C.-2 D.-1
4.点关于直线的对称点为( )
A. B. C. D.
5.已知长方体全部棱长的和为36,表面积为5,则其体对角线的长为( )
A.4 B. C. D.
6.点与圆上任一点连线的中点轨迹方程是( )
A. B.
C. D.
7.陀螺是中国民间最早的娱乐工具之一,也称陀罗.如图,网格纸上小正方形的边长为1,粗线画出的是某个陀螺的三视图,则该陀螺的表面积为( )
A. B.
C. D.
8.已知A,B,C,D是同一球面上的四个点,其中是正三角形,平面,,则该球的体积为( )
A. B. C. D.
9.平面内与点距离为3,且与点距离为2的直线的条数为( )
A.4 B.3 C.2 D.1
10.已知两点,,若直线上至少存在三个点P,使得是直角三角形,则实数k的取值范围是( )
A. B. C. D.
11.如图,在四棱锥中,底面为正方形,且,其中E,M,N分别是,,的中点,动点P在线段上运动时,下列四个结论:
①;②;③面;④面;
其中恒成立的为( )
A.①③ B.③④ C.①④ D.②③
12.在棱长为1的正方体中,点E,F分别是棱,的中点,P是上底面内一点,若平面,则线段长度的取值范围是( )
A. B. C. D.
二、填空题(每小题5分,4小题,共20分)
13.一个三角形用斜二测画法画出来的直观图是边长为2的正三角形,则原三角形的面积是________.
14.设是空间直角坐标系中的一点,则点关于坐标平面的对称点的坐标是________.
15.已知直线与圆,则圆C上各点到l的距离的最小值为________.
16.已知三棱锥中,棱,,的中点分别是M,N,O,,,都是正三角形,则异面直线与所成角的余弦值为________.
三、解答题(第17题10分,其他每题12分,共70分)
17.已知直线和直线.
(1)当时,若,求实数a的值;
(2)若,求的最小值.
18.已知的顶点,直线的方程为,边上的高所在直线的方程为.
(1)求顶点A和B的坐标;
(2)求的外接圆的一般方程.
19.如图所示,四棱锥的底面是边长为1的正方形,侧棱底面,且,E是侧棱上的动点.
(1)求四棱锥的体积;
(2)如果E是的中点,求证:平面;
(3)不论点E在侧棱的任何位置,是否都有 证明你的结论.
20.在如图所示的几何体中,,平面,,,,.
(1)证明:平面;
(2)过点D作一平行于平面的截面,画出该截面,说明理由,并求夹在该截面与平面之间的几何体的体积.
21.已知过点且斜率为k的直线l与圆交于M,N两点.
(1)求k的取值范围;
(2)若,其中O为坐标原点,求.
22.如图1是由正方形,直角梯形,三角形组成的一个平面图形,其中,,将其沿,折起使得与重合,连接,如图2.
(1)证明:图2中的D,E,C,G四点共面,且平面平面;
(2)求图2中点A到平面的距离.
理科数学试题答案及评分标准
一、选择题(每题5分,12个小题,共60分)
1 2 3 4 5 6 7 8 9 10 11 12
B A C B D A C A B D C B
二、填空题(每题5分,4个小题,共20分)
13. 14. 15. 16.
三、解答题(17题10分,其他每题12分,共70分)
17:(1)因为直线和直线,,
所以,且,即,且.
若,则,整理,得,解得.
(2)若,当任一直线斜率不存在时,显然不成立,
所以,所以,所以
又因为,所以,当且仅当,即时等号成立
所以,则的最小值为2.
18.(1)由解得所以顶点.
因为,,所以设直线的方程为,
将代入,得.联立解得
所以顶点,所以顶点A和B的坐标分别为和.
(2)设的外接圆方程为,
将,和三点的坐标分别代入,
得解得
所以的外接圆的一般方程为.
19.(1)因为平面,
所以,
即四棱锥的体积为
(2)证明:如图所示,连接交于点O,连接.
因为四边形是正方形,所以O是的中点,
又E是的中点,所以,
因为平面,平面,
所以平面.
(3)不论点E在侧棱的任何位置,都有.证明如下:
因为四边形是正方形,所以,
因为底面,且平面,所以,
又,所以平面.
因为不论点E在侧棱的任何位置,都有平面,
所以不论点E在侧棱的任何位置,都有.
20.解析:(1)在中,由余弦定理得,
所以,所以为直角三角形,.
因为平面,所以.
而,所以平面.
(2)如图,取的中点,的中点,连接,,,则平面即所求.
理由如下:因为,,所以四边形为平行四边形,
所以,从而平面,
易证平面.
因为,所以平面平面.
由(1)可知,平面,平面.
,
,
所以所求几何体的体积.
21.(1)由题设,可知直线的方程为.
因为直线l与圆C交于两点,所以.
解得.
所以k的取值范围为.
(2)设,.
将代入圆的方程,整理得
.
所以,.
.
由题设可得,解得,所以l的方程为
故圆C的圆心在l上,所以.
22.解析:(1)证明:因为正方形中,,梯形中,,
所以,所以D,E,C,G四点共面.
因为,所以.因为,,
所以平面.
因为平面,所以.
在直角梯形中,,,,可求得,
同理在直角梯形中,可求得,又,
所以,由勾股定理的逆定理可知
因为,,所以平面.
因为平面,故平面平面,即平面平面.
(2)在等腰直角三角形中,边上的高为1,所以点D到平面的距离等于1.
因为与平面平行,所以点E到平面的距离,
连接,,三角形的面积,
中,边上的高为高为,
的面积.
设点A到平面的距离为,由三棱锥的体积,
得,故点A到平面的距离为.
同课章节目录
