5.6.2函数y=Asin(ωx+φ)的图像 同步练习——2021-2022学年高一上学期数学人教A版(2019)必修第一册(Word含答案解析)
文档属性
| 名称 | 5.6.2函数y=Asin(ωx+φ)的图像 同步练习——2021-2022学年高一上学期数学人教A版(2019)必修第一册(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 820.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 15:52:25 | ||
图片预览




文档简介
一、单选题
1.将函数的图象向左平移个单位后,所得图象对应的函数是( )
A. B.
C. D.
2.将函数的图象向左平移个单位长度后得到曲线,再将上所有点的横坐标伸长到原来的2倍得到曲线,则的解析式为( )
A. B.
C. D.
3.将函数的图象向左平移个单位长度,得到函数的图象,若函数为奇函数,则的最小值是( )
A. B. C. D.
4.已知曲线C1:y = cosx,C2∶,则下面结论正确的是( )
A.把C1上各点的横坐标伸长到原来的2倍纵坐标不变,再把所得曲线向左平移个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把所得曲线向左平移个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把所得曲线向左平移个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把所得曲线向左平移个单位长度,得到曲线C2
5.下图是函数,的一部分图像,此函数的解析式是( )
A. B.
C. D.
6.已知函数(,)的最小正周期是,将的图象向左平移个单位长度后所得的函数图象过点,则关于函数的说法不正确的是( )
A.是函数一条对称轴
B.是函数一个对称中心
C.在区间上单调递增
D.在区间上单调递减
7.已知函数的部分图象如图所示,则( )
A. B.
C. D.
8.已知,为函数的图象与轴的两个相邻交点的横坐标,将的图象向左平移个单位得到的图象,,,为两个函数图象的交点,则面积的最小值为( ).
A. B. C. D.
二、多选题
9.(多选)要得到函数的图象,只要将函数的图象( )
A.每一点的横坐标扩大到原来的倍(纵坐标不变),再将所得图象向左平移个单位长度
B.每一点的横坐标缩短到原来的 (纵坐标不变),再将所得图象向左平移个单位长度
C.向左平移个单位长度,再将所得图象每一点的横坐标缩短到原来的 (纵坐标不变)
D.向左平移个单位长度,再将所得图象每一点的横坐标缩短到原来的 (纵坐标不变)
10.将函数的图像向左平移个单位后,得到函数的图像,则下列结论中正确的是( )
A.
B.的图象关于点中心对称
C.的图象关于对称
D.在区间上单调递增
11.如图所示,函数,的部分图象与坐标轴分别交于点,,,且的面积为,以下结论正确的是( )
A.点的纵坐标为
B.是的一个单调递增区间
C.对任意,点都是图象的对称中心
D.的图象可由图象上各点的横坐标缩短为原来的倍,纵坐标不变,再把得到的图象向左平移个单位得到
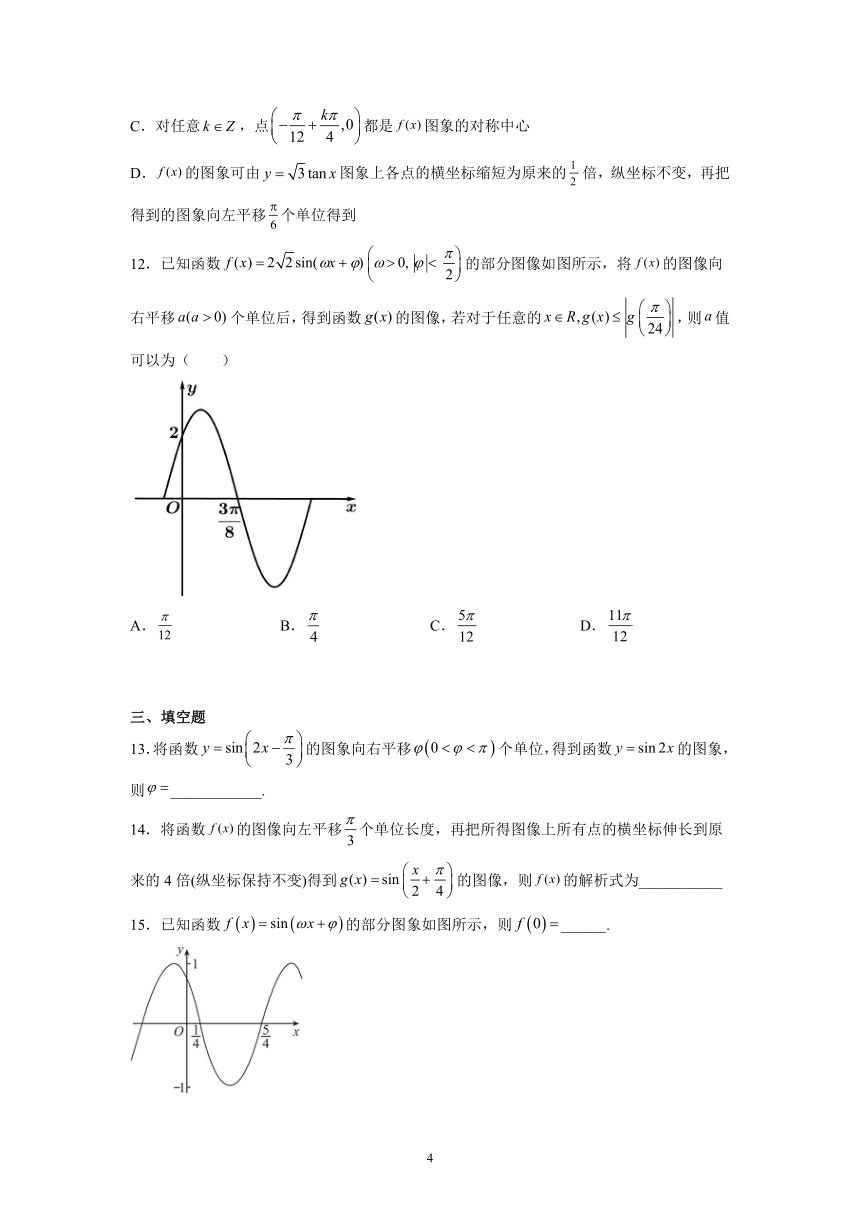
12.已知函数的部分图像如图所示,将的图像向右平移个单位后,得到函数的图像,若对于任意的,则值可以为( )
A. B. C. D.
三、填空题
13.将函数的图象向右平移个单位,得到函数的图象,则____________.
14.将函数的图像向左平移个单位长度,再把所得图像上所有点的横坐标伸长到原来的4倍(纵坐标保持不变)得到的图像,则的解析式为___________
15.已知函数的部分图象如图所示,则______.
16.已知函数,将的图象向左平移个单位长度,得到的图象,给出以下四个结论:
①函数为偶函数;
②方程在区间上有个实根;
③函数在区间上单调递减;
④函数的值域为.
其中所有错误结论的序号是___________.
四、解答题
17.(1)利用“五点法”画出函数在长度为一个周期的闭区间的简图.
列表:
x
y
作图:
(2)并说明该函数图象可由的图象经过怎么变换得到的.
(3)求函数图象的对称轴方程.
18.已知函数(,,)的部分图象如图所示.
(1)求的解析式和对称中心坐标;
(2)将的图象向左平移个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数的图象,求函数在上的最值及对应的的值.
19.在下列三个条件中任选一个,补充在下面的问题中,并作答.
①的最小正周期为,且是偶函数;
②图象上相邻两个最高点之间的距离为,且;
③直线与直线是图象上相邻的两条对称轴,且.
问题:已知函数,若______.
(1)求,的值;
(2)将函数的图象向右平移个单位长度后,再将得到的函数图象上所有点的横坐标伸长为原来的4倍,纵坐标不变,得到函数的图象,求在上的单调递减区间.
20.如图所示,某小区为美化环境,准备在小区内的草坪的一侧修建一条直路OC,另一侧修建一条休闲大道.休闲大道的前一段OD是函数的图象的一部分,后一段DBC是函数(,,,)的图象,图象的最高点为,且,垂足为点F.
(1)求函数()的解析式;
(2)若在草坪内修建如图所示的矩形儿童乐园PMFE,点P在曲线OD上,其横坐标为,点E在OC上,求儿童乐园的面积.
参考答案
1.C
2.A
3.A
4.C
5.C
由图像可知,最小正周期,所以可取,所以,
又因为图像经过点,所以,所以,
所以,所以,所以可取,
此时函数的解析式为,
故选:C.
6.D
,向左平移个单位长度后所得到的函数是,
其中图象过,所以,因为,,
所以.
因为,所以是函数一条对称轴,故A正确
因为,所以是函数一个对称中心,故B正确
当时,,所以在区间上单调递增,故C正确
当时,,所以在区间上不单调递减,故D错误
故选:D
7.C
由的图象可知,,,故,
又且,则可得出,故.
又根据函数的对称性可知,
,
所以,
所以
.
故选:C.
8.B
∵,∴.
将代入,得.
又∵,∴,∴.
∵,
由,得,
∴.∵相邻两个交点的横坐标之差为,
将代入,得到交点的纵坐标为,
∴面积的最小值为.
故选:B.
9.BC
(1)先伸缩后平移时:每一点的横坐标缩短到原来的 (纵坐标不变),再将所得图象向左平移个单位长度,所以A选项错误,B选项正确.
(2)先平移后伸缩时:向左平移个单位长度,再将所得图象每一点的横坐标缩短到原来的 (纵坐标不变),所以C选项正确,D选项错误.
故选:BC.
10.BCD
,故A错误;
令可得,故B正确;
令可得,故C正确;
,所以,
易知在单增,所以在单增,故D正确.
故选:BCD
11.BC
解:因为,所以最小正周期,即,又的面积为,所以,所以,即的纵坐标为,故A错误;
因为,所以,所以,因为
所以,所以,令,,解得,,所以函数的单调递增区间为,,故B正确;
令,,解得,,所以函数的对称中心为,,故C正确;
将图象上各点的横坐标缩短为原来的倍,得到,再将函数向左平移个单位,得到,故D错误;
故选:BC
12.CD
解:由函数的图像可知,的图像过点,
所以,可得,
因为,所以,
因为的图像过点,
所以,解得,
所以,
因为,所以不妨设,则可得,
所以,
因为,
所以,
因为对于任意的,
所以,
所以,
所以,
当时,,
当时,,
故选:CD
13.
将函数的图象向右平移个单位,
得到,
因为,
所以,,即,.
又因为,所以.
故答案为:
14.
解:将图像上所有点的横坐标缩短为原来的(纵坐标保持不变),得到,再将的图像向右平移个单位长度得到.
故答案为:
15.
由题意可得,可得,则,所以
则
由,所以
则,所以
所以
故答案为:
16.②④
将函数的图象向左平移个单位长度,得到的图象,
所以.
函数的定义域为,,
所以函数为偶函数,所以①正确;
,,
所以当时,,所以当时,与的图象有无数个交点,所以方程在区间上有无数个实根,所以②不正确;
因为,
作出函数的部分图象如图所示,
所以函数的单调递减区间为和,所以③正确;
函数的值域与的值域相同,均为,所以④不正确.
故答案为:②④.
17.(1)见解析(2) 见解析(3) .
解:(1)先列表,后描点并画图
0
x
y 0 1 0 -1 0
;
(2)把的图象上所有的点向左平移个单位, 再把所得图象的点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象,即的图象;
(3)由,
所以函数的对称轴方程是.
18.(1),对称中心的坐标为,;(2)时,取得最小值;时,取得最大值.
解:(1)由图象可知,可得:,,
又由于,可得:,所以,
由图象及五点法作图可知:,所以,
所以.
令,,得,,
所以的对称中心的坐标为,.
(2)将的图象向左平移个单位,得到;
再将横坐标伸长到原来的2倍,纵坐标不变,得到;
将图象向上平移1个单位,得到,
即,
因为,所以,
所以当,即时,取得最小值,
当,即时,取得最大值.
19.
(1),
(2)
(1)
选条件①:(1)∵的最小正周期为,
∴,∴.又是偶函数,∴对恒成立,∴对恒成立,
∴,∴.又,∴.
选条件②:∵函数图象上相邻两个最高点之间的距离为,
∴,∴.
又,∴,即,
∴,
又,∴.
选条件③:∵直线与直线是图象上相邻的两条对称轴,
∴,即,∴.
又.∴,∴,又,∴.
(2)
由(1)无论选择①②③均有,,,
将的图象向右平移个单位长度后,得到的图象,
将的图象上所有点的横坐标伸长为原来的4倍,
纵坐标不变,得到的图象.
由,
得,
∵,∴,
∴在上的单调递减区间是.
20.
(1),
(2)
解:(1)
由题意可知,,
不妨设最小正周期为,
由图像知,,即,则,
∵点在的图象上,
∴,,即,.
∵,∴,
故,.
(2)
在中,令,则,故点坐标为,
将代入,解得,,
从而曲线OD的方程为:,
当时,则,故点坐标为,
∴矩形PMFE的面积为,
即儿童乐园的面积为.
1.将函数的图象向左平移个单位后,所得图象对应的函数是( )
A. B.
C. D.
2.将函数的图象向左平移个单位长度后得到曲线,再将上所有点的横坐标伸长到原来的2倍得到曲线,则的解析式为( )
A. B.
C. D.
3.将函数的图象向左平移个单位长度,得到函数的图象,若函数为奇函数,则的最小值是( )
A. B. C. D.
4.已知曲线C1:y = cosx,C2∶,则下面结论正确的是( )
A.把C1上各点的横坐标伸长到原来的2倍纵坐标不变,再把所得曲线向左平移个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把所得曲线向左平移个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把所得曲线向左平移个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把所得曲线向左平移个单位长度,得到曲线C2
5.下图是函数,的一部分图像,此函数的解析式是( )
A. B.
C. D.
6.已知函数(,)的最小正周期是,将的图象向左平移个单位长度后所得的函数图象过点,则关于函数的说法不正确的是( )
A.是函数一条对称轴
B.是函数一个对称中心
C.在区间上单调递增
D.在区间上单调递减
7.已知函数的部分图象如图所示,则( )
A. B.
C. D.
8.已知,为函数的图象与轴的两个相邻交点的横坐标,将的图象向左平移个单位得到的图象,,,为两个函数图象的交点,则面积的最小值为( ).
A. B. C. D.
二、多选题
9.(多选)要得到函数的图象,只要将函数的图象( )
A.每一点的横坐标扩大到原来的倍(纵坐标不变),再将所得图象向左平移个单位长度
B.每一点的横坐标缩短到原来的 (纵坐标不变),再将所得图象向左平移个单位长度
C.向左平移个单位长度,再将所得图象每一点的横坐标缩短到原来的 (纵坐标不变)
D.向左平移个单位长度,再将所得图象每一点的横坐标缩短到原来的 (纵坐标不变)
10.将函数的图像向左平移个单位后,得到函数的图像,则下列结论中正确的是( )
A.
B.的图象关于点中心对称
C.的图象关于对称
D.在区间上单调递增
11.如图所示,函数,的部分图象与坐标轴分别交于点,,,且的面积为,以下结论正确的是( )
A.点的纵坐标为
B.是的一个单调递增区间
C.对任意,点都是图象的对称中心
D.的图象可由图象上各点的横坐标缩短为原来的倍,纵坐标不变,再把得到的图象向左平移个单位得到
12.已知函数的部分图像如图所示,将的图像向右平移个单位后,得到函数的图像,若对于任意的,则值可以为( )
A. B. C. D.
三、填空题
13.将函数的图象向右平移个单位,得到函数的图象,则____________.
14.将函数的图像向左平移个单位长度,再把所得图像上所有点的横坐标伸长到原来的4倍(纵坐标保持不变)得到的图像,则的解析式为___________
15.已知函数的部分图象如图所示,则______.
16.已知函数,将的图象向左平移个单位长度,得到的图象,给出以下四个结论:
①函数为偶函数;
②方程在区间上有个实根;
③函数在区间上单调递减;
④函数的值域为.
其中所有错误结论的序号是___________.
四、解答题
17.(1)利用“五点法”画出函数在长度为一个周期的闭区间的简图.
列表:
x
y
作图:
(2)并说明该函数图象可由的图象经过怎么变换得到的.
(3)求函数图象的对称轴方程.
18.已知函数(,,)的部分图象如图所示.
(1)求的解析式和对称中心坐标;
(2)将的图象向左平移个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数的图象,求函数在上的最值及对应的的值.
19.在下列三个条件中任选一个,补充在下面的问题中,并作答.
①的最小正周期为,且是偶函数;
②图象上相邻两个最高点之间的距离为,且;
③直线与直线是图象上相邻的两条对称轴,且.
问题:已知函数,若______.
(1)求,的值;
(2)将函数的图象向右平移个单位长度后,再将得到的函数图象上所有点的横坐标伸长为原来的4倍,纵坐标不变,得到函数的图象,求在上的单调递减区间.
20.如图所示,某小区为美化环境,准备在小区内的草坪的一侧修建一条直路OC,另一侧修建一条休闲大道.休闲大道的前一段OD是函数的图象的一部分,后一段DBC是函数(,,,)的图象,图象的最高点为,且,垂足为点F.
(1)求函数()的解析式;
(2)若在草坪内修建如图所示的矩形儿童乐园PMFE,点P在曲线OD上,其横坐标为,点E在OC上,求儿童乐园的面积.
参考答案
1.C
2.A
3.A
4.C
5.C
由图像可知,最小正周期,所以可取,所以,
又因为图像经过点,所以,所以,
所以,所以,所以可取,
此时函数的解析式为,
故选:C.
6.D
,向左平移个单位长度后所得到的函数是,
其中图象过,所以,因为,,
所以.
因为,所以是函数一条对称轴,故A正确
因为,所以是函数一个对称中心,故B正确
当时,,所以在区间上单调递增,故C正确
当时,,所以在区间上不单调递减,故D错误
故选:D
7.C
由的图象可知,,,故,
又且,则可得出,故.
又根据函数的对称性可知,
,
所以,
所以
.
故选:C.
8.B
∵,∴.
将代入,得.
又∵,∴,∴.
∵,
由,得,
∴.∵相邻两个交点的横坐标之差为,
将代入,得到交点的纵坐标为,
∴面积的最小值为.
故选:B.
9.BC
(1)先伸缩后平移时:每一点的横坐标缩短到原来的 (纵坐标不变),再将所得图象向左平移个单位长度,所以A选项错误,B选项正确.
(2)先平移后伸缩时:向左平移个单位长度,再将所得图象每一点的横坐标缩短到原来的 (纵坐标不变),所以C选项正确,D选项错误.
故选:BC.
10.BCD
,故A错误;
令可得,故B正确;
令可得,故C正确;
,所以,
易知在单增,所以在单增,故D正确.
故选:BCD
11.BC
解:因为,所以最小正周期,即,又的面积为,所以,所以,即的纵坐标为,故A错误;
因为,所以,所以,因为
所以,所以,令,,解得,,所以函数的单调递增区间为,,故B正确;
令,,解得,,所以函数的对称中心为,,故C正确;
将图象上各点的横坐标缩短为原来的倍,得到,再将函数向左平移个单位,得到,故D错误;
故选:BC
12.CD
解:由函数的图像可知,的图像过点,
所以,可得,
因为,所以,
因为的图像过点,
所以,解得,
所以,
因为,所以不妨设,则可得,
所以,
因为,
所以,
因为对于任意的,
所以,
所以,
所以,
当时,,
当时,,
故选:CD
13.
将函数的图象向右平移个单位,
得到,
因为,
所以,,即,.
又因为,所以.
故答案为:
14.
解:将图像上所有点的横坐标缩短为原来的(纵坐标保持不变),得到,再将的图像向右平移个单位长度得到.
故答案为:
15.
由题意可得,可得,则,所以
则
由,所以
则,所以
所以
故答案为:
16.②④
将函数的图象向左平移个单位长度,得到的图象,
所以.
函数的定义域为,,
所以函数为偶函数,所以①正确;
,,
所以当时,,所以当时,与的图象有无数个交点,所以方程在区间上有无数个实根,所以②不正确;
因为,
作出函数的部分图象如图所示,
所以函数的单调递减区间为和,所以③正确;
函数的值域与的值域相同,均为,所以④不正确.
故答案为:②④.
17.(1)见解析(2) 见解析(3) .
解:(1)先列表,后描点并画图
0
x
y 0 1 0 -1 0
;
(2)把的图象上所有的点向左平移个单位, 再把所得图象的点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象,即的图象;
(3)由,
所以函数的对称轴方程是.
18.(1),对称中心的坐标为,;(2)时,取得最小值;时,取得最大值.
解:(1)由图象可知,可得:,,
又由于,可得:,所以,
由图象及五点法作图可知:,所以,
所以.
令,,得,,
所以的对称中心的坐标为,.
(2)将的图象向左平移个单位,得到;
再将横坐标伸长到原来的2倍,纵坐标不变,得到;
将图象向上平移1个单位,得到,
即,
因为,所以,
所以当,即时,取得最小值,
当,即时,取得最大值.
19.
(1),
(2)
(1)
选条件①:(1)∵的最小正周期为,
∴,∴.又是偶函数,∴对恒成立,∴对恒成立,
∴,∴.又,∴.
选条件②:∵函数图象上相邻两个最高点之间的距离为,
∴,∴.
又,∴,即,
∴,
又,∴.
选条件③:∵直线与直线是图象上相邻的两条对称轴,
∴,即,∴.
又.∴,∴,又,∴.
(2)
由(1)无论选择①②③均有,,,
将的图象向右平移个单位长度后,得到的图象,
将的图象上所有点的横坐标伸长为原来的4倍,
纵坐标不变,得到的图象.
由,
得,
∵,∴,
∴在上的单调递减区间是.
20.
(1),
(2)
解:(1)
由题意可知,,
不妨设最小正周期为,
由图像知,,即,则,
∵点在的图象上,
∴,,即,.
∵,∴,
故,.
(2)
在中,令,则,故点坐标为,
将代入,解得,,
从而曲线OD的方程为:,
当时,则,故点坐标为,
∴矩形PMFE的面积为,
即儿童乐园的面积为.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
