5.6.1函数y=Asin(ωx+φ)的图象(1) 课件—2020-2021学年人教版(2019)高中数学必修第一册(共33张PPT)
文档属性
| 名称 | 5.6.1函数y=Asin(ωx+φ)的图象(1) 课件—2020-2021学年人教版(2019)高中数学必修第一册(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 648.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 16:02:37 | ||
图片预览





文档简介
(共33张PPT)
函数
y=Asin( x+ )的图象
在物理和工程技术的许多问题中,都要遇到形如y=Asin(ωx+φ)的函数解析式(其中A,ω,φ是常数)如交流电、振动和波等.
引 言
-
-
-1
1
-
-1
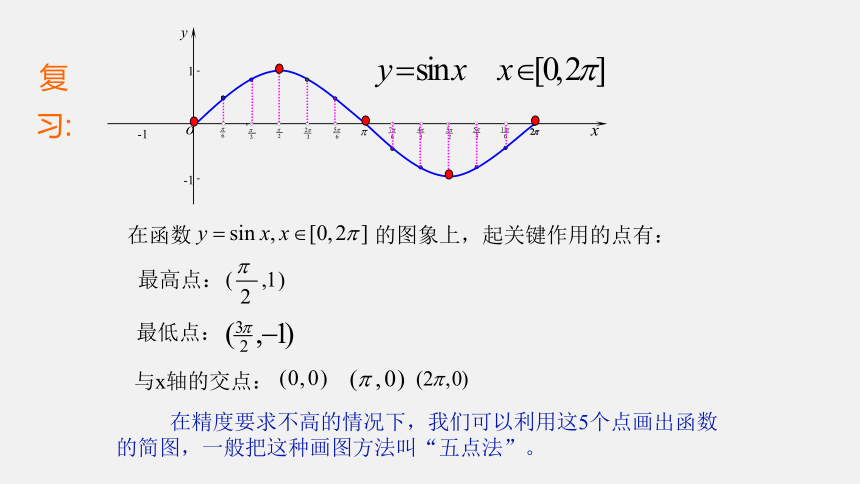
在函数 的图象上,起关键作用的点有:
最高点:
最低点:
与x轴的交点:
在精度要求不高的情况下,我们可以利用这5个点画出函数
的简图,一般把这种画图方法叫“五点法”。
复习:
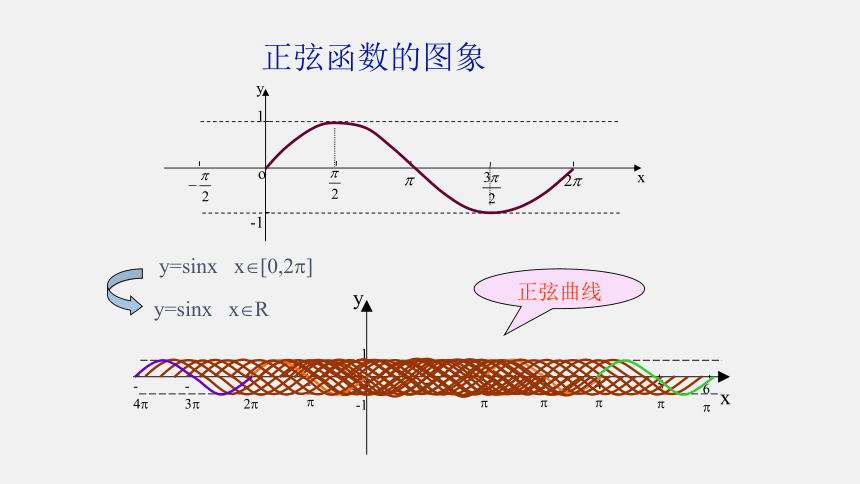
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=sinx x [0,2 ]
y=sinx x R
正弦曲线
y
x
o
1
-1
x
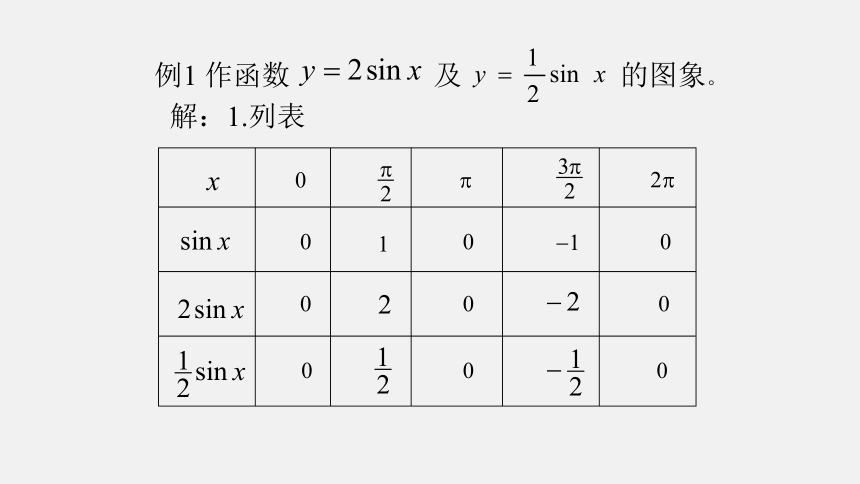
例1 作函数 及 的图象。
解:1.列表
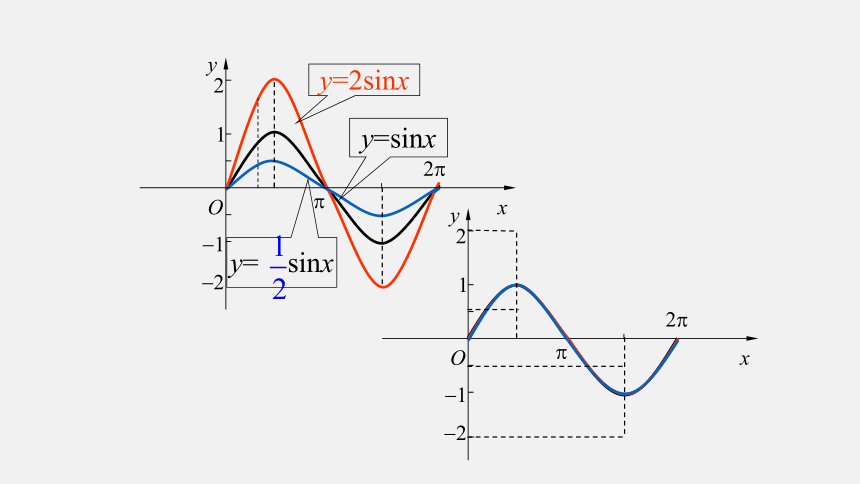
y=2sinx
y=sinx
y= sinx
x
y
O
2
1
2
2
1
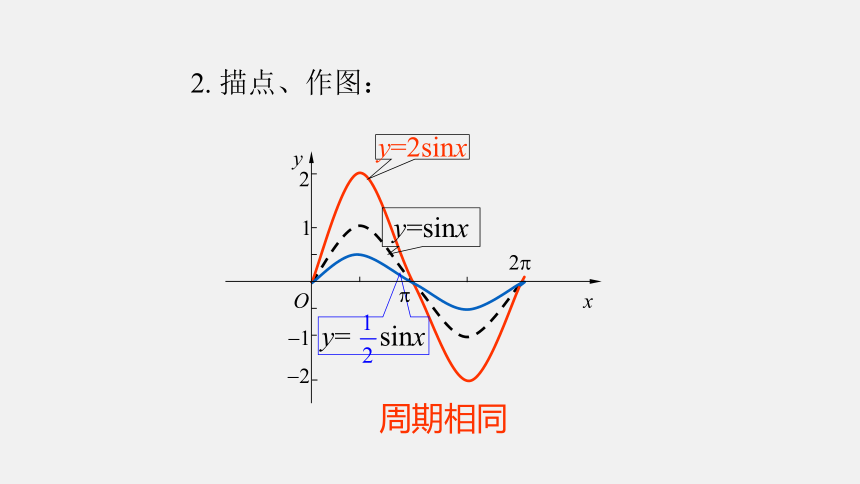
2. 描点、作图:
周期相同
x
y
O
2
1
2
2
1
x
y
O
2
1
2
2
1
y=2sinx
y=sinx
y= sinx
x
y
O
2
1
2
2
1
y= sinx
y=2sinx
y=2sinx的图象可以看作是把 y=sinx的图象上所有点的纵坐标伸长到原来的2倍。
y= sinx的图象可以看作是把 y=sinx的图象上所有点的纵坐标缩短到原来的 倍。
x
y
O
2
1
2
2
1
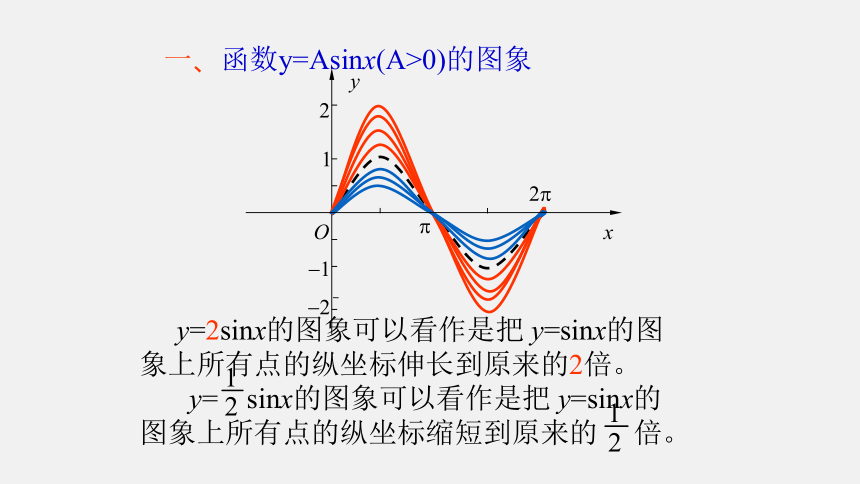
一、函数y=Asinx(A>0)的图象
函数y=Asinx (A >0且A≠1)的图象可以看作是把 y=sinx 的图象上所有点的纵坐标伸长 (当A>1时)或缩短(当0练习:作下列函数在长度为一个周期的闭区间上的简图:
结论一
1. 列表:
x
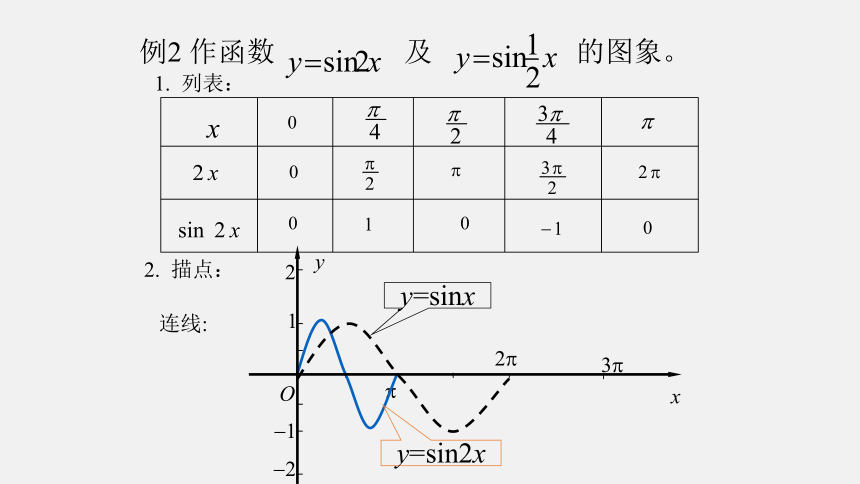
例2 作函数 及 的图象。
x
O
y
2
1
2
2
1
3
2. 描点:
y=sin2x
y=sinx
连线:
1. 列表:
x
y
O
2
1
1
3
4
2. 描点 作图:
y=sin x
y=sinx
x
y
O
2
1
1
3
4
x
y
O
2
1
1
3
4
y=sin x
y=sin2x
y=sinx
振幅相同
x
y
O
2
1
1
3
4
y=sin x的图象可以看作是把 y=sinx的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)。
y=sin 2x的图象可以看作是把 y=sinx的图象上所有点的横坐标缩短到原来的 倍(纵坐标不变)。
二、函数y=sin x( >0)图象
y=sin x
y=sin2x
y=sinx
函数y=sin x ( >0且 ≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时) 到原来的 倍(纵坐标不变) 而得到的。
练习:作下列函数在长度为一个周期的闭区间上的简图:
结论二
x
1
1
O
2
3
4
伸长为原来的2倍
图象上各点横坐标
缩短为原来的一半
图象上各点纵坐标
法一:
x
y
O
2
1
1
3
4
伸长为原来的2倍
图象上各点横坐标
缩短为原来的一半
图象上各点纵坐标
法二:
例3 作函数 及 的图象。
x
0
1
0
-1
0
y
x
O
2
1
1
作图
x
O
2
1
1
x
O
2
1
1
三、函数y=sin(x+φ)图象
x
O
2
1
1
三、函数y=sin(x+φ)图象
函数y=sin(x+φ) 的图象可以看作是把 y=sinx 的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位而得到的。
结论三
例4 作函数 及 的图象。
x
0
1
0
-1
0
y
x
O
1
1
作图
y=sin2x
四、函数y=sin(ωx+φ)与y=sinωx图象的关系
y
x
O
1
1
周期相同
想一想
它们的周期有何关系
y
x
O
1
1
函数y=sin(ωx+φ) 的图象可以看作是把 y=sinωx 的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移| |个单位而得到的。
结论四
巩固练习:
1、怎样由函数 的图象得到函数
的图象?
2、怎样由函数 的图象得到函数
的图象?
3、怎样由函数 的图象得到函数
的图象?
所有点的横坐标
伸长为原来的多少倍?
所有的点向那边
平移多少个单位?
所有点的纵坐标
伸长为原来的多少倍?
例5 作函数 及 的图象。
x
O
2
1
1
作图
函数y=sin( x +φ) ( >0且 ≠1)的图象可以
看作是把 y=sin(x +φ) 的图象上所有点的横坐标
缩短(当 >1时)或伸长(当0< <1时) 到原来的
倍(纵坐标不变) 而得到的。
结论五
所有点的横坐标
伸长为原来的2倍
所有的点向右
平移多少个单位?
所有点的纵坐标
伸长为原来的2倍
所有的点向右
平移多少个单位?
所有点的纵坐标
伸长为原来的多少倍?
所有点的横坐标
伸长为原来的多少倍?
途径一:
途径二:
y=sinx
y=sin(x+ )
横坐标缩短 >1 (伸长0< <1)到原来的1/ 倍
y=sin( x+ )
纵坐标伸长A>1 (缩短0y=Asin( x+ )
y=sinx
y=Asin( x+ )
总结:
向左 >0 (向右 <0)
方法1:(按 顺序变换)
平移| |个单位
纵坐标不变
横坐标不变
y=sinx
横坐标缩短 >1 (伸长0< <1)到原来的1/ 倍
y=sin x
纵坐标伸长A>1 (缩短0y=Asin( x+ )
y=sinx
y=Asin( x+ )
总结:
纵坐标不变
横坐标不变
方法2:(按 顺序变换)
向左 >0 (向右 <0)
平移| |/ 个单位
作业:
作业本119页1-11,,12选做。
最后一张:学习评估与反思
等第 要求(根据学习结果填写)
1 A优秀
2 B良好
3 C一般
4 D合格
目的:提升课堂教学效率,促进学生反思。
函数
y=Asin( x+ )的图象
在物理和工程技术的许多问题中,都要遇到形如y=Asin(ωx+φ)的函数解析式(其中A,ω,φ是常数)如交流电、振动和波等.
引 言
-
-
-1
1
-
-1
在函数 的图象上,起关键作用的点有:
最高点:
最低点:
与x轴的交点:
在精度要求不高的情况下,我们可以利用这5个点画出函数
的简图,一般把这种画图方法叫“五点法”。
复习:
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=sinx x [0,2 ]
y=sinx x R
正弦曲线
y
x
o
1
-1
x
例1 作函数 及 的图象。
解:1.列表
y=2sinx
y=sinx
y= sinx
x
y
O
2
1
2
2
1
2. 描点、作图:
周期相同
x
y
O
2
1
2
2
1
x
y
O
2
1
2
2
1
y=2sinx
y=sinx
y= sinx
x
y
O
2
1
2
2
1
y= sinx
y=2sinx
y=2sinx的图象可以看作是把 y=sinx的图象上所有点的纵坐标伸长到原来的2倍。
y= sinx的图象可以看作是把 y=sinx的图象上所有点的纵坐标缩短到原来的 倍。
x
y
O
2
1
2
2
1
一、函数y=Asinx(A>0)的图象
函数y=Asinx (A >0且A≠1)的图象可以看作是把 y=sinx 的图象上所有点的纵坐标伸长 (当A>1时)或缩短(当0
结论一
1. 列表:
x
例2 作函数 及 的图象。
x
O
y
2
1
2
2
1
3
2. 描点:
y=sin2x
y=sinx
连线:
1. 列表:
x
y
O
2
1
1
3
4
2. 描点 作图:
y=sin x
y=sinx
x
y
O
2
1
1
3
4
x
y
O
2
1
1
3
4
y=sin x
y=sin2x
y=sinx
振幅相同
x
y
O
2
1
1
3
4
y=sin x的图象可以看作是把 y=sinx的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)。
y=sin 2x的图象可以看作是把 y=sinx的图象上所有点的横坐标缩短到原来的 倍(纵坐标不变)。
二、函数y=sin x( >0)图象
y=sin x
y=sin2x
y=sinx
函数y=sin x ( >0且 ≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时) 到原来的 倍(纵坐标不变) 而得到的。
练习:作下列函数在长度为一个周期的闭区间上的简图:
结论二
x
1
1
O
2
3
4
伸长为原来的2倍
图象上各点横坐标
缩短为原来的一半
图象上各点纵坐标
法一:
x
y
O
2
1
1
3
4
伸长为原来的2倍
图象上各点横坐标
缩短为原来的一半
图象上各点纵坐标
法二:
例3 作函数 及 的图象。
x
0
1
0
-1
0
y
x
O
2
1
1
作图
x
O
2
1
1
x
O
2
1
1
三、函数y=sin(x+φ)图象
x
O
2
1
1
三、函数y=sin(x+φ)图象
函数y=sin(x+φ) 的图象可以看作是把 y=sinx 的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位而得到的。
结论三
例4 作函数 及 的图象。
x
0
1
0
-1
0
y
x
O
1
1
作图
y=sin2x
四、函数y=sin(ωx+φ)与y=sinωx图象的关系
y
x
O
1
1
周期相同
想一想
它们的周期有何关系
y
x
O
1
1
函数y=sin(ωx+φ) 的图象可以看作是把 y=sinωx 的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移| |个单位而得到的。
结论四
巩固练习:
1、怎样由函数 的图象得到函数
的图象?
2、怎样由函数 的图象得到函数
的图象?
3、怎样由函数 的图象得到函数
的图象?
所有点的横坐标
伸长为原来的多少倍?
所有的点向那边
平移多少个单位?
所有点的纵坐标
伸长为原来的多少倍?
例5 作函数 及 的图象。
x
O
2
1
1
作图
函数y=sin( x +φ) ( >0且 ≠1)的图象可以
看作是把 y=sin(x +φ) 的图象上所有点的横坐标
缩短(当 >1时)或伸长(当0< <1时) 到原来的
倍(纵坐标不变) 而得到的。
结论五
所有点的横坐标
伸长为原来的2倍
所有的点向右
平移多少个单位?
所有点的纵坐标
伸长为原来的2倍
所有的点向右
平移多少个单位?
所有点的纵坐标
伸长为原来的多少倍?
所有点的横坐标
伸长为原来的多少倍?
途径一:
途径二:
y=sinx
y=sin(x+ )
横坐标缩短 >1 (伸长0< <1)到原来的1/ 倍
y=sin( x+ )
纵坐标伸长A>1 (缩短0
y=sinx
y=Asin( x+ )
总结:
向左 >0 (向右 <0)
方法1:(按 顺序变换)
平移| |个单位
纵坐标不变
横坐标不变
y=sinx
横坐标缩短 >1 (伸长0< <1)到原来的1/ 倍
y=sin x
纵坐标伸长A>1 (缩短0
y=sinx
y=Asin( x+ )
总结:
纵坐标不变
横坐标不变
方法2:(按 顺序变换)
向左 >0 (向右 <0)
平移| |/ 个单位
作业:
作业本119页1-11,,12选做。
最后一张:学习评估与反思
等第 要求(根据学习结果填写)
1 A优秀
2 B良好
3 C一般
4 D合格
目的:提升课堂教学效率,促进学生反思。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
