人教版数学八上12.2三角形全等的判定(4)课时练习(word版、含答案)
文档属性
| 名称 | 人教版数学八上12.2三角形全等的判定(4)课时练习(word版、含答案) | 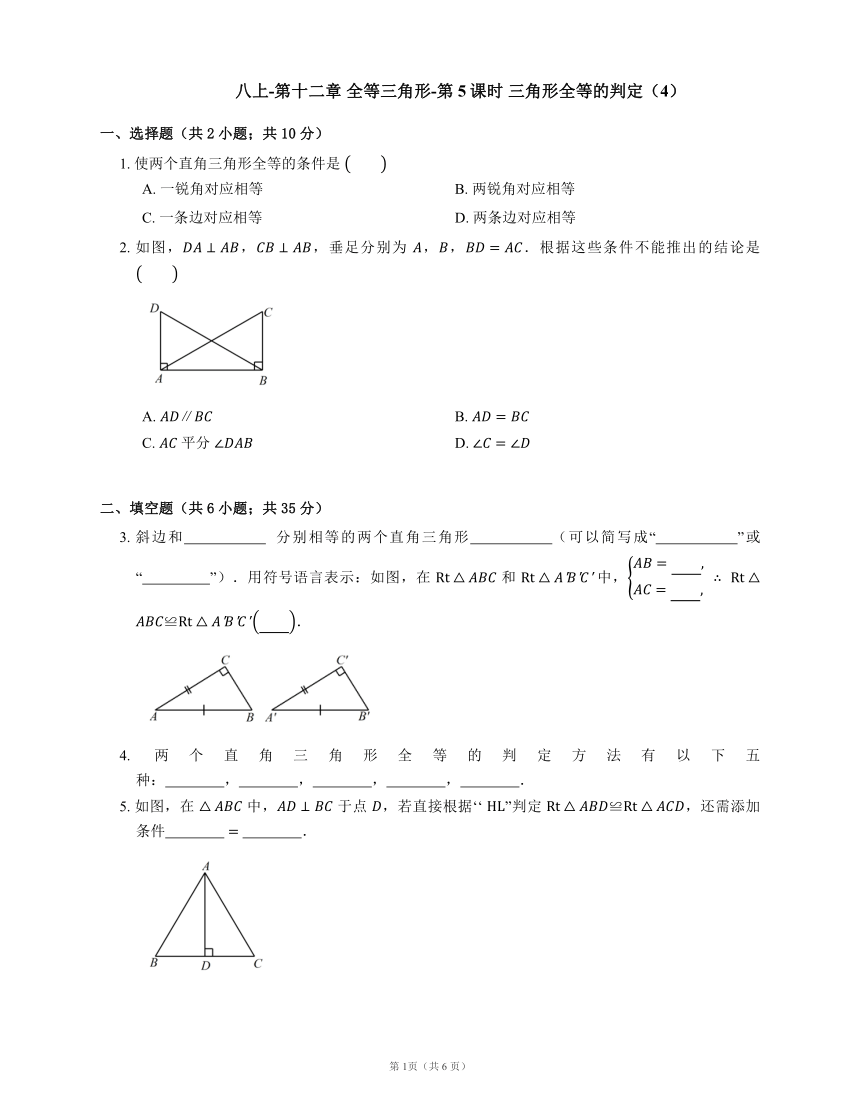 | |
| 格式 | docx | ||
| 文件大小 | 312.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 15:42:51 | ||
图片预览

文档简介
八上-第十二章 全等三角形-第5课时 三角形全等的判定(4)
一、选择题(共2小题;共10分)
1. 使两个直角三角形全等的条件是
A. 一锐角对应相等 B. 两锐角对应相等
C. 一条边对应相等 D. 两条边对应相等
2. 如图,,,垂足分别为 ,,.根据这些条件不能推出的结论是
A. B.
C. 平分 D.
二、填空题(共6小题;共35分)
3. 斜边和 分别相等的两个直角三角形 (可以简写成“ ”或“ ”).用符号语言表示:如图,在 和 中, .
4. 两个直角三角形全等的判定方法有以下五种: , , , , .
5. 如图,在 中, 于点 ,若直接根据‘‘ ”判定 ,还需添加条件 .
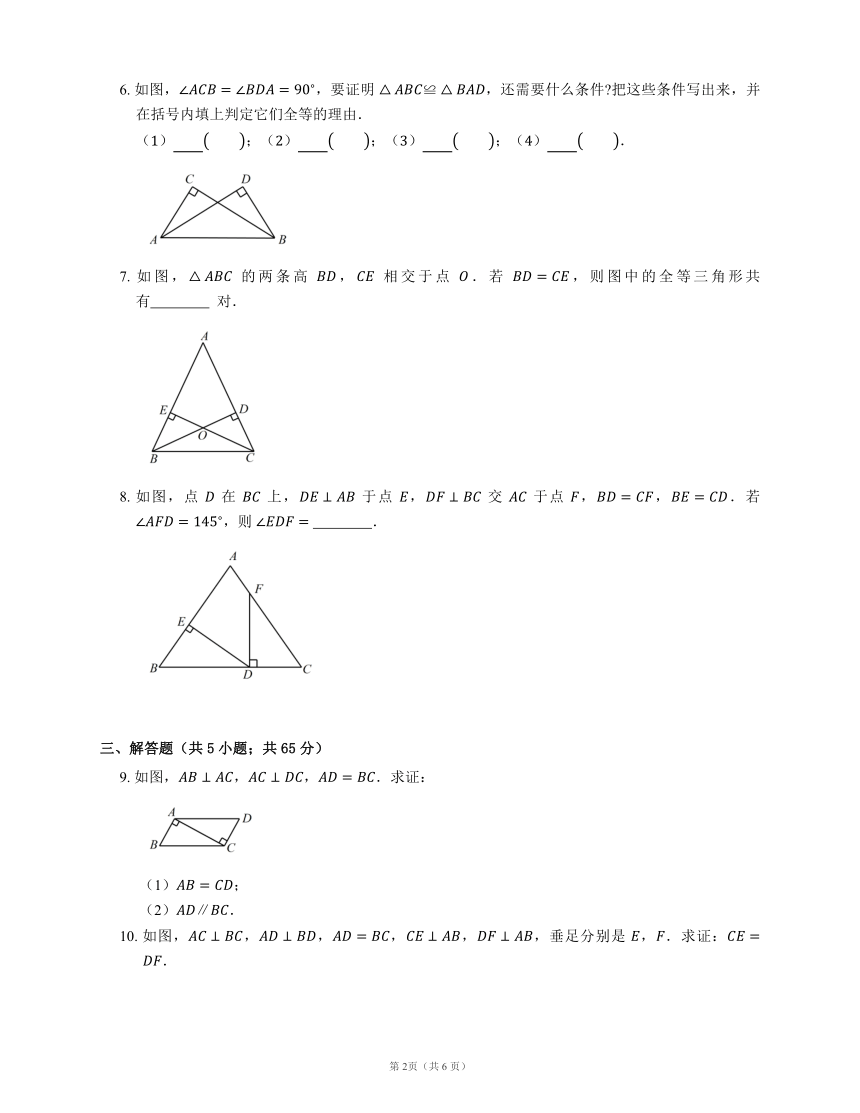
6. 如图,,要证明 ,还需要什么条件 把这些条件写出来,并在括号内填上判定它们全等的理由.
();();();().
7. 如图, 的两条高 , 相交于点 .若 ,则图中的全等三角形共有 对.
8. 如图,点 在 上, 于点 , 交 于点 ,,.若 ,则 .
三、解答题(共5小题;共65分)
9. 如图,,,.求证:
(1);
(2).
10. 如图,,,,,,垂足分别是 ,.求证:.
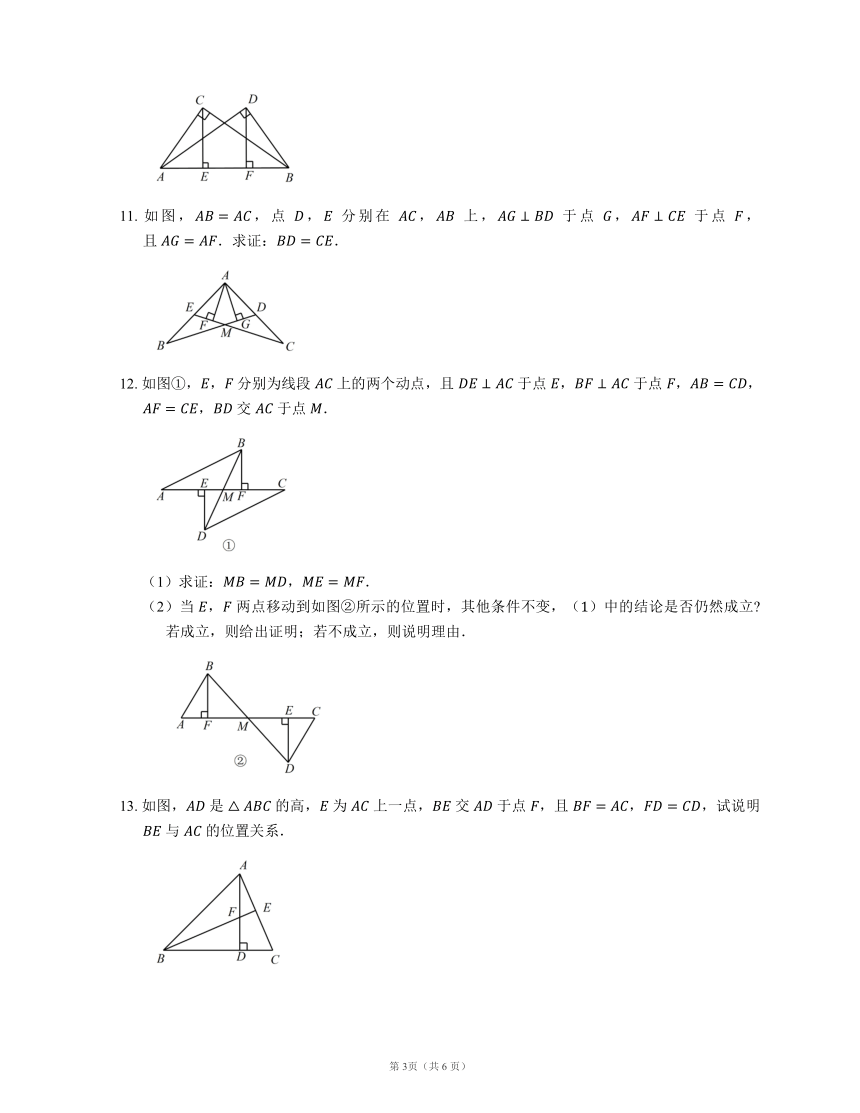
11. 如图,,点 , 分别在 , 上, 于点 , 于点 ,且 .求证:.
12. 如图①,, 分别为线段 上的两个动点,且 于点 , 于点 ,,, 交 于点 .
(1)求证:,.
(2)当 , 两点移动到如图②所示的位置时,其他条件不变,()中的结论是否仍然成立 若成立,则给出证明;若不成立,则说明理由.
13. 如图, 是 的高, 为 上一点, 交 于点 ,且 ,,试说明 与 的位置关系.
答案
第一部分
1. D
2. C
第二部分
3. 一条直角边,全等,斜边、直角边,,,,
4. ,,,,
5. ,
6. ,,,,,,,
7.
8.
第三部分
9. (1) 因为 ,,
所以 .
在 和 中,
所以 .
所以 .
(2) 由()知 ,
所以 .
所以 .
10. ,,
.
在 和 中,
.
,,即 .
,,
.
在 和 中,
.
.
11. ,,
.
在 和 中,
.
.
在 和 中,
.
.
12. (1) ,,
.
在 和 中,
.
.
在 和 中,
.
,.
(2) ()中的结论仍然成立.
,,
.
在 和 中,
.
.
在 和 中,
.
,.
13. 是 的高,
.
在 和 中,
.
.
,
.
.
.
第1页(共1 页)
一、选择题(共2小题;共10分)
1. 使两个直角三角形全等的条件是
A. 一锐角对应相等 B. 两锐角对应相等
C. 一条边对应相等 D. 两条边对应相等
2. 如图,,,垂足分别为 ,,.根据这些条件不能推出的结论是
A. B.
C. 平分 D.
二、填空题(共6小题;共35分)
3. 斜边和 分别相等的两个直角三角形 (可以简写成“ ”或“ ”).用符号语言表示:如图,在 和 中, .
4. 两个直角三角形全等的判定方法有以下五种: , , , , .
5. 如图,在 中, 于点 ,若直接根据‘‘ ”判定 ,还需添加条件 .
6. 如图,,要证明 ,还需要什么条件 把这些条件写出来,并在括号内填上判定它们全等的理由.
();();();().
7. 如图, 的两条高 , 相交于点 .若 ,则图中的全等三角形共有 对.
8. 如图,点 在 上, 于点 , 交 于点 ,,.若 ,则 .
三、解答题(共5小题;共65分)
9. 如图,,,.求证:
(1);
(2).
10. 如图,,,,,,垂足分别是 ,.求证:.
11. 如图,,点 , 分别在 , 上, 于点 , 于点 ,且 .求证:.
12. 如图①,, 分别为线段 上的两个动点,且 于点 , 于点 ,,, 交 于点 .
(1)求证:,.
(2)当 , 两点移动到如图②所示的位置时,其他条件不变,()中的结论是否仍然成立 若成立,则给出证明;若不成立,则说明理由.
13. 如图, 是 的高, 为 上一点, 交 于点 ,且 ,,试说明 与 的位置关系.
答案
第一部分
1. D
2. C
第二部分
3. 一条直角边,全等,斜边、直角边,,,,
4. ,,,,
5. ,
6. ,,,,,,,
7.
8.
第三部分
9. (1) 因为 ,,
所以 .
在 和 中,
所以 .
所以 .
(2) 由()知 ,
所以 .
所以 .
10. ,,
.
在 和 中,
.
,,即 .
,,
.
在 和 中,
.
.
11. ,,
.
在 和 中,
.
.
在 和 中,
.
.
12. (1) ,,
.
在 和 中,
.
.
在 和 中,
.
,.
(2) ()中的结论仍然成立.
,,
.
在 和 中,
.
.
在 和 中,
.
,.
13. 是 的高,
.
在 和 中,
.
.
,
.
.
.
第1页(共1 页)
