2021-2022学年人教版数学九年级上册24.1.2 垂直于弦的直径 课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.1.2 垂直于弦的直径 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 423.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 15:22:18 | ||
图片预览






文档简介
(共19张PPT)
垂直于弦的直径
目录
01
教学目标
02
知识点框架
03
例题练习
04
作业布置
教学目标
01
教学目标
理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.
灵活运用垂径定理解决有关圆的问题.
知识点框架
02
知识点框架
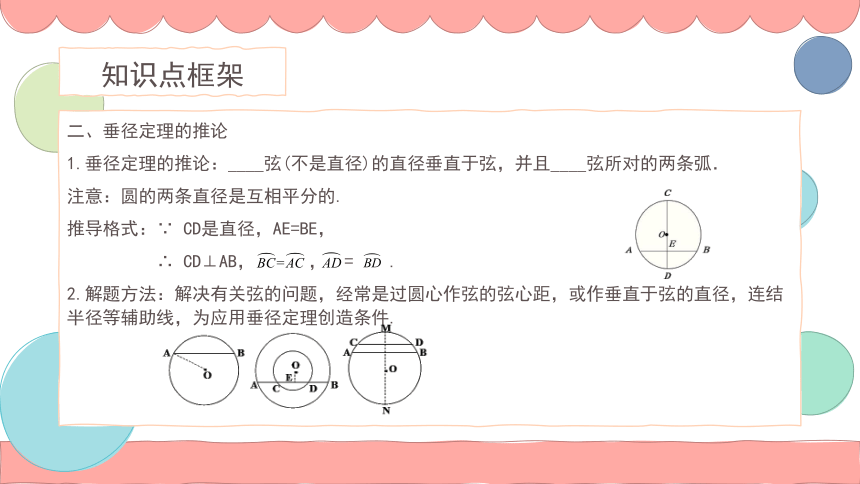
二、垂径定理的推论
1.垂径定理的推论:____弦(不是直径)的直径垂直于弦,并且____弦所对的两条弧.
注意:圆的两条直径是互相平分的.
推导格式:∵ CD是直径,AE=BE,
∴ CD⊥AB, , = .
2.解题方法:解决有关弦的问题,经常是过圆心作弦的弦心距,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件.
例题练习
03
例题
例.已知:⊙O中弦AB∥CD,求证: = .
例4.(多解)已知⊙O的半径为13,弦AB=24,弦CD=10,AB∥CD,求这两条平行弦AB、CD之间的距离.
练习
1.如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦AB的长是多少?
2.一条排水管的截面如图所示.已知排水管的半径OB=10 cm,水面宽AB=16 cm.求截面圆心O到水面的距离.
练习
3.有一石拱桥的桥拱是圆弧形,如图所示,正常水位下水面宽AB=60 m,水面到拱顶距离CD=18 m,当洪水泛滥时,水面到拱顶距离为3.5 m时需要采取紧急措施,当水面宽MN=32 m时是否需要采取紧急措施?请说明理由.
4.(多解)已知⊙O的半径为10cm,弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为 .
小结
作业布置
04
作业布置
8. 如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m.求这段弯路的半径.
9. 如图,点A、B是⊙O上两点,AB=10cm,点P是⊙O上的动点(与A、B不重合),连接AP、BP,过点O分别作OE⊥AP于E,OF⊥PB于F,求EF的长.
下节课见!
垂直于弦的直径
目录
01
教学目标
02
知识点框架
03
例题练习
04
作业布置
教学目标
01
教学目标
理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.
灵活运用垂径定理解决有关圆的问题.
知识点框架
02
知识点框架
二、垂径定理的推论
1.垂径定理的推论:____弦(不是直径)的直径垂直于弦,并且____弦所对的两条弧.
注意:圆的两条直径是互相平分的.
推导格式:∵ CD是直径,AE=BE,
∴ CD⊥AB, , = .
2.解题方法:解决有关弦的问题,经常是过圆心作弦的弦心距,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件.
例题练习
03
例题
例.已知:⊙O中弦AB∥CD,求证: = .
例4.(多解)已知⊙O的半径为13,弦AB=24,弦CD=10,AB∥CD,求这两条平行弦AB、CD之间的距离.
练习
1.如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦AB的长是多少?
2.一条排水管的截面如图所示.已知排水管的半径OB=10 cm,水面宽AB=16 cm.求截面圆心O到水面的距离.
练习
3.有一石拱桥的桥拱是圆弧形,如图所示,正常水位下水面宽AB=60 m,水面到拱顶距离CD=18 m,当洪水泛滥时,水面到拱顶距离为3.5 m时需要采取紧急措施,当水面宽MN=32 m时是否需要采取紧急措施?请说明理由.
4.(多解)已知⊙O的半径为10cm,弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为 .
小结
作业布置
04
作业布置
8. 如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m.求这段弯路的半径.
9. 如图,点A、B是⊙O上两点,AB=10cm,点P是⊙O上的动点(与A、B不重合),连接AP、BP,过点O分别作OE⊥AP于E,OF⊥PB于F,求EF的长.
下节课见!
同课章节目录
