2021--2022学年人教版九年级数学上册24.1.3弧、弦、圆心角 课件(共20张PPT)
文档属性
| 名称 | 2021--2022学年人教版九年级数学上册24.1.3弧、弦、圆心角 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 345.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
弧、弦、圆心角
目录
01
教学目标
02
知识点框架
03
例题练习
04
作业布置
教学目标
01
教学目标
理解圆心角的概念,掌握圆的中心对称性和旋转不变性.
理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.
知识点框架
02
知识点框架
1.圆心角:顶点在圆心的角,叫________,如∠AOB .
圆心角 ∠AOB所对的弧为 ;
圆心角 ∠AOB所对的弦为AB.
2.圆的性质:
圆是中心对称图形,____就是它的对称中心;把圆绕圆心旋转一个角度,所得的图形与原图形____.
圆是轴对称图形,对称轴为经过________所在的直线。
知识点框架
3.弧、弦与圆心角的关系定理:
在同一个圆中(或等圆),如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
在同一个圆中(或等圆),如果弧相等,那么它们所对的圆心角相等,所对的弦相等.
在同一个圆中(或等圆),如果弦相等,那么它们所对的圆心角相等,所对的弧相等.
例题练习
03
例题
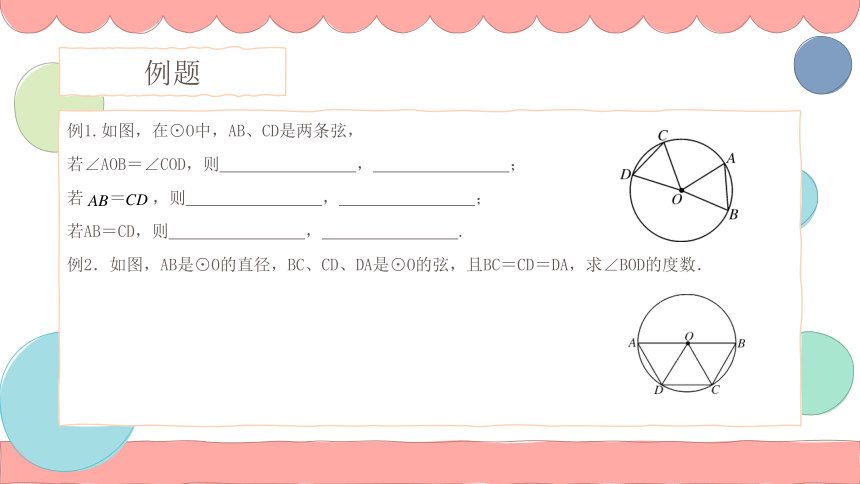
例1.如图,在⊙O中,AB、CD是两条弦,
若∠AOB=∠COD,则 , ;
若 = ,则 , ;
若AB=CD,则 , .
例2.如图,AB是⊙O的直径,BC、CD、DA是⊙O的弦,且BC=CD=DA,求∠BOD的度数.
例题
例3.如图,已知AB是⊙O的直径,M、N分别是AO、BO的中点,CM⊥AB,DN⊥AB.
求证: =
练习
1.如图所示,A、B、C是⊙O上三点,∠AOB=120°,C是 的中点,试判断四边形OACB的形状,并说明理由.
练习
2.如图,在⊙O中,弦AB=CD,那么∠AOC和∠BOD相等吗?请说明理由.
练习
3.如图,⊙O中,已知∠AOB=2∠COD,求证:2CD>AB.
小结
总结:1.在同圆或等圆中,两个圆心角、两条弧、两条弦这三组量中有一组量相等,其余的两组量也相等,简称“知一推二”,在已知两个圆心角相等或由两弦推两个圆心角相等时,必须限定同圆或等圆;2.求一个角的度数可先根据弧、弦、圆心角的关系得出所求角与已知角之间的等量关系,然后结合对顶角、等腰三角形或三角形内角和等性质求解。
作业布置
04
作业布置
1.如图,在⊙O中,已知 = ,则AC与BD的关系是( )
A.AC=BD B.AC<BD
C.AC>BD D.不确定
2.如图所示,MN为 ⊙O的弦,∠MON=70°,则∠N的度数为( )
A. 40°
B. 50°
C. 55°
D. 60°
作业布置
3.弦长等于半径的弦所对的圆心角等于 .
4.半径为R的⊙O中,弦AB=2R,弦CD=R,若两弦的弦心距分别为OE、OF,则OE∶OF等于 .
5.如图,同心圆中,大圆的弦AB交小圆于C、D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为 .
作业布置
6.如图,已知AB、CD是⊙O的直径,E是⊙O上一点,且 .
求证:BD=DE.
7.如图,已知AB,CD是⊙O的直径,CE是弦,且AB∥CE,∠C=35°,则 的度数为多少?
作业布置
8.如图,AB是半圆O的直径,C、D是半径OA、OB的中点且OA⊥CE、OB⊥DE,
求证:
9.如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,作AD,BC于E,F,延长BA交⊙O于G,求证: .
下节课见!
弧、弦、圆心角
目录
01
教学目标
02
知识点框架
03
例题练习
04
作业布置
教学目标
01
教学目标
理解圆心角的概念,掌握圆的中心对称性和旋转不变性.
理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.
知识点框架
02
知识点框架
1.圆心角:顶点在圆心的角,叫________,如∠AOB .
圆心角 ∠AOB所对的弧为 ;
圆心角 ∠AOB所对的弦为AB.
2.圆的性质:
圆是中心对称图形,____就是它的对称中心;把圆绕圆心旋转一个角度,所得的图形与原图形____.
圆是轴对称图形,对称轴为经过________所在的直线。
知识点框架
3.弧、弦与圆心角的关系定理:
在同一个圆中(或等圆),如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
在同一个圆中(或等圆),如果弧相等,那么它们所对的圆心角相等,所对的弦相等.
在同一个圆中(或等圆),如果弦相等,那么它们所对的圆心角相等,所对的弧相等.
例题练习
03
例题
例1.如图,在⊙O中,AB、CD是两条弦,
若∠AOB=∠COD,则 , ;
若 = ,则 , ;
若AB=CD,则 , .
例2.如图,AB是⊙O的直径,BC、CD、DA是⊙O的弦,且BC=CD=DA,求∠BOD的度数.
例题
例3.如图,已知AB是⊙O的直径,M、N分别是AO、BO的中点,CM⊥AB,DN⊥AB.
求证: =
练习
1.如图所示,A、B、C是⊙O上三点,∠AOB=120°,C是 的中点,试判断四边形OACB的形状,并说明理由.
练习
2.如图,在⊙O中,弦AB=CD,那么∠AOC和∠BOD相等吗?请说明理由.
练习
3.如图,⊙O中,已知∠AOB=2∠COD,求证:2CD>AB.
小结
总结:1.在同圆或等圆中,两个圆心角、两条弧、两条弦这三组量中有一组量相等,其余的两组量也相等,简称“知一推二”,在已知两个圆心角相等或由两弦推两个圆心角相等时,必须限定同圆或等圆;2.求一个角的度数可先根据弧、弦、圆心角的关系得出所求角与已知角之间的等量关系,然后结合对顶角、等腰三角形或三角形内角和等性质求解。
作业布置
04
作业布置
1.如图,在⊙O中,已知 = ,则AC与BD的关系是( )
A.AC=BD B.AC<BD
C.AC>BD D.不确定
2.如图所示,MN为 ⊙O的弦,∠MON=70°,则∠N的度数为( )
A. 40°
B. 50°
C. 55°
D. 60°
作业布置
3.弦长等于半径的弦所对的圆心角等于 .
4.半径为R的⊙O中,弦AB=2R,弦CD=R,若两弦的弦心距分别为OE、OF,则OE∶OF等于 .
5.如图,同心圆中,大圆的弦AB交小圆于C、D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为 .
作业布置
6.如图,已知AB、CD是⊙O的直径,E是⊙O上一点,且 .
求证:BD=DE.
7.如图,已知AB,CD是⊙O的直径,CE是弦,且AB∥CE,∠C=35°,则 的度数为多少?
作业布置
8.如图,AB是半圆O的直径,C、D是半径OA、OB的中点且OA⊥CE、OB⊥DE,
求证:
9.如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,作AD,BC于E,F,延长BA交⊙O于G,求证: .
下节课见!
同课章节目录
