2021-2022学年人教版九年级数学 上册21.2.2 公式法 课件(44张)
文档属性
| 名称 | 2021-2022学年人教版九年级数学 上册21.2.2 公式法 课件(44张) |

|
|
| 格式 | zip | ||
| 文件大小 | 564.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 00:00:00 | ||
图片预览











文档简介
(共44张PPT)
人教版数学 九年级上册
第二十一章 一元二次方程
21.2 解一元二次方程
21.2.2 公式法
解:
移项,得 .
配方 .
由此可得 .
利用配方法解一元二次方程
导入新知
化:把原方程化成 x2+px+q = 0 的形式.
移项:把常数项移到方程的右边,如x2+px =-q.
配方:方程两边都加上一次项系数一半的平方.
开方:根据平方根的意义,方程两边开平方.
求解:解一元一次方程.
定解:写出原方程的解.
用配方法解一元二次方程的步骤
方程右边是非负数
x2+px+ ( )2 = -q+ ( )2
( x+ )2 =-q+ ( )2
【思考】如何用配方法解方程ax2+bx+c=0(a≠0)呢?
1.理解一元二次方程求根公式的推导过程,了解公式法的概念.
2.灵活应用 =b -4ac 的值识别一元二次方程根的情况.
3.会熟练应用公式法解一元二次方程.
学习目标
ax2+bx+c = 0(a≠0)
新知一 公式法的概念
一元二次方程的一般形式是什么?
【思考】如果使用配方法解出一元二次方程一般形式的根,那么这个根是不是可以普遍适用呢?
合作探究
用配方法解一般形式的一元二次方程
方程两边都除以a,得 ,
解:
移项,得 ,
配方,得 ,
即 .
一元二次方程的求根公式
当
, .
由上可知,一元二次方程
的根由方程的系数a,b,c确定.因此,解一元二次方程时,可以先将方程化为一般形式 ,当 时,将a,b,c 代入式子 ,就得到方程的根,这个式子叫做一元二次方程的求根公式,利用它解一元二次方程的方法叫做公式法,由求根公式可知,一元二次方程最多有两个实数根.
当 b-4ac <0 时,方程有实数根吗?
公式法的概念
解:∵a=1,b=-4,c=-7,
∴b2-4ac=(-4)2-4×1×(-7)=44>0.
例 用公式法解方程:
公式法解方程
(1)x2-4x-7=0;
∴
典例精析
解:
则方程有两个相等的实数根:
(2)2x2-2 x+1=0;
【思考】这里的a、b、c的值分别是什么?
解:原方程可化为 .
则方程有两个不相等的实数根
(3)5x2-3x=x+1;
.
.
解:原方程可化为 .
方程无实数根.
(4)x2+17=8x.
.
(1)当
时,一元二次方程有两个不
相等的实数根;
(2)当
时,一元二次方程有两个相
等的实数根;
(3)当
时,一元二次方程没有实
数根.
方法点拨
用公式法解一元二次方程的一般步骤
1. 将方程化成一般形式,并写出a,b,c 的值.
2. 求出 的值.
3. (1)当 >0 时,代入求根公式 :
写出一元二次方程的根.
(2)当 =0时,代入求根公式:
写出一元二次方程的根.
(3)当 <0时,方程无实数根.
用公式法解方程:
解:a=3, b=-6, c=-2,
=b2-4ac=(-6)2-4×3×(-2)=60.
巩固练习
用公式法解下列方程:
(1) x2+x-1 = 0 (2)x2-2
(3) 2x2-2x+1 = 0
x+3 = 0
观察上面解一元二次方程的过程,一元二次方程的根的情况与一元二次方程中二次项系数、一次项系数及常数项有关吗?能否根据这个关系不解方程得出方程的解的情况呢?
新知二 一元二次方程的根的情况
合作探究
【思考】
不解方程,你能判断下列方程根的情况吗?
⑴ x2+2x-8 = 0
⑵ x2 = 4x-4
⑶ x2-3x = -3
(3)没有实数根.
答案:(1)有两个不相等的实数根;
(2)有两个相等的实数根;
【发现】b2-4ac的符号决定着方程的解.
(2)当b2-4ac=0时,有两个相等的实数根:
(1)当b2-4ac>0 时,有两个不等的实数根:
(3)当b2-4ac<0时,没有实数根.
一般的,式子 b2-4ac 叫做一元二次方程根的判别式,通常用希腊字母“ ”来表示,即 =b2-4ac.
一元二次方程的根的情况
若已知一个一元二次方程的根的情况,是否能得到判别式的值的符号呢?
当一元二次方程有两个不相等的实数根时, b2-4ac >0;
当一元二次方程有两个相等的实数根时, b2-4ac = 0;
当一元二次方程没有实数根时, b2-4ac < 0.
【注意】
一元二次方程的根的情况
例1 不解方程,判断下列方程根的情况:
解:a=﹣1,b= ,c=﹣6,
△= b2-4ac
=24-4×(﹣1)×(-6)=0.
该方程有两个相等的实数根.
解: 移项,得 x2+4x-2=0,
a=1,b=4 ,c=﹣2,
△= b2-4ac
=16-4×1×(-2)=24>0.
该方程有两个不相等的实数根.
利用判别式识别一元二次方程的根的情况
(2)x2+4x=2;
(1) ;
典例精析
(3)4x2+1=-3x;
解:移项,得4x2+3x+1=0,
a=4,b=3 ,c=1,
∵ △= b2-4ac
=9-4×4×1=-7<0.
∴该方程没有实数根.
解:a=1,b=-2m ,c=4(m-1),
∵ △= b2-4ac
=(-2m) -4×1×4(m-1)
=4m2-16(m-1)
=4m2-16m+16
=(2m-4)2≥0.
∴该方程有两个实数根.
(4)x -2mx+4(m-1)=0.
(2)方程ax2+bx+c=0(a≠0)有实数根,那么总成立的式
子是( )
A. b -4ac>0 B. b -4ac<0
C. b -4ac≤0 D. b -4ac≥0
(1)下列方程中,没有实数根的方程是( )
A.x =9 B.4x =3(4x-1)
C.x(x+1)=1 D.2y +6y+7=0
D
D
选一选.
巩固练习
例2 m为何值时,关于x的一元二次方程 2x2-(4m+1)x+2m2-1=0:
(1)有两个不相等的实数根?(2)有两个相等的实数根?
(3)没有实数根?
解:a=2,b=-(4m+1),c=2m2-1,
b2-4ac=〔-(4m+1)〕2-4×2(2m2-1)=8m+9.
(1)若方程有两个不相等的实数根,则b2-4ac >0,即8m+9>0 ∴m>
(2)若方程有两个相等的实数根,则b2-4ac=0即8m+9=0 ∴m=
(3)若方程没有实数根,则b2-4ac<0即8m+9<0, ∴m<
∴当m> 时,方程有两个不相等的实数根;当m= 时,
方程有两个相等的实数根;当m< 时,方程没有实数根.
利用判别式求字母的值或取值范围
典例精析
m为任意实数,试说明关于x的方程x2-(m-1)x-3(m+3)=0恒有两个不相等的实数根.
解:
∵不论m取任何实数,总有(m+5)2≥0,
∴b2-4ac=(m+5)2+12≥12>0,
∴不论m取任何实数,上述方程总有两个不相等的实数根.
巩固练习
1.方程x2-4x+4=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.有一个实数
D.没有实数根
B
课堂练习
2. 关于x的一元二次方程kx2-2x-1=0有两个不等 的实根,则k的取值范围是 ( )
A. k>-1 B. k>-1 且k≠ 0
C. k<1 D. k<1 且k≠0
B
3. 已知x2+2x=m-1没有实数根,求证:x2+mx=1-2m必有两个不相等的实数根.
证明:∵ 没有实数根,
∴ 4-4(1-m)<0, ∴m<0.
对于方程 x2+mx=1-2m ,即 .
,∵ ,∴ △>0.
∴x2+mx=1-2m必有两个不相等的实数根.
公式法
定义
把各系数直接带入求根公式的解一元二次方程的方法.
步骤
一化成一般形式, 并写出a,b,c的值;
二求出b2-4ac的值;
三;
四写出方程的解:x1, x2.
应用
用判别式△= b2-4ac判定一元二次方程根的情况.
归纳新知
1.(2020·安徽)下列方程中,有两个相等实数根的是( )
A.x2+1=2x B.x2+1=0
C.x2-2x=3 D.x2-2x=0
2.下列关于x的方程ax2-bx=0(a,b是不为0的常数)的根的情况
判断正确的是( )
A.无实数根
B.有两个不等的实数根
C.有两个相等的实数根
D.有且只有一个实数根
A
B
课后练习
3.(2020·吉林)一元二次方程x2+3x-1=0根的判别式的值为________.
4.(2020·辽阳)若关于x的一元二次方程x2+2x-k=0无实数根,
则k的取值范围是____.
k<-1
13
5.(教材P17T4变式)利用判别式判断下列方程的根的情况:
(1)9x2-6x+1=0;
解:∵a=9,b=-6,c=1,∴Δ=(-6)2-4×9×1=0,
∴此方程有两个相等的实数根
(2)8x2+4x=-3;
解:化为一般形式为8x2+4x+3=0,∵a=8,b=4,c=3,
∴Δ=42-4×8×3=-80<0,∴此方程没有实数根
(3)2(x2-1)+5x=0.
解:化为一般形式为2x2+5x-2=0,∵a=2,b=5,c=-2,
∴Δ=52-4×2×(-2)=41>0,∴此方程有两个不相等的实数根
B
A
8.一元二次方程x2-x-6=0中,b2-4ac=_____,
可得x1=________,x2=________.
25
3
-2
9.用公式法解下列方程:
(1)x2-3x-2=0;
(2)8x2-8x+1=0;
10.已知m,n是方程x2-x-1=0的两个解,若m>n,则m的值应在( )
A.0和1之间 B.1和1.5之间
C.1.5和2之间 D.2和3之间
11.(2020·潍坊)关于x的一元二次方程x2+(k-3)x+1-k=0根的情况,
下列说法正确的是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.无法确定
C
A
12.关于x 的方程(a+1)x2-4x-1=0有实数根,
则a满足的条件是_________.
13.定义:如果关于x的一元二次方程ax2+bx+c=0(a≠0)
满足a+b+c=0,那么我们称这个方程为“凤凰”方程.
已知关于x的方程x2+mx+n=0是“凤凰”方程,
且有两个相等的实数根,则mn=____.
a≥-5
-2
14.已知关于x的一元二次方程x2-3x+a-1=0有实数根.
(1)求a的取值范围;
(2)当a为符合条件的最大整数时,求此时方程的解.
15.(教材P17T13变式)已知关于x的一元二次方程(x-3)(x-2)=|m|.
(1)求证:对于任意实数m,方程总有两个不等的实数根;
(2)若方程的一个根是1,求m的值及方程的另外一个根.
解:(1)原方程整理得x2-5x+6-|m|=0,
Δ=25-4(6-|m|)=1+4|m|.∵|m|≥0, ∴Δ>0.
∴原方程有两个不相等的实数根
(2)当x=1时,将x=1代入得1-5+6-|m|=0,∴m=±2.
当m=±2时,原方程可化为x2-5x+4=0,x1=1,x2=4,
∴方程的另外一个根为4
16.已知关于x的方程x2-2(m+2)x+m2+5=0没有实数根.
(1)求m的取值范围;
(2)试判断关于x的方程(m+5)x2-2(m+1)x+m=0的根的情况.
17.已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,
其中a,b,c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
解:(1)△ABC是等腰三角形.理由:∵x=-1是方程的根,
∴(a+c)×(-1)2-2b+(a-c)=0,∴a+c-2b+a-c=0,
∴a-b=0,∴a=b,∴△ABC是等腰三角形
(2)△ABC是直角三角形.。∵方程有两个相等的实数根,
∴(2b)2-4(a+c)(a-c)=0,∴4b2-4a2+4c2=0,
∴a2=b2+c2,∴△ABC是直角三角形
(3)当a=b=c时,可整理为2ax2+2ax=0,∴x2+x=0,解得x1=0,x2=-1
再 见
人教版数学 九年级上册
第二十一章 一元二次方程
21.2 解一元二次方程
21.2.2 公式法
解:
移项,得 .
配方 .
由此可得 .
利用配方法解一元二次方程
导入新知
化:把原方程化成 x2+px+q = 0 的形式.
移项:把常数项移到方程的右边,如x2+px =-q.
配方:方程两边都加上一次项系数一半的平方.
开方:根据平方根的意义,方程两边开平方.
求解:解一元一次方程.
定解:写出原方程的解.
用配方法解一元二次方程的步骤
方程右边是非负数
x2+px+ ( )2 = -q+ ( )2
( x+ )2 =-q+ ( )2
【思考】如何用配方法解方程ax2+bx+c=0(a≠0)呢?
1.理解一元二次方程求根公式的推导过程,了解公式法的概念.
2.灵活应用 =b -4ac 的值识别一元二次方程根的情况.
3.会熟练应用公式法解一元二次方程.
学习目标
ax2+bx+c = 0(a≠0)
新知一 公式法的概念
一元二次方程的一般形式是什么?
【思考】如果使用配方法解出一元二次方程一般形式的根,那么这个根是不是可以普遍适用呢?
合作探究
用配方法解一般形式的一元二次方程
方程两边都除以a,得 ,
解:
移项,得 ,
配方,得 ,
即 .
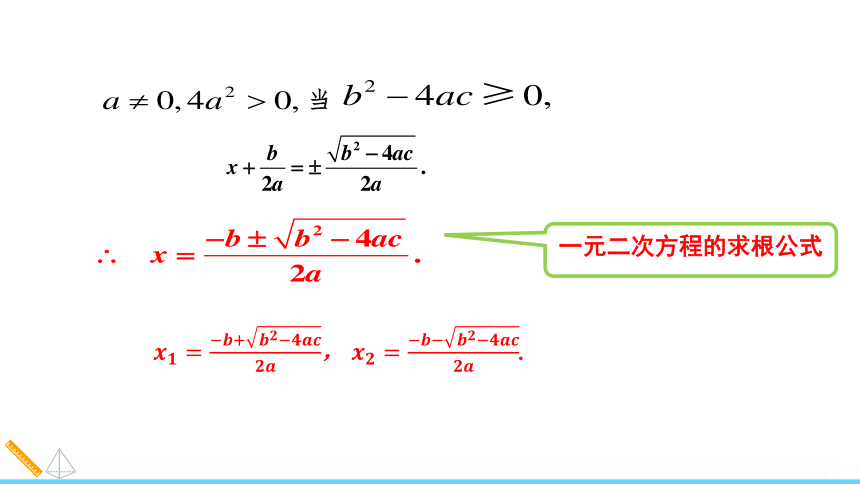
一元二次方程的求根公式
当
, .
由上可知,一元二次方程
的根由方程的系数a,b,c确定.因此,解一元二次方程时,可以先将方程化为一般形式 ,当 时,将a,b,c 代入式子 ,就得到方程的根,这个式子叫做一元二次方程的求根公式,利用它解一元二次方程的方法叫做公式法,由求根公式可知,一元二次方程最多有两个实数根.
当 b-4ac <0 时,方程有实数根吗?
公式法的概念
解:∵a=1,b=-4,c=-7,
∴b2-4ac=(-4)2-4×1×(-7)=44>0.
例 用公式法解方程:
公式法解方程
(1)x2-4x-7=0;
∴
典例精析
解:
则方程有两个相等的实数根:
(2)2x2-2 x+1=0;
【思考】这里的a、b、c的值分别是什么?
解:原方程可化为 .
则方程有两个不相等的实数根
(3)5x2-3x=x+1;
.
.
解:原方程可化为 .
方程无实数根.
(4)x2+17=8x.
.
(1)当
时,一元二次方程有两个不
相等的实数根;
(2)当
时,一元二次方程有两个相
等的实数根;
(3)当
时,一元二次方程没有实
数根.
方法点拨
用公式法解一元二次方程的一般步骤
1. 将方程化成一般形式,并写出a,b,c 的值.
2. 求出 的值.
3. (1)当 >0 时,代入求根公式 :
写出一元二次方程的根.
(2)当 =0时,代入求根公式:
写出一元二次方程的根.
(3)当 <0时,方程无实数根.
用公式法解方程:
解:a=3, b=-6, c=-2,
=b2-4ac=(-6)2-4×3×(-2)=60.
巩固练习
用公式法解下列方程:
(1) x2+x-1 = 0 (2)x2-2
(3) 2x2-2x+1 = 0
x+3 = 0
观察上面解一元二次方程的过程,一元二次方程的根的情况与一元二次方程中二次项系数、一次项系数及常数项有关吗?能否根据这个关系不解方程得出方程的解的情况呢?
新知二 一元二次方程的根的情况
合作探究
【思考】
不解方程,你能判断下列方程根的情况吗?
⑴ x2+2x-8 = 0
⑵ x2 = 4x-4
⑶ x2-3x = -3
(3)没有实数根.
答案:(1)有两个不相等的实数根;
(2)有两个相等的实数根;
【发现】b2-4ac的符号决定着方程的解.
(2)当b2-4ac=0时,有两个相等的实数根:
(1)当b2-4ac>0 时,有两个不等的实数根:
(3)当b2-4ac<0时,没有实数根.
一般的,式子 b2-4ac 叫做一元二次方程根的判别式,通常用希腊字母“ ”来表示,即 =b2-4ac.
一元二次方程的根的情况
若已知一个一元二次方程的根的情况,是否能得到判别式的值的符号呢?
当一元二次方程有两个不相等的实数根时, b2-4ac >0;
当一元二次方程有两个相等的实数根时, b2-4ac = 0;
当一元二次方程没有实数根时, b2-4ac < 0.
【注意】
一元二次方程的根的情况
例1 不解方程,判断下列方程根的情况:
解:a=﹣1,b= ,c=﹣6,
△= b2-4ac
=24-4×(﹣1)×(-6)=0.
该方程有两个相等的实数根.
解: 移项,得 x2+4x-2=0,
a=1,b=4 ,c=﹣2,
△= b2-4ac
=16-4×1×(-2)=24>0.
该方程有两个不相等的实数根.
利用判别式识别一元二次方程的根的情况
(2)x2+4x=2;
(1) ;
典例精析
(3)4x2+1=-3x;
解:移项,得4x2+3x+1=0,
a=4,b=3 ,c=1,
∵ △= b2-4ac
=9-4×4×1=-7<0.
∴该方程没有实数根.
解:a=1,b=-2m ,c=4(m-1),
∵ △= b2-4ac
=(-2m) -4×1×4(m-1)
=4m2-16(m-1)
=4m2-16m+16
=(2m-4)2≥0.
∴该方程有两个实数根.
(4)x -2mx+4(m-1)=0.
(2)方程ax2+bx+c=0(a≠0)有实数根,那么总成立的式
子是( )
A. b -4ac>0 B. b -4ac<0
C. b -4ac≤0 D. b -4ac≥0
(1)下列方程中,没有实数根的方程是( )
A.x =9 B.4x =3(4x-1)
C.x(x+1)=1 D.2y +6y+7=0
D
D
选一选.
巩固练习
例2 m为何值时,关于x的一元二次方程 2x2-(4m+1)x+2m2-1=0:
(1)有两个不相等的实数根?(2)有两个相等的实数根?
(3)没有实数根?
解:a=2,b=-(4m+1),c=2m2-1,
b2-4ac=〔-(4m+1)〕2-4×2(2m2-1)=8m+9.
(1)若方程有两个不相等的实数根,则b2-4ac >0,即8m+9>0 ∴m>
(2)若方程有两个相等的实数根,则b2-4ac=0即8m+9=0 ∴m=
(3)若方程没有实数根,则b2-4ac<0即8m+9<0, ∴m<
∴当m> 时,方程有两个不相等的实数根;当m= 时,
方程有两个相等的实数根;当m< 时,方程没有实数根.
利用判别式求字母的值或取值范围
典例精析
m为任意实数,试说明关于x的方程x2-(m-1)x-3(m+3)=0恒有两个不相等的实数根.
解:
∵不论m取任何实数,总有(m+5)2≥0,
∴b2-4ac=(m+5)2+12≥12>0,
∴不论m取任何实数,上述方程总有两个不相等的实数根.
巩固练习
1.方程x2-4x+4=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.有一个实数
D.没有实数根
B
课堂练习
2. 关于x的一元二次方程kx2-2x-1=0有两个不等 的实根,则k的取值范围是 ( )
A. k>-1 B. k>-1 且k≠ 0
C. k<1 D. k<1 且k≠0
B
3. 已知x2+2x=m-1没有实数根,求证:x2+mx=1-2m必有两个不相等的实数根.
证明:∵ 没有实数根,
∴ 4-4(1-m)<0, ∴m<0.
对于方程 x2+mx=1-2m ,即 .
,∵ ,∴ △>0.
∴x2+mx=1-2m必有两个不相等的实数根.
公式法
定义
把各系数直接带入求根公式的解一元二次方程的方法.
步骤
一化成一般形式, 并写出a,b,c的值;
二求出b2-4ac的值;
三;
四写出方程的解:x1, x2.
应用
用判别式△= b2-4ac判定一元二次方程根的情况.
归纳新知
1.(2020·安徽)下列方程中,有两个相等实数根的是( )
A.x2+1=2x B.x2+1=0
C.x2-2x=3 D.x2-2x=0
2.下列关于x的方程ax2-bx=0(a,b是不为0的常数)的根的情况
判断正确的是( )
A.无实数根
B.有两个不等的实数根
C.有两个相等的实数根
D.有且只有一个实数根
A
B
课后练习
3.(2020·吉林)一元二次方程x2+3x-1=0根的判别式的值为________.
4.(2020·辽阳)若关于x的一元二次方程x2+2x-k=0无实数根,
则k的取值范围是____.
k<-1
13
5.(教材P17T4变式)利用判别式判断下列方程的根的情况:
(1)9x2-6x+1=0;
解:∵a=9,b=-6,c=1,∴Δ=(-6)2-4×9×1=0,
∴此方程有两个相等的实数根
(2)8x2+4x=-3;
解:化为一般形式为8x2+4x+3=0,∵a=8,b=4,c=3,
∴Δ=42-4×8×3=-80<0,∴此方程没有实数根
(3)2(x2-1)+5x=0.
解:化为一般形式为2x2+5x-2=0,∵a=2,b=5,c=-2,
∴Δ=52-4×2×(-2)=41>0,∴此方程有两个不相等的实数根
B
A
8.一元二次方程x2-x-6=0中,b2-4ac=_____,
可得x1=________,x2=________.
25
3
-2
9.用公式法解下列方程:
(1)x2-3x-2=0;
(2)8x2-8x+1=0;
10.已知m,n是方程x2-x-1=0的两个解,若m>n,则m的值应在( )
A.0和1之间 B.1和1.5之间
C.1.5和2之间 D.2和3之间
11.(2020·潍坊)关于x的一元二次方程x2+(k-3)x+1-k=0根的情况,
下列说法正确的是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.无法确定
C
A
12.关于x 的方程(a+1)x2-4x-1=0有实数根,
则a满足的条件是_________.
13.定义:如果关于x的一元二次方程ax2+bx+c=0(a≠0)
满足a+b+c=0,那么我们称这个方程为“凤凰”方程.
已知关于x的方程x2+mx+n=0是“凤凰”方程,
且有两个相等的实数根,则mn=____.
a≥-5
-2
14.已知关于x的一元二次方程x2-3x+a-1=0有实数根.
(1)求a的取值范围;
(2)当a为符合条件的最大整数时,求此时方程的解.
15.(教材P17T13变式)已知关于x的一元二次方程(x-3)(x-2)=|m|.
(1)求证:对于任意实数m,方程总有两个不等的实数根;
(2)若方程的一个根是1,求m的值及方程的另外一个根.
解:(1)原方程整理得x2-5x+6-|m|=0,
Δ=25-4(6-|m|)=1+4|m|.∵|m|≥0, ∴Δ>0.
∴原方程有两个不相等的实数根
(2)当x=1时,将x=1代入得1-5+6-|m|=0,∴m=±2.
当m=±2时,原方程可化为x2-5x+4=0,x1=1,x2=4,
∴方程的另外一个根为4
16.已知关于x的方程x2-2(m+2)x+m2+5=0没有实数根.
(1)求m的取值范围;
(2)试判断关于x的方程(m+5)x2-2(m+1)x+m=0的根的情况.
17.已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,
其中a,b,c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
解:(1)△ABC是等腰三角形.理由:∵x=-1是方程的根,
∴(a+c)×(-1)2-2b+(a-c)=0,∴a+c-2b+a-c=0,
∴a-b=0,∴a=b,∴△ABC是等腰三角形
(2)△ABC是直角三角形.。∵方程有两个相等的实数根,
∴(2b)2-4(a+c)(a-c)=0,∴4b2-4a2+4c2=0,
∴a2=b2+c2,∴△ABC是直角三角形
(3)当a=b=c时,可整理为2ax2+2ax=0,∴x2+x=0,解得x1=0,x2=-1
再 见
同课章节目录
