山东省潍坊市2021-2022学年高二上学期期中考试数学试题(Word版含答案)
文档属性
| 名称 | 山东省潍坊市2021-2022学年高二上学期期中考试数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 799.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 09:50:23 | ||
图片预览




文档简介
潍坊市2021-2022学年高二上学期期中考试数学 试 题
本试卷分第 卷(选择题) 和第Ⅱ 卷(非选择题)两部分, 满分 150 分。考试用时 120 分钟。
注意事项:
答题前, 考生务必用 毫米黑色签字笔将姓名、座号、准考证号、班级和科类填写在答 题卡和答题纸规定的位置上。
第 卷每小题选出答案后, 用 铅笔把答题卡上对应题目的答案标号涂黑, 如需改 动, 用橡皮擦干净后, 再选涂其它答案标号。
第 II 卷必须用 毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应 的位置, 不能写在试卷上; 如需改动, 先划掉原来的答案, 然后再写上新的答案; 不能使用涂改 液、胶带纸、修正带。不按以上要求作答的答案无效。
填空题请直接填写答案, 解答题应写出文字说明、证明过程或演算步骤。
第 卷 分
一、单项选择题: 本大题共 8 小题, 每小题 5 分, 在每小题给出的四个选项中, 只有一项是符合 题目要求的.
直线 的倾斜角为
A.
B.
C.
D.
已知直线 不在平面 内, 则“ ”是“直线 上存在两个点到平面 的距离相等”的
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
在平面直角坐标系中, 直线 绕它与 轴的交点 按顺时针方向旋转 所得的直线方程是
A.
B.
C.
D.
若直线 与直线 垂直, 则
A.
B.
C.
D.
半径为 4 的半圆卷成一个圆雉, 则该圆锥的体积为
A.
B.
C.
D.
圆 上的点 关于直线 的对称点仍在圆 上, 且该圆的半径为 , 则圆 的方程为
A.
B.
C. 或
D. 或
攒尖是古代中国建筑中屋顶的一种结构形式, 宋代称为撮尖, 清代称攒尖. 依其平面有圆形攒尖、三角攒尖、四角攒尖、六角 攒尖等, 也有单檐和重檐之分, 多见于亭阁式建筑. 如图所示, 某园林建筑的屋顶为六角攒尖, 它的主要部分的轮廓可近似看 作一个正六棱锥, 若此正六棱雉的侧棱长为 2 , 且与底面所成的 角为 , 则此正六棱锥的体积为
A.
B.
C.
D. .
若直线 与曲线 . 仅有一个公共点, 则 的取值范围是
A.
B.
C.
D.
二、多项选择题: 本题共 4 小题,每小题 5 分, 共 20 分. 在每小题给出的选项中, 有多项符合题 目要求. 全部选对的得 5 分, 部分选对的得 2 分, 有选错的得 0 分.
直线 与圆 的大致图像可能正确的是
下列命题中, 正确的结论有
A. 如果一个角的两边与另一个角的两边分别平行, 那么这两个角相等
B. 如果两条相交直线和另两条相交直线分别平行, 那么这两组直线所成的锐角 (或直 角)相等
C. 如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补
D. 如果两条直线同吋平行于第三条直线, 那公这两条直线互相平行
已知直线 , 则下列结论正确的是
A. 存在实数 , 使得直线 与直线 垂直
B. 存在实数 , 使得直线 与直线 平行
C. 存在实数 , 使得点 . 到直线 的距离为 4
D. 存在实数 , 使得以线段 为直径的圆上的点到直线 的最大距离为
“阿基米德多面体”也称为半正多面体, 是由边数不全相同的正多边形为面围成的多面 体, 它体现了数学的对称美. 如图, 将正方体沿交于一顶点的三条棱的中点截去一个三棱锥, 共截去八个三棱锥,得到的半正多面体的表面积为 , 则关于该半正多面 体的下列说法中正确的是
A.
B. 该半正多面体的外接球的表面积为
C. 与平面 所成的角为
D. 与 所成的角是 的棱共有 16 条
(第Ⅱ 卷 90 分
三、填空题: (本大题共 4 小题, 每小题 5 分, 共 20 分, 把正确答案填在答题卡相应题的横线上)
过 两点的直线 的斜率为________.
已知空间向量 , 若 , 则
过点 的光线 经 轴反射后与圆 . 相切, 则
已知点 是空间直角坐标系 内一点, 则点 关于 轴的对称点 的 坐标为 ________. 若点 在平面 上的射影为 , 则四面体 的体积 为________.
四、解答题: 共 70 分. 解答出文字说明、证明过程或演算步骤.
(本小题满分 10 分)
已知 的三个顶点 , 边 的中线所在直线方程 为 ,
(1)求实数 ;
(2)试判断点 与以线段 为直径的圆的位置关系, 并说明理由.
(本小题满分 12 分)
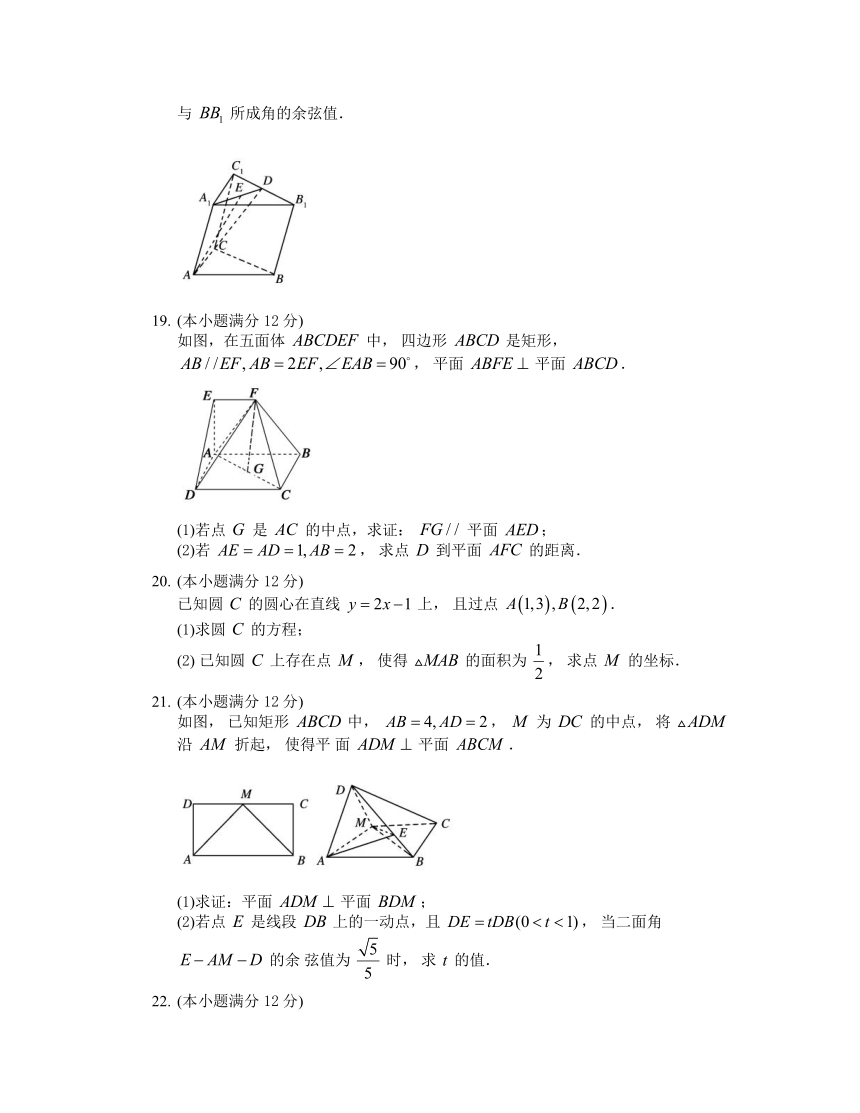
如图, 三棱柱 为 的中点, , 设
(1)试用 表示向量 ;
(2)若 ,异面直线 与 所成角的余弦值.
(本小题满分 12 分)
如图,在五面体 中, 四边形 是矩形, , 平面 平面 .
(1)若点 是 的中点,求证: 平面 ;
(2)若 , 求点 到平面 的距离.
(本小题满分 12 分)
已知圆 的圆心在直线 上, 且过点 .
(1)求圆 的方程;
(2) 已知圆 上存在点 , 使得 的面积为 , 求点 的坐标.
(本小题满分 12 分)
如图, 已知矩形 中, , 为 的中点, 将 沿 折起, 使得平 面 平面 .
(1)求证:平面 平面 ;
(2)若点 是线段 上的一动点,且 , 当二面角 的余 弦值为 时, 求 的值.
(本小题满分 12 分)
已知圆 的圆心与点 关于直线 对称, 且圆 与 轴相切于原 点 .
(1)求圆 的方程;
(2)过原点 的两条直线与圆 分别交于 两点, 直线 的斜率之积为 , 为垂足, 是否存在定点 , 使得 为定值, 若存在, 求出 点坐标; 若不存在, 说明理由.
本试卷分第 卷(选择题) 和第Ⅱ 卷(非选择题)两部分, 满分 150 分。考试用时 120 分钟。
注意事项:
答题前, 考生务必用 毫米黑色签字笔将姓名、座号、准考证号、班级和科类填写在答 题卡和答题纸规定的位置上。
第 卷每小题选出答案后, 用 铅笔把答题卡上对应题目的答案标号涂黑, 如需改 动, 用橡皮擦干净后, 再选涂其它答案标号。
第 II 卷必须用 毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应 的位置, 不能写在试卷上; 如需改动, 先划掉原来的答案, 然后再写上新的答案; 不能使用涂改 液、胶带纸、修正带。不按以上要求作答的答案无效。
填空题请直接填写答案, 解答题应写出文字说明、证明过程或演算步骤。
第 卷 分
一、单项选择题: 本大题共 8 小题, 每小题 5 分, 在每小题给出的四个选项中, 只有一项是符合 题目要求的.
直线 的倾斜角为
A.
B.
C.
D.
已知直线 不在平面 内, 则“ ”是“直线 上存在两个点到平面 的距离相等”的
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
在平面直角坐标系中, 直线 绕它与 轴的交点 按顺时针方向旋转 所得的直线方程是
A.
B.
C.
D.
若直线 与直线 垂直, 则
A.
B.
C.
D.
半径为 4 的半圆卷成一个圆雉, 则该圆锥的体积为
A.
B.
C.
D.
圆 上的点 关于直线 的对称点仍在圆 上, 且该圆的半径为 , 则圆 的方程为
A.
B.
C. 或
D. 或
攒尖是古代中国建筑中屋顶的一种结构形式, 宋代称为撮尖, 清代称攒尖. 依其平面有圆形攒尖、三角攒尖、四角攒尖、六角 攒尖等, 也有单檐和重檐之分, 多见于亭阁式建筑. 如图所示, 某园林建筑的屋顶为六角攒尖, 它的主要部分的轮廓可近似看 作一个正六棱锥, 若此正六棱雉的侧棱长为 2 , 且与底面所成的 角为 , 则此正六棱锥的体积为
A.
B.
C.
D. .
若直线 与曲线 . 仅有一个公共点, 则 的取值范围是
A.
B.
C.
D.
二、多项选择题: 本题共 4 小题,每小题 5 分, 共 20 分. 在每小题给出的选项中, 有多项符合题 目要求. 全部选对的得 5 分, 部分选对的得 2 分, 有选错的得 0 分.
直线 与圆 的大致图像可能正确的是
下列命题中, 正确的结论有
A. 如果一个角的两边与另一个角的两边分别平行, 那么这两个角相等
B. 如果两条相交直线和另两条相交直线分别平行, 那么这两组直线所成的锐角 (或直 角)相等
C. 如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补
D. 如果两条直线同吋平行于第三条直线, 那公这两条直线互相平行
已知直线 , 则下列结论正确的是
A. 存在实数 , 使得直线 与直线 垂直
B. 存在实数 , 使得直线 与直线 平行
C. 存在实数 , 使得点 . 到直线 的距离为 4
D. 存在实数 , 使得以线段 为直径的圆上的点到直线 的最大距离为
“阿基米德多面体”也称为半正多面体, 是由边数不全相同的正多边形为面围成的多面 体, 它体现了数学的对称美. 如图, 将正方体沿交于一顶点的三条棱的中点截去一个三棱锥, 共截去八个三棱锥,得到的半正多面体的表面积为 , 则关于该半正多面 体的下列说法中正确的是
A.
B. 该半正多面体的外接球的表面积为
C. 与平面 所成的角为
D. 与 所成的角是 的棱共有 16 条
(第Ⅱ 卷 90 分
三、填空题: (本大题共 4 小题, 每小题 5 分, 共 20 分, 把正确答案填在答题卡相应题的横线上)
过 两点的直线 的斜率为________.
已知空间向量 , 若 , 则
过点 的光线 经 轴反射后与圆 . 相切, 则
已知点 是空间直角坐标系 内一点, 则点 关于 轴的对称点 的 坐标为 ________. 若点 在平面 上的射影为 , 则四面体 的体积 为________.
四、解答题: 共 70 分. 解答出文字说明、证明过程或演算步骤.
(本小题满分 10 分)
已知 的三个顶点 , 边 的中线所在直线方程 为 ,
(1)求实数 ;
(2)试判断点 与以线段 为直径的圆的位置关系, 并说明理由.
(本小题满分 12 分)
如图, 三棱柱 为 的中点, , 设
(1)试用 表示向量 ;
(2)若 ,异面直线 与 所成角的余弦值.
(本小题满分 12 分)
如图,在五面体 中, 四边形 是矩形, , 平面 平面 .
(1)若点 是 的中点,求证: 平面 ;
(2)若 , 求点 到平面 的距离.
(本小题满分 12 分)
已知圆 的圆心在直线 上, 且过点 .
(1)求圆 的方程;
(2) 已知圆 上存在点 , 使得 的面积为 , 求点 的坐标.
(本小题满分 12 分)
如图, 已知矩形 中, , 为 的中点, 将 沿 折起, 使得平 面 平面 .
(1)求证:平面 平面 ;
(2)若点 是线段 上的一动点,且 , 当二面角 的余 弦值为 时, 求 的值.
(本小题满分 12 分)
已知圆 的圆心与点 关于直线 对称, 且圆 与 轴相切于原 点 .
(1)求圆 的方程;
(2)过原点 的两条直线与圆 分别交于 两点, 直线 的斜率之积为 , 为垂足, 是否存在定点 , 使得 为定值, 若存在, 求出 点坐标; 若不存在, 说明理由.
同课章节目录
