北师大版七年级数学上册第六章《数据的收集与整理》复习课件(17张)
文档属性
| 名称 | 北师大版七年级数学上册第六章《数据的收集与整理》复习课件(17张) |  | |
| 格式 | ppt | ||
| 文件大小 | 375.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 22:45:56 | ||
图片预览






文档简介
(共17张PPT)
第六章
数据的收集与整理
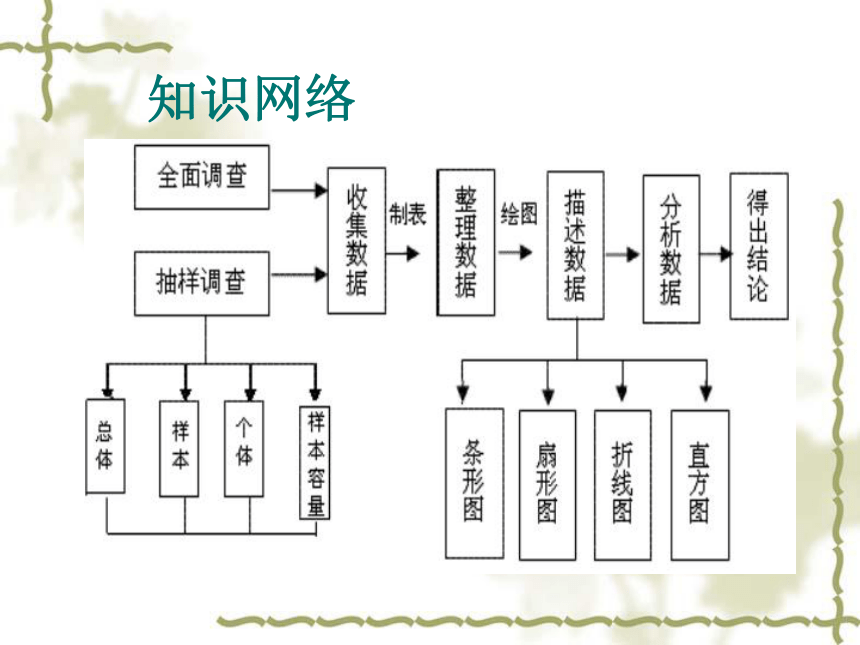
知识网络
全面调查与抽样调查
调查的方式有两种:全面调查和抽样调查: 1.全面调查:考察全面对象的调查叫全面调查. 全面调查也称作普查,调查的方法有:问卷调查、访问调查、电话调查等. 全面调查的步骤: (1)收集数据; (2)整理数据(划记法); (3)描述数据(条形图或扇形图等). 2.抽样调查:
若调查时因考察对象牵扯面较广,调查范围大,不宜采用全面调查,因此,采用抽样调查. 抽样调查只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况. 抽样调查的意义: (1)减少统计的工作量; (2)抽样调查是实际工作中应用非常广泛的一种调查方式,它是总体中抽取样本进行调查,根据样本来估计总体的一种调查.
总体、样本的概念
1.总体:要考察的全体对象称为总体.
2.个体:组成总体的每一个考察对象称为个体.
3.样本:被抽取的那些个体组成一个样本.
4.样本容量:样本中个体的数目叫样本容量(不带单位).
注意:为了使样本能较好地反映总体的情况,除了要有
合适的样本容量外,抽取时还要尽量使每一个个体都有
同等的机会被抽到.
3.判断全面调查和抽样调查的方法
①全面调查是对考察对象的全面调查,它要求对考察范围内所有个体进行一个不漏的逐个准确统计;而抽样调查则是对总体中的部分个体进行调查,以样本来估计总体的情况. ②注意区分“总体”和“部分”在表述上的差异. 在调查实际生活中的相关问题时,要灵活处理,既要考虑问题本身的需要,又要考虑实现的可能性和所付出代价的大小.
数据的表示:
表格、条形统计图、扇形统计图、折线统计图、频数直方图。
制作扇形统计图的步骤:
(1)求出全体即总量.
(2)计算出百分比
(3)求出圆心角度数.圆心角度数=百分比×360°
(4)画一个圆,用量角器量出角度画半径,画出扇形统计图.在每个
扇形上标明所代表部分的名称、百分比.
(5)写清统计图的标题、名称.
制作频数直方图的步骤:
(1)找出所有数据中的最大值和最小值,并算出它们的差
(2)决定组距和组数.
(3)确定分点
(4)列出频数分布表
(5)画频数分布直方图.
统计图的特征:
条形统计图:条形统计图能清楚地表示 出每个项目
的具体数目
折线统计图:能清楚的看出每个项目的变化情况及
变化趋势。
扇形统计图:扇形统计图能清楚地表 示出各部分
在总体中所 占的百分比
绘制统计图时应该注意的问题:
1、在绘制条形统计图时,纵坐标上的起始值应从“0”开始,从而避免造成“误导” 、引 起 “错觉” ;
2、通过两幅折线统计图的认识, 在比较两个统计量的变化趋势时, 应注意横 (纵) 坐标的一致性;
3、扇形统计图只能显示各部分在总体中所占的百分比,两个扇形统计图中的 相同研究对象无法直接比较大小.
经典例题透析
1.学校需要了解有多少学生已经患上近视,下面哪些抽样方式是合适的,说明你的理由。 (1)在学校门口通过观察统计有多少学生是佩戴眼镜的;
(2)在低年级学生中随机抽取一个班作调查;
(3)从每个年级的每个班级都随机抽取几个学生作调查。
类型一:考查基本概念
1:为了了解2009年河南省中考数学考试情况,从所有考生中抽取600名考生的成绩进行考查,指出该考查中的总体和样本分别是什么?
思路点拨:从概念上来看,总体即全部考查对象,样本是一部分考查对象,还要注意考查的对象是数量指标.
解析:总体是2009年河南省参加中考考试的所有考生的数学成绩;样本是抽取的600名考生的数学成绩.
总结升华:统计中的研究对象是数据,而不是具体的人或物. 在叙述总体和样本时,要注意他们的范围和数量指标.
举一反三: 【变式】2007年某县共有4591人参加中考,为了考查这4591名学生的外语成绩,从中抽取了80名学生成绩进行调查,以下说法不正确的是( ). A.4591名学生的外语成绩是总体; B.此题是抽样调查; C.样本是80名学生的外语成绩; D.样本是被调查的80名学生.
【答案】D.
类型二: 调查方法的考查
2:下列调查中,适合用普查(全面调查)方法的是(D. ). A.电视机厂要了解一批显像管的使用寿命; B.要了解我市居民的环保意识; C.要了解我市“阳山水蜜桃”的甜度和含水量; D.要了解某校数学教师的年龄状况
思路点拨:A、B、C工作量太大,太复杂,只能作抽样调查,而D可以作普查,即全面调查. 总结升华:在调查实际生活中的相关问题时,要灵活处理,既要考虑问题本身的需要,又要考虑实现的可能性和所付出代价的大小.
举一反三: 【变式】下列抽样调查中抽取的样本合适吗?为什么? (1)数学老师为了了解全班同学数学学习中存在的困难和问题,请数学成绩优秀的10名同学开座谈会; (2)在上海市调查我国公民的受教育程度; (3)在中学生中调查青少年对网络的态度; (4)调查每班学号为5的倍数的学生,以了解学校全体学生的身高和体重; (5)调查七年级中的两位同学,以了解全校学生的课外辅导用书的拥有量.
类型三:条形统计图和扇形统计图
3:某厂生产一种产品,图一是该厂第一季度三个月产量的统计图,图二是这三个月的产量占第一季度总量的比例分布统计图,统计员在制作图一、图二时漏填了部分数据.
根据上述信息,回答下列问题: (1)该厂第一季度哪一个月的
产量最高?__________月. (2)该厂一月份产量占第一
季度总产量的__________%. (3)该厂质检科从第一季度的
产品中随机抽样,抽检结果发现样品
的合格率为98%. 请你估计:该厂 第一季度大约生产了多
少件合格的产品?(写出解答过程)
举一反三:
【变式1】图中是甲、乙两户居民家庭全年各项支出的统计图.
根据统计图,下列对两户居民家庭教育支出占全年
总支出的百分比做出的判断中正确的是( ). A.甲户比乙户大;
B.乙户比甲户大;
C.甲、乙两户一样大;
D.无法确定哪一户大. 分析:从图甲中可以直接读出甲户居民家庭全年
的各项支出:衣着1200元,食品2000元,教育1200元,
其他1600元,故全年总支出为:
1200+2000+1200+1600=6000(元),
由此求出甲户教育支出占全年总支出的百分比为:
由图乙得知乙户居民的教育支出占全年总支出的百分比为25%,所以选B.
【变式2】
图中所示是北京奥运会、残奥会志愿者申请人来源的统计数据,请你计算:志愿者申请人的总数为__________万;其中“京外省区市”志愿者申请人数在总人数中所占的百分比约为__________%(精确到0.1%),它对应的扇形的圆心角约为__________(精确到度).
分析:由统计图可知,志愿者申请人的总数为: 2.8+2.2+77.2+29.2+0.7+0.2+0.3=112.6(万人).
其中“京外省区市”志愿者申请人数在
总人数中所占的百分比约为
,它所对应的扇形圆心角约为:360°×25.9%≈93°. 【答案】112.6;25.9;93°.
类型四: 频数分布直方图
4:一超市为了制定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如图所示的频数分布直方图(图中等待时间6分钟到7分钟表示大于或等于6分钟而小于7分钟,其他类同). 这个时间段内顾客等待时间不少于6分钟的人数为( ). A.5; B.7; C.16; D.33.
思路点拨:本题主要考查频数分布直方
图的意义,由图易得这个时间段内顾
客等待时间不少于6分
钟的人数为
5+2=7人. 解析:B.
规律方法指导
通过本章的学习,使我们能够根据统计结果做出合理的判断和预测,体会统计对决策的作用,能比较清晰地表达自己的观点,进行交流;
认识到统计在社会生活及科学领域中的作用,并能解决一些简单的实际问题. 本章内容属于数学学科中的统计学范畴,在初中数学中占有重要的基础地位,是进一步学习统计和概率学的基础. 学习中要积极参与知识的探索过程,并且带着自己的看法、想法与其他同学交流,从中可获得更多的方法和自信. 加强统计思想、转化思想和数形结合思想的具体应用,在收集数据、描述数据的过程中,要求我们能及时把数据转化成统计图,从而实现信息转化;
在实际操作过程中,又能从统计图中扑捉有用的信息,充分发挥数形结合的作用.
第六章
数据的收集与整理
知识网络
全面调查与抽样调查
调查的方式有两种:全面调查和抽样调查: 1.全面调查:考察全面对象的调查叫全面调查. 全面调查也称作普查,调查的方法有:问卷调查、访问调查、电话调查等. 全面调查的步骤: (1)收集数据; (2)整理数据(划记法); (3)描述数据(条形图或扇形图等). 2.抽样调查:
若调查时因考察对象牵扯面较广,调查范围大,不宜采用全面调查,因此,采用抽样调查. 抽样调查只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况. 抽样调查的意义: (1)减少统计的工作量; (2)抽样调查是实际工作中应用非常广泛的一种调查方式,它是总体中抽取样本进行调查,根据样本来估计总体的一种调查.
总体、样本的概念
1.总体:要考察的全体对象称为总体.
2.个体:组成总体的每一个考察对象称为个体.
3.样本:被抽取的那些个体组成一个样本.
4.样本容量:样本中个体的数目叫样本容量(不带单位).
注意:为了使样本能较好地反映总体的情况,除了要有
合适的样本容量外,抽取时还要尽量使每一个个体都有
同等的机会被抽到.
3.判断全面调查和抽样调查的方法
①全面调查是对考察对象的全面调查,它要求对考察范围内所有个体进行一个不漏的逐个准确统计;而抽样调查则是对总体中的部分个体进行调查,以样本来估计总体的情况. ②注意区分“总体”和“部分”在表述上的差异. 在调查实际生活中的相关问题时,要灵活处理,既要考虑问题本身的需要,又要考虑实现的可能性和所付出代价的大小.
数据的表示:
表格、条形统计图、扇形统计图、折线统计图、频数直方图。
制作扇形统计图的步骤:
(1)求出全体即总量.
(2)计算出百分比
(3)求出圆心角度数.圆心角度数=百分比×360°
(4)画一个圆,用量角器量出角度画半径,画出扇形统计图.在每个
扇形上标明所代表部分的名称、百分比.
(5)写清统计图的标题、名称.
制作频数直方图的步骤:
(1)找出所有数据中的最大值和最小值,并算出它们的差
(2)决定组距和组数.
(3)确定分点
(4)列出频数分布表
(5)画频数分布直方图.
统计图的特征:
条形统计图:条形统计图能清楚地表示 出每个项目
的具体数目
折线统计图:能清楚的看出每个项目的变化情况及
变化趋势。
扇形统计图:扇形统计图能清楚地表 示出各部分
在总体中所 占的百分比
绘制统计图时应该注意的问题:
1、在绘制条形统计图时,纵坐标上的起始值应从“0”开始,从而避免造成“误导” 、引 起 “错觉” ;
2、通过两幅折线统计图的认识, 在比较两个统计量的变化趋势时, 应注意横 (纵) 坐标的一致性;
3、扇形统计图只能显示各部分在总体中所占的百分比,两个扇形统计图中的 相同研究对象无法直接比较大小.
经典例题透析
1.学校需要了解有多少学生已经患上近视,下面哪些抽样方式是合适的,说明你的理由。 (1)在学校门口通过观察统计有多少学生是佩戴眼镜的;
(2)在低年级学生中随机抽取一个班作调查;
(3)从每个年级的每个班级都随机抽取几个学生作调查。
类型一:考查基本概念
1:为了了解2009年河南省中考数学考试情况,从所有考生中抽取600名考生的成绩进行考查,指出该考查中的总体和样本分别是什么?
思路点拨:从概念上来看,总体即全部考查对象,样本是一部分考查对象,还要注意考查的对象是数量指标.
解析:总体是2009年河南省参加中考考试的所有考生的数学成绩;样本是抽取的600名考生的数学成绩.
总结升华:统计中的研究对象是数据,而不是具体的人或物. 在叙述总体和样本时,要注意他们的范围和数量指标.
举一反三: 【变式】2007年某县共有4591人参加中考,为了考查这4591名学生的外语成绩,从中抽取了80名学生成绩进行调查,以下说法不正确的是( ). A.4591名学生的外语成绩是总体; B.此题是抽样调查; C.样本是80名学生的外语成绩; D.样本是被调查的80名学生.
【答案】D.
类型二: 调查方法的考查
2:下列调查中,适合用普查(全面调查)方法的是(D. ). A.电视机厂要了解一批显像管的使用寿命; B.要了解我市居民的环保意识; C.要了解我市“阳山水蜜桃”的甜度和含水量; D.要了解某校数学教师的年龄状况
思路点拨:A、B、C工作量太大,太复杂,只能作抽样调查,而D可以作普查,即全面调查. 总结升华:在调查实际生活中的相关问题时,要灵活处理,既要考虑问题本身的需要,又要考虑实现的可能性和所付出代价的大小.
举一反三: 【变式】下列抽样调查中抽取的样本合适吗?为什么? (1)数学老师为了了解全班同学数学学习中存在的困难和问题,请数学成绩优秀的10名同学开座谈会; (2)在上海市调查我国公民的受教育程度; (3)在中学生中调查青少年对网络的态度; (4)调查每班学号为5的倍数的学生,以了解学校全体学生的身高和体重; (5)调查七年级中的两位同学,以了解全校学生的课外辅导用书的拥有量.
类型三:条形统计图和扇形统计图
3:某厂生产一种产品,图一是该厂第一季度三个月产量的统计图,图二是这三个月的产量占第一季度总量的比例分布统计图,统计员在制作图一、图二时漏填了部分数据.
根据上述信息,回答下列问题: (1)该厂第一季度哪一个月的
产量最高?__________月. (2)该厂一月份产量占第一
季度总产量的__________%. (3)该厂质检科从第一季度的
产品中随机抽样,抽检结果发现样品
的合格率为98%. 请你估计:该厂 第一季度大约生产了多
少件合格的产品?(写出解答过程)
举一反三:
【变式1】图中是甲、乙两户居民家庭全年各项支出的统计图.
根据统计图,下列对两户居民家庭教育支出占全年
总支出的百分比做出的判断中正确的是( ). A.甲户比乙户大;
B.乙户比甲户大;
C.甲、乙两户一样大;
D.无法确定哪一户大. 分析:从图甲中可以直接读出甲户居民家庭全年
的各项支出:衣着1200元,食品2000元,教育1200元,
其他1600元,故全年总支出为:
1200+2000+1200+1600=6000(元),
由此求出甲户教育支出占全年总支出的百分比为:
由图乙得知乙户居民的教育支出占全年总支出的百分比为25%,所以选B.
【变式2】
图中所示是北京奥运会、残奥会志愿者申请人来源的统计数据,请你计算:志愿者申请人的总数为__________万;其中“京外省区市”志愿者申请人数在总人数中所占的百分比约为__________%(精确到0.1%),它对应的扇形的圆心角约为__________(精确到度).
分析:由统计图可知,志愿者申请人的总数为: 2.8+2.2+77.2+29.2+0.7+0.2+0.3=112.6(万人).
其中“京外省区市”志愿者申请人数在
总人数中所占的百分比约为
,它所对应的扇形圆心角约为:360°×25.9%≈93°. 【答案】112.6;25.9;93°.
类型四: 频数分布直方图
4:一超市为了制定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如图所示的频数分布直方图(图中等待时间6分钟到7分钟表示大于或等于6分钟而小于7分钟,其他类同). 这个时间段内顾客等待时间不少于6分钟的人数为( ). A.5; B.7; C.16; D.33.
思路点拨:本题主要考查频数分布直方
图的意义,由图易得这个时间段内顾
客等待时间不少于6分
钟的人数为
5+2=7人. 解析:B.
规律方法指导
通过本章的学习,使我们能够根据统计结果做出合理的判断和预测,体会统计对决策的作用,能比较清晰地表达自己的观点,进行交流;
认识到统计在社会生活及科学领域中的作用,并能解决一些简单的实际问题. 本章内容属于数学学科中的统计学范畴,在初中数学中占有重要的基础地位,是进一步学习统计和概率学的基础. 学习中要积极参与知识的探索过程,并且带着自己的看法、想法与其他同学交流,从中可获得更多的方法和自信. 加强统计思想、转化思想和数形结合思想的具体应用,在收集数据、描述数据的过程中,要求我们能及时把数据转化成统计图,从而实现信息转化;
在实际操作过程中,又能从统计图中扑捉有用的信息,充分发挥数形结合的作用.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
