2021--2022学年人教版七年级数学上册4.4课题学习:设计制作长方体形状的包装纸盒专项训练题 (word版含解析)
文档属性
| 名称 | 2021--2022学年人教版七年级数学上册4.4课题学习:设计制作长方体形状的包装纸盒专项训练题 (word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 10:20:17 | ||
图片预览

文档简介
4.4课题学习:设计制作长方体形状的包装纸盒专项训练题---2021--2022学年人教版(2012)七年级上学期
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.如图,是一个正方体的展开图,则展开前与C面相对的面是 ( )
A.A B.B
C.D D.F
2.如图正方体纸盒,展开后可以得到( )
A. B.
C. D.
3.下列各图中,可以是一个正方体的平面展开图的是( )
A. B. C. D.
4.下列图形中,圆锥的侧面展开图是( )
A. B. C. D.
5.在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列,正确的是
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
6.下列四个平面图形中,不能折叠成无盖长方体盒子的是( )
A. B. C.. D..
7.下面是“蒙牛”牌牛奶软包装盒,其表面展开图不正确的是( )
A. B. C. D.
8.如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A.A B.B C.C D.D
9.2015年,县委、县政府做出了“小微企业富民,大中企业强县,唱响千年文化,建设美好平定”的决策,如图是小明制作的一个正方体的表面展开图,原正方体中与“建”字所在的面相对的面上标的字是( )
A.美 B.好 C.平 D.定
10.下列展开图不能叠成无盖正方体的是:( )
A. B. C. D.
11.如图是一个正方体的表面展开图,这个正方体可能是( )
A. B. C. D.
12.用如图所示的纸片折成一个长方体纸盒,折得的纸盒是( ).
A. B. C. D.
13.某正方体的平面展开图如下图所示,这个正方体可能是下面四个选项中的( ).
A. B. C. D.
14.如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A. B. C. D.
评卷人得分
二、填空题
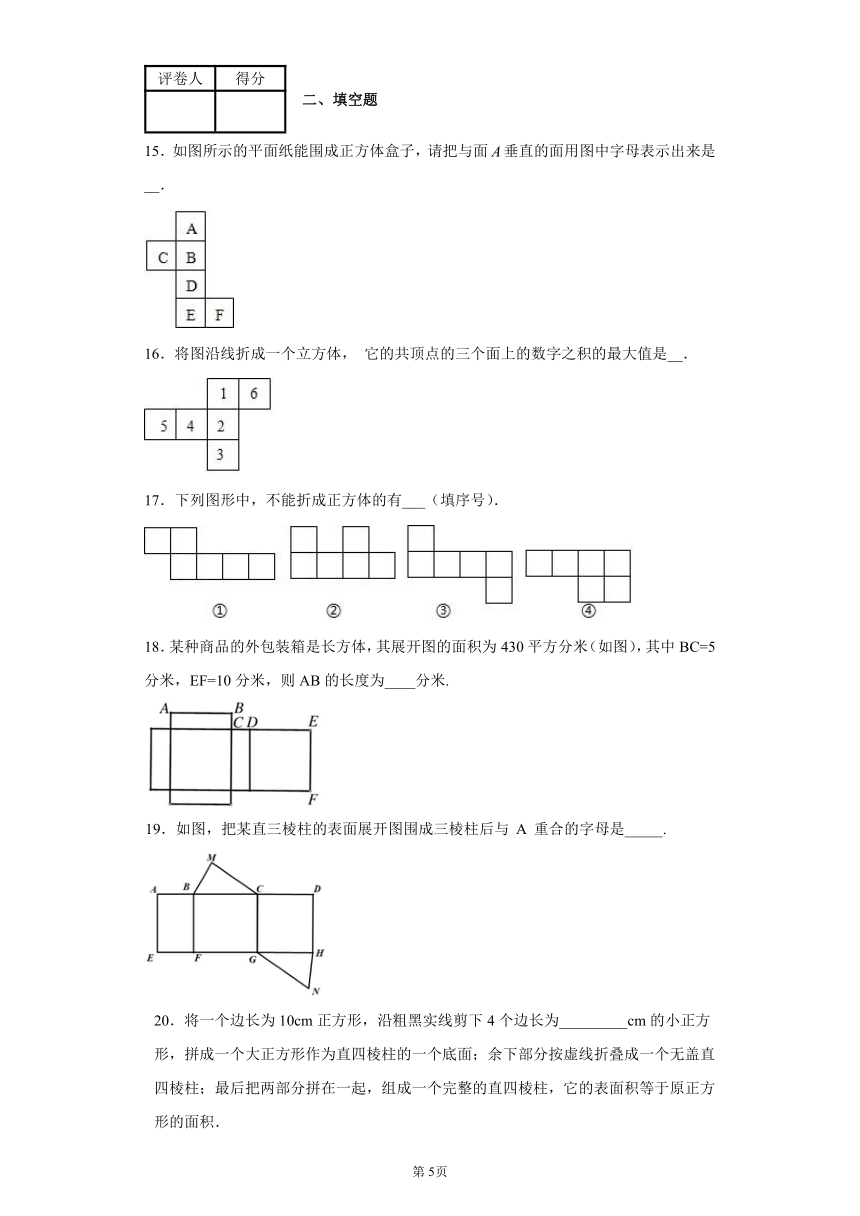
15.如图所示的平面纸能围成正方体盒子,请把与面垂直的面用图中字母表示出来是__.
16.将图沿线折成一个立方体, 它的共顶点的三个面上的数字之积的最大值是__.
17.下列图形中,不能折成正方体的有___(填序号).
18.某种商品的外包装箱是长方体,其展开图的面积为430平方分米(如图),其中BC=5分米,EF=10分米,则AB的长度为____分米.
19.如图,把某直三棱柱的表面展开图围成三棱柱后与 A 重合的字母是_____.
20.将一个边长为10cm正方形,沿粗黑实线剪下4个边长为_________cm的小正方形,拼成一个大正方形作为直四棱柱的一个底面;余下部分按虚线折叠成一个无盖直四棱柱;最后把两部分拼在一起,组成一个完整的直四棱柱,它的表面积等于原正方形的面积.
评卷人得分
三、解答题
21.如图,从上往下看A,B,C,D,E,F六个物体,分别能得到a,b,c,d,e,f哪个图形?把上下两行中对应的图形与物体连接起来.
22.如图是某长方体的展开图,它的棱长如图所示,请计算原长方体的表面积和体积.(结果用含的式子表示)
23.在学习《展开与折叠》这一课时,老师让同学们将准备好的正方体或长方体沿某些棱剪开,展开成平面图形.其中,阿中同学不小心多剪了一条棱,把一个长方体纸盒剪成了图①、图②两部分.根据你所学的知识,回答下列问题:
(1)阿中总共剪开了几条棱?
(2)现在阿中想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,他有几种粘贴方法?请在图①上画出粘贴后的图形(画出一种即可);
(3)已知图③是阿中剪开的图①的某些数据,求这个长方体纸盒的体积.
24. 如图是一个长方体的表面展开图,每个面上都标注了字母和数据,请根据要求回答
(1)如果A面在长方体的底部,那么 面会在上面;
(2)求这个长方体的表面积和体积.
25.下图是长方体的表面展开图,将它折叠成一个长方体.
()哪几个点与点重合?
()若,,,求这个长方体的表面积和体积.
26.如图所示是一个无盖的长方体纸盒的展开图,纸盒底面积为600 cm2.
(1)求纸盒的高为多少cm;
(2)展开图的周长为多少cm
27.综合与实践:某“综合与实践”小组开展了“正方体纸盒的制作”实践活动,他们利用长为,宽为长方形纸板制作出两种不同方案的正方体盒子, 请你动手操作验证并完成任务.(纸板厚度及接缝处忽略不计)
动手操作一:
如图1,若,按如图1所示的方式先在纸板四角剪去四个同样大小边长为的小正方形,再沿虚线折合起来就可以做成一个无盖的正方体纸盒.
问题解决:(1)此时,你发现与之间存在的数量关系为 .
动手操作二:
如图2,若,现在在纸板的四角剪去两个小正方形和两个小长方形恰好可以制作成一个有盖的正方体纸盒,其大小与(1)中无盖正方体大小一样.
拓展延伸:(2)请你在图2中画出你剪去的两个小正方形和两个小长方形(用阴影表示),折痕用虚线表示;
(3)此时,你发现与之间存在的数量关系为 ;若,求有盖正方体纸盒的表面积.
28.如图,将一个饮料包装盒剪开,铺平,纸样如图所示,包装盒的高为;设包装盒底面的长为.
(1)用表示包装盒底面的宽;
(2)用表示包装盒的表面积,并化简;
(3)若包装盒底面的长为,求包装盒的表面积.
试卷第1页,共3页
第1页
参考答案
1.D
解:相对的面的中间要相隔一个面,易得A、D相对;F、C相对,E、B相对.
故选:D.
2.D
解:A.两个蓝色圆所在的面折叠后是对面,不合题意;
B.白色圆与一个蓝色圆所在的面折叠后是对面,不合题意;
C.白色圆与一个蓝色圆所在的面折叠后是对面,不合题意;
D.白色圆与两个蓝色圆所在的面折叠后是相邻的面,符合题意;
故选:D.
3.C
【解】
A不是正方体的展开图,故不符合题意;
B不是正方体的展开图, 故不符合题意;
C是正方体的展开图,故符合题意;
D不是正方体的展开图,故不符合题意;
故选C.
4.A
【解】
圆锥的侧面展开图是光滑的曲面,是扇形.
故选:A.
5.C
【解】
甲:长方体的长为5cm,宽为3 cm,高为3 cm,容积为
乙:长方体的长为10 cm,宽为2 cm,高为2 cm,容积为
丙:长方体的长为6 cm,宽为4 cm,高为2 cm,容积为
所以,丙>甲>乙
故选C
6.C
【解】
选项A、B、D都能折叠成无盖的长方体盒子,选项C中,上下两底的长与侧面的边长不符,所以不能折叠成无盖的长方体盒子.
故选C.
7.B
【解析】因为只有选项B不能折成长方体,所以选项B不正确.
故选B
8.C
【详解】∵由图可知,实心圆点与空心圆点一定在紧相邻的三个侧面上,∴C符合题意.
故选C.
9.D
【解析】试题分析:本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.“设”与“号”是相对面,“建”与“定”是相对面,“美”与“平”是相对面.
10.C
【解析】:根据正方体的展开图的特点可以判断C不能叠成无盖正方体,故选C.
11.B
【解】
由展开图可知,围成正方体后,原来的四个小正方形组成正方体的一个面,其中是阴影,是空白.
故选B.
12.C
解:如图所示:
根据题意可知,的对面是,的对面是,的对面是,面阴影的短边与面阴影的一边重合.
故用如图所示的纸片折成一个长方体纸盒,折得的纸盒是C.
故选:C.
13.A
【解】
根据题意及图示只有A经过折叠后符合.
故选:A.
14.D
【解】
∵第三个图形是三角形,
∴将第三个图形展开,可得,即可排除答案A,
∵再展开可知两个短边正对着,
∴选择答案D,排除B与C.
故选D.
15.、、、
解:因为正方体的表面展开图,相对的面之间一定相隔一个正方形,
面“”与“”是相对面,它们互相平行,剩下的面都与面垂直;
所以:围成正方体盒子,与面垂直的面用图中字母表示出来是:、、、;
故答案为:、、、.
16.90
【解】
由题意可得,
6×3×5=90,
故答案为:90.
17.①②④
解:③可以折成正方体;
①、②、④折叠后有一个面重合,缺少一个底面,故不能折成正方体.
故答案为:①、②、④.
18.11
解:由题意得
2×(5AB+10AB+5×10)=430,
解得AB=11.
故答案为:11.
19.D 和 M
【解】
将图形沿BF,CG、BC折叠,可得A、D、M重合,故答案为D和M.
20.2.5
解:设粗黑实线剪下4个边长为xcm的小正方形,根据题意列方程
2x=10÷2
解得x=2.5cm,
故答案为2.5.
21.
【解】
22.表面积为,体积为
解:长方体表面积==,
长方体体积==.
23.(1)8条;(2)有4种粘贴方法,图形见解析;(3)这个长方形纸盒的体积为
解:(1)12-4=8(条)
因此,阿中总共剪开了8条棱.
(2)有4种粘贴方法.
如图,四种情况:
(3)设高为,则宽为,长为
∴
解得:
∴体积为:
答:这个长方形纸盒的体积为.
24.(1)F;(2)这个长方体的表面积是22(米2).这个长方体的体积是6(米3).
【解】(1)如图所示,A与F是对面,所以如果A面在长方体的底部,那么 F面会在上面;
故答案是:F;
(2)这个长方体的表面积是:2×(1×3+1×2+2×3)=22(米2).
这个长方体的体积是:1×2×3=6(米3).
25.(1)点F和点J;(2)112cm2, 64cm3
【解】
(1) 解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)由,,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
26.(1)高为10 cm;(2)展开图的周长为180cm.
【解析】(1)因为,纸盒的底面是由六个小正方形组成,
所以,每个小正方形的面积是=100(cm2).
所以,每个小正方形的边长为10 cm.
所以,高为10 cm.
(2)展开图的周长为18×10=180(cm).
27.(1);(2)见解析;(3)或或,600cm2
解:(1) (或)..
(2)所画图形如图所示(图形不唯一,画出一个即可).例如
(3) 据题意得,,
故或或
当时,.
由(1)可知制作的正方体的底面边长,
有盖正方体纸盒的表面积为.
28.(1)宽=;(2);(3)550.
解:(1)包装盒底面的宽为:(cm),
(2)包装盒的表面积为:
S=2×[(15-x)×15+15x+(15-x)×x]
=(cm2),
(3)包装盒底面的长为10cm,包装盒的表面积为:
S=2×[(15-10)×15+15×10+(15-10)×10]=550(cm2).
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.如图,是一个正方体的展开图,则展开前与C面相对的面是 ( )
A.A B.B
C.D D.F
2.如图正方体纸盒,展开后可以得到( )
A. B.
C. D.
3.下列各图中,可以是一个正方体的平面展开图的是( )
A. B. C. D.
4.下列图形中,圆锥的侧面展开图是( )
A. B. C. D.
5.在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列,正确的是
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
6.下列四个平面图形中,不能折叠成无盖长方体盒子的是( )
A. B. C.. D..
7.下面是“蒙牛”牌牛奶软包装盒,其表面展开图不正确的是( )
A. B. C. D.
8.如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A.A B.B C.C D.D
9.2015年,县委、县政府做出了“小微企业富民,大中企业强县,唱响千年文化,建设美好平定”的决策,如图是小明制作的一个正方体的表面展开图,原正方体中与“建”字所在的面相对的面上标的字是( )
A.美 B.好 C.平 D.定
10.下列展开图不能叠成无盖正方体的是:( )
A. B. C. D.
11.如图是一个正方体的表面展开图,这个正方体可能是( )
A. B. C. D.
12.用如图所示的纸片折成一个长方体纸盒,折得的纸盒是( ).
A. B. C. D.
13.某正方体的平面展开图如下图所示,这个正方体可能是下面四个选项中的( ).
A. B. C. D.
14.如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A. B. C. D.
评卷人得分
二、填空题
15.如图所示的平面纸能围成正方体盒子,请把与面垂直的面用图中字母表示出来是__.
16.将图沿线折成一个立方体, 它的共顶点的三个面上的数字之积的最大值是__.
17.下列图形中,不能折成正方体的有___(填序号).
18.某种商品的外包装箱是长方体,其展开图的面积为430平方分米(如图),其中BC=5分米,EF=10分米,则AB的长度为____分米.
19.如图,把某直三棱柱的表面展开图围成三棱柱后与 A 重合的字母是_____.
20.将一个边长为10cm正方形,沿粗黑实线剪下4个边长为_________cm的小正方形,拼成一个大正方形作为直四棱柱的一个底面;余下部分按虚线折叠成一个无盖直四棱柱;最后把两部分拼在一起,组成一个完整的直四棱柱,它的表面积等于原正方形的面积.
评卷人得分
三、解答题
21.如图,从上往下看A,B,C,D,E,F六个物体,分别能得到a,b,c,d,e,f哪个图形?把上下两行中对应的图形与物体连接起来.
22.如图是某长方体的展开图,它的棱长如图所示,请计算原长方体的表面积和体积.(结果用含的式子表示)
23.在学习《展开与折叠》这一课时,老师让同学们将准备好的正方体或长方体沿某些棱剪开,展开成平面图形.其中,阿中同学不小心多剪了一条棱,把一个长方体纸盒剪成了图①、图②两部分.根据你所学的知识,回答下列问题:
(1)阿中总共剪开了几条棱?
(2)现在阿中想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,他有几种粘贴方法?请在图①上画出粘贴后的图形(画出一种即可);
(3)已知图③是阿中剪开的图①的某些数据,求这个长方体纸盒的体积.
24. 如图是一个长方体的表面展开图,每个面上都标注了字母和数据,请根据要求回答
(1)如果A面在长方体的底部,那么 面会在上面;
(2)求这个长方体的表面积和体积.
25.下图是长方体的表面展开图,将它折叠成一个长方体.
()哪几个点与点重合?
()若,,,求这个长方体的表面积和体积.
26.如图所示是一个无盖的长方体纸盒的展开图,纸盒底面积为600 cm2.
(1)求纸盒的高为多少cm;
(2)展开图的周长为多少cm
27.综合与实践:某“综合与实践”小组开展了“正方体纸盒的制作”实践活动,他们利用长为,宽为长方形纸板制作出两种不同方案的正方体盒子, 请你动手操作验证并完成任务.(纸板厚度及接缝处忽略不计)
动手操作一:
如图1,若,按如图1所示的方式先在纸板四角剪去四个同样大小边长为的小正方形,再沿虚线折合起来就可以做成一个无盖的正方体纸盒.
问题解决:(1)此时,你发现与之间存在的数量关系为 .
动手操作二:
如图2,若,现在在纸板的四角剪去两个小正方形和两个小长方形恰好可以制作成一个有盖的正方体纸盒,其大小与(1)中无盖正方体大小一样.
拓展延伸:(2)请你在图2中画出你剪去的两个小正方形和两个小长方形(用阴影表示),折痕用虚线表示;
(3)此时,你发现与之间存在的数量关系为 ;若,求有盖正方体纸盒的表面积.
28.如图,将一个饮料包装盒剪开,铺平,纸样如图所示,包装盒的高为;设包装盒底面的长为.
(1)用表示包装盒底面的宽;
(2)用表示包装盒的表面积,并化简;
(3)若包装盒底面的长为,求包装盒的表面积.
试卷第1页,共3页
第1页
参考答案
1.D
解:相对的面的中间要相隔一个面,易得A、D相对;F、C相对,E、B相对.
故选:D.
2.D
解:A.两个蓝色圆所在的面折叠后是对面,不合题意;
B.白色圆与一个蓝色圆所在的面折叠后是对面,不合题意;
C.白色圆与一个蓝色圆所在的面折叠后是对面,不合题意;
D.白色圆与两个蓝色圆所在的面折叠后是相邻的面,符合题意;
故选:D.
3.C
【解】
A不是正方体的展开图,故不符合题意;
B不是正方体的展开图, 故不符合题意;
C是正方体的展开图,故符合题意;
D不是正方体的展开图,故不符合题意;
故选C.
4.A
【解】
圆锥的侧面展开图是光滑的曲面,是扇形.
故选:A.
5.C
【解】
甲:长方体的长为5cm,宽为3 cm,高为3 cm,容积为
乙:长方体的长为10 cm,宽为2 cm,高为2 cm,容积为
丙:长方体的长为6 cm,宽为4 cm,高为2 cm,容积为
所以,丙>甲>乙
故选C
6.C
【解】
选项A、B、D都能折叠成无盖的长方体盒子,选项C中,上下两底的长与侧面的边长不符,所以不能折叠成无盖的长方体盒子.
故选C.
7.B
【解析】因为只有选项B不能折成长方体,所以选项B不正确.
故选B
8.C
【详解】∵由图可知,实心圆点与空心圆点一定在紧相邻的三个侧面上,∴C符合题意.
故选C.
9.D
【解析】试题分析:本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.“设”与“号”是相对面,“建”与“定”是相对面,“美”与“平”是相对面.
10.C
【解析】:根据正方体的展开图的特点可以判断C不能叠成无盖正方体,故选C.
11.B
【解】
由展开图可知,围成正方体后,原来的四个小正方形组成正方体的一个面,其中是阴影,是空白.
故选B.
12.C
解:如图所示:
根据题意可知,的对面是,的对面是,的对面是,面阴影的短边与面阴影的一边重合.
故用如图所示的纸片折成一个长方体纸盒,折得的纸盒是C.
故选:C.
13.A
【解】
根据题意及图示只有A经过折叠后符合.
故选:A.
14.D
【解】
∵第三个图形是三角形,
∴将第三个图形展开,可得,即可排除答案A,
∵再展开可知两个短边正对着,
∴选择答案D,排除B与C.
故选D.
15.、、、
解:因为正方体的表面展开图,相对的面之间一定相隔一个正方形,
面“”与“”是相对面,它们互相平行,剩下的面都与面垂直;
所以:围成正方体盒子,与面垂直的面用图中字母表示出来是:、、、;
故答案为:、、、.
16.90
【解】
由题意可得,
6×3×5=90,
故答案为:90.
17.①②④
解:③可以折成正方体;
①、②、④折叠后有一个面重合,缺少一个底面,故不能折成正方体.
故答案为:①、②、④.
18.11
解:由题意得
2×(5AB+10AB+5×10)=430,
解得AB=11.
故答案为:11.
19.D 和 M
【解】
将图形沿BF,CG、BC折叠,可得A、D、M重合,故答案为D和M.
20.2.5
解:设粗黑实线剪下4个边长为xcm的小正方形,根据题意列方程
2x=10÷2
解得x=2.5cm,
故答案为2.5.
21.
【解】
22.表面积为,体积为
解:长方体表面积==,
长方体体积==.
23.(1)8条;(2)有4种粘贴方法,图形见解析;(3)这个长方形纸盒的体积为
解:(1)12-4=8(条)
因此,阿中总共剪开了8条棱.
(2)有4种粘贴方法.
如图,四种情况:
(3)设高为,则宽为,长为
∴
解得:
∴体积为:
答:这个长方形纸盒的体积为.
24.(1)F;(2)这个长方体的表面积是22(米2).这个长方体的体积是6(米3).
【解】(1)如图所示,A与F是对面,所以如果A面在长方体的底部,那么 F面会在上面;
故答案是:F;
(2)这个长方体的表面积是:2×(1×3+1×2+2×3)=22(米2).
这个长方体的体积是:1×2×3=6(米3).
25.(1)点F和点J;(2)112cm2, 64cm3
【解】
(1) 解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)由,,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
26.(1)高为10 cm;(2)展开图的周长为180cm.
【解析】(1)因为,纸盒的底面是由六个小正方形组成,
所以,每个小正方形的面积是=100(cm2).
所以,每个小正方形的边长为10 cm.
所以,高为10 cm.
(2)展开图的周长为18×10=180(cm).
27.(1);(2)见解析;(3)或或,600cm2
解:(1) (或)..
(2)所画图形如图所示(图形不唯一,画出一个即可).例如
(3) 据题意得,,
故或或
当时,.
由(1)可知制作的正方体的底面边长,
有盖正方体纸盒的表面积为.
28.(1)宽=;(2);(3)550.
解:(1)包装盒底面的宽为:(cm),
(2)包装盒的表面积为:
S=2×[(15-x)×15+15x+(15-x)×x]
=(cm2),
(3)包装盒底面的长为10cm,包装盒的表面积为:
S=2×[(15-10)×15+15×10+(15-10)×10]=550(cm2).
