2021-2022学年山东省青岛市莱西市七年级(上)期中数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2021-2022学年山东省青岛市莱西市七年级(上)期中数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1006.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 21:57:50 | ||
图片预览


文档简介
2021-2022学年山东省青岛市莱西市七年级第一学期期中数学试卷(五四学制)
一、选择题(本题满分24分,共8道小题,每小题3分)
1.下面图形中,是轴对称图形的是( )
A. B. C. D.
2.下列四个选项中,不是全等图形的是( )
A.
B.
C.
D.
3.下列三角形是直角三角形的是( )
A. B.
C. D.
4.一个三角形的两边长分别为3和8,则它的第三边长可能是( )
A.5 B.12 C.10 D.无法确定
5.下列条件不能得到等边三角形的是( )
A.有一个内角是60°的锐角三角形
B.有一个内角是60°的等腰三角形
C.顶角和底角相等的等腰三角形
D.腰和底边相等的等腰三角形
6.下列所叙述的图形中,全等的两个三角形是( )
A.含有45°角的两个直角三角形
B.腰相等的两个等腰三角形
C.边长相等的两个等边三角形
D.一个钝角对应相等的两个等腰三角形
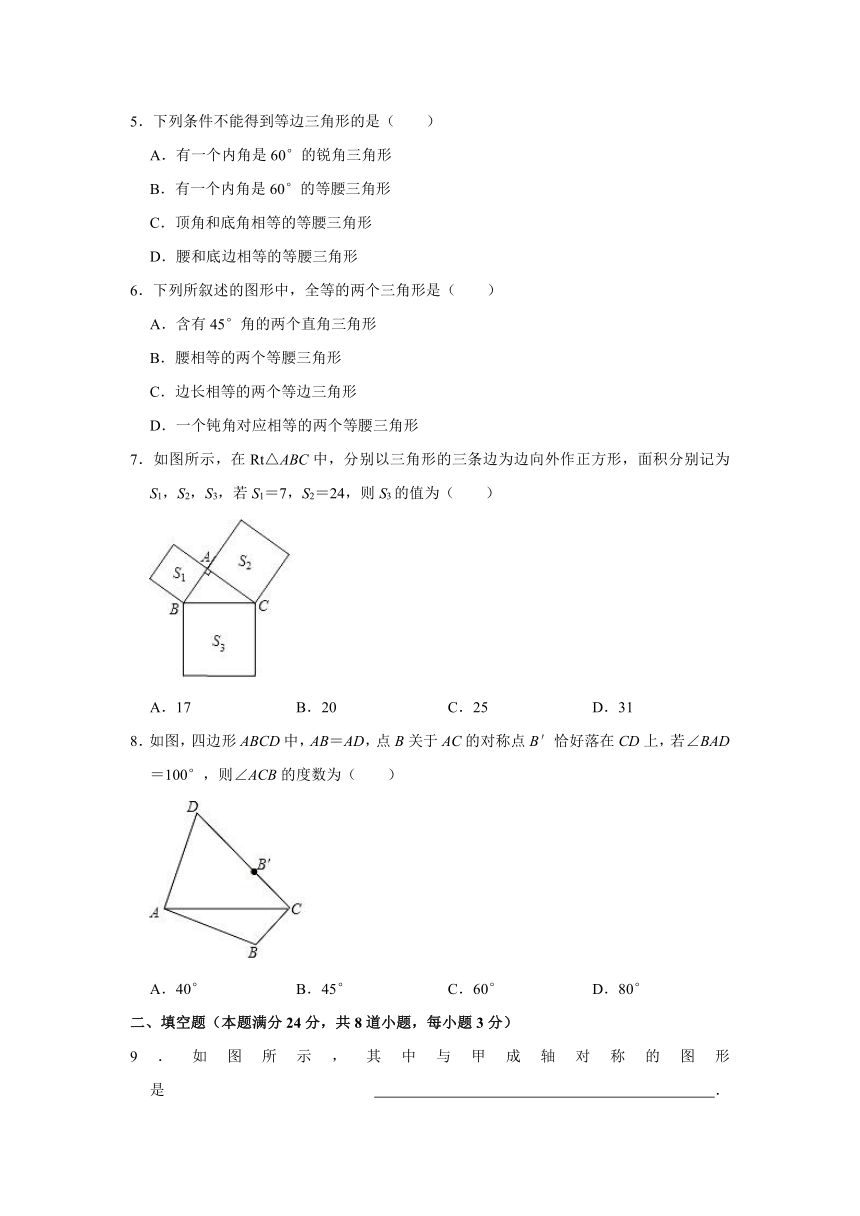
7.如图所示,在Rt△ABC中,分别以三角形的三条边为边向外作正方形,面积分别记为S1,S2,S3,若S1=7,S2=24,则S3的值为( )
A.17 B.20 C.25 D.31
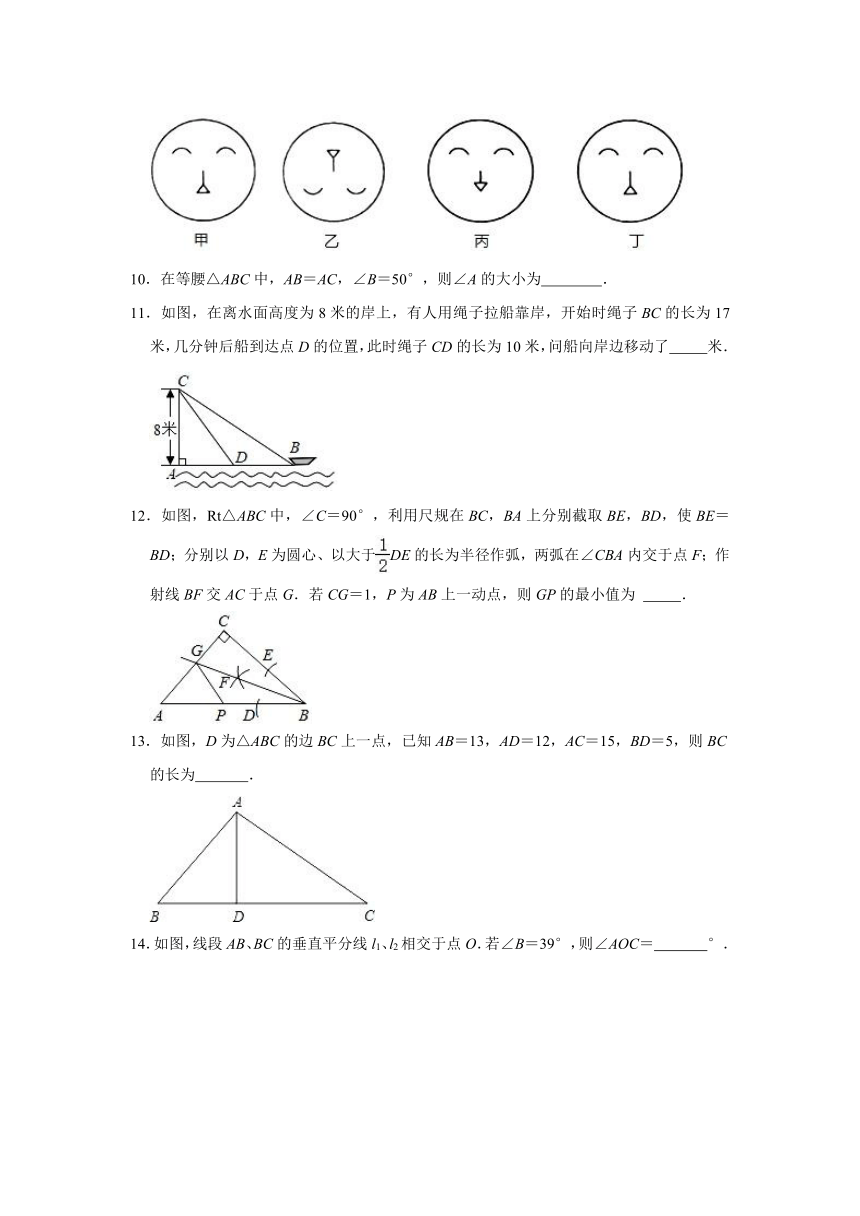
8.如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=100°,则∠ACB的度数为( )
A.40° B.45° C.60° D.80°
二、填空题(本题满分24分,共8道小题,每小题3分)
9.如图所示,其中与甲成轴对称的图形是 .
10.在等腰△ABC中,AB=AC,∠B=50°,则∠A的大小为 .
11.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了 米.
12.如图,Rt△ABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,BD,使BE=BD;分别以D,E为圆心、以大于DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为 .
13.如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为 .
14.如图,线段AB、BC的垂直平分线l1、l2相交于点O.若∠B=39°,则∠AOC= °.
15.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于E,若AC=5,则BD= .
16.如图,已知长方体的长AC=2cm,宽BC=1cm,高AA′=4cm.一只蚂蚁如果沿长方体的表面从A点爬到B′点,最短路程是 cm.
三.尺规作图(本题满分4分)用圆规、直尺作图,不写作法,但保留作图痕迹
17.已知:线段a,b和∠β.
求作:△ABC,使BC=a,AC=b,∠C=∠β.
四、解答题(本题满分68分,共7道小题)
18.如图,已知AD∥BC,BD是∠ABC的平分线,那么△ABD是等腰三角形吗?为什么?
19.如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm,求BC的长.
20.如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.
求证:△BED≌△CFD.
21.一船在灯塔C正东方向4海里的A处,以30海里/时的速度沿西偏北60°方向航行,求多长时间船到达灯塔的正北方?
22.两个大小不同的等腰直角三角形三角板如图1所示位置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连接DC.
(1)请找出图2中的全等三角形,并说明理由(说明:结论中不得有未标识的字母);
(2)判断DC⊥BE是否成立?说明理由.
23.某校七年级一班学生到野外活动,为测量一池塘两端A、B之间的距离,设计出如下几种方案:
方案a:如图(1)所示,先在平地上取一个可直接到达A、B的点C,再连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB之长;
方案b:如图(2)所示,过点B作AB的垂线BF,再在BF上取C、D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,则测出了DE的长即为A、B之间的距离.
阅读后回答下列问题:
(1)方案a是否可行?请说明理由.
(2)方案b是否可行?不必说明理由.
(3)方案b中作BF⊥AB,ED⊥BF的目的是 ,若仅满足∠ABD=∠BDE,方案b的结论是否成立
24.如图,在长方形ABCD中AB=DC=4,AD=BC=5,延长BC到E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒,存在这样的t,使△DCP和△DCE全等,则t的值为多少?
参考答案
一、选择题(本题满分24分,共8道小题,每小题3分)
1.下面图形中,是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:A.不是轴对称图形,故本选项不合题意;
B.不是轴对称图形,故本选项不合题意;
C.是轴对称图形,故本选项符合题意;
D.不是轴对称图形,故本选项不合题意.
故选:C.
2.下列四个选项中,不是全等图形的是( )
A.
B.
C.
D.
【分析】根据全等图形的概念判断即可.
解:A、两个图形是全等图形,不符合题意;
B、两个是全等图形,不符合题意;
C、两个图形大小不同,不是全等图形,符合题意;
D、两个图形是全等图形,不符合题意;
故选:C.
3.下列三角形是直角三角形的是( )
A. B.
C. D.
【分析】根据勾股定理的逆定理进行分析,从而不难得到答案..
解:由勾股定理的逆定理得,因为D能满足()2+()2=(2)2,所以D是直角三角形.
故选:D.
4.一个三角形的两边长分别为3和8,则它的第三边长可能是( )
A.5 B.12 C.10 D.无法确定
【分析】根据三角形三边关系:任意两边之和大于第三边以及任意两边之差小于第三边,即可得出第三边的取值范围.
解:∵此三角形的两边长分别为3和8,
∴第三边长的取值范围是:8﹣3<第三边<8+3.
即5<第三边<11,
观察选项,只有选项C符合题意.
故选:C.
5.下列条件不能得到等边三角形的是( )
A.有一个内角是60°的锐角三角形
B.有一个内角是60°的等腰三角形
C.顶角和底角相等的等腰三角形
D.腰和底边相等的等腰三角形
【分析】根据等边三角形的判定、等腰三角形的性质进行逐一判断即可.
解:因为有一个内角是60°的等腰三角形是等边三角形,
所以A选项符合题意;
所以B选项不符合题意;
因为顶角和底角相等的等腰三角形是等边三角形,
所以C不符合题意;
因为腰和底边相等的等腰三角形是等边三角形,
所以D选项不符合题意.
故选:A.
6.下列所叙述的图形中,全等的两个三角形是( )
A.含有45°角的两个直角三角形
B.腰相等的两个等腰三角形
C.边长相等的两个等边三角形
D.一个钝角对应相等的两个等腰三角形
【分析】根据全等三角形的判定解答即可.
解:A、含有45°角的两个直角三角形,没有指明边相等,所以不一定全等,选项不符合题意;
B、腰相等的两个等腰三角形,没有指明角相等,所以不一定全等,选项不符合题意;
C、边长相等的两个等边三角形,利用SSS可得一定全等,选项符合题意;
D、一个钝角对应相等的两个等腰三角形,没有指明边相等,所以不一定全等,选项不符合题意;
故选:C.
7.如图所示,在Rt△ABC中,分别以三角形的三条边为边向外作正方形,面积分别记为S1,S2,S3,若S1=7,S2=24,则S3的值为( )
A.17 B.20 C.25 D.31
【分析】由正方形的面积公式可知S1=AB2,S2=AC2,S3=BC2,在Rt△ABC中,由勾股定理得AC2+AB2=BC2,即S1+S2=S3,由此可求S3.
解:在Rt△ABC中,AC2+AB2=BC2,
由正方形面积公式得S1=AB2,S2=AC2,S3=BC2,
∵S1=9,S2=16,
∴S3=S1+S2=7+24=31.
故选:D.
8.如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=100°,则∠ACB的度数为( )
A.40° B.45° C.60° D.80°
【分析】连接AB',BB',过A作AE⊥CD于E,依据∠BAC=∠B'AC,∠DAE=∠B'AE,即可得出∠CAE=∠BAD,再根据四边形内角和以及三角形外角性质,即可得到∠ACB=∠ACB'=90°﹣∠BAD.
解:如图,连接AB',BB',过A作AE⊥CD于E,
∵点B关于AC的对称点B'恰好落在CD上,
∴AC垂直平分BB',
∴AB=AB',
∴∠BAC=∠B'AC,
∵AB=AD,
∴AD=AB',
又∵AE⊥CD,
∴∠DAE=∠B'AE,
∴∠CAE=∠BAD=50°,
又∵∠AEC=90°,
∴∠ACB=∠ACB'=40°,
故选:A.
二、填空题(本题满分24分,共8道小题,每小题3分)
9.如图所示,其中与甲成轴对称的图形是 丁 .
【分析】根据轴对称图形的概念对各选项分析判断即可得解.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:与甲成轴对称的图形是丁.
故答案为:丁.
10.在等腰△ABC中,AB=AC,∠B=50°,则∠A的大小为 80° .
【分析】根据等腰三角形两底角相等可求∠C,再根据三角形内角和为180°列式进行计算即可得解.
解:∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∴∠A=180°﹣2×50°=80°.
故答案为:80°.
11.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了 9 米.
【分析】在Rt△ABC中,利用勾股定理计算出AB长,再根据题意可得CD长,然后再次利用勾股定理计算出AD长,再利用BD=AB﹣AD可得BD长.
解:在Rt△ABC中:
∵∠CAB=90°,BC=17米,AC=8米,
∴AB===15(米),
∵CD=10(米),
∴AD==6(米),
∴BD=AB﹣AD=15﹣6=9(米),
答:船向岸边移动了9米,
故答案为:9.
12.如图,Rt△ABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,BD,使BE=BD;分别以D,E为圆心、以大于DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为 1 .
【分析】如图,过点G作GH⊥AB于H.根据角平分线的性质定理证明GH=GC=1,利用垂线段最短即可解决问题.
解:如图,过点G作GH⊥AB于H.
由作图可知,GB平分∠ABC,
∵GH⊥BA,GC⊥BC,
∴GH=GC=1,
根据垂线段最短可知,GP的最小值为1,
故答案为:1.
13.如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为 14 .
【分析】∵AD2+BD2=AB2∴AD⊥BC(勾股定理逆定理),在直角△ADC中,已知AD,AC即可求得CD,则BC=BD+DC.
解:∵AD2+BD2=144+25=169,
AB2=169,∴AD2+BD2=AB2
∴AD⊥BC(勾股定理逆定理),
∠ADC=90°,
∴CD===9,
∴BC=CD+BD=5+9=14.
故答案为14.
14.如图,线段AB、BC的垂直平分线l1、l2相交于点O.若∠B=39°,则∠AOC= 78 °.
【分析】连接BO并延长至D,根据线段垂直平分线的性质得到OA=OB,OC=OB,根据等腰三角形的性质、三角形的外角性质计算,得到答案.
解:连接BO并延长至D,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴OA=OB,OC=OB,
∴∠OAB=∠OBA,∠OCB=∠OBC,
∴∠AOD=2∠OBA,∠COD=2∠OBC,
∴∠AOC=2(∠OBA+∠OBC)=2∠ABC=78°,
故答案为:78.
15.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于E,若AC=5,则BD= 10 .
【分析】如图,连接AD.根据线段垂直平分线的性质将BD的长度转化为AD的长度,所以在直角△ACD中,利用含30度角的直角三角形来求AD的长度.
解:如图,连接AD.
∵AB的垂直平分线交BC于D,
∴AD=BD,
∴∠BAD=∠B=15°,
∴∠ADC=∠BAD+∠B=30°.
又∵在△ABC中,∠C=90°,AC=5,
∴AD=2AC=10.
故填:10.
16.如图,已知长方体的长AC=2cm,宽BC=1cm,高AA′=4cm.一只蚂蚁如果沿长方体的表面从A点爬到B′点,最短路程是 5 cm.
【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
解:根据题意,如图所示,最短路径有以下三种情况:
(1)沿AA′,A′C′,C′B′,B′B剪开,得图1:
AB′2=AB2+BB′2=(2+1)2+42=25;
(2)沿AC,CC′,C′B′,B′D′,D′A′,A′A剪开,得图2:
AB′2=AC2+B′C2=22+(4+1)2=4+25=29;
(3)沿AD,DD′,B′D′,C′B′,C′A′,AA′剪开,得图3:
AB′2=AD2+B′D2=12+(4+2)2=1+36=37;
综上所述,最短路径应为(1)所示,所以AB′2=25,即AB′=5cm,
故答案为:5.
三.尺规作图(本题满分4分)用圆规、直尺作图,不写作法,但保留作图痕迹
17.已知:线段a,b和∠β.
求作:△ABC,使BC=a,AC=b,∠C=∠β.
【分析】作∠MCN=∠β,分别在射线CM,CN上截取CB,CA,使得CB=a,CA=b,连接AB,△ABC即为所求.
解:如图,△ABC即为所求.
四、解答题(本题满分68分,共7道小题)
18.如图,已知AD∥BC,BD是∠ABC的平分线,那么△ABD是等腰三角形吗?为什么?
【分析】根据BD是∠ABC的平分线得到∠ABD=∠DBC,然后利用平行线性质得到∠ADB=∠DBC,从而∠ADB=∠ABD,进而证得△ABD是等腰三角形.
解:△ABD是等腰三角形,
理由是:
∵BD是∠ABC的平分线
∴∠ABD=∠DBC
又∵AD∥BC
∴∠ADB=∠DBC(两直线平等,内错角相等)
∴∠ADB=∠ABD
∴△ABD是等腰三角形.
19.如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm,求BC的长.
【分析】根据等腰三角形性质求出∠B,求出∠BAC,求出∠DAC=∠C,求出AD=DC=4cm,根据含30度角的直角三角形性质求出BD,即可求出答案.
解:∵AB=AC,∠C=30°,
∴∠B=30°,
∵AB⊥AD,AD=4cm,
∴BD=8cm,
∵∠ADB=60°,∠C=30°,
∴∠DAC=∠C=30°,
∴CD=AD=4cm,
∴BC=BD+CD=8+4=12cm.
20.如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.
求证:△BED≌△CFD.
【分析】首先根据AB=AC可得∠B=∠C,再由DE⊥AB,DF⊥AC,可得∠BED=∠CFD=90°,然后再利用AAS定理可判定△BED≌△CFD.
【解答】证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵AB=AC,
∴∠B=∠C,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS).
21.一船在灯塔C正东方向4海里的A处,以30海里/时的速度沿西偏北60°方向航行,求多长时间船到达灯塔的正北方?
【分析】画出图形,由题意得∠A=60°,当船到达灯塔的正北B点时,∠BCA=90°,则∠B=30°,再由含30°角的直角三角形的性质得AB=2AC=8(海里),即可求解.
解:如图,由题意得∠A=60°,AC=4海里,
当船到达灯塔的正北B点时,∠BCA=90°,
∴∠B=30°
∴AB=2AC=2×4=8(海里),
∴8÷30=(小时)=16分钟,
答:16分钟后,船到达灯塔的正北方.
22.两个大小不同的等腰直角三角形三角板如图1所示位置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连接DC.
(1)请找出图2中的全等三角形,并说明理由(说明:结论中不得有未标识的字母);
(2)判断DC⊥BE是否成立?说明理由.
【分析】(1)根据等腰直角三角形的性质可以得出△ABE≌△ACD;
(2)由△ABE≌△ACD可以得出∠AEB=∠ADC,进而得出∠AEC=90°,就可以得出结论.
解:(1)结论:△ABE≌△ACD.
理由:∵△ABC和△ADE是等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°,
∴∠BAC+∠EAC=∠DAE+∠EAC,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS).
(2)∵△ABE≌△ACD,
∴∠AEB=∠ADC.
∵∠ADC+∠AFD=90°,
∴∠AEB+∠AFD=90°.
∵∠AFD=∠CFE,
∴∠AEB+∠CFE=90°,
∴∠FCE=90°,
∴DC⊥BE.
23.某校七年级一班学生到野外活动,为测量一池塘两端A、B之间的距离,设计出如下几种方案:
方案a:如图(1)所示,先在平地上取一个可直接到达A、B的点C,再连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB之长;
方案b:如图(2)所示,过点B作AB的垂线BF,再在BF上取C、D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,则测出了DE的长即为A、B之间的距离.
阅读后回答下列问题:
(1)方案a是否可行?请说明理由.
(2)方案b是否可行?不必说明理由.
(3)方案b中作BF⊥AB,ED⊥BF的目的是 对应角∠ABD=∠BDE=90° ,若仅满足∠ABD=∠BDE,方案b的结论是否成立
【分析】(1)方案a对顶角相等,只要夹这个角的两边相等,利用“边角边”就可以判断三角形全等.
(2)方案b对顶角相等,又有垂直,两个对应角是直角,利用“角边角”,就可以判断两个三角形全等;
(3)根据垂直的定义即可得到结论.
解:(1)可行,
理由:由边角边说明△ACB≌△DCE,则DE=AB.
(2)可行,
理由:由角边角说明△ABC≌△EDC,则DE=AB.
(3)作BF⊥AB,ED⊥BF的目的是对应角∠ABD=∠BDE=90°,只要∠ABC=∠BDE,方案b仍成立.
故答案为:对应角∠ABD=∠BDE=90°.
24.如图,在长方形ABCD中AB=DC=4,AD=BC=5,延长BC到E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒,存在这样的t,使△DCP和△DCE全等,则t的值为多少?
【分析】分两种情况进行讨论,根据题意列方程即可求得.
解:①当P在BC上时,由题意得BP=2t,
∵∠DCP=∠DCE=90°,CD为公共边,
∴要使△DCP≌△DCE,则需CP=CE,如图1所示:
∵CE=2,
∴5﹣2t=2,
∴,
即当时,△DCP≌△DCE;
②当P在AD上时,由题意得BC+CD+DP=2t,
∵BC=5,CD=4,
∴DP=2t﹣9,
∵∠CDP=∠DCE=90°,CD为公共边,
∴要使△DCP≌△CDE,则需DP=CE,如图2所示:
即2t﹣9=2,
∴,
即当时,△DCP≌△CDE,
∴当或时,△DCP和△DCE全等.
一、选择题(本题满分24分,共8道小题,每小题3分)
1.下面图形中,是轴对称图形的是( )
A. B. C. D.
2.下列四个选项中,不是全等图形的是( )
A.
B.
C.
D.
3.下列三角形是直角三角形的是( )
A. B.
C. D.
4.一个三角形的两边长分别为3和8,则它的第三边长可能是( )
A.5 B.12 C.10 D.无法确定
5.下列条件不能得到等边三角形的是( )
A.有一个内角是60°的锐角三角形
B.有一个内角是60°的等腰三角形
C.顶角和底角相等的等腰三角形
D.腰和底边相等的等腰三角形
6.下列所叙述的图形中,全等的两个三角形是( )
A.含有45°角的两个直角三角形
B.腰相等的两个等腰三角形
C.边长相等的两个等边三角形
D.一个钝角对应相等的两个等腰三角形
7.如图所示,在Rt△ABC中,分别以三角形的三条边为边向外作正方形,面积分别记为S1,S2,S3,若S1=7,S2=24,则S3的值为( )
A.17 B.20 C.25 D.31
8.如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=100°,则∠ACB的度数为( )
A.40° B.45° C.60° D.80°
二、填空题(本题满分24分,共8道小题,每小题3分)
9.如图所示,其中与甲成轴对称的图形是 .
10.在等腰△ABC中,AB=AC,∠B=50°,则∠A的大小为 .
11.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了 米.
12.如图,Rt△ABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,BD,使BE=BD;分别以D,E为圆心、以大于DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为 .
13.如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为 .
14.如图,线段AB、BC的垂直平分线l1、l2相交于点O.若∠B=39°,则∠AOC= °.
15.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于E,若AC=5,则BD= .
16.如图,已知长方体的长AC=2cm,宽BC=1cm,高AA′=4cm.一只蚂蚁如果沿长方体的表面从A点爬到B′点,最短路程是 cm.
三.尺规作图(本题满分4分)用圆规、直尺作图,不写作法,但保留作图痕迹
17.已知:线段a,b和∠β.
求作:△ABC,使BC=a,AC=b,∠C=∠β.
四、解答题(本题满分68分,共7道小题)
18.如图,已知AD∥BC,BD是∠ABC的平分线,那么△ABD是等腰三角形吗?为什么?
19.如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm,求BC的长.
20.如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.
求证:△BED≌△CFD.
21.一船在灯塔C正东方向4海里的A处,以30海里/时的速度沿西偏北60°方向航行,求多长时间船到达灯塔的正北方?
22.两个大小不同的等腰直角三角形三角板如图1所示位置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连接DC.
(1)请找出图2中的全等三角形,并说明理由(说明:结论中不得有未标识的字母);
(2)判断DC⊥BE是否成立?说明理由.
23.某校七年级一班学生到野外活动,为测量一池塘两端A、B之间的距离,设计出如下几种方案:
方案a:如图(1)所示,先在平地上取一个可直接到达A、B的点C,再连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB之长;
方案b:如图(2)所示,过点B作AB的垂线BF,再在BF上取C、D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,则测出了DE的长即为A、B之间的距离.
阅读后回答下列问题:
(1)方案a是否可行?请说明理由.
(2)方案b是否可行?不必说明理由.
(3)方案b中作BF⊥AB,ED⊥BF的目的是 ,若仅满足∠ABD=∠BDE,方案b的结论是否成立
24.如图,在长方形ABCD中AB=DC=4,AD=BC=5,延长BC到E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒,存在这样的t,使△DCP和△DCE全等,则t的值为多少?
参考答案
一、选择题(本题满分24分,共8道小题,每小题3分)
1.下面图形中,是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:A.不是轴对称图形,故本选项不合题意;
B.不是轴对称图形,故本选项不合题意;
C.是轴对称图形,故本选项符合题意;
D.不是轴对称图形,故本选项不合题意.
故选:C.
2.下列四个选项中,不是全等图形的是( )
A.
B.
C.
D.
【分析】根据全等图形的概念判断即可.
解:A、两个图形是全等图形,不符合题意;
B、两个是全等图形,不符合题意;
C、两个图形大小不同,不是全等图形,符合题意;
D、两个图形是全等图形,不符合题意;
故选:C.
3.下列三角形是直角三角形的是( )
A. B.
C. D.
【分析】根据勾股定理的逆定理进行分析,从而不难得到答案..
解:由勾股定理的逆定理得,因为D能满足()2+()2=(2)2,所以D是直角三角形.
故选:D.
4.一个三角形的两边长分别为3和8,则它的第三边长可能是( )
A.5 B.12 C.10 D.无法确定
【分析】根据三角形三边关系:任意两边之和大于第三边以及任意两边之差小于第三边,即可得出第三边的取值范围.
解:∵此三角形的两边长分别为3和8,
∴第三边长的取值范围是:8﹣3<第三边<8+3.
即5<第三边<11,
观察选项,只有选项C符合题意.
故选:C.
5.下列条件不能得到等边三角形的是( )
A.有一个内角是60°的锐角三角形
B.有一个内角是60°的等腰三角形
C.顶角和底角相等的等腰三角形
D.腰和底边相等的等腰三角形
【分析】根据等边三角形的判定、等腰三角形的性质进行逐一判断即可.
解:因为有一个内角是60°的等腰三角形是等边三角形,
所以A选项符合题意;
所以B选项不符合题意;
因为顶角和底角相等的等腰三角形是等边三角形,
所以C不符合题意;
因为腰和底边相等的等腰三角形是等边三角形,
所以D选项不符合题意.
故选:A.
6.下列所叙述的图形中,全等的两个三角形是( )
A.含有45°角的两个直角三角形
B.腰相等的两个等腰三角形
C.边长相等的两个等边三角形
D.一个钝角对应相等的两个等腰三角形
【分析】根据全等三角形的判定解答即可.
解:A、含有45°角的两个直角三角形,没有指明边相等,所以不一定全等,选项不符合题意;
B、腰相等的两个等腰三角形,没有指明角相等,所以不一定全等,选项不符合题意;
C、边长相等的两个等边三角形,利用SSS可得一定全等,选项符合题意;
D、一个钝角对应相等的两个等腰三角形,没有指明边相等,所以不一定全等,选项不符合题意;
故选:C.
7.如图所示,在Rt△ABC中,分别以三角形的三条边为边向外作正方形,面积分别记为S1,S2,S3,若S1=7,S2=24,则S3的值为( )
A.17 B.20 C.25 D.31
【分析】由正方形的面积公式可知S1=AB2,S2=AC2,S3=BC2,在Rt△ABC中,由勾股定理得AC2+AB2=BC2,即S1+S2=S3,由此可求S3.
解:在Rt△ABC中,AC2+AB2=BC2,
由正方形面积公式得S1=AB2,S2=AC2,S3=BC2,
∵S1=9,S2=16,
∴S3=S1+S2=7+24=31.
故选:D.
8.如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=100°,则∠ACB的度数为( )
A.40° B.45° C.60° D.80°
【分析】连接AB',BB',过A作AE⊥CD于E,依据∠BAC=∠B'AC,∠DAE=∠B'AE,即可得出∠CAE=∠BAD,再根据四边形内角和以及三角形外角性质,即可得到∠ACB=∠ACB'=90°﹣∠BAD.
解:如图,连接AB',BB',过A作AE⊥CD于E,
∵点B关于AC的对称点B'恰好落在CD上,
∴AC垂直平分BB',
∴AB=AB',
∴∠BAC=∠B'AC,
∵AB=AD,
∴AD=AB',
又∵AE⊥CD,
∴∠DAE=∠B'AE,
∴∠CAE=∠BAD=50°,
又∵∠AEC=90°,
∴∠ACB=∠ACB'=40°,
故选:A.
二、填空题(本题满分24分,共8道小题,每小题3分)
9.如图所示,其中与甲成轴对称的图形是 丁 .
【分析】根据轴对称图形的概念对各选项分析判断即可得解.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:与甲成轴对称的图形是丁.
故答案为:丁.
10.在等腰△ABC中,AB=AC,∠B=50°,则∠A的大小为 80° .
【分析】根据等腰三角形两底角相等可求∠C,再根据三角形内角和为180°列式进行计算即可得解.
解:∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∴∠A=180°﹣2×50°=80°.
故答案为:80°.
11.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了 9 米.
【分析】在Rt△ABC中,利用勾股定理计算出AB长,再根据题意可得CD长,然后再次利用勾股定理计算出AD长,再利用BD=AB﹣AD可得BD长.
解:在Rt△ABC中:
∵∠CAB=90°,BC=17米,AC=8米,
∴AB===15(米),
∵CD=10(米),
∴AD==6(米),
∴BD=AB﹣AD=15﹣6=9(米),
答:船向岸边移动了9米,
故答案为:9.
12.如图,Rt△ABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,BD,使BE=BD;分别以D,E为圆心、以大于DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为 1 .
【分析】如图,过点G作GH⊥AB于H.根据角平分线的性质定理证明GH=GC=1,利用垂线段最短即可解决问题.
解:如图,过点G作GH⊥AB于H.
由作图可知,GB平分∠ABC,
∵GH⊥BA,GC⊥BC,
∴GH=GC=1,
根据垂线段最短可知,GP的最小值为1,
故答案为:1.
13.如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为 14 .
【分析】∵AD2+BD2=AB2∴AD⊥BC(勾股定理逆定理),在直角△ADC中,已知AD,AC即可求得CD,则BC=BD+DC.
解:∵AD2+BD2=144+25=169,
AB2=169,∴AD2+BD2=AB2
∴AD⊥BC(勾股定理逆定理),
∠ADC=90°,
∴CD===9,
∴BC=CD+BD=5+9=14.
故答案为14.
14.如图,线段AB、BC的垂直平分线l1、l2相交于点O.若∠B=39°,则∠AOC= 78 °.
【分析】连接BO并延长至D,根据线段垂直平分线的性质得到OA=OB,OC=OB,根据等腰三角形的性质、三角形的外角性质计算,得到答案.
解:连接BO并延长至D,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴OA=OB,OC=OB,
∴∠OAB=∠OBA,∠OCB=∠OBC,
∴∠AOD=2∠OBA,∠COD=2∠OBC,
∴∠AOC=2(∠OBA+∠OBC)=2∠ABC=78°,
故答案为:78.
15.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于E,若AC=5,则BD= 10 .
【分析】如图,连接AD.根据线段垂直平分线的性质将BD的长度转化为AD的长度,所以在直角△ACD中,利用含30度角的直角三角形来求AD的长度.
解:如图,连接AD.
∵AB的垂直平分线交BC于D,
∴AD=BD,
∴∠BAD=∠B=15°,
∴∠ADC=∠BAD+∠B=30°.
又∵在△ABC中,∠C=90°,AC=5,
∴AD=2AC=10.
故填:10.
16.如图,已知长方体的长AC=2cm,宽BC=1cm,高AA′=4cm.一只蚂蚁如果沿长方体的表面从A点爬到B′点,最短路程是 5 cm.
【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
解:根据题意,如图所示,最短路径有以下三种情况:
(1)沿AA′,A′C′,C′B′,B′B剪开,得图1:
AB′2=AB2+BB′2=(2+1)2+42=25;
(2)沿AC,CC′,C′B′,B′D′,D′A′,A′A剪开,得图2:
AB′2=AC2+B′C2=22+(4+1)2=4+25=29;
(3)沿AD,DD′,B′D′,C′B′,C′A′,AA′剪开,得图3:
AB′2=AD2+B′D2=12+(4+2)2=1+36=37;
综上所述,最短路径应为(1)所示,所以AB′2=25,即AB′=5cm,
故答案为:5.
三.尺规作图(本题满分4分)用圆规、直尺作图,不写作法,但保留作图痕迹
17.已知:线段a,b和∠β.
求作:△ABC,使BC=a,AC=b,∠C=∠β.
【分析】作∠MCN=∠β,分别在射线CM,CN上截取CB,CA,使得CB=a,CA=b,连接AB,△ABC即为所求.
解:如图,△ABC即为所求.
四、解答题(本题满分68分,共7道小题)
18.如图,已知AD∥BC,BD是∠ABC的平分线,那么△ABD是等腰三角形吗?为什么?
【分析】根据BD是∠ABC的平分线得到∠ABD=∠DBC,然后利用平行线性质得到∠ADB=∠DBC,从而∠ADB=∠ABD,进而证得△ABD是等腰三角形.
解:△ABD是等腰三角形,
理由是:
∵BD是∠ABC的平分线
∴∠ABD=∠DBC
又∵AD∥BC
∴∠ADB=∠DBC(两直线平等,内错角相等)
∴∠ADB=∠ABD
∴△ABD是等腰三角形.
19.如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm,求BC的长.
【分析】根据等腰三角形性质求出∠B,求出∠BAC,求出∠DAC=∠C,求出AD=DC=4cm,根据含30度角的直角三角形性质求出BD,即可求出答案.
解:∵AB=AC,∠C=30°,
∴∠B=30°,
∵AB⊥AD,AD=4cm,
∴BD=8cm,
∵∠ADB=60°,∠C=30°,
∴∠DAC=∠C=30°,
∴CD=AD=4cm,
∴BC=BD+CD=8+4=12cm.
20.如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.
求证:△BED≌△CFD.
【分析】首先根据AB=AC可得∠B=∠C,再由DE⊥AB,DF⊥AC,可得∠BED=∠CFD=90°,然后再利用AAS定理可判定△BED≌△CFD.
【解答】证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵AB=AC,
∴∠B=∠C,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS).
21.一船在灯塔C正东方向4海里的A处,以30海里/时的速度沿西偏北60°方向航行,求多长时间船到达灯塔的正北方?
【分析】画出图形,由题意得∠A=60°,当船到达灯塔的正北B点时,∠BCA=90°,则∠B=30°,再由含30°角的直角三角形的性质得AB=2AC=8(海里),即可求解.
解:如图,由题意得∠A=60°,AC=4海里,
当船到达灯塔的正北B点时,∠BCA=90°,
∴∠B=30°
∴AB=2AC=2×4=8(海里),
∴8÷30=(小时)=16分钟,
答:16分钟后,船到达灯塔的正北方.
22.两个大小不同的等腰直角三角形三角板如图1所示位置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连接DC.
(1)请找出图2中的全等三角形,并说明理由(说明:结论中不得有未标识的字母);
(2)判断DC⊥BE是否成立?说明理由.
【分析】(1)根据等腰直角三角形的性质可以得出△ABE≌△ACD;
(2)由△ABE≌△ACD可以得出∠AEB=∠ADC,进而得出∠AEC=90°,就可以得出结论.
解:(1)结论:△ABE≌△ACD.
理由:∵△ABC和△ADE是等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°,
∴∠BAC+∠EAC=∠DAE+∠EAC,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS).
(2)∵△ABE≌△ACD,
∴∠AEB=∠ADC.
∵∠ADC+∠AFD=90°,
∴∠AEB+∠AFD=90°.
∵∠AFD=∠CFE,
∴∠AEB+∠CFE=90°,
∴∠FCE=90°,
∴DC⊥BE.
23.某校七年级一班学生到野外活动,为测量一池塘两端A、B之间的距离,设计出如下几种方案:
方案a:如图(1)所示,先在平地上取一个可直接到达A、B的点C,再连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB之长;
方案b:如图(2)所示,过点B作AB的垂线BF,再在BF上取C、D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,则测出了DE的长即为A、B之间的距离.
阅读后回答下列问题:
(1)方案a是否可行?请说明理由.
(2)方案b是否可行?不必说明理由.
(3)方案b中作BF⊥AB,ED⊥BF的目的是 对应角∠ABD=∠BDE=90° ,若仅满足∠ABD=∠BDE,方案b的结论是否成立
【分析】(1)方案a对顶角相等,只要夹这个角的两边相等,利用“边角边”就可以判断三角形全等.
(2)方案b对顶角相等,又有垂直,两个对应角是直角,利用“角边角”,就可以判断两个三角形全等;
(3)根据垂直的定义即可得到结论.
解:(1)可行,
理由:由边角边说明△ACB≌△DCE,则DE=AB.
(2)可行,
理由:由角边角说明△ABC≌△EDC,则DE=AB.
(3)作BF⊥AB,ED⊥BF的目的是对应角∠ABD=∠BDE=90°,只要∠ABC=∠BDE,方案b仍成立.
故答案为:对应角∠ABD=∠BDE=90°.
24.如图,在长方形ABCD中AB=DC=4,AD=BC=5,延长BC到E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒,存在这样的t,使△DCP和△DCE全等,则t的值为多少?
【分析】分两种情况进行讨论,根据题意列方程即可求得.
解:①当P在BC上时,由题意得BP=2t,
∵∠DCP=∠DCE=90°,CD为公共边,
∴要使△DCP≌△DCE,则需CP=CE,如图1所示:
∵CE=2,
∴5﹣2t=2,
∴,
即当时,△DCP≌△DCE;
②当P在AD上时,由题意得BC+CD+DP=2t,
∵BC=5,CD=4,
∴DP=2t﹣9,
∵∠CDP=∠DCE=90°,CD为公共边,
∴要使△DCP≌△CDE,则需DP=CE,如图2所示:
即2t﹣9=2,
∴,
即当时,△DCP≌△CDE,
∴当或时,△DCP和△DCE全等.
同课章节目录
