因式分解单元复习
图片预览











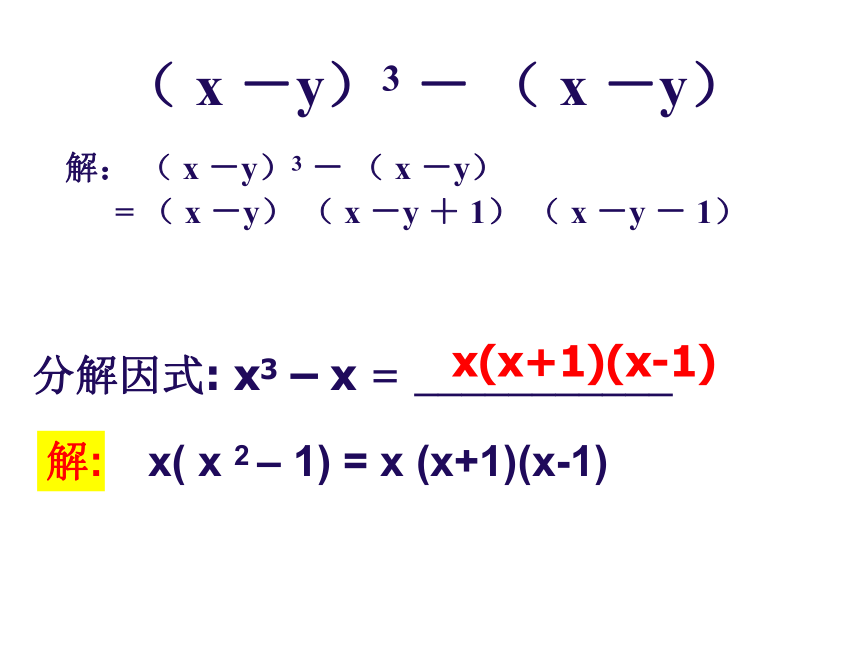
文档简介
(共30张PPT)
把一个多项式化成几个整式的积的形式叫做因式分解,也叫分解因式。
(一)因式分解的定义:
基本概念
即:一个多项式 →几个整式的积
练习题:
一个多项式分解因式的结果为(x+3)(x+4),则这个多项式为( )
x2 +7 x +12
(二)因式分解的方法:
(1)、提取公因式法
(2)、运用公式法
如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成乘积的形式。这种分解因式的方法叫做提取公因式。
练习题: 分解因式
2.p(y-x)-q(y-x)
(1)、提取公因式法:
解: p(y-x)-q(y-x)
= (y-x)( p -q)
即: ma + mb + mc = m(a+b+c)
1 . X2 – 9= ______
(x+3)(x-3)
1.公因式确定
(1)系数:取各系数的最大公约数;
(2)字母:取各项相同的字母;
(3)相同字母的指数:取最低指数。
2.变形规律:
(1)x-y=-(y-x) (2) -x-y=-(x+y)
(3) (x-y)2=(y-x)2 (4) (x-y)3=-(y-x)3
3.一般步骤
(1)确定应提取的公因式;
(2)多项式除以公因式,所得的商作为另一个因式;
(3)把多项式写成这两个因式的积的形式。
提公因式法:
练习题:
.分解因式: ax2y+axy2
=axy(x+y)
(2)运用公式法:
如果把乘法公式反过来应用,就可以把多项式写成积的形式,达到分解因式目的。这种方法叫做公式法。
① a2-b2=(a+b)(a-b) [ 平方差公式 ] 练习
② a2 +2ab+ b2 =(a+b)2 [ 完全平方和公式 ] 练习
a2 -2ab- b2 =(a-b)2 [ 完全平方差公式 ]
公式法中主要使用的公式有如下几个:
用平方差公式分解因式的关键:多项式是否能看成两个数的平方的差;
用完全平方公式分解因式的关键:在于判断一个多项式是否为一个完全平方式;
平方差公式:a2-b2=(a+b)(a-b)
完全平方公式:a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
公式法
练习题: 分解因式 x2-(2y)2
a2-b2=(a+b)(a-b) [ 平方差公式 ]
解: x2-(2y)2
=(x+2y)(x-2y)
练习题:
下列各式能用完全平方公式分解因式的是( )
A、x2+x+2y2 B、 x2 +4x-4
C、x2+4xy+y2 D、 y2 -4xy+4 x2
② a2 +2ab+ b2 =(a+b)2
a2 -2ab- b2 =(a-b)2
D
因式分解的一般步骤:
一提:先看多项式各项有无公因式,如有公因式则要先提取公因式;
二套:再看有几项,
如两项,则考虑用平方差公式;如三项,则考虑用完全平方公 式;
四查:最后用整式乘法检验一遍,并看各因式能否再分解,如能分解,应分解到不能再分解为止。
一般步骤
三变:若以上两步都不行,则将考虑将多项式变形,使之能“提”或能“套”。[如(x+y) -x-y=(x+y)(x+y-1)
第二步第二环节
1.分解因式:m2 – n2 + 2m - 2n (北京市)
解:
原式=(m2-n2) + (2m – 2n)
=( m + n )( m – n )+2( m – n )
=( m - n )( m + n +2)
2.分解因式: x3 – xy2 ( 沈阳市)
解:
原式= x ( x2 – y2 )
= x ( x + y )( x – y )
( x -y)3 - ( x -y)
解: ( x -y)3 - ( x -y)
= ( x -y) ( x -y + 1) ( x -y - 1)
分解因式: x3 – x = ___________
x( x 2 – 1) = x (x+1)(x-1)
解:
x(x+1)(x-1)
分解因式:(4x2+1)2 – 16x2
解:
(4x2+1)2 – 16x2
=(4x2+1+4x)(4x2+1-4x)
=(2x+1)2(2x-1)2
=(4x2+4x+1)(4x2-4x+1)
.将 x – xy2 分解因式______________
解:
x – xy2=x(1-y2)
=x(1+y)(1-y)
x(1+y)(1-y)
=[3(m+n)]2- (m-n)2
=[3(m+n)+ (m-n)][3(m+n)- (m-n)]
=(3m+3n+m-n)(3m+3n-m+n)
9(m+n)2-(m-n)2
=(4m+2n)(2m+4n)
=4(2m+n)(m+2n)
(广西)
简化计算
主要应用
多项式的除法
解方程
简化计算
(1)562+56×44 (2)1012 - 992
变式
若a=99,b=-1,则a2-2ab+b2=____________;
超级变变变
解方程:
x -9x=0
变式
解下列方程:
(3x- 4) - (3x+ 4) =48
多项式的除法
(2mp-3mq+4mr) ÷(2p-3q+4r)
变式:
20052+2005能被2006整除吗?
第三步
求证:对于自然数n,2n+4-2n能被30整除.
解:2n+4-2n=2n(24-1)=2n(16-1)=15×2n
=15×2×2n-1=30×2n-1.
∵n为自然数时,2n-1为整数,
∴2n+4-2n能被30整除.
典型例题解析
大
已知a、b、c是一个三角形的三边,判断代数式a2-b2 -c2 –2bc 的正负性。(提示: a2-b2 -c2 –2bc = a2-(b2+c2 +2bc )
比
一个矩形的面积为a3 -2ab+a ,宽为 a ,则矩形的长为_____________
( 安徽 )
解:
矩形的长=(a3-2ab+a)÷a
=a2 – 2b+1
a2 – 2b+1
(黄冈)
若a2-2a+1=0 , 2a2- 4a =_____
解法一:
由a2-2a+1=0得(a-1)2=0,∴a=1
∴ 2a2- 4a =2×12 - 4×1= -2
解法二:
由a2-2a+1=0得a2-2a=-1,
∴ 2a2- 4a =2(a2-2a)
=2×(-1)
=-2
解法三:
2a2- 4a= 2a2- 4a+2-2
=2(a2-2a+1)-2
=2×0-2=-2
-2
(广州)
如果 x2+x-1=0, 那么代数式 x3+2x2 -7的值为( )
x2+x-1=0得x2=1-x,
则x3+2x2-7=x(1-x)+2(1-x)-7
=x-x2+2-2x-7=-x2-x-5
=-(x2+x)-5=-(x2+x-1)-6
=-6
解:
A. 6 B. 8 C. -6 D. -8
C
(福州市)
(厦门市)
已知: a+b =m , ab = -4,
化简:(a-2)(b-2)的结果是( )
A. 6 ; B. 2m-8 ; C. 2m , D.-2m
D
(厦门市)
解:
(a-2)(b-2)
=ab-2a-2b+4
=ab-2(a+b)+4
=-4-2m+4
=-2m
已知 2n+2-n=k(n为正整数),
则4n+4-n=______(用含k的代数式示).
(烟台市)
K2 -2
解:
4n+4-n=(2n)2+(2-n)2
= (2n+2-n)2 -2n·2-n
= k2 - 2
在多项式4x2+1中添加一个单项式,使其成为一个完全平方式,则添加的单项式是________ (只写一个即可)
4x或 -4x
已知 a–b=b-c=3/5 , a2+b2+c2=1 ,ab+bc+ca=____
(宁波市)
解:
由已知得a+c=2b (1) ,a =3/5+b ,
∴(3/5+b)2+b2+(b-3/5 )2=1
c=b-3/5,
∵(a+b+c)2=a2+b2+c2+2ab+2bc+2ca
b2=7/75 ,
若 ( )
A. B. C. D.
(潍坊市)
解:
A
在日常生活中取款、上网等都需要密码,有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式 x4 – x4 , 因式分解的结果是(x –y)(x+y)(x2+y2), 若取x=9 ,y=9时,则各个因式的值是: (x-y)=0 , (x+y) =18 , (x2+y2) =162, 于是就可以把“018162”作为一个六位数的密码, 对于多项式 4x3 – xy2 , 取x =10 , y = 10 时, 用上述方法产生的密码是:___________________________
101030 ;
(写一个即可) (浙江)
或103010 ;
或301010
4x3 – xy2 = x (2x-y)(2x+y)
x=10 , 2x-y =10 , 2x+y =30
因式分解应进行到底.
如:分解因式:x4-4=(x2+2)(x2-2)
=(x2+2)(x+ )(x- ).
应在实数范围内将它分解到底.
把一个多项式化成几个整式的积的形式叫做因式分解,也叫分解因式。
(一)因式分解的定义:
基本概念
即:一个多项式 →几个整式的积
练习题:
一个多项式分解因式的结果为(x+3)(x+4),则这个多项式为( )
x2 +7 x +12
(二)因式分解的方法:
(1)、提取公因式法
(2)、运用公式法
如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成乘积的形式。这种分解因式的方法叫做提取公因式。
练习题: 分解因式
2.p(y-x)-q(y-x)
(1)、提取公因式法:
解: p(y-x)-q(y-x)
= (y-x)( p -q)
即: ma + mb + mc = m(a+b+c)
1 . X2 – 9= ______
(x+3)(x-3)
1.公因式确定
(1)系数:取各系数的最大公约数;
(2)字母:取各项相同的字母;
(3)相同字母的指数:取最低指数。
2.变形规律:
(1)x-y=-(y-x) (2) -x-y=-(x+y)
(3) (x-y)2=(y-x)2 (4) (x-y)3=-(y-x)3
3.一般步骤
(1)确定应提取的公因式;
(2)多项式除以公因式,所得的商作为另一个因式;
(3)把多项式写成这两个因式的积的形式。
提公因式法:
练习题:
.分解因式: ax2y+axy2
=axy(x+y)
(2)运用公式法:
如果把乘法公式反过来应用,就可以把多项式写成积的形式,达到分解因式目的。这种方法叫做公式法。
① a2-b2=(a+b)(a-b) [ 平方差公式 ] 练习
② a2 +2ab+ b2 =(a+b)2 [ 完全平方和公式 ] 练习
a2 -2ab- b2 =(a-b)2 [ 完全平方差公式 ]
公式法中主要使用的公式有如下几个:
用平方差公式分解因式的关键:多项式是否能看成两个数的平方的差;
用完全平方公式分解因式的关键:在于判断一个多项式是否为一个完全平方式;
平方差公式:a2-b2=(a+b)(a-b)
完全平方公式:a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
公式法
练习题: 分解因式 x2-(2y)2
a2-b2=(a+b)(a-b) [ 平方差公式 ]
解: x2-(2y)2
=(x+2y)(x-2y)
练习题:
下列各式能用完全平方公式分解因式的是( )
A、x2+x+2y2 B、 x2 +4x-4
C、x2+4xy+y2 D、 y2 -4xy+4 x2
② a2 +2ab+ b2 =(a+b)2
a2 -2ab- b2 =(a-b)2
D
因式分解的一般步骤:
一提:先看多项式各项有无公因式,如有公因式则要先提取公因式;
二套:再看有几项,
如两项,则考虑用平方差公式;如三项,则考虑用完全平方公 式;
四查:最后用整式乘法检验一遍,并看各因式能否再分解,如能分解,应分解到不能再分解为止。
一般步骤
三变:若以上两步都不行,则将考虑将多项式变形,使之能“提”或能“套”。[如(x+y) -x-y=(x+y)(x+y-1)
第二步第二环节
1.分解因式:m2 – n2 + 2m - 2n (北京市)
解:
原式=(m2-n2) + (2m – 2n)
=( m + n )( m – n )+2( m – n )
=( m - n )( m + n +2)
2.分解因式: x3 – xy2 ( 沈阳市)
解:
原式= x ( x2 – y2 )
= x ( x + y )( x – y )
( x -y)3 - ( x -y)
解: ( x -y)3 - ( x -y)
= ( x -y) ( x -y + 1) ( x -y - 1)
分解因式: x3 – x = ___________
x( x 2 – 1) = x (x+1)(x-1)
解:
x(x+1)(x-1)
分解因式:(4x2+1)2 – 16x2
解:
(4x2+1)2 – 16x2
=(4x2+1+4x)(4x2+1-4x)
=(2x+1)2(2x-1)2
=(4x2+4x+1)(4x2-4x+1)
.将 x – xy2 分解因式______________
解:
x – xy2=x(1-y2)
=x(1+y)(1-y)
x(1+y)(1-y)
=[3(m+n)]2- (m-n)2
=[3(m+n)+ (m-n)][3(m+n)- (m-n)]
=(3m+3n+m-n)(3m+3n-m+n)
9(m+n)2-(m-n)2
=(4m+2n)(2m+4n)
=4(2m+n)(m+2n)
(广西)
简化计算
主要应用
多项式的除法
解方程
简化计算
(1)562+56×44 (2)1012 - 992
变式
若a=99,b=-1,则a2-2ab+b2=____________;
超级变变变
解方程:
x -9x=0
变式
解下列方程:
(3x- 4) - (3x+ 4) =48
多项式的除法
(2mp-3mq+4mr) ÷(2p-3q+4r)
变式:
20052+2005能被2006整除吗?
第三步
求证:对于自然数n,2n+4-2n能被30整除.
解:2n+4-2n=2n(24-1)=2n(16-1)=15×2n
=15×2×2n-1=30×2n-1.
∵n为自然数时,2n-1为整数,
∴2n+4-2n能被30整除.
典型例题解析
大
已知a、b、c是一个三角形的三边,判断代数式a2-b2 -c2 –2bc 的正负性。(提示: a2-b2 -c2 –2bc = a2-(b2+c2 +2bc )
比
一个矩形的面积为a3 -2ab+a ,宽为 a ,则矩形的长为_____________
( 安徽 )
解:
矩形的长=(a3-2ab+a)÷a
=a2 – 2b+1
a2 – 2b+1
(黄冈)
若a2-2a+1=0 , 2a2- 4a =_____
解法一:
由a2-2a+1=0得(a-1)2=0,∴a=1
∴ 2a2- 4a =2×12 - 4×1= -2
解法二:
由a2-2a+1=0得a2-2a=-1,
∴ 2a2- 4a =2(a2-2a)
=2×(-1)
=-2
解法三:
2a2- 4a= 2a2- 4a+2-2
=2(a2-2a+1)-2
=2×0-2=-2
-2
(广州)
如果 x2+x-1=0, 那么代数式 x3+2x2 -7的值为( )
x2+x-1=0得x2=1-x,
则x3+2x2-7=x(1-x)+2(1-x)-7
=x-x2+2-2x-7=-x2-x-5
=-(x2+x)-5=-(x2+x-1)-6
=-6
解:
A. 6 B. 8 C. -6 D. -8
C
(福州市)
(厦门市)
已知: a+b =m , ab = -4,
化简:(a-2)(b-2)的结果是( )
A. 6 ; B. 2m-8 ; C. 2m , D.-2m
D
(厦门市)
解:
(a-2)(b-2)
=ab-2a-2b+4
=ab-2(a+b)+4
=-4-2m+4
=-2m
已知 2n+2-n=k(n为正整数),
则4n+4-n=______(用含k的代数式示).
(烟台市)
K2 -2
解:
4n+4-n=(2n)2+(2-n)2
= (2n+2-n)2 -2n·2-n
= k2 - 2
在多项式4x2+1中添加一个单项式,使其成为一个完全平方式,则添加的单项式是________ (只写一个即可)
4x或 -4x
已知 a–b=b-c=3/5 , a2+b2+c2=1 ,ab+bc+ca=____
(宁波市)
解:
由已知得a+c=2b (1) ,a =3/5+b ,
∴(3/5+b)2+b2+(b-3/5 )2=1
c=b-3/5,
∵(a+b+c)2=a2+b2+c2+2ab+2bc+2ca
b2=7/75 ,
若 ( )
A. B. C. D.
(潍坊市)
解:
A
在日常生活中取款、上网等都需要密码,有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式 x4 – x4 , 因式分解的结果是(x –y)(x+y)(x2+y2), 若取x=9 ,y=9时,则各个因式的值是: (x-y)=0 , (x+y) =18 , (x2+y2) =162, 于是就可以把“018162”作为一个六位数的密码, 对于多项式 4x3 – xy2 , 取x =10 , y = 10 时, 用上述方法产生的密码是:___________________________
101030 ;
(写一个即可) (浙江)
或103010 ;
或301010
4x3 – xy2 = x (2x-y)(2x+y)
x=10 , 2x-y =10 , 2x+y =30
因式分解应进行到底.
如:分解因式:x4-4=(x2+2)(x2-2)
=(x2+2)(x+ )(x- ).
应在实数范围内将它分解到底.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
