人教版七年级数学上册第三章一元一次方程复习课件(共42张PPT)
文档属性
| 名称 | 人教版七年级数学上册第三章一元一次方程复习课件(共42张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 00:00:00 | ||
图片预览











文档简介
(共42张PPT)
任何人都可以成为自己想成为的那种人,任何人都可以实现自己的愿望,只要你愿意!
一元一次方程复习
课堂小练
1、解下列方程
2、一项工程甲单独做要40天完成,乙单独做需要50天完成,甲先单独做4天,然后两人合作,需要几天完成剩下的工程?
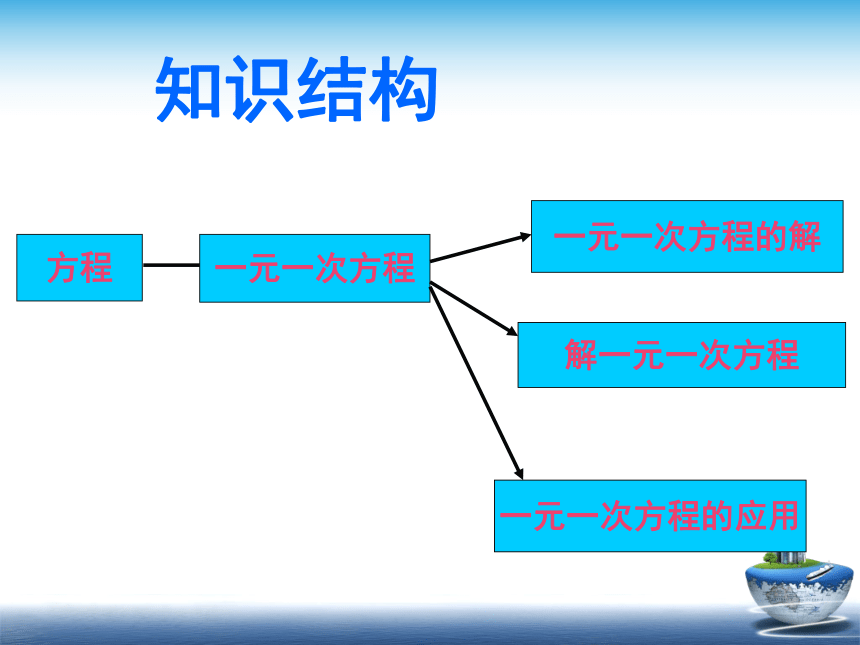
知识结构
方程
一元一次方程
解一元一次方程
一元一次方程的解
一元一次方程的应用
(一)概念
1.方程:含有未知数的等式。
2.一元一次方程:含有一个未知数,并且未知数的次数是1。
3. 方程的解:使方程的左右两边相等的未知数的值。表示形式:
4.解方程:求方程的解的过程。
1、什么是一元一次方程 (你们一定记得!)
(1)方程的两边都是整式
(2)只含有一个未知数
(3)未知数的指数是一次.
挑战记忆
判断下列各式中哪些是一元一次方程?
(1) 5x=0 (2)1+3x (3)y =4+y
(4)x+y=5 (5) (6) 3m+2=1–m
×
√
×
×
×
√
1、若x=2是方程ax+3=2x解,则a=_____
2、已知方程mx-4=2的解为x=-3,则m=____
-2
2.方程的解:
使方程左右两边相等的未知数的值
练习:
方法点拨:把解代入方程
(1)去分母:
不要漏乘不含分母的项
(2)去括号:
去括号后的符号变化,并且不要漏乘括号中的每一项
例:去括号
A、+(2X- 5)= ___________ B、- (2X- 5)=__________
C、3(3X+1)=___________ D、-2(3X- 5)= _________
(3)移项:
移动的项要变号
例:方程3X+20=4X-25+5
移项正确的是:A、3X-4X=-5-25-20
B、 3X-4X=-25+5-20
3、解一元一次方程的一般步骤
3(3Y-1)-12=2(5Y-7)
2X- 5
- 2X+5
9X+3
- 6X+10
√
×
1.若 是一元一次方程,则 的值是
解:由一元一次方程定义,得
2.已知3是关于 的方程 的解,则 的值是( )
-5 B. 5 C. 7 D. 2
B
3. 下列方程中一元一次方程的个数是( )
①
②
③
④
⑤
⑥
3个 B.4个 C. 5个 D. 6个
A
4. 若关于 的方程 的解是
则 的值是
1
5. 已知 是方程 的解,求关于 的方程 的解。
解:将 代入方程 中,得
解得
将 代入方程 中,得
解得
6. 已知方程 是关于 的一元一次方程,则 的值是( )。
B. 1 C. -1 D. 0或1
B
7. 若 是关于 的方程 的解,则 的值是( )
B. 1 C. 6 D. 3
C
8. 若 与 的值互为相反数,求
解:
解题关键:由相反数的意义构造含有m的一元一次方程,解出m.
解得,
9. 已知 的值与 互为倒数,求 的值。
分析:根据倒数的意义,构造出含x的一元一次方程,求出x 的值。
解:由倒数的意义,得
解得
10. 如果一个数与4的差的绝对值等于2,那么这
个数等于多少?
分析:由于绝对值等于2的数有两个,若设这个数为 ,则可构造两个一元一次方程: 或 ,分别求解。
解:设这个数为 ,由题意得
即 或
解得 或
因此这个数是6或2
11. 若 与 是同类项,则
解:根据同类项的定义,由已知得
25
(二)等式的性质
性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
如果 ,那么
性质2:等式两乘同一个数,或除以同一个不为0的数,结果仍相等。
如果 ,那么
如果 ,那么
(1)如果x=y,那么 ( )
(2)如果x=y,那么 ( )
(3)如果x=y,那么 ( )
(4)如果x=y,那么 ( )
(5)如果x=y,那么 ( )
1.判断对错,对的说明根据等式的哪一条性质;错的说出为什么。
×
√
×
×
√
相信你能行
2. 如果 ,那么下列等式不一定成立的是( )
D
步骤 具体做法 依据 注意事项
去分母
去括号
移项
合并同类项
系数化为1
在方程两边都乘以各分母的最小公倍数
等式
性质2
1.不要漏乘不含分母的项
一般先去小括号,再去中括号,最后去大括号
分配律 去括号法则
1.不要漏乘括号中的每一项
把含有未知数的项移到方程一边,其它项都移到方程另一边,注意移项要变号
移项
法则
1.移动的项一定要变号,
不移的项不变号
2.注意移项较多时不要漏项
把方程变为ax=b
(a≠0 ) 的最简形式
合并同类项法则
2.字母和字母的指数不变
将方程两边都除以未知数系数a,得解x=b/a
等式性质2
解的分子,分母位置不要颠倒
1.把系数相加
相信你能行
2.分子作为一个整体要加上括号
2.括号前是负号,各项要变号
解方程
解:去分母,得
去括号,得
移项,得
∴
去分母得
去括号,得
移项,合并同类项,得
下面方程的解法对吗?若不对,请改正 。
不对
两边同时除以10,得
火眼金睛
例:解下列方程:
解:原方程可化为:
注意:如果分母不是整数的方程可以应用分数的基本性质转化成整数,这样有利于去分母。
去分母, 得5x –(1.5 - x)= 1
去括号,得 5x – 1.5 + x = 1
移项, 得 5x + x = 1 + 1.5
合并同类项,得 6x= 2.5
两边同除以6, 得x=
此题还有其它的
解法吗?
解:化分母为整数得:
去分母得:
去括号得:
移项得:
合并得:
系数化为1得:
1、若x=2是方程ax+3=2x解,则a=_____
2、已知方程mx- 4=2的解为x=-3,则m =____
中考链接
-2
3、小李在解方程5a—x=13(x为未知数)时,误将-x看作+x,得方程的解为x=-2,则原方程的解为( )
A.x=-3 B.x=0 C.x=2 D.x=1
4、中央电视台2套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则三个球体的重量等于( )个正方体的重量.
A.2 B.3 C.4 D.5
C
D
(1)3(x-2)=2-5(x-2) (2) 2(x+3)-5(1-x)=3(x-1)
(3) 3(x+1)-2(x+2)=2x+3 (4) 3(x-2)+1=x-(2x-1)
当堂检测
解下列方程
应用题中见数量关系
类型 基本数量关系 等量关系
相遇问题 路程=速度×时间 甲走的路程+乙走的路程=两地距离
追及问题 同地不同时出发:前者走的路程=追者走的路程
同时不同地出发:前者走的路程+两地距离=追者所走的路程
应用题中见数量关系
类型 基本数量关系 等量关系
工程问题 工作总量=工作效率×工作时间 各部分工作量之和=1
水速问题
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
应用题中见数量关系
类型 基本数量关系 等量关系
利润率问题 利润=售价-进价
利润率= ×100%
售价=进价×(1+利润率)
抓住价格升降对利润率的影响来考虑
储蓄问题 利息=本金×利率×期数
本息和=本金+利息
利润
进价
解下列方程
1.
2.
(四)实际问题与一元一次方程
用一元一次方程解决实际问题的基本步骤:
1. 审:审题,分析题目中的数量关系;
2. 设:设适当的未知数,并表示未知量;
3. 列:根据题目中的数量关系列方程;
4. 解:解这个方程;
5. 答:检验并答.
1.西安站和武汉站相距1500km,一列慢车从西安开出,速度为68km/h,一列快车从武汉开出,速度为85km/h,若两车相向而行,慢车先开0.5小时,快车行使几小时后两车相遇?
西安(慢车)
(快车)武汉
慢车先行路程
快车路程
(慢车先行路程+慢车后行路程)+快车路程=总路程
慢车后行路程
西安
武汉
相遇
相遇问题:不同时出发 (三条线段 )
2. 某工厂计划为震区生产A、B两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套A型桌椅(一桌二椅), 一套B型桌椅(一桌三椅)需木料 .
(1)问需要生产A型桌椅多少套?
(2)已知每套A型桌椅生产成本为100元,运费2元;每套B型桌椅的生产成本为120元,运费4元,现要把桌椅全部生产完并运往震区,求所需总费用。(总费用=生产成本+运费)
分析:题中等量关系有:A套数+B套数=500,椅子总数=学生总数。
解:(1)设生产A型桌椅 套,则B型为 套,由题得
解得, 则
(2)总费用为
答:(1)需生产A型桌椅250套;(2)所需总费用为56500元。
3. 某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元。甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售。那么,什么情况下到甲商场购买更优惠?
甲费用=餐桌数×单价+(椅数-桌数) ×单价
乙费用=[餐桌数×单价+椅数×单价] ×85%
4. 某校校长带领本校三好学生去北京旅游,甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠。”乙旅行社说:“包括校长在内全部按全票的六折优惠。”全票价是1000元。
(1)设学生数为 ,甲旅行社收费为 ,乙旅行社收费为 ,分别计算两家旅行社的收费。
(2)当学生人数是多少时,两家旅行社收费一样?
(3)若有5位学生,哪家旅行社便宜?
5.有一群鸽子和一些鸽笼,如果每个鸽笼住6只鸽子,则剩余3只鸽子无鸽笼可住;如果再飞来5只鸽子,连同原来的鸽子,每个鸽笼刚好住8只鸽子。原来有多少只鸽子和多少个鸽笼?
提示:鸽子数与鸽笼数是一定的。
(1)鸽子数=鸽笼数×6+3
(2)鸽子数=鸽笼数×8-5
6. 一个两位数,个位上的数是十位上的数的2倍,如果把十位与个位上的数对调,那么所得的两位数比原两位数大36,求:原来的两位数是多少?
分析:设十位上的数字X,则个位上的数是2x
十 位 个 位 表 示
原 数
新 数
x
2x
2x
x
10×2x+x
10x+2x
★进价(成本价):
指商家批发进货时,所需要的付出的金额;
★售价:指商品成交时的实际价格;
★利润:指商品售价与进价之间的差,老板赚的钱;
一件商品的标价为50元,现以八折销售,售价为 元,如果进价为25元,则它的利润为 元,利润率为_______。
★标价(原价):出售商品时,标签上所标明的价格;
★利润率:指利润与进价的比,用百分数表示。
注意:利润率总是,相对于进价而言。
40
15
60%
= 商品售价—商品进价
商品利润
利润率=
进价
利润
×100%
商品售价=
标价×
折扣数
10
商品进价
商品售价=
×(1+利润率)
熟 记 : 公 式
7.商店对某种商品作调价,按原价的8折出售,此时商品的利润率是10%,此商品的进价为1600元。问商品的原价是多少?
条件
按原价的8折出售
按8折出售时的利润率是10%
商品的进价为1600元
——原价的80%为售价
——利润率
——进价
问题
商品原价是多少?
任何人都可以成为自己想成为的那种人,任何人都可以实现自己的愿望,只要你愿意!
一元一次方程复习
课堂小练
1、解下列方程
2、一项工程甲单独做要40天完成,乙单独做需要50天完成,甲先单独做4天,然后两人合作,需要几天完成剩下的工程?
知识结构
方程
一元一次方程
解一元一次方程
一元一次方程的解
一元一次方程的应用
(一)概念
1.方程:含有未知数的等式。
2.一元一次方程:含有一个未知数,并且未知数的次数是1。
3. 方程的解:使方程的左右两边相等的未知数的值。表示形式:
4.解方程:求方程的解的过程。
1、什么是一元一次方程 (你们一定记得!)
(1)方程的两边都是整式
(2)只含有一个未知数
(3)未知数的指数是一次.
挑战记忆
判断下列各式中哪些是一元一次方程?
(1) 5x=0 (2)1+3x (3)y =4+y
(4)x+y=5 (5) (6) 3m+2=1–m
×
√
×
×
×
√
1、若x=2是方程ax+3=2x解,则a=_____
2、已知方程mx-4=2的解为x=-3,则m=____
-2
2.方程的解:
使方程左右两边相等的未知数的值
练习:
方法点拨:把解代入方程
(1)去分母:
不要漏乘不含分母的项
(2)去括号:
去括号后的符号变化,并且不要漏乘括号中的每一项
例:去括号
A、+(2X- 5)= ___________ B、- (2X- 5)=__________
C、3(3X+1)=___________ D、-2(3X- 5)= _________
(3)移项:
移动的项要变号
例:方程3X+20=4X-25+5
移项正确的是:A、3X-4X=-5-25-20
B、 3X-4X=-25+5-20
3、解一元一次方程的一般步骤
3(3Y-1)-12=2(5Y-7)
2X- 5
- 2X+5
9X+3
- 6X+10
√
×
1.若 是一元一次方程,则 的值是
解:由一元一次方程定义,得
2.已知3是关于 的方程 的解,则 的值是( )
-5 B. 5 C. 7 D. 2
B
3. 下列方程中一元一次方程的个数是( )
①
②
③
④
⑤
⑥
3个 B.4个 C. 5个 D. 6个
A
4. 若关于 的方程 的解是
则 的值是
1
5. 已知 是方程 的解,求关于 的方程 的解。
解:将 代入方程 中,得
解得
将 代入方程 中,得
解得
6. 已知方程 是关于 的一元一次方程,则 的值是( )。
B. 1 C. -1 D. 0或1
B
7. 若 是关于 的方程 的解,则 的值是( )
B. 1 C. 6 D. 3
C
8. 若 与 的值互为相反数,求
解:
解题关键:由相反数的意义构造含有m的一元一次方程,解出m.
解得,
9. 已知 的值与 互为倒数,求 的值。
分析:根据倒数的意义,构造出含x的一元一次方程,求出x 的值。
解:由倒数的意义,得
解得
10. 如果一个数与4的差的绝对值等于2,那么这
个数等于多少?
分析:由于绝对值等于2的数有两个,若设这个数为 ,则可构造两个一元一次方程: 或 ,分别求解。
解:设这个数为 ,由题意得
即 或
解得 或
因此这个数是6或2
11. 若 与 是同类项,则
解:根据同类项的定义,由已知得
25
(二)等式的性质
性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
如果 ,那么
性质2:等式两乘同一个数,或除以同一个不为0的数,结果仍相等。
如果 ,那么
如果 ,那么
(1)如果x=y,那么 ( )
(2)如果x=y,那么 ( )
(3)如果x=y,那么 ( )
(4)如果x=y,那么 ( )
(5)如果x=y,那么 ( )
1.判断对错,对的说明根据等式的哪一条性质;错的说出为什么。
×
√
×
×
√
相信你能行
2. 如果 ,那么下列等式不一定成立的是( )
D
步骤 具体做法 依据 注意事项
去分母
去括号
移项
合并同类项
系数化为1
在方程两边都乘以各分母的最小公倍数
等式
性质2
1.不要漏乘不含分母的项
一般先去小括号,再去中括号,最后去大括号
分配律 去括号法则
1.不要漏乘括号中的每一项
把含有未知数的项移到方程一边,其它项都移到方程另一边,注意移项要变号
移项
法则
1.移动的项一定要变号,
不移的项不变号
2.注意移项较多时不要漏项
把方程变为ax=b
(a≠0 ) 的最简形式
合并同类项法则
2.字母和字母的指数不变
将方程两边都除以未知数系数a,得解x=b/a
等式性质2
解的分子,分母位置不要颠倒
1.把系数相加
相信你能行
2.分子作为一个整体要加上括号
2.括号前是负号,各项要变号
解方程
解:去分母,得
去括号,得
移项,得
∴
去分母得
去括号,得
移项,合并同类项,得
下面方程的解法对吗?若不对,请改正 。
不对
两边同时除以10,得
火眼金睛
例:解下列方程:
解:原方程可化为:
注意:如果分母不是整数的方程可以应用分数的基本性质转化成整数,这样有利于去分母。
去分母, 得5x –(1.5 - x)= 1
去括号,得 5x – 1.5 + x = 1
移项, 得 5x + x = 1 + 1.5
合并同类项,得 6x= 2.5
两边同除以6, 得x=
此题还有其它的
解法吗?
解:化分母为整数得:
去分母得:
去括号得:
移项得:
合并得:
系数化为1得:
1、若x=2是方程ax+3=2x解,则a=_____
2、已知方程mx- 4=2的解为x=-3,则m =____
中考链接
-2
3、小李在解方程5a—x=13(x为未知数)时,误将-x看作+x,得方程的解为x=-2,则原方程的解为( )
A.x=-3 B.x=0 C.x=2 D.x=1
4、中央电视台2套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则三个球体的重量等于( )个正方体的重量.
A.2 B.3 C.4 D.5
C
D
(1)3(x-2)=2-5(x-2) (2) 2(x+3)-5(1-x)=3(x-1)
(3) 3(x+1)-2(x+2)=2x+3 (4) 3(x-2)+1=x-(2x-1)
当堂检测
解下列方程
应用题中见数量关系
类型 基本数量关系 等量关系
相遇问题 路程=速度×时间 甲走的路程+乙走的路程=两地距离
追及问题 同地不同时出发:前者走的路程=追者走的路程
同时不同地出发:前者走的路程+两地距离=追者所走的路程
应用题中见数量关系
类型 基本数量关系 等量关系
工程问题 工作总量=工作效率×工作时间 各部分工作量之和=1
水速问题
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
应用题中见数量关系
类型 基本数量关系 等量关系
利润率问题 利润=售价-进价
利润率= ×100%
售价=进价×(1+利润率)
抓住价格升降对利润率的影响来考虑
储蓄问题 利息=本金×利率×期数
本息和=本金+利息
利润
进价
解下列方程
1.
2.
(四)实际问题与一元一次方程
用一元一次方程解决实际问题的基本步骤:
1. 审:审题,分析题目中的数量关系;
2. 设:设适当的未知数,并表示未知量;
3. 列:根据题目中的数量关系列方程;
4. 解:解这个方程;
5. 答:检验并答.
1.西安站和武汉站相距1500km,一列慢车从西安开出,速度为68km/h,一列快车从武汉开出,速度为85km/h,若两车相向而行,慢车先开0.5小时,快车行使几小时后两车相遇?
西安(慢车)
(快车)武汉
慢车先行路程
快车路程
(慢车先行路程+慢车后行路程)+快车路程=总路程
慢车后行路程
西安
武汉
相遇
相遇问题:不同时出发 (三条线段 )
2. 某工厂计划为震区生产A、B两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套A型桌椅(一桌二椅), 一套B型桌椅(一桌三椅)需木料 .
(1)问需要生产A型桌椅多少套?
(2)已知每套A型桌椅生产成本为100元,运费2元;每套B型桌椅的生产成本为120元,运费4元,现要把桌椅全部生产完并运往震区,求所需总费用。(总费用=生产成本+运费)
分析:题中等量关系有:A套数+B套数=500,椅子总数=学生总数。
解:(1)设生产A型桌椅 套,则B型为 套,由题得
解得, 则
(2)总费用为
答:(1)需生产A型桌椅250套;(2)所需总费用为56500元。
3. 某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元。甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售。那么,什么情况下到甲商场购买更优惠?
甲费用=餐桌数×单价+(椅数-桌数) ×单价
乙费用=[餐桌数×单价+椅数×单价] ×85%
4. 某校校长带领本校三好学生去北京旅游,甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠。”乙旅行社说:“包括校长在内全部按全票的六折优惠。”全票价是1000元。
(1)设学生数为 ,甲旅行社收费为 ,乙旅行社收费为 ,分别计算两家旅行社的收费。
(2)当学生人数是多少时,两家旅行社收费一样?
(3)若有5位学生,哪家旅行社便宜?
5.有一群鸽子和一些鸽笼,如果每个鸽笼住6只鸽子,则剩余3只鸽子无鸽笼可住;如果再飞来5只鸽子,连同原来的鸽子,每个鸽笼刚好住8只鸽子。原来有多少只鸽子和多少个鸽笼?
提示:鸽子数与鸽笼数是一定的。
(1)鸽子数=鸽笼数×6+3
(2)鸽子数=鸽笼数×8-5
6. 一个两位数,个位上的数是十位上的数的2倍,如果把十位与个位上的数对调,那么所得的两位数比原两位数大36,求:原来的两位数是多少?
分析:设十位上的数字X,则个位上的数是2x
十 位 个 位 表 示
原 数
新 数
x
2x
2x
x
10×2x+x
10x+2x
★进价(成本价):
指商家批发进货时,所需要的付出的金额;
★售价:指商品成交时的实际价格;
★利润:指商品售价与进价之间的差,老板赚的钱;
一件商品的标价为50元,现以八折销售,售价为 元,如果进价为25元,则它的利润为 元,利润率为_______。
★标价(原价):出售商品时,标签上所标明的价格;
★利润率:指利润与进价的比,用百分数表示。
注意:利润率总是,相对于进价而言。
40
15
60%
= 商品售价—商品进价
商品利润
利润率=
进价
利润
×100%
商品售价=
标价×
折扣数
10
商品进价
商品售价=
×(1+利润率)
熟 记 : 公 式
7.商店对某种商品作调价,按原价的8折出售,此时商品的利润率是10%,此商品的进价为1600元。问商品的原价是多少?
条件
按原价的8折出售
按8折出售时的利润率是10%
商品的进价为1600元
——原价的80%为售价
——利润率
——进价
问题
商品原价是多少?
