9.1.1 认识三角形(1)
图片预览



文档简介
§9.1 三角形
第一课时
【学习内容】
§9.1.1 认识三角形(1)
【学习目标】
1、了解三角形、三角形的边、顶点、内角、外角等概念;会准确地表示三角形及其边、角.
2、能按角、边分别将三角形分类;
3、理解等腰三角形、等边三角形的概念.
【学习重点和难点】
1、学习重点:三角形内角、外角、等腰三角形、等边三角形等概念;
2、学习难点:三角形的外角.
【学习过程】
一、知识回顾
1、回顾线段、射线、直线相关知识,填写下表:
名称 特征 延伸性 端点个数 表示方法 性质
线段
直线
射线
2、由 组成的图形叫做角,角也可以看成是
的图形.射线的端点叫做角的顶点,起始位置的射线叫做角的始边,终止位置的射线叫做角的终边.
3、如图9.1-1,图中一共有 个小于平角的角,它们分
别是
.
二、预习导学
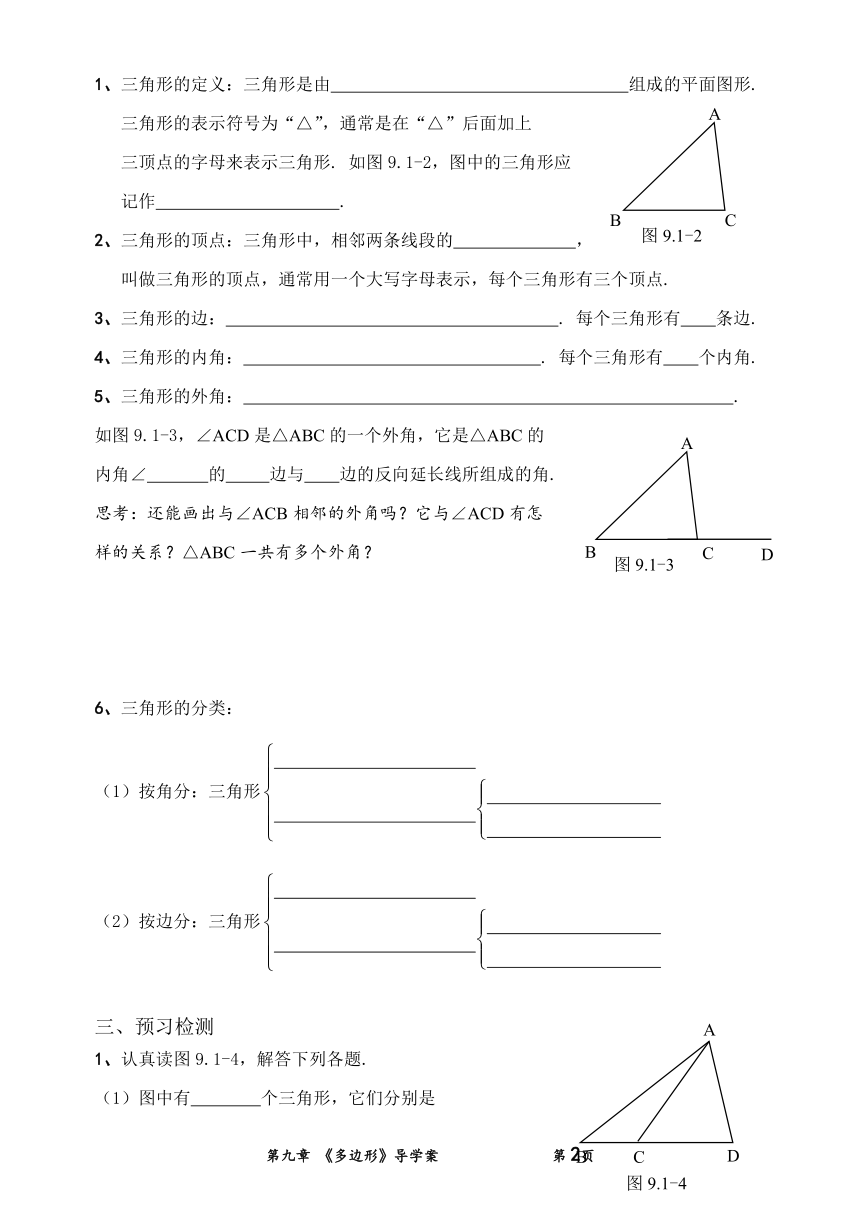
1、三角形的定义:三角形是由 组成的平面图形.
三角形的表示符号为“△”,通常是在“△”后面加上
三顶点的字母来表示三角形. 如图9.1-2,图中的三角形应
记作 .
2、三角形的顶点:三角形中,相邻两条线段的 ,
叫做三角形的顶点,通常用一个大写字母表示,每个三角形有三个顶点.
3、三角形的边: . 每个三角形有 条边.
4、三角形的内角: . 每个三角形有 个内角.
5、三角形的外角: .
如图9.1-3,∠ACD是△ABC的一个外角,它是△ABC的
内角∠ 的 边与 边的反向延长线所组成的角.
思考:还能画出与∠ACB相邻的外角吗?它与∠ACD有怎
样的关系?△ABC一共有多个外角?
6、三角形的分类:
(1)按角分:三角形
(2)按边分:三角形
三、预习检测
1、认真读图9.1-4,解答下列各题.
(1)图中有 个三角形,它们分别是
;
(2)△ACD的三边分别是 ,
三个内角分别是 ,它的外角是 .
(3)∠ACB是△ 的内角,它的对边是 ,∠ACD是△ 的外角.
BD是△ 的边,它的对角是 .
2、如图9.1-5,图中以BC为边的三角形共有 个;
它们分别 .
在△ABD中,∠A是 边的对角, ∠ADB是
△ 的内角,又是 的一个外角.
四、典例剖析
例1 如图9.1-6,图中的三角形可以表示为 ,
它的三边分别是 ,它的三个内角分别
是 、 、 ;与∠1的相邻的外
角是 ,∠1+∠BCD = .
例2 下列关于等腰三角形的说法正确的有 .
(1)有且只有两条边相等的三角形是等腰三角形;(2)有两条边相等的三角形是等腰三角形;(3)等腰三角形都是锐角三角形;(4)三角形可分为不等边三角形、等腰三角形、等边三角形.
例3 在△ABC中,∠A=∠B=∠C,试判断△ABC的形状.
五、分层练习
1、如图9.1-7,∠B是 的内角,
△ABD的外角是 ; 在△ABE中,AE所对的角是
;在△ADE中AD是 的对边,在△ADC
中AD是 的对边.
2、若有一条公共边的两个三角形称为一对“共边三角形”,在图9.1-8中,以BC为公共边的“共边三角形” 有 .
3、如图9.1-9,在△ABC中,∠ACB是钝角,让点C在射线
BD上向右移动,则下列说法正确的是( ).
A、△ABC将变为锐角三角形,不再变为钝角三角形;
B、△ABC将先变为直角三角形,然后变为锐角三角形,而
再不会是钝角三角形;
C、△ABC将先变为直角三角形,然后变为锐角三角形,接
着又由锐角三角形变为钝角三角形;
D、△ABC先由钝角三角形变为直角三角形,再变为锐角三
角形,接着又变为直角三角形,然后再次变为钝角三角形.
4、若三角形的一个外角为115°,则与这个外角相邻的内角等于 °;若一个三角形的一个外角等于它相邻内角的2倍,则这个外角的度数是 °.
5、已知,三角形的三边的比是3︰4︰5,且最大边长与最小边长的差是4,求这个三角形的三条边的长.
6、如图9.1-10,在△ABC中,∠ACB=90°,CD⊥AB于D,AB=10,AC=8,BC=6.
(1)求△ABC的面积;(2)求高CD的长.
六、学习心得
七、课堂作业
八、家庭作业
九、课外延伸和拓展
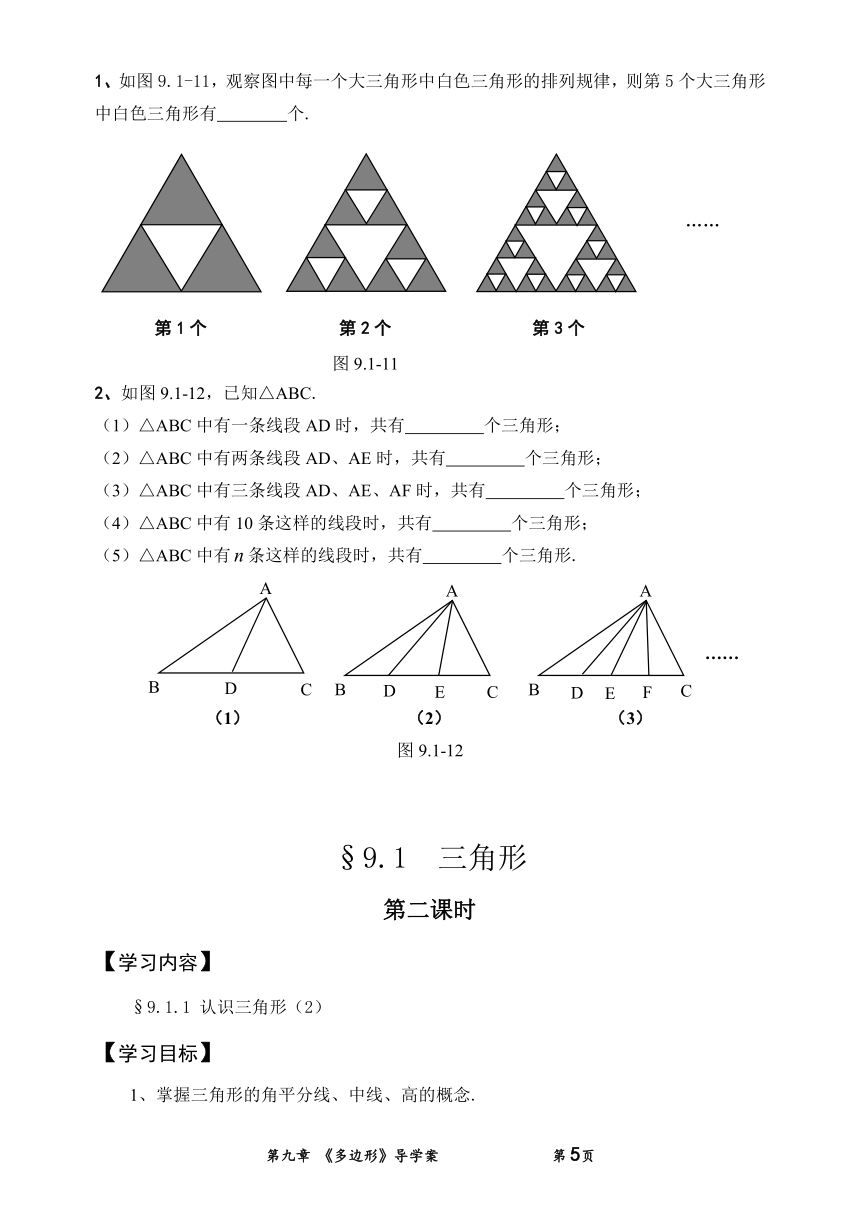
1、如图9.1-11,观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有 个.
第1个 第2个 第3个
2、如图9.1-12,已知△ABC.
(1)△ABC中有一条线段AD时,共有 个三角形;
(2)△ABC中有两条线段AD、AE时,共有 个三角形;
(3)△ABC中有三条线段AD、AE、AF时,共有 个三角形;
(4)△ABC中有10条这样的线段时,共有 个三角形;
(5)△ABC中有条这样的线段时,共有 个三角形.
……
(1) (2) (3)
图9.1-12
§9.1 三角形
第二课时
【学习内容】
§9.1.1 认识三角形(2)
【学习目标】
1、掌握三角形的角平分线、中线、高的概念.
2、会画出任意三角形的角平分线、中线、高;
3、能运用三角形的角平分线、中线、高的定义解决一些简单的问题.
【学习重点和难点】
1、学习重点:三角形角平分线、中线、高的概念及其画法;
2、学习难点:钝角三角形高的画法.
【学习过程】
一、知识回顾
1、如图9.1-13,图中共有 个三角形,其中以BC为
一边的三角形有 ;
以∠1为内角的三角形是 ;
以∠2为外角的三角形是 .
2、在下列条件中,能判定△ABC是直角三形的是 .
(1)∠A+∠B=90°; (2)∠A︰∠B︰∠C=1︰2︰3; (3)∠A= 90°-∠B;
(4)∠A=∠B=∠C; (5)∠A=2∠B=3∠C. (6)AC⊥BC于点C.
3、(1)已知∠AOB,作∠AOB的平分线OC; (2)已知直线AB外一点P,过点P作PC⊥AB于点C.
二、预习导学
1、三角形的中线:三角形的 与 的连线叫三角形的中线.
(1)三角形中线的判定:
∵ 点D是BC边的中点(BD=CD)
∴
(2)三角形中线的性质:
∵AD是△ABC的中线
∴
2、三角形的角平分线:三角形 与 之间的线段叫三角形的角平分线.
(1)三角形角平分线的判定:
∵∠1=∠2
∴
(2)三角形角平分线的性质:
∵ CE是△ABC的角平分线
∴
3、三角形的高:过三角形顶点作对边的垂线, 与 之间的线段叫三角形的高.
(1)三角形高的判定:
∵BF⊥AC于点F
∴
(2)三角形高的性质:
∵BF是△ABC的高
∴
4、做一做:
(1)分别画出锐角△ABC的中线、角平分线和高.
作出中线 作出角平分线 作出高
(2)分别画出直角△ABC的中线、角平分线和高.
作出中线 作出角平分线 作出高
(3)分别画出钝角△ABC的中线、角平分线和高.
作出中线 作出角平分线 作出高
我的发现:
(1)三角形有 条中线; 条角平分线; 条高.
(2)三角形的中线、角平分线、高都是 ,一个端点是三角形的 ,另一个端点在 .
(3)任意三角形的三条中线都在三角形的 ,并交于 .
(4)任意三角形的三条角平分线都在三角形的 ,并交于 .
(5)锐角三角形的三条高都在三角形的 ,并交于 .
直角三角形的斜边上的高在三角形的 ,另两条高恰好是 ,三条高交于 .
钝角三角形的最大边上的高在三角形的 ,另两条高在三角形的 ,三条高交于 .
三、预习检测
1、如图9.1-14,在△ABC中,∠1=∠2,G为AD中点,延长
BG交AC于E,F为AB上一点,CF⊥AD于H,下列说法
正确的是 .
① AD是△ABE的角平分线;② BE是△ABD边AD上的中线;
③ BE是△ABC边AC上的中线;④ CH是△ACD边AD上的高.
2、如图△ABC,画边BC上的高,下面的画法正确吗?若不正确,请画出正确的高.
(1) (2) (3) (4)
3、如图9.1-15,AD⊥BC于D,以AD为高的
三角形有 .
四、典例剖析
例1 如图9.1-16,AD是△ABC的中线,AB=5,AC=3.
(1)求△ABD与△ADC的周长相差多少?
(2)猜想△ABD与△ADC的面积有怎样的关系,
并证明你的猜想.
例2 如图9.1-17,在△ABC中,∠A=80°,BD、CD分别平分∠ABC、∠ACB.
求∠BDC的度数.
例3 如图9.1-18,在△ABC中AE是∠BAC的平分线,
AF是BC边上的高,∠B=35°,∠C=65°.
求∠EAF的度数.
五、分层练习
1、下列说法中正确的是( ).
A、三角形的中线就是过顶点平分对边的直线;
B、三角形的高就是顶点到对边的距离;
C、三角形的角分线就是三角形的内角的平分线
D、三角形的三条中线必交于一点.
2、三角形一边上的中线把原三角形分成两个( ).
A、形状相同的三角形; B、面积相等的三角形;
C、直角三角形; D、周长相等的三角形.
3、如图9-1-19,BD=DE=EF=CF,图中共有 个三角形,
AF是△ 的中线,AE是△ 的中线.
4、如图9.1-20,已知AC⊥BC,CD⊥AB,DE⊥BC,则在△ABC中, 是BC边上的高;△BCD中, 是BC边上的高;△ABE中, 是BE边上的高;△ACD中, 是CD边上的高.
5、如图9.1-21,△ABC的三条角平分线交于一点G,∠BAC=76°,∠ABE=20°.
求∠BEC、∠ADC、∠DGC的度数.
六、学习心得
七、课堂作业
八、家庭作业
九、课外延伸和拓展
1、如图,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm,
AB=5cm,CD是AB边上的高,求CD的长度.
2、在等腰△ABC中,AB=AC,一腰上的中线将这个等腰三角形的周长分这21和12两部分,求△ABC的腰长和底边长.
3、如图,点O是等边三角形内任意一点,OD⊥AB,
OE⊥BC,OF⊥AC,高AM⊥BC.
试说明OD+OE+OF=AM.
§9.1 三角形
第三课时
【学习内容】
§9.1.2 三角形的外角和(1)
【学习目标】
1、探索并掌握三角形外角的性质、三角形的外角和定理;
2、能运用平行线等知识证明三角形外角的性质1、三角形的外角和是360°;
3、能运用三角形外角的性质、三角形的外角和定理进行简单的计算和说理.
【学习重点和难点】
1、学习重点:三角形外角的性质、三角形外角和定理;
2、学习难点:运用三角形外角的性质、三角形外角和定理进行简单的计算和说理.
【学习过程】
一、知识回顾
1、什么叫三角形?三角形的内角?三形的外角?
2、三角形的内角和定理: .
3、如图9.1-22,点D是△ABC的BC边上一点,已知∠BAD=35°,
∠B=45°,则∠ADB= °,∠ADC= °.
二、预习导学
1、一个三角形的每一个外角对应一个 的内角
和两个 的内角.
如图9.1-23,∠CBD是△ABC的一个外角,与∠CBD相邻的
内角是 ,与∠CBD不相邻的内角是 .
∠CBD+∠ABC= °.
2、三角形外角的性质
(1)三角形的一个外角等于 的两个内角的和.
(2)三角形的一个外角大于任何一个 的内角.
如图9.1-24,∠CBD是△ABC的一个外角.
求证:∠CBD=∠A+∠C.
3、与三角形的每个内角相邻的外角分别有两个,这两个外角是 ;从与每个内角相邻的两个外角中分别取一个相加,得到的和叫做 .
4、三角形的外角和定理: .
如图9.1-25,∠1、∠2、∠3分别是△ABC的外角.
求证:∠1+∠2+∠3=360°.
想一想:
你还有别的方法可以证明∠1+∠2+∠3=360°吗?试结合图9.1-26写出你的证明过程.
三、预习检测
1、求下列各图中∠1的度数.
解:(1)∠1= °; (2)∠1= °; (3)∠1= °.
2、如图9.1-27,在△ABC中,∠A=35°,∠CBD=115°.
求∠BCE的度数.
四、典例剖析
例1 如图9.1-28,点D是△ABC的BC边上一点,
∠C=∠CAD,∠ADB=70°,∠BAC=80°.
求∠B的度数.
例2 如图9.1-29,∠A=56°,∠ABD=20°,∠ACO=32°.
求∠BOC的度数.
例3 如图9.1-30,△ABC的外角∠ACE的平分线交BA延长线于点D.
证明:∠BAC>∠B.
五、分层练习
1、下列说法错误的是( ).
A、一个三角表中至少有一个角不大于60°;
B、三角形的一个外角等于与它不相邻的两个内角的和;
C、三角形的一个外角大于它的一个内角.
D、若一个三角形的一个角的外角与它相邻的内角相等,那
么这个三角形是直角三角形;
2、如图9.1-31,在△ABC中,点D是BC延长线上一点,
点F是AB边上一点,延长CA到E,连结EF.
则∠1、∠2、∠3的大小关系是 .
3、如图9.1-32,在△ABC中,∠A=60°,BD、CE分别是AC、AB边上的高,H是BD、CE的交点,求∠BHC的度数.
六、学习心得
七、课堂作业
八、家庭作业
九、课外延伸和拓展
1、如图9.1-33,已知∠1=∠2,∠BAC=70°,求∠DEF度数.
2、如图9.1-34,求证:∠D>∠A.
§9.1 三角形
第四课时
【学习内容】
§9.1.2 三角形的外角和(2)
【学习目标】
1、复习巩固三角形的外角的性质、三角形的外角和定理;
3、能熟练地运用三角形外角的性质、三角形的外角和进行计算和说理.
【学习重点和难点】
1、学习重点:三角形外角的性质、三角形外角和定理的应用;
2、学习难点:灵活运用三角形的外角性质和外角和定理.
【学习过程】
一、知识回顾
1、三角形的外角和定理:在三角形的每一个顶点取一个外角,所得的和是三角形的外角和,三角形的外角和等于 .
2、三角形外角的性质
(1)三角形的一个外角等于 .
(2)三角形的一个内角大于 .
3、如图9.1-36,在△ABC中,AD平分∠BAC,∠B=50°,∠C=68°.
求∠ADC的度数.
二、典例剖析
例1 如图9.1-37,AE是△ABC的外角∠CAD的角平分线,∠B=35°,∠EAD=60°.
求∠ACE的度数.
例2 如图9.1-38,在△ABC中,∠C=50°,若沿图中虚线MN剪去∠C.
求∠1+∠2的度数.
例3 如图9.1-39,五角星ABCDE中,求∠A+∠B+∠C+∠D+∠E的度数.
三、分层练习
1、 如图9.1-40,∠CAD=120°,∠C=40°,则∠B= °.
2、 在△ABC中,∠A、∠B、∠C相邻外角的比是2︰3︰4,
则∠A= °,∠B= °,∠C= °.
3、 在△ABC中,与∠C相邻的外角是120°,∠A的度数是∠B的度
数的.求△ABC各内角的度数.
4、 如图9.1-41,∠A=50°,∠B=35°∠C=25°.
求∠BDC的度数.
5、 如图9.1-42,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
四、学习心得
五、课堂作业
六、家庭作业
七、课外延伸和拓展
1、 一个零件的形状如图9.1-43所示,按规定∠A=90°,∠B=30°,∠D=20°. 李师傅量得∠BCD=142°,就断定这个零件不合格.
李师傅的说法正确吗?请说明理由.
2、如图9.1-44,在△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=80°,∠C=40°,求∠DAE的度数.
(2)若∠B -∠C= 40°,你能求出∠DAE的度数吗?
如果能,请求出∠DAE的度数.
(3)通过(1)、(2)的计算,请写出∠DAE与∠B、
∠C之间的关系.
§9.1 三角形
第五课时
【学习内容】
§9.1.3 三角形的三边关系
【学习目标】
1、探索三角形三边的关系,理解“三角形任何两边的和大于第三边”;
2、运用三角形的三边关系判断已知的三条线段能否组成三角形和,能根据三角形的两边,求第三边的取值范围.
3、理解三角形的稳定性,并能运用三角形的稳定性分析解决实际问题.
【学习重点和难点】
1、学习重点:理解运用三角形的三边关系;
2、学习难点:三角形三边关系的运用.
【学习过程】
一、知识回顾
1、 已知三角形的三边长为3、4、5,则这个三角形的周长是 .
2、 如图9.1-45,AD是△ABC的中线,△ABD的周长是25,
△ACD的周长是22,AC= 8,求AB的长度.
二、预习导学
1、画△ABC,使AB=7,AC=5,BC=4.
2、试一试:以下列长度的各组线段为边,能否画出一个三角形?按1的做法画一画,会得到怎样的图形?
(1) 7,4,2; (2)9,5,4.
想一想;(1)是不是任意三条线段都可以组成一个三角形?(2)什么情况下三条线段不能组成三角形?
3、概括:
(1)三角形三边关系: .
(2)三角形的稳定性: 三角形的三边固定,三角形的 和 就确定了,三角形的这个性质叫做三角形的稳定性.
三、预习检测
1、判断下列长度的各组线段能否组成一个三角形.
(1)15,18,7;( ) (2)5,6,12;( )
(3)13,7,6; ( ) (4)4,5,6. ( )
2、已知三角形的三边长为5,14,,则的取值范围是 .
3、等腰三角形的两边长为4,9,求这个三角形的周长.
四、典例分析
例1 三角形的三边长别为3,,,求的取值范围.
例2如图9.1-46,△ABC中,D是AB边上一点.
(1)求证:AB+BC+AC>2CD;
(2)求证:AB+2CD>AC+BC.
例3 已知等腰三角形的周长为24,一腰上的中线将它的周长分为5︰3两部分,求三角形三边的长.
五、分层练习
1、下列长度的三条线段能组成三角形的是( ).
A、1,2,3.5; B、4,4,9;
C、5,8,15; D、6,8,9.
2、现有四条线段的长度分别为4,6,8,10,从中任取三条线段,能组成三角形的个数为( ).
A、1个; B、2个; C、3个; D、4个.
3、如图,工人师傅在加工木门时,常用木条固定矩形门框,使其不变
形,工人师傅这样做的依据是 .
4、等腰三角形的两边长为7和5,则这个三角形的周长是 .
5、已知三角形三边长为,,,则的取值范围是 .
6、如图9.1-47,点O为△ABC内一点.
求证:AC+BC>AO+BO.
六、学习心得
七、课堂作业
八、家庭作业
九、课外延伸和拓展
1、已知一个三角形的两边长分别为和,其中,那么这个三角形的周长的取值范围是 .
2、等腰三角形的底边长为6,腰长为,则的取值范围是 .
3、已知、、是三角形的三边,试化简:.
4、等腰三角形一腰上的中线把这个三角形的周长分成12和15两部分,求这个三角形的腰长.
§9.2多边形的内角和与外角和
【学习目标】
1、了解多边形和正多边形;
2、探索多边形的内角和与外角和公式;
3、学会多边形内角和定理与外角和定理的应用.
【学习重点和难点】
探索和应用多边形的内角和与外角和公式
【学习过程】
一、知识回顾
1、三角形的内角和是 度?是怎样得来的?
2、三角形的外角和是 度?是怎样得来的?
二、预习导学
1、详细任务(在此作了任务了解,同时作为检验预习效果的标准):
(1)什么是三角形?那你能说出什么是四边形、五边形吗?
(2)三角形的内角和是 ?四边形 、五边形 ?
(3)三角形的外角和是 ?是怎样推导出来的?四边形 、五边形 ?
以上问题涉及到多边形的认识、多边形内角和与外角和定理的推导及其应用.这便是我们今天所要研究的内容.
2、多边形的认识:
(1)多边形的定义:三角形是最简单的多边形.正如三角形的定义一样,由 条不在同一直线上的 首尾顺次连结组成的平面图形称为边形,又称为多边形.如图:
(1) (2) (3)
图(1)的多边形记作四边形ABCD,图(2)的多边形记作 .
注:所有边相等、所有角也相等的多边形叫正多边形.如:正三角形(等边三角形)、正四边形(正方形)、正五边形……
(2)多边形的分类:
多边形 , 其中,凹多边形不是我们现在所研究的范围.
(3)多边形的组成:
边形有 条边, 个内角, 个外角.
2、多边形的内角和:
(1)对角线:
连结多边形不相邻两个顶点的线段叫多边形的对角线.如图(5),AC就是长方形ABCD的一条对角线,请画出它的另一条对角线.
(5) (6) (7)
试一试:(a)画出图(6)中五边形的所有对角线.
(b)你能推导出六边形有多少条对角线吗?画图验证.边形呢?
结论:边形的对角线条数为
从多边形的一个顶点引出的对角线可以把多边形分为若干个三角形.再问一下,从一下顶点出发能画出这样的对角线有多少条?
试一试:你能推导出从边形的一个顶点引出的对角线可以把边形分为多少个三角形吗?(再根据三角形内角和为180°,能否推出多边形的内角和公式?)
多边形边数 3 4 5 6 7 ……
分成的三角形个数 1 ……
多边形内角和 ……
(2)多边形内角和的推导(请你写出一个n边形的内角和公式的推导过程):
结论:边形的内角和为 .
注:正边形的每一个内角为 .
试一试:(a)十边形的内角和为 .
(b)如果一个多边形的内角和为2340°,则这个多边形的边数为 .
3、多边形的外角和:
(1)外角和的定义:与三角形的外角和一样,与多边形的每个内角相邻的外角有两个,这两个角是对顶角,从与每个内角相邻的两个外角中分别取一个相加, 得到的和称为多边形的外角和.
如图,∠1+∠2+∠3+∠4就是四边形ABCD的外角和.
那么这个和又是多少呢
(2)外角和的推导:(填表)
多边形的边数 3 4 5 6 7 ……
多边形内角与外角的总和
多边形的内角和
多边形的外角和
结论:多边形的外角和为 .
注:多边形的外角和与边数 .
正边形的每一个外角为 ;每一个内角为 .
三、归纳概括、理解记忆(把你认为重要的知识点概括在这个地方)
结论:
结论:
结论:
四、课堂检测:
1、P70课后练习1、2题;
2、填空:
(1)多边形的边数每增加1,内角和 ,外角和 .
(2)一个边形的内角和与外角和相等,则= .
(3)正十边形的每一个内角为 .
(4)若一个正边形的每一个外角都等于45°,则= .
(5)若一个正边形的每一个内角都等于120°,则= .
五、收获或疑问
六、能力提升:
1:一个多边形,除去一个内角外,其余各内角之和等于2500°,求这个多边形的边数.
2:一个八边形,现截去一个角,得到一个什么样的多边形,请求出得到的多边形的内角和与外角和.(提示:会不会有多种情况出现)
七、分层练习
A组
1、下列哪一个度数可以作为某一个多边形的内角和( )
A.240° B.600° C.540° D.2180°
2.六边形的外角和是( )
A.1080° B.720° C.540° D.360°
3.内角和等于外角和2倍的多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.一个多边形的每一个外角都是45°,则这个多边形的内角和为( )
A.360° B.1440° C.1080° D.720°
75过一个多边形的一个顶点可以引9条对角线,那么这个多边形的内角和是( )
A.1620° B.1800° C.1980° D.2160°
6.如果一个多边形的每个内角都等于144°,那么它的内角和为( ).
A、1260° B、1440° C、1620° D、1800°
二、填空
1.若一个多边形的每一个外角都是30°,则这个多边形的内角和等于______________度.
2.一个多边形的每个外角都相等,且比它的内角小140°,则个多边形是_____边形.
3.内角和与外角和相等的多边形是_____________边形.
4.若一个内角和与外角和的比试4:1,它的边数是_________,顶点个数是_________,对角线的条数是___________.
5.若一个四边形的四个内角度数之比为1:3:4:2,则这四个内角的度数分别是________.
三、解答题
1、一个多边形的每个内角都相等,都等于150°,求这个多边形的边数?(请用两种方法计算)
2、若两个多边形的内角和为1980°,两个多边形的边数之比为1︰2,求这两个多边形的边数.
B组
选择
1.若一个多边形有14条对角线,则这个多边形的边数是( )
A.10 B.7 C.14 D.6
2.一个多边形的内角和比他的外角和的3倍少180°,这个多边形的边数是( )
A.5 B.6 C.7 D.8
3.多边形的变数由3增加到n(n>3),其外角度数之和是( )
A.增加 B.保持不变 C.减小 D.变成(n-3) 180°
4.当多边形每增加一条边时,它的( )
A.外角和与内角和都增加180° B.外角和与内角和都增大180°
C.外角和增大180°,内角和不变 D.外角和不变,内角和增大180°
二、填空题
1.如图,分别以四边形ABCD的四个顶点为圆心,半径为R
作四个互不相交的圆,则图中阴影部分的面积之和是_____________.
2、一个边形的内角和小于1999度,那么的最大值是 .
3、如图,用同样规格的黑白两种正方形瓷砖铺设正方开地面,观察图形并猜想:当黑色瓷砖为20块时,白色瓷砖为 块;当白色瓷砖为块时,黑色瓷砖为 块.
三.解答题
1.如图,求∠A+∠B+∠C+∠D+∠E+∠F的值.
2.一个同学在进行多边形的内角和计算时,求的内角和为2750°,当发现错了之后,重新检查,发现少加了一个内角,问这个内角的度数是多少?求这个多边形的边数.
3、如图,在五边形ABCDE中,AE∥CD,∠A=130°,∠C=110°,求∠B的度数.
4、如图,∠1=∠2,∠A=135°,∠C=100°,求∠B的度数.
八、家庭作业
§9.3用正多边形拼地板
【学习目标】
1.通过用相同的正多边形拼地板活动,巩固多边形的内角和与外角和公式.
2.通过“拼地板”和有关计算,使学生从中发现能拼成一个不留空隙,又不重叠的平面图形的关键是平这个多边形的内角相加要等于 360°.
3.使学生进体会图形在日常生活中的应用.
【学习重点和难点】
1.重点:通过操作使学生发现能拼成一个平面图形的关键.
2.难点:同上.
【学习过程】
一、知识回顾
1、 ______________________________________________________叫正多边形.
2、正边形的内角和计算公式为________________.八边形的内角和为_______,每个内角均为_________度.
3、请完成下表:
二、预习导学
1、请自学课本P71-72页.并做一做,想一想以下问题.
2、用一种给定的正多边形,正方形、正五边形、正六边形、正七边形、正八边形,哪些正多边形可以密铺地面(也叫镶嵌)?为什么可以密铺?有什么规律?
3、请你自己亲自剪几个这样的正多边形试试?并且,把这些准备的正多边形带到学校,展示给同学看.
4、请自学课本P73页,回答下面的问题.
(1)试说明本节中几种正多边形铺满地面的理由.
图9.3.4
图9.3.5
图9.3.6
图9.3.7
(2)多边形中任取两种进行组合是否能铺满地面呢?
两种正多边形的类型 正方形、正三角形 正六边形、正三角形 正十二边形、正三角形
围绕一点每种正多边形的个数
围绕一点拼在一起的各角的度数和
(3)正十边形与正五方形能铺满地面吗?(提示:请利用本图,考虑是否能扩展到整个平面?)
结论:_________________________________________________.
三、归纳概括
1、怎样的一种正多边形可以实现铺满地面?
2、当 为正整数时,用这样的正n边形就可以铺满地面.(为什么,请推理)
3、怎样的多种正多边形可以实现铺满地面?
四、典例剖析
例1 某商店出售下列四种形状的地砖:
(1)正三角形;(2)正方形;(3)正五边形;(4)正六边形;(5)正八边形.
若只选购一种地砖镶嵌地面,可供选择的地砖有_____________________________.
例2 试画出用正三角形和正六边形铺满地面,但与图9.3.3不同的图形,你最多能有多少种方式?.
例3 请你尽可能多的列举只用一种正多边形能够铺满地面的多边形;用两种正多边形铺满地面的组合;列举用三种正多边形铺满地面的组合.
四、分层训练
A组
1、使用给定的某种一般三角形可以铺满地面吗?四边形呢?(不是正多边形哦)
2、现有四中地砖,形状分别是:正三角形、正方形、正六边形、正八边形,且它们边长都相等.同时选择其中两种地砖密铺地面,请问可行的组共 种,
分别是 .
3、现有正三角形、正十边形和第三种正多边形能铺满地板,则这第三种正多边形的边数是 .
B组
1、在一个城市的地图上,4个区的轮廓都是三角形形状.如果每个区与其他3个区都有公共边界,各区彼此的位置怎样?请画出示意图.
2.小红学习了用正多边形铺地板后做了这样的思考:教材上用一种正多边形拼地板,用两种也可以拼,用三种也可以拼,那么能否用四种正多边形拼地板呢?如果能,可选哪四种正多边形呢?请你帮小红同学解答这个问题.
五、收获或疑问:
六、家庭作业
C
B
A
O
D
E
图9.1-1
C
B
A
图9.1-2
C
B
A
图9.1-3
D
D
C
B
A
图9.1-4
B
E
C
F
A
D
图9.1-5
图9.1-6
B
D
C
A
1
图9.1-7
C
E
B
D
A
图9.1-8
C
E
B
D
A
图9.1-9
C
B
A
D
D
C
B
A
图9.1-10
……
图9.1-11
B
D
C
A
B
D
C
A
E
F
B
D
C
A
E
2
G
F
E
C
B
A
1
图9.1-13
·
A
B
P
A
B
O
B
D
C
A
1
B
E
C
A
2
B
F
C
A
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
1
B
D
C
A
2
F
E
G
H
图9.1-14
D
B
C
A
B
C
A
D
B
C
D
A
A
C
D
B
B
C
D
A
E
图9.1-15
B
C
A
D
图9.1-16
B
C
A
D
图9.1-17
F
B
C
A
E
图9.1-18
图9.1-19
C
E
B
D
A
F
图9.1-20
C
E
B
D
A
D
E
F
C
B
A
G
图9.1-21
D
B
C
A
C
B
A
M
E
O
D
F
图9.1-22
B
D
C
A
图9.1-23
B
D
A
C
图9.1-24
B
D
A
C
2
1
3
C
B
A
图9.1-26
E
B
C
A
D
图9.1-27
C
B
A
D
图9.1-28
B
C
A
O
图9.1-29
D
B
C
图9.1-30
A
D
E
B
C
图9.1-31
F
A
D
E
1
3
2
图9.1-32
C
E
B
H
A
D
图9.1-33
C
E
B
F
A
D
1
2
图9.1-34
D
C
B
A
B
D
C
A
图9.1-36
D
E
C
B
A
图9.1-37
图9.1-38
B
C
A
1
2
N
M
图9.1-39
E
C
B
A
D
图9.1-40
C
B
A
D
图9.1-41
D
C
B
A
图9.1-42
E
B
A
D
Q
P
C
F
O
图9.1-43
C
B
A
D
图9.1-44
C
E
D
B
A
图9.1-45
B
D
C
A
图9.1-46
A
D
B
C
图9.1-47
A
O
B
C
A
E
D
C
B
A
B
D
C
A
B
C
D
A
D
C
B
你还有没有其他证明方法?看看P70图9.2.5。聪明的你,若有新方法,请你把你的想法写在这里。(不只一种哦)
A
B
D
C
1
2
3
4
回忆三角形外角和的推导过程,想一想,与你的伙伴交流交流.
第1题图
A
B
C
D
E
F
第1题图
C
B
A
E
D
1
D
B
C
A
M
E
N
2
第九章 《多边形》导学案 第25页
第一课时
【学习内容】
§9.1.1 认识三角形(1)
【学习目标】
1、了解三角形、三角形的边、顶点、内角、外角等概念;会准确地表示三角形及其边、角.
2、能按角、边分别将三角形分类;
3、理解等腰三角形、等边三角形的概念.
【学习重点和难点】
1、学习重点:三角形内角、外角、等腰三角形、等边三角形等概念;
2、学习难点:三角形的外角.
【学习过程】
一、知识回顾
1、回顾线段、射线、直线相关知识,填写下表:
名称 特征 延伸性 端点个数 表示方法 性质
线段
直线
射线
2、由 组成的图形叫做角,角也可以看成是
的图形.射线的端点叫做角的顶点,起始位置的射线叫做角的始边,终止位置的射线叫做角的终边.
3、如图9.1-1,图中一共有 个小于平角的角,它们分
别是
.
二、预习导学
1、三角形的定义:三角形是由 组成的平面图形.
三角形的表示符号为“△”,通常是在“△”后面加上
三顶点的字母来表示三角形. 如图9.1-2,图中的三角形应
记作 .
2、三角形的顶点:三角形中,相邻两条线段的 ,
叫做三角形的顶点,通常用一个大写字母表示,每个三角形有三个顶点.
3、三角形的边: . 每个三角形有 条边.
4、三角形的内角: . 每个三角形有 个内角.
5、三角形的外角: .
如图9.1-3,∠ACD是△ABC的一个外角,它是△ABC的
内角∠ 的 边与 边的反向延长线所组成的角.
思考:还能画出与∠ACB相邻的外角吗?它与∠ACD有怎
样的关系?△ABC一共有多个外角?
6、三角形的分类:
(1)按角分:三角形
(2)按边分:三角形
三、预习检测
1、认真读图9.1-4,解答下列各题.
(1)图中有 个三角形,它们分别是
;
(2)△ACD的三边分别是 ,
三个内角分别是 ,它的外角是 .
(3)∠ACB是△ 的内角,它的对边是 ,∠ACD是△ 的外角.
BD是△ 的边,它的对角是 .
2、如图9.1-5,图中以BC为边的三角形共有 个;
它们分别 .
在△ABD中,∠A是 边的对角, ∠ADB是
△ 的内角,又是 的一个外角.
四、典例剖析
例1 如图9.1-6,图中的三角形可以表示为 ,
它的三边分别是 ,它的三个内角分别
是 、 、 ;与∠1的相邻的外
角是 ,∠1+∠BCD = .
例2 下列关于等腰三角形的说法正确的有 .
(1)有且只有两条边相等的三角形是等腰三角形;(2)有两条边相等的三角形是等腰三角形;(3)等腰三角形都是锐角三角形;(4)三角形可分为不等边三角形、等腰三角形、等边三角形.
例3 在△ABC中,∠A=∠B=∠C,试判断△ABC的形状.
五、分层练习
1、如图9.1-7,∠B是 的内角,
△ABD的外角是 ; 在△ABE中,AE所对的角是
;在△ADE中AD是 的对边,在△ADC
中AD是 的对边.
2、若有一条公共边的两个三角形称为一对“共边三角形”,在图9.1-8中,以BC为公共边的“共边三角形” 有 .
3、如图9.1-9,在△ABC中,∠ACB是钝角,让点C在射线
BD上向右移动,则下列说法正确的是( ).
A、△ABC将变为锐角三角形,不再变为钝角三角形;
B、△ABC将先变为直角三角形,然后变为锐角三角形,而
再不会是钝角三角形;
C、△ABC将先变为直角三角形,然后变为锐角三角形,接
着又由锐角三角形变为钝角三角形;
D、△ABC先由钝角三角形变为直角三角形,再变为锐角三
角形,接着又变为直角三角形,然后再次变为钝角三角形.
4、若三角形的一个外角为115°,则与这个外角相邻的内角等于 °;若一个三角形的一个外角等于它相邻内角的2倍,则这个外角的度数是 °.
5、已知,三角形的三边的比是3︰4︰5,且最大边长与最小边长的差是4,求这个三角形的三条边的长.
6、如图9.1-10,在△ABC中,∠ACB=90°,CD⊥AB于D,AB=10,AC=8,BC=6.
(1)求△ABC的面积;(2)求高CD的长.
六、学习心得
七、课堂作业
八、家庭作业
九、课外延伸和拓展
1、如图9.1-11,观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有 个.
第1个 第2个 第3个
2、如图9.1-12,已知△ABC.
(1)△ABC中有一条线段AD时,共有 个三角形;
(2)△ABC中有两条线段AD、AE时,共有 个三角形;
(3)△ABC中有三条线段AD、AE、AF时,共有 个三角形;
(4)△ABC中有10条这样的线段时,共有 个三角形;
(5)△ABC中有条这样的线段时,共有 个三角形.
……
(1) (2) (3)
图9.1-12
§9.1 三角形
第二课时
【学习内容】
§9.1.1 认识三角形(2)
【学习目标】
1、掌握三角形的角平分线、中线、高的概念.
2、会画出任意三角形的角平分线、中线、高;
3、能运用三角形的角平分线、中线、高的定义解决一些简单的问题.
【学习重点和难点】
1、学习重点:三角形角平分线、中线、高的概念及其画法;
2、学习难点:钝角三角形高的画法.
【学习过程】
一、知识回顾
1、如图9.1-13,图中共有 个三角形,其中以BC为
一边的三角形有 ;
以∠1为内角的三角形是 ;
以∠2为外角的三角形是 .
2、在下列条件中,能判定△ABC是直角三形的是 .
(1)∠A+∠B=90°; (2)∠A︰∠B︰∠C=1︰2︰3; (3)∠A= 90°-∠B;
(4)∠A=∠B=∠C; (5)∠A=2∠B=3∠C. (6)AC⊥BC于点C.
3、(1)已知∠AOB,作∠AOB的平分线OC; (2)已知直线AB外一点P,过点P作PC⊥AB于点C.
二、预习导学
1、三角形的中线:三角形的 与 的连线叫三角形的中线.
(1)三角形中线的判定:
∵ 点D是BC边的中点(BD=CD)
∴
(2)三角形中线的性质:
∵AD是△ABC的中线
∴
2、三角形的角平分线:三角形 与 之间的线段叫三角形的角平分线.
(1)三角形角平分线的判定:
∵∠1=∠2
∴
(2)三角形角平分线的性质:
∵ CE是△ABC的角平分线
∴
3、三角形的高:过三角形顶点作对边的垂线, 与 之间的线段叫三角形的高.
(1)三角形高的判定:
∵BF⊥AC于点F
∴
(2)三角形高的性质:
∵BF是△ABC的高
∴
4、做一做:
(1)分别画出锐角△ABC的中线、角平分线和高.
作出中线 作出角平分线 作出高
(2)分别画出直角△ABC的中线、角平分线和高.
作出中线 作出角平分线 作出高
(3)分别画出钝角△ABC的中线、角平分线和高.
作出中线 作出角平分线 作出高
我的发现:
(1)三角形有 条中线; 条角平分线; 条高.
(2)三角形的中线、角平分线、高都是 ,一个端点是三角形的 ,另一个端点在 .
(3)任意三角形的三条中线都在三角形的 ,并交于 .
(4)任意三角形的三条角平分线都在三角形的 ,并交于 .
(5)锐角三角形的三条高都在三角形的 ,并交于 .
直角三角形的斜边上的高在三角形的 ,另两条高恰好是 ,三条高交于 .
钝角三角形的最大边上的高在三角形的 ,另两条高在三角形的 ,三条高交于 .
三、预习检测
1、如图9.1-14,在△ABC中,∠1=∠2,G为AD中点,延长
BG交AC于E,F为AB上一点,CF⊥AD于H,下列说法
正确的是 .
① AD是△ABE的角平分线;② BE是△ABD边AD上的中线;
③ BE是△ABC边AC上的中线;④ CH是△ACD边AD上的高.
2、如图△ABC,画边BC上的高,下面的画法正确吗?若不正确,请画出正确的高.
(1) (2) (3) (4)
3、如图9.1-15,AD⊥BC于D,以AD为高的
三角形有 .
四、典例剖析
例1 如图9.1-16,AD是△ABC的中线,AB=5,AC=3.
(1)求△ABD与△ADC的周长相差多少?
(2)猜想△ABD与△ADC的面积有怎样的关系,
并证明你的猜想.
例2 如图9.1-17,在△ABC中,∠A=80°,BD、CD分别平分∠ABC、∠ACB.
求∠BDC的度数.
例3 如图9.1-18,在△ABC中AE是∠BAC的平分线,
AF是BC边上的高,∠B=35°,∠C=65°.
求∠EAF的度数.
五、分层练习
1、下列说法中正确的是( ).
A、三角形的中线就是过顶点平分对边的直线;
B、三角形的高就是顶点到对边的距离;
C、三角形的角分线就是三角形的内角的平分线
D、三角形的三条中线必交于一点.
2、三角形一边上的中线把原三角形分成两个( ).
A、形状相同的三角形; B、面积相等的三角形;
C、直角三角形; D、周长相等的三角形.
3、如图9-1-19,BD=DE=EF=CF,图中共有 个三角形,
AF是△ 的中线,AE是△ 的中线.
4、如图9.1-20,已知AC⊥BC,CD⊥AB,DE⊥BC,则在△ABC中, 是BC边上的高;△BCD中, 是BC边上的高;△ABE中, 是BE边上的高;△ACD中, 是CD边上的高.
5、如图9.1-21,△ABC的三条角平分线交于一点G,∠BAC=76°,∠ABE=20°.
求∠BEC、∠ADC、∠DGC的度数.
六、学习心得
七、课堂作业
八、家庭作业
九、课外延伸和拓展
1、如图,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm,
AB=5cm,CD是AB边上的高,求CD的长度.
2、在等腰△ABC中,AB=AC,一腰上的中线将这个等腰三角形的周长分这21和12两部分,求△ABC的腰长和底边长.
3、如图,点O是等边三角形内任意一点,OD⊥AB,
OE⊥BC,OF⊥AC,高AM⊥BC.
试说明OD+OE+OF=AM.
§9.1 三角形
第三课时
【学习内容】
§9.1.2 三角形的外角和(1)
【学习目标】
1、探索并掌握三角形外角的性质、三角形的外角和定理;
2、能运用平行线等知识证明三角形外角的性质1、三角形的外角和是360°;
3、能运用三角形外角的性质、三角形的外角和定理进行简单的计算和说理.
【学习重点和难点】
1、学习重点:三角形外角的性质、三角形外角和定理;
2、学习难点:运用三角形外角的性质、三角形外角和定理进行简单的计算和说理.
【学习过程】
一、知识回顾
1、什么叫三角形?三角形的内角?三形的外角?
2、三角形的内角和定理: .
3、如图9.1-22,点D是△ABC的BC边上一点,已知∠BAD=35°,
∠B=45°,则∠ADB= °,∠ADC= °.
二、预习导学
1、一个三角形的每一个外角对应一个 的内角
和两个 的内角.
如图9.1-23,∠CBD是△ABC的一个外角,与∠CBD相邻的
内角是 ,与∠CBD不相邻的内角是 .
∠CBD+∠ABC= °.
2、三角形外角的性质
(1)三角形的一个外角等于 的两个内角的和.
(2)三角形的一个外角大于任何一个 的内角.
如图9.1-24,∠CBD是△ABC的一个外角.
求证:∠CBD=∠A+∠C.
3、与三角形的每个内角相邻的外角分别有两个,这两个外角是 ;从与每个内角相邻的两个外角中分别取一个相加,得到的和叫做 .
4、三角形的外角和定理: .
如图9.1-25,∠1、∠2、∠3分别是△ABC的外角.
求证:∠1+∠2+∠3=360°.
想一想:
你还有别的方法可以证明∠1+∠2+∠3=360°吗?试结合图9.1-26写出你的证明过程.
三、预习检测
1、求下列各图中∠1的度数.
解:(1)∠1= °; (2)∠1= °; (3)∠1= °.
2、如图9.1-27,在△ABC中,∠A=35°,∠CBD=115°.
求∠BCE的度数.
四、典例剖析
例1 如图9.1-28,点D是△ABC的BC边上一点,
∠C=∠CAD,∠ADB=70°,∠BAC=80°.
求∠B的度数.
例2 如图9.1-29,∠A=56°,∠ABD=20°,∠ACO=32°.
求∠BOC的度数.
例3 如图9.1-30,△ABC的外角∠ACE的平分线交BA延长线于点D.
证明:∠BAC>∠B.
五、分层练习
1、下列说法错误的是( ).
A、一个三角表中至少有一个角不大于60°;
B、三角形的一个外角等于与它不相邻的两个内角的和;
C、三角形的一个外角大于它的一个内角.
D、若一个三角形的一个角的外角与它相邻的内角相等,那
么这个三角形是直角三角形;
2、如图9.1-31,在△ABC中,点D是BC延长线上一点,
点F是AB边上一点,延长CA到E,连结EF.
则∠1、∠2、∠3的大小关系是 .
3、如图9.1-32,在△ABC中,∠A=60°,BD、CE分别是AC、AB边上的高,H是BD、CE的交点,求∠BHC的度数.
六、学习心得
七、课堂作业
八、家庭作业
九、课外延伸和拓展
1、如图9.1-33,已知∠1=∠2,∠BAC=70°,求∠DEF度数.
2、如图9.1-34,求证:∠D>∠A.
§9.1 三角形
第四课时
【学习内容】
§9.1.2 三角形的外角和(2)
【学习目标】
1、复习巩固三角形的外角的性质、三角形的外角和定理;
3、能熟练地运用三角形外角的性质、三角形的外角和进行计算和说理.
【学习重点和难点】
1、学习重点:三角形外角的性质、三角形外角和定理的应用;
2、学习难点:灵活运用三角形的外角性质和外角和定理.
【学习过程】
一、知识回顾
1、三角形的外角和定理:在三角形的每一个顶点取一个外角,所得的和是三角形的外角和,三角形的外角和等于 .
2、三角形外角的性质
(1)三角形的一个外角等于 .
(2)三角形的一个内角大于 .
3、如图9.1-36,在△ABC中,AD平分∠BAC,∠B=50°,∠C=68°.
求∠ADC的度数.
二、典例剖析
例1 如图9.1-37,AE是△ABC的外角∠CAD的角平分线,∠B=35°,∠EAD=60°.
求∠ACE的度数.
例2 如图9.1-38,在△ABC中,∠C=50°,若沿图中虚线MN剪去∠C.
求∠1+∠2的度数.
例3 如图9.1-39,五角星ABCDE中,求∠A+∠B+∠C+∠D+∠E的度数.
三、分层练习
1、 如图9.1-40,∠CAD=120°,∠C=40°,则∠B= °.
2、 在△ABC中,∠A、∠B、∠C相邻外角的比是2︰3︰4,
则∠A= °,∠B= °,∠C= °.
3、 在△ABC中,与∠C相邻的外角是120°,∠A的度数是∠B的度
数的.求△ABC各内角的度数.
4、 如图9.1-41,∠A=50°,∠B=35°∠C=25°.
求∠BDC的度数.
5、 如图9.1-42,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
四、学习心得
五、课堂作业
六、家庭作业
七、课外延伸和拓展
1、 一个零件的形状如图9.1-43所示,按规定∠A=90°,∠B=30°,∠D=20°. 李师傅量得∠BCD=142°,就断定这个零件不合格.
李师傅的说法正确吗?请说明理由.
2、如图9.1-44,在△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=80°,∠C=40°,求∠DAE的度数.
(2)若∠B -∠C= 40°,你能求出∠DAE的度数吗?
如果能,请求出∠DAE的度数.
(3)通过(1)、(2)的计算,请写出∠DAE与∠B、
∠C之间的关系.
§9.1 三角形
第五课时
【学习内容】
§9.1.3 三角形的三边关系
【学习目标】
1、探索三角形三边的关系,理解“三角形任何两边的和大于第三边”;
2、运用三角形的三边关系判断已知的三条线段能否组成三角形和,能根据三角形的两边,求第三边的取值范围.
3、理解三角形的稳定性,并能运用三角形的稳定性分析解决实际问题.
【学习重点和难点】
1、学习重点:理解运用三角形的三边关系;
2、学习难点:三角形三边关系的运用.
【学习过程】
一、知识回顾
1、 已知三角形的三边长为3、4、5,则这个三角形的周长是 .
2、 如图9.1-45,AD是△ABC的中线,△ABD的周长是25,
△ACD的周长是22,AC= 8,求AB的长度.
二、预习导学
1、画△ABC,使AB=7,AC=5,BC=4.
2、试一试:以下列长度的各组线段为边,能否画出一个三角形?按1的做法画一画,会得到怎样的图形?
(1) 7,4,2; (2)9,5,4.
想一想;(1)是不是任意三条线段都可以组成一个三角形?(2)什么情况下三条线段不能组成三角形?
3、概括:
(1)三角形三边关系: .
(2)三角形的稳定性: 三角形的三边固定,三角形的 和 就确定了,三角形的这个性质叫做三角形的稳定性.
三、预习检测
1、判断下列长度的各组线段能否组成一个三角形.
(1)15,18,7;( ) (2)5,6,12;( )
(3)13,7,6; ( ) (4)4,5,6. ( )
2、已知三角形的三边长为5,14,,则的取值范围是 .
3、等腰三角形的两边长为4,9,求这个三角形的周长.
四、典例分析
例1 三角形的三边长别为3,,,求的取值范围.
例2如图9.1-46,△ABC中,D是AB边上一点.
(1)求证:AB+BC+AC>2CD;
(2)求证:AB+2CD>AC+BC.
例3 已知等腰三角形的周长为24,一腰上的中线将它的周长分为5︰3两部分,求三角形三边的长.
五、分层练习
1、下列长度的三条线段能组成三角形的是( ).
A、1,2,3.5; B、4,4,9;
C、5,8,15; D、6,8,9.
2、现有四条线段的长度分别为4,6,8,10,从中任取三条线段,能组成三角形的个数为( ).
A、1个; B、2个; C、3个; D、4个.
3、如图,工人师傅在加工木门时,常用木条固定矩形门框,使其不变
形,工人师傅这样做的依据是 .
4、等腰三角形的两边长为7和5,则这个三角形的周长是 .
5、已知三角形三边长为,,,则的取值范围是 .
6、如图9.1-47,点O为△ABC内一点.
求证:AC+BC>AO+BO.
六、学习心得
七、课堂作业
八、家庭作业
九、课外延伸和拓展
1、已知一个三角形的两边长分别为和,其中,那么这个三角形的周长的取值范围是 .
2、等腰三角形的底边长为6,腰长为,则的取值范围是 .
3、已知、、是三角形的三边,试化简:.
4、等腰三角形一腰上的中线把这个三角形的周长分成12和15两部分,求这个三角形的腰长.
§9.2多边形的内角和与外角和
【学习目标】
1、了解多边形和正多边形;
2、探索多边形的内角和与外角和公式;
3、学会多边形内角和定理与外角和定理的应用.
【学习重点和难点】
探索和应用多边形的内角和与外角和公式
【学习过程】
一、知识回顾
1、三角形的内角和是 度?是怎样得来的?
2、三角形的外角和是 度?是怎样得来的?
二、预习导学
1、详细任务(在此作了任务了解,同时作为检验预习效果的标准):
(1)什么是三角形?那你能说出什么是四边形、五边形吗?
(2)三角形的内角和是 ?四边形 、五边形 ?
(3)三角形的外角和是 ?是怎样推导出来的?四边形 、五边形 ?
以上问题涉及到多边形的认识、多边形内角和与外角和定理的推导及其应用.这便是我们今天所要研究的内容.
2、多边形的认识:
(1)多边形的定义:三角形是最简单的多边形.正如三角形的定义一样,由 条不在同一直线上的 首尾顺次连结组成的平面图形称为边形,又称为多边形.如图:
(1) (2) (3)
图(1)的多边形记作四边形ABCD,图(2)的多边形记作 .
注:所有边相等、所有角也相等的多边形叫正多边形.如:正三角形(等边三角形)、正四边形(正方形)、正五边形……
(2)多边形的分类:
多边形 , 其中,凹多边形不是我们现在所研究的范围.
(3)多边形的组成:
边形有 条边, 个内角, 个外角.
2、多边形的内角和:
(1)对角线:
连结多边形不相邻两个顶点的线段叫多边形的对角线.如图(5),AC就是长方形ABCD的一条对角线,请画出它的另一条对角线.
(5) (6) (7)
试一试:(a)画出图(6)中五边形的所有对角线.
(b)你能推导出六边形有多少条对角线吗?画图验证.边形呢?
结论:边形的对角线条数为
从多边形的一个顶点引出的对角线可以把多边形分为若干个三角形.再问一下,从一下顶点出发能画出这样的对角线有多少条?
试一试:你能推导出从边形的一个顶点引出的对角线可以把边形分为多少个三角形吗?(再根据三角形内角和为180°,能否推出多边形的内角和公式?)
多边形边数 3 4 5 6 7 ……
分成的三角形个数 1 ……
多边形内角和 ……
(2)多边形内角和的推导(请你写出一个n边形的内角和公式的推导过程):
结论:边形的内角和为 .
注:正边形的每一个内角为 .
试一试:(a)十边形的内角和为 .
(b)如果一个多边形的内角和为2340°,则这个多边形的边数为 .
3、多边形的外角和:
(1)外角和的定义:与三角形的外角和一样,与多边形的每个内角相邻的外角有两个,这两个角是对顶角,从与每个内角相邻的两个外角中分别取一个相加, 得到的和称为多边形的外角和.
如图,∠1+∠2+∠3+∠4就是四边形ABCD的外角和.
那么这个和又是多少呢
(2)外角和的推导:(填表)
多边形的边数 3 4 5 6 7 ……
多边形内角与外角的总和
多边形的内角和
多边形的外角和
结论:多边形的外角和为 .
注:多边形的外角和与边数 .
正边形的每一个外角为 ;每一个内角为 .
三、归纳概括、理解记忆(把你认为重要的知识点概括在这个地方)
结论:
结论:
结论:
四、课堂检测:
1、P70课后练习1、2题;
2、填空:
(1)多边形的边数每增加1,内角和 ,外角和 .
(2)一个边形的内角和与外角和相等,则= .
(3)正十边形的每一个内角为 .
(4)若一个正边形的每一个外角都等于45°,则= .
(5)若一个正边形的每一个内角都等于120°,则= .
五、收获或疑问
六、能力提升:
1:一个多边形,除去一个内角外,其余各内角之和等于2500°,求这个多边形的边数.
2:一个八边形,现截去一个角,得到一个什么样的多边形,请求出得到的多边形的内角和与外角和.(提示:会不会有多种情况出现)
七、分层练习
A组
1、下列哪一个度数可以作为某一个多边形的内角和( )
A.240° B.600° C.540° D.2180°
2.六边形的外角和是( )
A.1080° B.720° C.540° D.360°
3.内角和等于外角和2倍的多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.一个多边形的每一个外角都是45°,则这个多边形的内角和为( )
A.360° B.1440° C.1080° D.720°
75过一个多边形的一个顶点可以引9条对角线,那么这个多边形的内角和是( )
A.1620° B.1800° C.1980° D.2160°
6.如果一个多边形的每个内角都等于144°,那么它的内角和为( ).
A、1260° B、1440° C、1620° D、1800°
二、填空
1.若一个多边形的每一个外角都是30°,则这个多边形的内角和等于______________度.
2.一个多边形的每个外角都相等,且比它的内角小140°,则个多边形是_____边形.
3.内角和与外角和相等的多边形是_____________边形.
4.若一个内角和与外角和的比试4:1,它的边数是_________,顶点个数是_________,对角线的条数是___________.
5.若一个四边形的四个内角度数之比为1:3:4:2,则这四个内角的度数分别是________.
三、解答题
1、一个多边形的每个内角都相等,都等于150°,求这个多边形的边数?(请用两种方法计算)
2、若两个多边形的内角和为1980°,两个多边形的边数之比为1︰2,求这两个多边形的边数.
B组
选择
1.若一个多边形有14条对角线,则这个多边形的边数是( )
A.10 B.7 C.14 D.6
2.一个多边形的内角和比他的外角和的3倍少180°,这个多边形的边数是( )
A.5 B.6 C.7 D.8
3.多边形的变数由3增加到n(n>3),其外角度数之和是( )
A.增加 B.保持不变 C.减小 D.变成(n-3) 180°
4.当多边形每增加一条边时,它的( )
A.外角和与内角和都增加180° B.外角和与内角和都增大180°
C.外角和增大180°,内角和不变 D.外角和不变,内角和增大180°
二、填空题
1.如图,分别以四边形ABCD的四个顶点为圆心,半径为R
作四个互不相交的圆,则图中阴影部分的面积之和是_____________.
2、一个边形的内角和小于1999度,那么的最大值是 .
3、如图,用同样规格的黑白两种正方形瓷砖铺设正方开地面,观察图形并猜想:当黑色瓷砖为20块时,白色瓷砖为 块;当白色瓷砖为块时,黑色瓷砖为 块.
三.解答题
1.如图,求∠A+∠B+∠C+∠D+∠E+∠F的值.
2.一个同学在进行多边形的内角和计算时,求的内角和为2750°,当发现错了之后,重新检查,发现少加了一个内角,问这个内角的度数是多少?求这个多边形的边数.
3、如图,在五边形ABCDE中,AE∥CD,∠A=130°,∠C=110°,求∠B的度数.
4、如图,∠1=∠2,∠A=135°,∠C=100°,求∠B的度数.
八、家庭作业
§9.3用正多边形拼地板
【学习目标】
1.通过用相同的正多边形拼地板活动,巩固多边形的内角和与外角和公式.
2.通过“拼地板”和有关计算,使学生从中发现能拼成一个不留空隙,又不重叠的平面图形的关键是平这个多边形的内角相加要等于 360°.
3.使学生进体会图形在日常生活中的应用.
【学习重点和难点】
1.重点:通过操作使学生发现能拼成一个平面图形的关键.
2.难点:同上.
【学习过程】
一、知识回顾
1、 ______________________________________________________叫正多边形.
2、正边形的内角和计算公式为________________.八边形的内角和为_______,每个内角均为_________度.
3、请完成下表:
二、预习导学
1、请自学课本P71-72页.并做一做,想一想以下问题.
2、用一种给定的正多边形,正方形、正五边形、正六边形、正七边形、正八边形,哪些正多边形可以密铺地面(也叫镶嵌)?为什么可以密铺?有什么规律?
3、请你自己亲自剪几个这样的正多边形试试?并且,把这些准备的正多边形带到学校,展示给同学看.
4、请自学课本P73页,回答下面的问题.
(1)试说明本节中几种正多边形铺满地面的理由.
图9.3.4
图9.3.5
图9.3.6
图9.3.7
(2)多边形中任取两种进行组合是否能铺满地面呢?
两种正多边形的类型 正方形、正三角形 正六边形、正三角形 正十二边形、正三角形
围绕一点每种正多边形的个数
围绕一点拼在一起的各角的度数和
(3)正十边形与正五方形能铺满地面吗?(提示:请利用本图,考虑是否能扩展到整个平面?)
结论:_________________________________________________.
三、归纳概括
1、怎样的一种正多边形可以实现铺满地面?
2、当 为正整数时,用这样的正n边形就可以铺满地面.(为什么,请推理)
3、怎样的多种正多边形可以实现铺满地面?
四、典例剖析
例1 某商店出售下列四种形状的地砖:
(1)正三角形;(2)正方形;(3)正五边形;(4)正六边形;(5)正八边形.
若只选购一种地砖镶嵌地面,可供选择的地砖有_____________________________.
例2 试画出用正三角形和正六边形铺满地面,但与图9.3.3不同的图形,你最多能有多少种方式?.
例3 请你尽可能多的列举只用一种正多边形能够铺满地面的多边形;用两种正多边形铺满地面的组合;列举用三种正多边形铺满地面的组合.
四、分层训练
A组
1、使用给定的某种一般三角形可以铺满地面吗?四边形呢?(不是正多边形哦)
2、现有四中地砖,形状分别是:正三角形、正方形、正六边形、正八边形,且它们边长都相等.同时选择其中两种地砖密铺地面,请问可行的组共 种,
分别是 .
3、现有正三角形、正十边形和第三种正多边形能铺满地板,则这第三种正多边形的边数是 .
B组
1、在一个城市的地图上,4个区的轮廓都是三角形形状.如果每个区与其他3个区都有公共边界,各区彼此的位置怎样?请画出示意图.
2.小红学习了用正多边形铺地板后做了这样的思考:教材上用一种正多边形拼地板,用两种也可以拼,用三种也可以拼,那么能否用四种正多边形拼地板呢?如果能,可选哪四种正多边形呢?请你帮小红同学解答这个问题.
五、收获或疑问:
六、家庭作业
C
B
A
O
D
E
图9.1-1
C
B
A
图9.1-2
C
B
A
图9.1-3
D
D
C
B
A
图9.1-4
B
E
C
F
A
D
图9.1-5
图9.1-6
B
D
C
A
1
图9.1-7
C
E
B
D
A
图9.1-8
C
E
B
D
A
图9.1-9
C
B
A
D
D
C
B
A
图9.1-10
……
图9.1-11
B
D
C
A
B
D
C
A
E
F
B
D
C
A
E
2
G
F
E
C
B
A
1
图9.1-13
·
A
B
P
A
B
O
B
D
C
A
1
B
E
C
A
2
B
F
C
A
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
1
B
D
C
A
2
F
E
G
H
图9.1-14
D
B
C
A
B
C
A
D
B
C
D
A
A
C
D
B
B
C
D
A
E
图9.1-15
B
C
A
D
图9.1-16
B
C
A
D
图9.1-17
F
B
C
A
E
图9.1-18
图9.1-19
C
E
B
D
A
F
图9.1-20
C
E
B
D
A
D
E
F
C
B
A
G
图9.1-21
D
B
C
A
C
B
A
M
E
O
D
F
图9.1-22
B
D
C
A
图9.1-23
B
D
A
C
图9.1-24
B
D
A
C
2
1
3
C
B
A
图9.1-26
E
B
C
A
D
图9.1-27
C
B
A
D
图9.1-28
B
C
A
O
图9.1-29
D
B
C
图9.1-30
A
D
E
B
C
图9.1-31
F
A
D
E
1
3
2
图9.1-32
C
E
B
H
A
D
图9.1-33
C
E
B
F
A
D
1
2
图9.1-34
D
C
B
A
B
D
C
A
图9.1-36
D
E
C
B
A
图9.1-37
图9.1-38
B
C
A
1
2
N
M
图9.1-39
E
C
B
A
D
图9.1-40
C
B
A
D
图9.1-41
D
C
B
A
图9.1-42
E
B
A
D
Q
P
C
F
O
图9.1-43
C
B
A
D
图9.1-44
C
E
D
B
A
图9.1-45
B
D
C
A
图9.1-46
A
D
B
C
图9.1-47
A
O
B
C
A
E
D
C
B
A
B
D
C
A
B
C
D
A
D
C
B
你还有没有其他证明方法?看看P70图9.2.5。聪明的你,若有新方法,请你把你的想法写在这里。(不只一种哦)
A
B
D
C
1
2
3
4
回忆三角形外角和的推导过程,想一想,与你的伙伴交流交流.
第1题图
A
B
C
D
E
F
第1题图
C
B
A
E
D
1
D
B
C
A
M
E
N
2
第九章 《多边形》导学案 第25页
