2021-2022学年鲁教版(五四制)六年级数学上册3.7探索与表达规律 同步优生辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级数学上册3.7探索与表达规律 同步优生辅导训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 203.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 11:56:18 | ||
图片预览



文档简介
2021-2022学年鲁教版六年级数学上册《3.7探索与表达规律》同步优生辅导训练(附答案)
一.规律型:数字的变化类
1.按一定规律排列的一列数为,2,,8,,18…,则第8个数为 ,第n个数为 .
2.古希腊毕达格拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数,比如:他们研究过图1中的1,3,6,10,….由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…,这样的数为正方形数.
(1)请你写出一个既是三角形数又是正方形数的自然数 .
(2)类似地,我们将k边形数中第n个数记为N(n,k)(k≥3).以下列出了部分k边形数中第n个数的表达式:
三角形数:N(n,3)=n2+n
正方形数:N(n,4)=n2
五边形数:N(n,5)=n2﹣n
六边形数:N(n,6)=2n2﹣n…
根据以上信息,得出N(n,k)= .(用含有n和k的代数式表示)
3.如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
(1)表中第9行第7个数是 ;
(2)2020是表中第 行第 个数.
4.一组按一定规律排列的式子:,…,(a≠0)则第n个式子是 .
5.观察下列各等式:
第一个等式:=1,第二个等式:=2,第三个等式:=3…
根据上述等式反映出的规律直接写出第四个等式为 ;猜想第n个等式(用含n的代数式表示)为 .
6.观察下列按照一定规律写出的各行的数:
第1行:1,1;
第2行:1,2,1;
第3行:1,3,3,1;
第4行:1,4,6,4,1;
….
(1)按照上面的规律写下去,请你写出第5行的这列数 ;
(2)第n行的所有数的和是 (用含n的式子表示).
7.小明在一本书中发现了下面三个奇怪的等式:;;
他一一检验后发现它们都是正确的.小明想除了上述三个之外应该还有这样奇怪的式子,于是小明进一步研究,不但写出了很多这样奇怪的等式,还找到了内在的规律:如果一个数为,另一个数为 时(用a,b表示),可以构成类似上述的奇怪等式.
8.把正整数1,2,3,4,5,…,按如下规律排列:
1
2,3,
4,5,6,7,
8,9,10,11,12,13,14,15,
…
按此规律,可知第n行有 个正整数.
9.仔细观察下列三组数:
第一组:1,﹣4,9,﹣16,25,…
第二组:﹣1,8,﹣27,64,﹣125,…
第三组:﹣2,﹣8,﹣18,﹣32,﹣50,…
(1)第一组的第6个数是 ;
(2)第二组的第n个数是 ;
(3)分别取每一组的第10个数,计算这三个数的和.
10.由于(﹣1)n=,所以我们通常把(﹣1)n称为符号系数.
(1)观察下列单项式:﹣,…按此规律,第5个单项式是 ,第n个单项式是 .
(2)的值为 ;
(3)你根据(2)写出一个当n为偶数时值为2,当n为奇数时值为0的式子 .
11.观察以下等式:
第1个等式:++×=1,
第2个等式:++×=1,
第3个等式:++×=1,
第4个等式:++×=1,
第5个等式:++×=1,
……
按照以上规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第n个等式: (用含n的等式表示),并证明.
二.规律型:图形的变化类
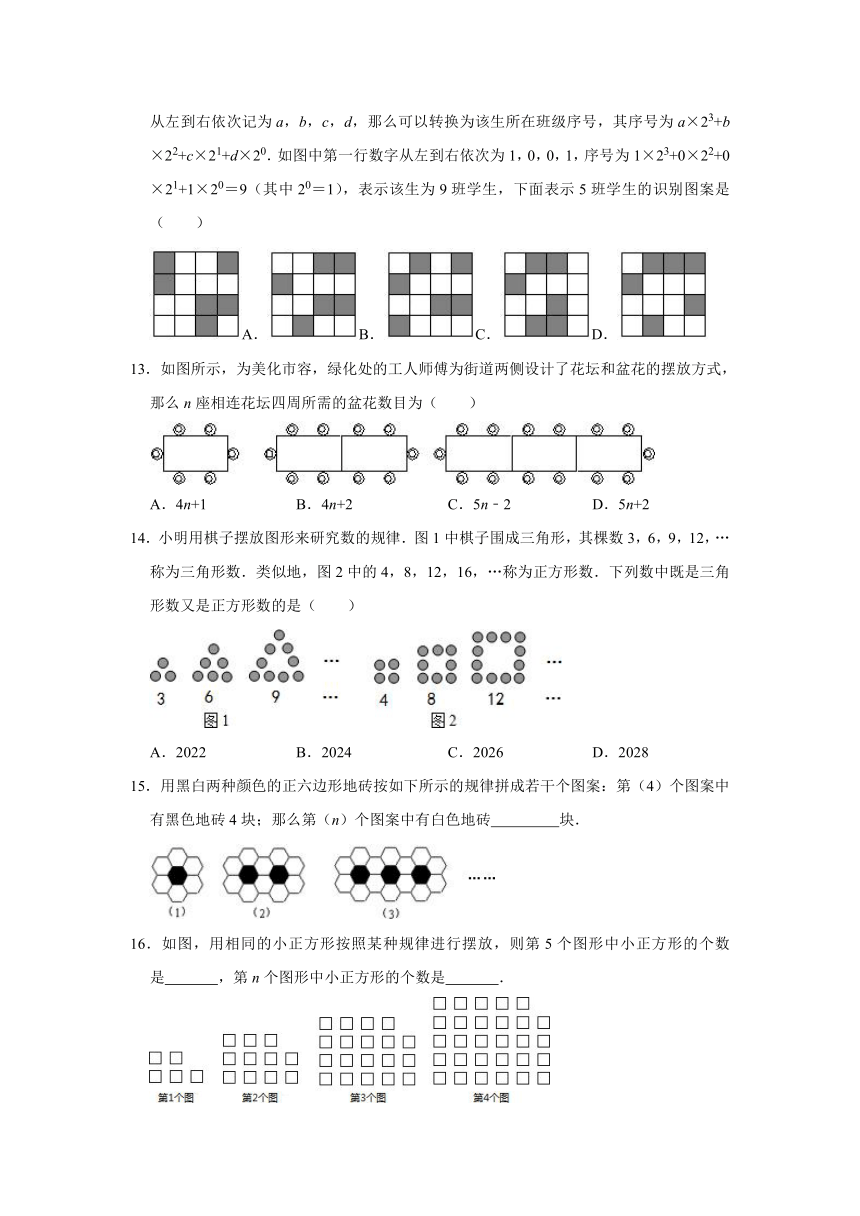
12.在“互联网+”时代,利用二维码可以进行身份识别.某校建立了一个身份识别系统,如图是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20.如图中第一行数字从左到右依次为1,0,0,1,序号为1×23+0×22+0×21+1×20=9(其中20=1),表示该生为9班学生,下面表示5班学生的识别图案是( )
A.B.C.D.
13.如图所示,为美化市容,绿化处的工人师傅为街道两侧设计了花坛和盆花的摆放方式,那么n座相连花坛四周所需的盆花数目为( )
A.4n+1 B.4n+2 C.5n﹣2 D.5n+2
14.小明用棋子摆放图形来研究数的规律.图1中棋子围成三角形,其棵数3,6,9,12,…称为三角形数.类似地,图2中的4,8,12,16,…称为正方形数.下列数中既是三角形数又是正方形数的是( )
A.2022 B.2024 C.2026 D.2028
15.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n)个图案中有白色地砖 块.
16.如图,用相同的小正方形按照某种规律进行摆放,则第5个图形中小正方形的个数是 ,第n个图形中小正方形的个数是 .
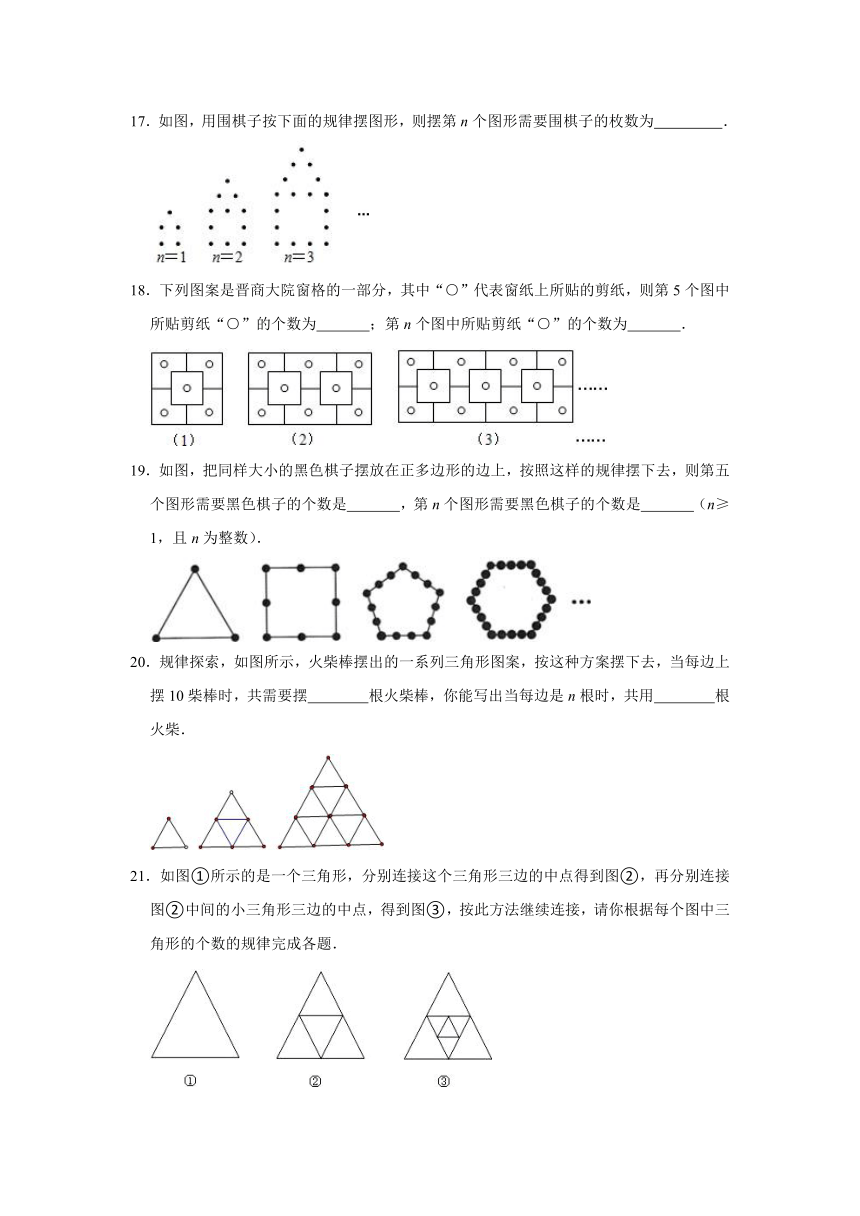
17.如图,用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数为 .
18.下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第5个图中所贴剪纸“○”的个数为 ;第n个图中所贴剪纸“○”的个数为 .
19.如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第五个图形需要黑色棋子的个数是 ,第n个图形需要黑色棋子的个数是 (n≥1,且n为整数).
20.规律探索,如图所示,火柴棒摆出的一系列三角形图案,按这种方案摆下去,当每边上摆10柴棒时,共需要摆 根火柴棒,你能写出当每边是n根时,共用 根火柴.
21.如图①所示的是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间的小三角形三边的中点,得到图③,按此方法继续连接,请你根据每个图中三角形的个数的规律完成各题.
(1)将下表填写完整;
图形编号 ① ② ③ ④ ⑤ …
三角形个数 1 5 …
(2)在第n个图形中有 个三角形;(用含n的式子表示)
(3)按照上述方法,能否得到2013个三角形?如果能,请求出n;如果不能,请简述理由.
参考答案
一.规律型:数字的变化类
1.解:把整数化为分母是2的分数,可以发现该数列中的每一个数的绝对值的分母都为2,分子恰是自然数列的平方,前面的符号,第奇数个为负,第偶数个为正,可用(﹣1)n表示,
故第n个数为:(﹣1)n×,
第8个数为:(﹣1)8×=32.
故答案为:32,(﹣1)n×.
2.解:(1)由题意第8个图的三角形数为×8(8+1)=36,
∴既是三角形数又是正方形数,且大于1的最小正整数为36,
故答案为36.
(2)∵N(n,3)==,
N(n,4)=n2==,
N(n,5)=n2﹣n=,
N(n,6)=2n2﹣n==,
由此推断出N(n,k)=(k≥3).
故答案为:(k≥3).
3.解:(1)由题意知第n行最后一数为n2,则第8行的最后一个数是64,
所以第9行第1个数是65,
所以第9行第7个数是71.
故答案为:71;
(2)由(1)知第n行的最后一数为n2,
则第一个数为:(n﹣1)2+1=n2﹣2n+2,
第n行共有2n﹣1个数;
因为442=1936,452=2025,
2×45﹣1=89,
所以第45行有89个数,最后一个数是2025,
所以2020在第45行,第84个数.
故答案为:45,84.
4.解:观察已知所给式子可知:
分子次数的变化规律是:
2=3×1﹣1;
5=3×2﹣1;
8=3×3﹣1;
11=3×4﹣1;
…、
3n﹣1,
分母的变化规律是:
2=12+1;
5=22+1;
10=32+1;
17=42+1;
…、
n2+1;
符号的变化规律是:(﹣1)n+1,
∴第n个式子是:(﹣1)n+1 .
故答案为:(﹣1)n+1 .
5.解:观察规律第四个等式为:
根据规律,每个等式左侧分母恒为2,分子前两项分别是n+1,n
则第n个等式为:=n
故答案为:,=n
6.解:通过观察各行数发现:每行除去首位两个1外,每个数都是它上方两个数之和(这些数是杨辉三角中除去第一行外的部分).
(1)按此规律,第五行的这列数为:1,5,10,10,5,1.
故答案为:1,5,10,10,5,1.
(2)由第1行所有数的之和为2,第2行所有数的之和为4,第3行所有数的之和为8,第4行所有数的之和为16,可找出第n行所有数的之和为:2n.
故答案为:2n.
7.解:3+1=+=3×1,
8.2+1=+=×,
3+1=+=×,
∵3﹣1=2,3﹣2=1,
41﹣5=36,41﹣36=5,
7﹣2=5,7﹣5=2,
∴一个数为,则另一个数是.
故答案为:.
8.解:由已知得出每行的正整数的个数是1,2,4,8,…,其规律:
1=21﹣1,
2=22﹣1,
4=23﹣1,
8=24﹣1,
…,
由此得出第n行的正整数个数为:2n﹣1.
故答案为:2n﹣1.
9.解:(1)因为第一组数为:12,﹣22,32,﹣42,…,
所以第6个数为:﹣62=﹣36;
故答案为:﹣36;
(2)因为第二组数为:﹣13,23,﹣33,43,…,
所以第n个数为:(﹣1)n n3;
故答案为:(﹣1)n n3;
(3)因为每组数的第10个数分别为:﹣100,1000,﹣200,
所以这三个数的和为:﹣100+1000﹣200=700.
10.解:(1)观察下列单项式:﹣,…按此规律,第5个单项式是x5,第n个单项式是
故答案为:x5,.
(2)n为奇数时,=﹣=b;
n为偶数时,=+=a
故答案为:b或a.
(3)可以这样写一个当n为偶数时值为2,当n为奇数时值为0的式子:
1+(﹣1)n.
故答案为:1+(﹣1)n.
11.解:(1)根据已知规律,第6个分式分母为6和7,分子分别为1和5
故应填:
(2)根据题意,第n个分式分母为n和n+1,分子分别为1和n﹣1
故应填:
证明:=
∴等式成立
二.规律型:图形的变化类
12.解:A.∵a=0,b=0,c=1,d=1.
∴0×23+0×22+1×21+1×20=3,
∴该生为3班学生,
B.∵a=0,b=1,c=0,d=1.
0×23+1×22+0×21+1×20=5,
∴该生为5班学生,
C.∵a=0,b=1,c=1,d=0.
0×23+1×22+1×21+0×20=6,
∴该生为6班学生,
D.∵a=0,b=1,c=1,d=1.
0×23+1×22+1×21+1×20=7,
∴该生为7班学生,
则表示5班学生的识别图案是B,
故选:B.
13.解:2个花坛拼在一起可放2×4+2=10盆,3个花坛拼在一起可放4×3+2=14盆,那么n个花坛拼在一起可放(4n+2)盆;
故选:B.
14.解:∵3,6,9,12,…称为三角形数,
∴三角形数都是3的倍数,
∵4,8,12,16,…称为正方形数,
∴正方形数都是4的倍数,
∴既是三角形数又是正方形数的是12的倍数,
∵2022÷12=168…6,
2024÷12=168…8,
2026÷12=168…10,
2028÷12=169,
∴2028既是三角形数又是正方形数.
故选:D.
15.解:根据图示得:每个图形都比其前一个图形多4个白色地砖,
第1个图里有白色地砖6+4(1﹣1)=6;
第2个图里有白色地砖6+4(2﹣1)=10;
第3个图里有白色地砖6+4(3﹣1)=14;
则第n个图形中有白色地砖6+4(n﹣1)=(4n+2)块;
故答案为:4n+2.
16.解:第1个图形共有小正方形的个数为2×2+1;
第2个图形共有小正方形的个数为3×3+2;
第3个图形共有小正方形的个数为4×4+3;
…;
则第n个图形共有小正方形的个数为(n+1)2+n,
所以第5个图形共有小正方形的个数为:6×6+5=41.
故答案为:41;(n+1)2+n.
17.解:依题意得:(1)摆第1个“小屋子”需要5个点;
摆第2个“小屋子”需要11个点;
摆第3个“小屋子”需要17个点.
当n=n时,需要的点数为(6n﹣1)个.
故答案为6n﹣1.
18.解:第一个图案为3+2=5个窗花;
第二个图案为2×3+2=8个窗花;
第三个图案为3×3+2=11个窗花;
…从而可以探究:
第n个图案所贴窗花数为(3n+2)个,
当n=5时,3n+2=3×5+2=17个.
故答案为:17,3n+2.
19.解:第1个图形是三角形,有3条边,每条边上有2个点,重复了3个点,需要黑色棋子2×3﹣3个,
第2个图形是四边形,有4条边,每条边上有3个点,重复了4个点,需要黑色棋子3×4﹣4个,
第3个图形是五边形,有5条边,每条边上有4个点,重复了5个点,需要黑色棋子4×5﹣5个,
按照这样的规律摆下去,
则第n个图形需要黑色棋子的个数是(n+1)(n+2)﹣(n+2)=n(n+2);
当n=5时,5×(5+2)=35,
故答案为:35,n(n+2).
20.解:当n=1时,需要火柴3×1=3,当n=2时,需要火柴3×(1+2)=9;当n=3时,需要火柴3×(1+2+3)=18,…,
依此类推,第n个图形共需火柴3×(1+2+3+…+n)=,
当n=10时,原式=165.
故答案为:165,.
21.解:(1)图形编号为4的三角形的个数是4×4﹣3=13,图形编号为5的三角形的个数是4×5﹣3=17,
图形编号 1 2 3 4 5 …
三角形个数 1 5 9 13 17 …
(2)图形编号为n的三角形的个数是4n﹣3;
(3)4n﹣3=2013
解得:n=504.
所以能得到2013个三角形,此时n=504.
一.规律型:数字的变化类
1.按一定规律排列的一列数为,2,,8,,18…,则第8个数为 ,第n个数为 .
2.古希腊毕达格拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数,比如:他们研究过图1中的1,3,6,10,….由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…,这样的数为正方形数.
(1)请你写出一个既是三角形数又是正方形数的自然数 .
(2)类似地,我们将k边形数中第n个数记为N(n,k)(k≥3).以下列出了部分k边形数中第n个数的表达式:
三角形数:N(n,3)=n2+n
正方形数:N(n,4)=n2
五边形数:N(n,5)=n2﹣n
六边形数:N(n,6)=2n2﹣n…
根据以上信息,得出N(n,k)= .(用含有n和k的代数式表示)
3.如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
(1)表中第9行第7个数是 ;
(2)2020是表中第 行第 个数.
4.一组按一定规律排列的式子:,…,(a≠0)则第n个式子是 .
5.观察下列各等式:
第一个等式:=1,第二个等式:=2,第三个等式:=3…
根据上述等式反映出的规律直接写出第四个等式为 ;猜想第n个等式(用含n的代数式表示)为 .
6.观察下列按照一定规律写出的各行的数:
第1行:1,1;
第2行:1,2,1;
第3行:1,3,3,1;
第4行:1,4,6,4,1;
….
(1)按照上面的规律写下去,请你写出第5行的这列数 ;
(2)第n行的所有数的和是 (用含n的式子表示).
7.小明在一本书中发现了下面三个奇怪的等式:;;
他一一检验后发现它们都是正确的.小明想除了上述三个之外应该还有这样奇怪的式子,于是小明进一步研究,不但写出了很多这样奇怪的等式,还找到了内在的规律:如果一个数为,另一个数为 时(用a,b表示),可以构成类似上述的奇怪等式.
8.把正整数1,2,3,4,5,…,按如下规律排列:
1
2,3,
4,5,6,7,
8,9,10,11,12,13,14,15,
…
按此规律,可知第n行有 个正整数.
9.仔细观察下列三组数:
第一组:1,﹣4,9,﹣16,25,…
第二组:﹣1,8,﹣27,64,﹣125,…
第三组:﹣2,﹣8,﹣18,﹣32,﹣50,…
(1)第一组的第6个数是 ;
(2)第二组的第n个数是 ;
(3)分别取每一组的第10个数,计算这三个数的和.
10.由于(﹣1)n=,所以我们通常把(﹣1)n称为符号系数.
(1)观察下列单项式:﹣,…按此规律,第5个单项式是 ,第n个单项式是 .
(2)的值为 ;
(3)你根据(2)写出一个当n为偶数时值为2,当n为奇数时值为0的式子 .
11.观察以下等式:
第1个等式:++×=1,
第2个等式:++×=1,
第3个等式:++×=1,
第4个等式:++×=1,
第5个等式:++×=1,
……
按照以上规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第n个等式: (用含n的等式表示),并证明.
二.规律型:图形的变化类
12.在“互联网+”时代,利用二维码可以进行身份识别.某校建立了一个身份识别系统,如图是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20.如图中第一行数字从左到右依次为1,0,0,1,序号为1×23+0×22+0×21+1×20=9(其中20=1),表示该生为9班学生,下面表示5班学生的识别图案是( )
A.B.C.D.
13.如图所示,为美化市容,绿化处的工人师傅为街道两侧设计了花坛和盆花的摆放方式,那么n座相连花坛四周所需的盆花数目为( )
A.4n+1 B.4n+2 C.5n﹣2 D.5n+2
14.小明用棋子摆放图形来研究数的规律.图1中棋子围成三角形,其棵数3,6,9,12,…称为三角形数.类似地,图2中的4,8,12,16,…称为正方形数.下列数中既是三角形数又是正方形数的是( )
A.2022 B.2024 C.2026 D.2028
15.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n)个图案中有白色地砖 块.
16.如图,用相同的小正方形按照某种规律进行摆放,则第5个图形中小正方形的个数是 ,第n个图形中小正方形的个数是 .
17.如图,用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数为 .
18.下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第5个图中所贴剪纸“○”的个数为 ;第n个图中所贴剪纸“○”的个数为 .
19.如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第五个图形需要黑色棋子的个数是 ,第n个图形需要黑色棋子的个数是 (n≥1,且n为整数).
20.规律探索,如图所示,火柴棒摆出的一系列三角形图案,按这种方案摆下去,当每边上摆10柴棒时,共需要摆 根火柴棒,你能写出当每边是n根时,共用 根火柴.
21.如图①所示的是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间的小三角形三边的中点,得到图③,按此方法继续连接,请你根据每个图中三角形的个数的规律完成各题.
(1)将下表填写完整;
图形编号 ① ② ③ ④ ⑤ …
三角形个数 1 5 …
(2)在第n个图形中有 个三角形;(用含n的式子表示)
(3)按照上述方法,能否得到2013个三角形?如果能,请求出n;如果不能,请简述理由.
参考答案
一.规律型:数字的变化类
1.解:把整数化为分母是2的分数,可以发现该数列中的每一个数的绝对值的分母都为2,分子恰是自然数列的平方,前面的符号,第奇数个为负,第偶数个为正,可用(﹣1)n表示,
故第n个数为:(﹣1)n×,
第8个数为:(﹣1)8×=32.
故答案为:32,(﹣1)n×.
2.解:(1)由题意第8个图的三角形数为×8(8+1)=36,
∴既是三角形数又是正方形数,且大于1的最小正整数为36,
故答案为36.
(2)∵N(n,3)==,
N(n,4)=n2==,
N(n,5)=n2﹣n=,
N(n,6)=2n2﹣n==,
由此推断出N(n,k)=(k≥3).
故答案为:(k≥3).
3.解:(1)由题意知第n行最后一数为n2,则第8行的最后一个数是64,
所以第9行第1个数是65,
所以第9行第7个数是71.
故答案为:71;
(2)由(1)知第n行的最后一数为n2,
则第一个数为:(n﹣1)2+1=n2﹣2n+2,
第n行共有2n﹣1个数;
因为442=1936,452=2025,
2×45﹣1=89,
所以第45行有89个数,最后一个数是2025,
所以2020在第45行,第84个数.
故答案为:45,84.
4.解:观察已知所给式子可知:
分子次数的变化规律是:
2=3×1﹣1;
5=3×2﹣1;
8=3×3﹣1;
11=3×4﹣1;
…、
3n﹣1,
分母的变化规律是:
2=12+1;
5=22+1;
10=32+1;
17=42+1;
…、
n2+1;
符号的变化规律是:(﹣1)n+1,
∴第n个式子是:(﹣1)n+1 .
故答案为:(﹣1)n+1 .
5.解:观察规律第四个等式为:
根据规律,每个等式左侧分母恒为2,分子前两项分别是n+1,n
则第n个等式为:=n
故答案为:,=n
6.解:通过观察各行数发现:每行除去首位两个1外,每个数都是它上方两个数之和(这些数是杨辉三角中除去第一行外的部分).
(1)按此规律,第五行的这列数为:1,5,10,10,5,1.
故答案为:1,5,10,10,5,1.
(2)由第1行所有数的之和为2,第2行所有数的之和为4,第3行所有数的之和为8,第4行所有数的之和为16,可找出第n行所有数的之和为:2n.
故答案为:2n.
7.解:3+1=+=3×1,
8.2+1=+=×,
3+1=+=×,
∵3﹣1=2,3﹣2=1,
41﹣5=36,41﹣36=5,
7﹣2=5,7﹣5=2,
∴一个数为,则另一个数是.
故答案为:.
8.解:由已知得出每行的正整数的个数是1,2,4,8,…,其规律:
1=21﹣1,
2=22﹣1,
4=23﹣1,
8=24﹣1,
…,
由此得出第n行的正整数个数为:2n﹣1.
故答案为:2n﹣1.
9.解:(1)因为第一组数为:12,﹣22,32,﹣42,…,
所以第6个数为:﹣62=﹣36;
故答案为:﹣36;
(2)因为第二组数为:﹣13,23,﹣33,43,…,
所以第n个数为:(﹣1)n n3;
故答案为:(﹣1)n n3;
(3)因为每组数的第10个数分别为:﹣100,1000,﹣200,
所以这三个数的和为:﹣100+1000﹣200=700.
10.解:(1)观察下列单项式:﹣,…按此规律,第5个单项式是x5,第n个单项式是
故答案为:x5,.
(2)n为奇数时,=﹣=b;
n为偶数时,=+=a
故答案为:b或a.
(3)可以这样写一个当n为偶数时值为2,当n为奇数时值为0的式子:
1+(﹣1)n.
故答案为:1+(﹣1)n.
11.解:(1)根据已知规律,第6个分式分母为6和7,分子分别为1和5
故应填:
(2)根据题意,第n个分式分母为n和n+1,分子分别为1和n﹣1
故应填:
证明:=
∴等式成立
二.规律型:图形的变化类
12.解:A.∵a=0,b=0,c=1,d=1.
∴0×23+0×22+1×21+1×20=3,
∴该生为3班学生,
B.∵a=0,b=1,c=0,d=1.
0×23+1×22+0×21+1×20=5,
∴该生为5班学生,
C.∵a=0,b=1,c=1,d=0.
0×23+1×22+1×21+0×20=6,
∴该生为6班学生,
D.∵a=0,b=1,c=1,d=1.
0×23+1×22+1×21+1×20=7,
∴该生为7班学生,
则表示5班学生的识别图案是B,
故选:B.
13.解:2个花坛拼在一起可放2×4+2=10盆,3个花坛拼在一起可放4×3+2=14盆,那么n个花坛拼在一起可放(4n+2)盆;
故选:B.
14.解:∵3,6,9,12,…称为三角形数,
∴三角形数都是3的倍数,
∵4,8,12,16,…称为正方形数,
∴正方形数都是4的倍数,
∴既是三角形数又是正方形数的是12的倍数,
∵2022÷12=168…6,
2024÷12=168…8,
2026÷12=168…10,
2028÷12=169,
∴2028既是三角形数又是正方形数.
故选:D.
15.解:根据图示得:每个图形都比其前一个图形多4个白色地砖,
第1个图里有白色地砖6+4(1﹣1)=6;
第2个图里有白色地砖6+4(2﹣1)=10;
第3个图里有白色地砖6+4(3﹣1)=14;
则第n个图形中有白色地砖6+4(n﹣1)=(4n+2)块;
故答案为:4n+2.
16.解:第1个图形共有小正方形的个数为2×2+1;
第2个图形共有小正方形的个数为3×3+2;
第3个图形共有小正方形的个数为4×4+3;
…;
则第n个图形共有小正方形的个数为(n+1)2+n,
所以第5个图形共有小正方形的个数为:6×6+5=41.
故答案为:41;(n+1)2+n.
17.解:依题意得:(1)摆第1个“小屋子”需要5个点;
摆第2个“小屋子”需要11个点;
摆第3个“小屋子”需要17个点.
当n=n时,需要的点数为(6n﹣1)个.
故答案为6n﹣1.
18.解:第一个图案为3+2=5个窗花;
第二个图案为2×3+2=8个窗花;
第三个图案为3×3+2=11个窗花;
…从而可以探究:
第n个图案所贴窗花数为(3n+2)个,
当n=5时,3n+2=3×5+2=17个.
故答案为:17,3n+2.
19.解:第1个图形是三角形,有3条边,每条边上有2个点,重复了3个点,需要黑色棋子2×3﹣3个,
第2个图形是四边形,有4条边,每条边上有3个点,重复了4个点,需要黑色棋子3×4﹣4个,
第3个图形是五边形,有5条边,每条边上有4个点,重复了5个点,需要黑色棋子4×5﹣5个,
按照这样的规律摆下去,
则第n个图形需要黑色棋子的个数是(n+1)(n+2)﹣(n+2)=n(n+2);
当n=5时,5×(5+2)=35,
故答案为:35,n(n+2).
20.解:当n=1时,需要火柴3×1=3,当n=2时,需要火柴3×(1+2)=9;当n=3时,需要火柴3×(1+2+3)=18,…,
依此类推,第n个图形共需火柴3×(1+2+3+…+n)=,
当n=10时,原式=165.
故答案为:165,.
21.解:(1)图形编号为4的三角形的个数是4×4﹣3=13,图形编号为5的三角形的个数是4×5﹣3=17,
图形编号 1 2 3 4 5 …
三角形个数 1 5 9 13 17 …
(2)图形编号为n的三角形的个数是4n﹣3;
(3)4n﹣3=2013
解得:n=504.
所以能得到2013个三角形,此时n=504.
